Download PDF  
文章快速检索  
  高级检索
引用本文
邢誉峰, 梁昆. 梁纵向与横向耦合非线性振动分析[J]. 北京航空航天大学学报, 2015, 41(8): 1359-1366
XING Yufeng, LIANG Kun. Nonlinear vibration analysis of longitudinal-transverse coupled beam[J]. Journal of Beijing University of Aeronautics and Astronsutics, 2015, 41(8): 1359-1366.
梁纵向与横向耦合非线性振动分析
邢誉峰, 梁昆    
北京航空航天大学 固体力学研究所, 北京 100191
收稿日期:2014-09-10; 网络出版日期: 2015-03-03
基金项目：国家自然科学基金(11372021,11172028);高等学校博士学科点专项科研基金(20131102110039).
通讯作者: 邢誉峰(1964-),男,吉林农安人,教授,xingyf@buaa.edu.cn,主要研究方向为结构动力学.
摘要：纵向振动和横向振动耦合是捆绑火箭等结构中的典型振动现象.以Rayleigh梁为研究对象,通过Hamilton变分原理推导了考虑应变二次项的纵向振动与横向振动耦合控制方程,并用有限元方法对该非线性系统的行为进行了模拟.针对线性系统固有振动频率和非线性纵横耦合动态响应情况,把所得结果与NASTRAN结果进行了比较,二者结果吻合,证明了本方法的正确性.在此基础上,借助振动控制方程和模拟结果,讨论了非线性系统频率与模态的时变特性,非线性动态响应频率成分特性,横向振动和纵向振动相互影响以及共振现象等.研究结果为本方法的实际应用提供了理论基础.
关键词： 非线性     纵横耦合     振动     有限元     Rayleigh梁    
Nonlinear vibration analysis of longitudinal-transverse coupled beam
XING Yufeng , LIANG Kun     
Institute of Solid Mechanics, Beijing University of Aeronautics and Astronautics, Beijing 100191, China
Abstract:The coupling phenomenon of longitudinal and transverse vibration is representative in boost rocket. Taking longitudinal and transverse vibration coupling into account by using the second order term of longitudinal strain, the governing differential equations of Rayleigh beam was derived through Hamilton variational principle, and the finite element method was employed to explore the behaviors of this nonlinear coupling system. As for the inherent frequency of the corresponding linear system and the dynamic responses of nonlinear longitudinal and transverse coupling system, the obtained results were in agreement with those of NASTRAN, which validated the correctness of present method and results. According to characteristics of the viberation governing equations and the results of finite element method, the analyses focused on the time-variable property of nonlinear system frequency, the amplitude-frequency characteristic of nonlinear dynamical responses, the mutual effects of the longitudinal and transverse vibration and resonant phenomenon when the combinations of frequencies of exciting forces are closer to the frequency of the nonlinear system. The results of present study lie the theoretical foundation for the practical application of the present method.
Key words: nonlinear     longitudinal and transverse coupling     vibration     finite element     Rayleigh beam    

飞行器结构物理参数的主要特点之一是其具有时变质量.运载火箭除了具有时变质量参数之外,其几何特征是其具有类似细长梁的构形,其柔性特征致使其弹性变形非常重要,无论对载荷分析还是飞行控制皆如此.

邢誉峰等在文献[1, 2]中,对过载火箭结构系统的动力学特性和变质量火箭系统的分析方法进行了研究.值得指出的是,运载火箭尤其是捆绑运载火箭的纵横耦合特性是不可忽略的,这主要是由于火箭具有柔性结构,并且同时存在纵横载荷(如推力和风载等).当弹性变形不再是小变形时,系统将出现强耦合现象,否则也存在弱耦合现象,如推力致使横向刚度降低.基于此,本文开展了相关的研究工作.

1995年,文献[3]使用谐波增量平衡法求解了文献[4, 5]给出的纵横耦合梁的主共振和倍频主共振响应.1999年,文献[6, 7]推导了等效柔性梁结构纵横耦合非线性动力学方程,并分析了自由振动和受迫振动响应特性.2010年,文献[8]推导了梁纵横向耦合振动的非线性单元刚度矩阵,用有限元方法求解了动态响应,并分析了耦合响应中的倍频现象等.文献[9]利用Galerkin法和谐波增量平衡法研究纵向运动梁在纵横耦合情况下的自由振动响应,尤其是在横向第1阶和第2阶固有频率之比接近1∶ 3内共振条件下的系统响应.文献[10]研究了水中塔架等效梁模型的耦合振动.文献[11]用模拟和试验方法研究了纵横耦合振动.有些学者则研究纵向激励对横向振动的影响,如文献[12].

已有文献鲜有研究非线性系统的频率特性和响应频率特性,如频率的时变特性、系统频率和响应频率的关系等.在这种情况下,本文开展了有关工作.除了研究频率特性之外,还考虑了共振现象和横向振动对纵横振动影响的特性等.

1 基本方程

对于均匀Rayleigh梁,如图 1所示，若考虑纵横耦合,其几何关系为[5]

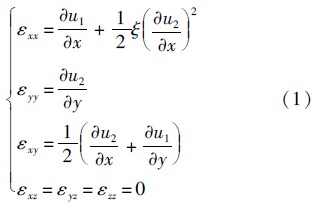
图 1 算例简支梁示意图 Fig. 1 Schematic diagram of simply supported beam example
图选项
式中:ξ为非线性或耦合作用因子,ξ=1对应几何关系的原来形式,ξ=0对应线性系统,其他情况对应作者考虑的其他情况如弱耦合情况等;εij(i,j=x,y,z)为6个应变分量;位移(u1,u2,u3)为与坐标系(x,y,z)对应的位移场函数,其表达式为

式中:w为横向位移;y为厚度坐标;t为时间.将式(2)代入式(1)得

系统应变能函数Uε和动能函数T分别为

式中:L为梁长;E为弹性模量;A为横截面积;ρ为体密度;EI为弯曲刚度;u为梁的纵向位移.

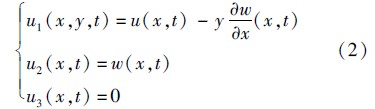
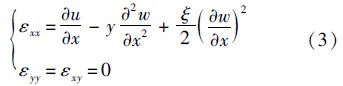
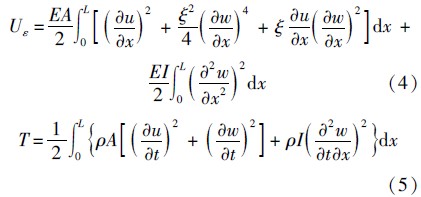
动能函数中忽略了耦合项.根据Hamilton原理得到Rayleigh梁纵横耦合模型振动控制方程

和边界条件,见表 1.式(6)中Fu和Fw为纵向和横向载荷.

表 1 纵横耦合梁边界条件 Table 1 Boundary conditions of longitudinal and transverse coupled beam
表选项

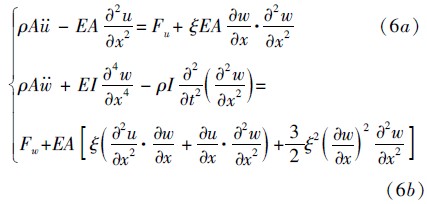
从方程(6),初步得到如下结论:

1) 若考虑非线性纵横耦合,从方程(6a)右端项可以看出,纵向振动中除了包括系统纵向频率和激励频率信息之外,还包括横向振动频率和激励频率的各种组合和倍频.

2) 从方程(6b)右端项可以看出,横向振动中除了包括系统横向频率的各种组合和倍频信息之外,还包括系统纵横各个频率和激励频率的各种组合.

3) 若没有横向激励或横向初始扰动,纵向振动将无法引起横向振动,反之不然.

在下面算例中,还将详细讨论上述结论.

2 有限元求解 2.1 位移函数

下面分别用线性拉格朗日函数和三次埃尔米特函数表达梁的纵向位移u和横向位移场w,其有限元离散形式为[13]

式中:

式中：l为单元的长度.

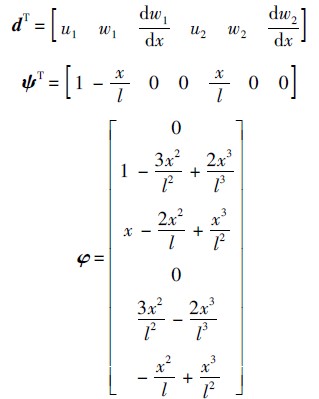
2.2 结构单元矩阵

把位移函数式(7)代入能量泛函,可以得到用结点位移向量表示的应变能函数Uε和动能函数T的标准形式,即

式中单元矩阵为

其中:

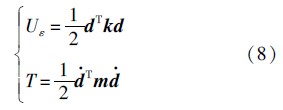
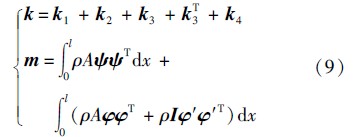
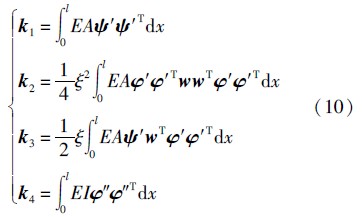
由结构单元矩阵可以看出,单元质量矩阵与不耦合情况下单元质量矩阵相同,这是因为动能函数中没有考虑耦合项,见式(5); k 1和 k 4为通常的等应变杆单元和三次梁单元的刚度矩阵; k 2和 k 3为梁单元纵横耦合刚度矩阵,其元素与振动状态直接相关,即刚度矩阵是时变的.在形成这两个耦合矩阵时,本文利用前一时刻的位移向量来计算当前时刻的刚度矩阵.在本文算例中,针对每个时间步,没有进行迭代.当时间步长较小时,所得结果的精度是可以保证的.

把结构单元组装后,根据变分原理可得系统的离散形式动力学方程:

式中: M 、 K 和 F 分别为结构的总体质量矩阵、刚度矩阵和载荷列向量.

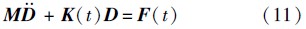
3 数值模拟和分析

这里所用模型的主要参数来自文献[7],表 2给出了几何模型和材料参数、有限元模型参数和边界条件,表 3给出了激励载荷.本文作者用MATLAB[14]自编了动力学响应分析程序,其中用的是Newmark直接积分法.时域范围为0~1s,时间步长h=0.1ms.单元类型是三次梁单元,其纵向变形是线性的,3个结点参数包括纵向位移、横向位移及其导数(斜率).激励作用点和动态响应观测点为图 1的C点,为距左端距离为L/10的结点,见图 1.如果没有特殊说明,非线性影响系数 ξ=1.

表 2 模型参数 Table 2 Model parameters
模型参数数值
几何模型和材料L/m3
外径/m0.1
内径/m0.05
ρ/(kg·m-3)7850
E/GPa210
有限元模型单元数量120
单元属性横向位移为三次埃尔米特函数,纵向位移为线性函数
边界条件纵向
横向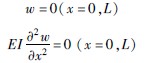
表选项

表 3 激励载荷 Table 3 External forces
激励形式横向纵向
Fwsin(2πfwt)Fusin(2πfut)
Case1fw=6Hz,Fw=20 kNfu=15Hz,Fu=200 kN
Case2fw=0,Fw=0fu=15Hz,Fu=200 kN
表选项
3.1 模型的正确性

为了验证本文工作的正确性,下面把作者自编MATLAB程序的计算结果与NASTRAN结果进行对比.NASTRAN结果中用的是Euler梁单元(不考虑剪切变形和截面转动惯量).为了对比,此处MATLAB质量矩阵中不考虑截面转动量的影响.

表 4给出了横向和纵向前9阶线性系统固有振动频率的比较,二者与理论结果吻合.

表 4 前9阶线性系统固有振动频率比较 Table 4 Comparisons of the first 9 frequencies Hz
阶次横向纵向
理论解本文
结果		NASTRAN理论解本文
结果		NASTRAN

125.312525.312525.3137432.395432.399432.392
2101.250101.250101.2551297.191297.271297.10
3227.812227.812227.8232161.982161.362161.59
4405.000405.000405.0193026.773027.833025.71
5632.812632.812632.8423891.603893.813889.31
6911.249911.250911.2924756.354760.464752.24
71240.311240.311240.375621.145614.365614.36
81620.001620.001620.076485.936480.166475.52
92050.312050.322050.407350.727365.907335.57
表选项

用表 3中Case1给出的激励,不考虑初始条件,图 2给出了两种方法得到的纵横动态响应比较.NASTRAN用非线性瞬态响应分析求解器SOL129;MATLAB用Newmark方法进行计算,二者用相同的时间步长.从图 2可以看出,两种方法响应结果也是吻合的,尤其是横向振动响应.

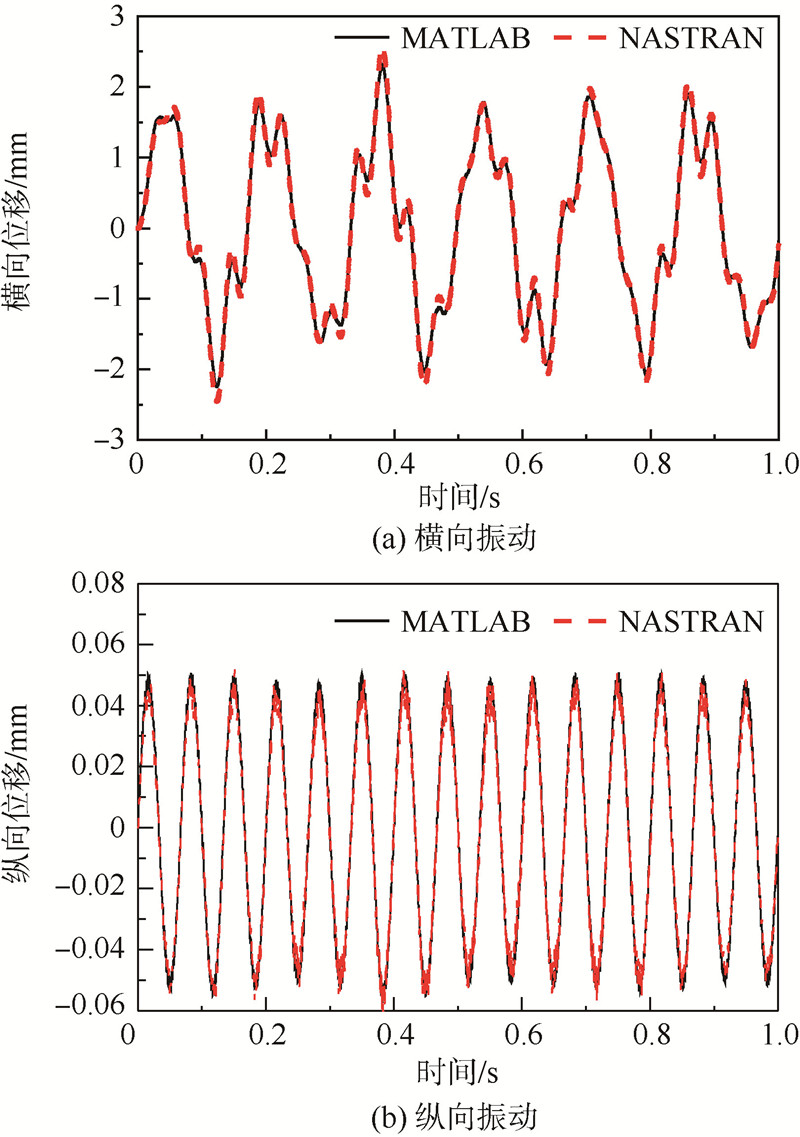图 2 MATLAB与NASTRAN计算的动态响应对比 Fig. 2 Comparison of dynamic responses calculated by

MATLAB and NASTRAN
图选项

通过图 2和表 4的比较可以得到结论,本文推导的公式和程序实现是正确的,为下文对梁的纵横耦合非线性特性的分析奠定了基础.

3.2 耦合系统的频率特性

无论对于梁的线性纵向还是线性横向振动,参见ξ=0时的方程(6),其响应都是由简谐响应叠加而成,其频率成分包括系统的固有振动频率和激励频率.对于非线性控制方程(6),虽然其动态响应特性远比线性系统复杂,但也是由各阶谐波叠加组成,谐波频率成分可以参见在第2节中总结的结论:梁非线性系统动态响应的频率包括系统纵向、横向频率和激励频率的各种组合和倍频.

除此之外,从非线性系统的刚度矩阵子阵 k 2和 k 3可以看出,刚度矩阵是时变的.对于任意微小的时间段,可以假设其频率和模态不随着时间变化,通过式(12)可以求得对应小时间段的频率和模态.

K (t) φ = ω2 M φ (12)

由此可以看出,对于本文研究的几何非线性动力学系统,系统频率是时变的,随着非线性程度降低,其频率成分应该逐渐趋近于对应线性系统的频率,参见图 3,其所用参数与图 2所用参数相同.对于非线性系统,其频率是与响应幅值相关的[15].值得指出的是,对于变系数线性动力学系统,例如变质量系统,系统的频率也是时变的;对于阻尼非线性动力学系统,若阻尼较小,其对频率的影响是可以忽略的,此时可以认为系统频率不是时变的.

图 3 非线性系统频率的时变特性 Fig. 3 Time-variable system frequency characteristics of nonlinear system
图选项

为了进一步考虑非线性系统动态响应频率成分的特性,考虑如下两种情况.

3.2.1 受迫振动频率耦合

系统初始条件为零,激励形式为表 3的Case1,但激励频率更换为fu=17Hz,fw=11Hz.

图 4给出了该受迫振动情况的幅频特性,从中可以看出:

图 4 受迫振动的幅频特性 Fig．4 Amplitude-frequency characteristics of forced vibration
图选项

1) 在纵向幅频特性中,17Hz为纵向激励频率;14Hz和36Hz为横向基频与横向激励频率之代数和(25±11)Hz;22Hz为横向激励频率的2倍(11×2);50Hz为横向基频的2倍(2×25)Hz;5Hz和39Hz分别为横向激励频率的2倍与纵向激励频率之代数和(2×11±17)Hz;19Hz、3Hz和53Hz分别为横向基频与纵横激励频率之代数和(25+11-17、11+17±25)Hz.

2) 在横向幅频特性中,11Hz为横向激励频率;25Hz为横向第1阶固有频率;8Hz和42Hz为横向基频与纵向激励力之代数和(25±17)Hz;6Hz和28Hz为纵横激励频率代数和(17±11)Hz.

3.2.2 自由振动频率耦合

不考虑激励,仅考虑表 5给出的横向初始位移条件,该初始条件是由横向集中力P=4.5422×104N作用在梁上B点得到的,B点距离左端的距离为9L/10.

表 5 横向初始条件 Table 5 Initial conditions of transverse vibration
表选项

图 5给出了幅频特性曲线.横向幅频特性中,主要频率为前4阶系统横向频率,其中并没有包含系统纵 向频率成分,这是由于纵向频率比较高 的缘故.

图 5 自由振动频谱 Fig. 5 Amplitude-frequency characteristics of free vibration
图选项

纵向频谱特性中,50Hz、202Hz、454Hz分别为系统横向频率的二倍频;76Hz、302Hz为横向固有频率的三倍频;126Hz、378Hz为两个横向频率之差;252Hz、430Hz、328Hz、504Hz为两个横向频率之和;600Hz、650Hz为3个横向频率之代数和(228+402±25)Hz.76Hz、126Hz还可以分别表示为前2阶横向频率之差与之和、202Hz还可以表示为第1和第3阶横向频率之差、302Hz还可以表示为第2和第4阶横向频率之差.

3.3 纵横相互影响特征

1) 首先考虑表 3中Case2的激励,初始条件为零.图 6给出了纵横动态响应,从图中可以看出,如果没有横向激励或横向初始条件,纵向振动不能引起横向振动,参见式(6),这是因为此时w′和w″始终为零.若没有纵向激励和纵向初始条件,横向振动却可以引起纵向振动.

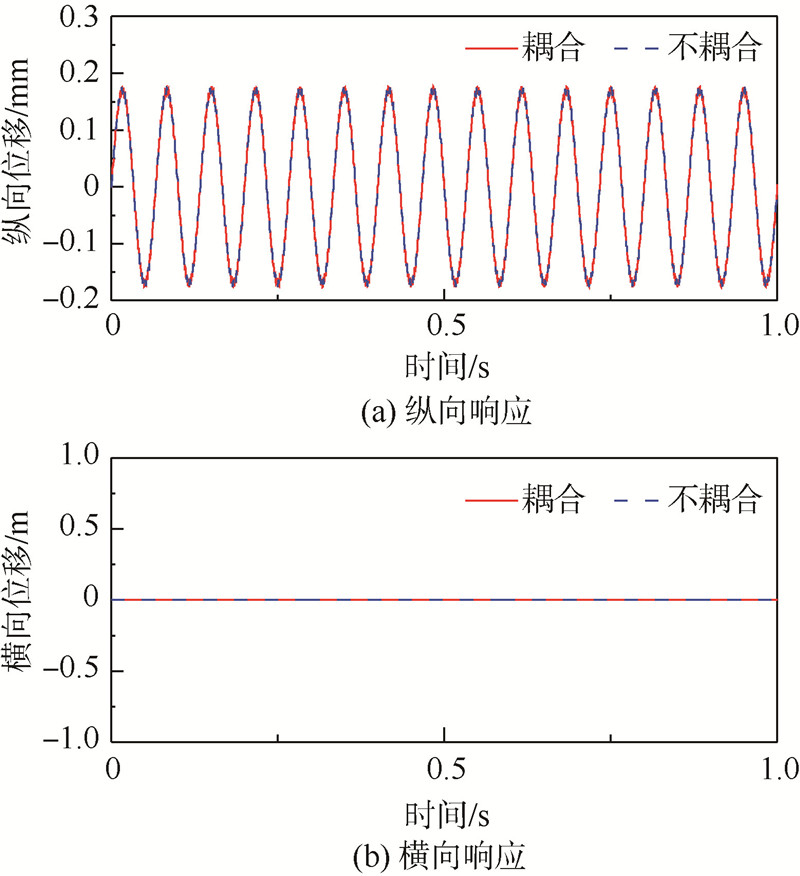图 6 横向初始条件引起的振动响应 Fig. 6 Vibration responses with respect to transverse initial conditions
图选项

2) 考虑表 3中Case1中的横向激励,纵向激励为0,同时考虑表 5给出的横向初始条件.图 7给出了动态响应结果,从图中可以看出,纵向振动对横向振动的影响较小,横向振动对纵向振动的影响比较大.

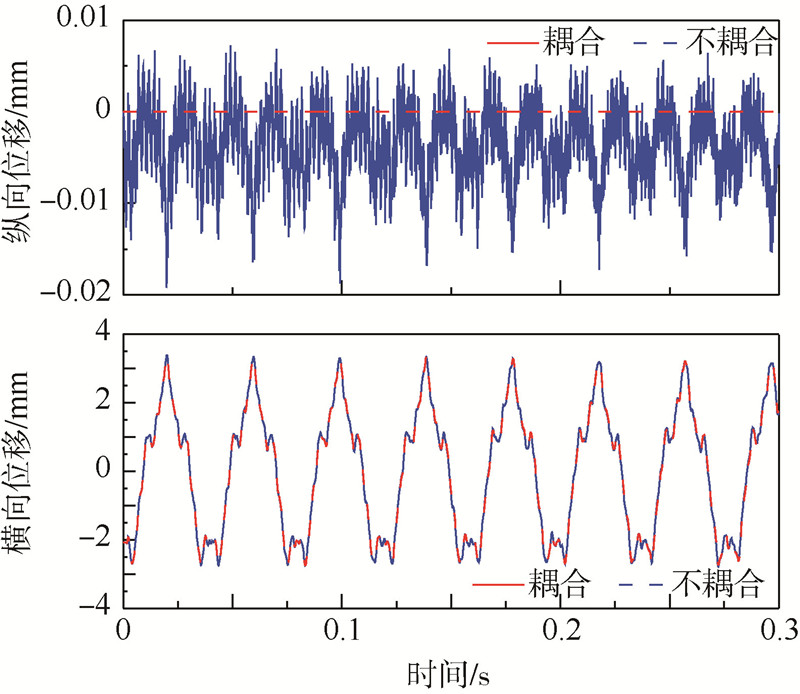图 7 考虑横向初始条件和激励载荷时纵向、横向振动响应 Fig. 7 Vibration response in both longitudinal and transverse directions considering transverse initial condition and excitation force
图选项

3) 横向激励作用下纵向振动响应特性.

纵向激励力为零,不考虑初始条件,分别考虑横向激励力幅值分别为Fw1=20 kN和Fw2=2Fw1作用时纵向动态响应幅值的变化规律,激励频率为11Hz.图 8和表 6给出了分析结果,从中可以看到两种情况下,Fw2作用下的纵向振动幅值基本为Fw1作用下幅值的4倍.从方程(6a)右端第2项可以看出此结论的合理性. 表 6中14Hz近似为

图 8 横向激励载荷幅值加倍后纵向幅频特性 Fig. 8 Longitudinal amplitude-frequency characteristics when transverse excitation forces double
图选项

一阶固有频率与激励频率之差,22Hz激励频率2倍,36Hz近似为一阶固有频率与激励频率之和.

表 6 横向激励载荷加倍时纵向振动幅频特性 Table 6 Longitudinal amplitude-frequency characteristics when transverse excitation forces double
幅频/Hz纵向位移/mm Fw1/Fw2
Fw1Fw2
14(25-11)6.4126.24.08
22(2×11)10.541.63.98
36(25+11)6.4326.44.10

表选项
3.4 共振现象

考虑受迫振动情况,纵向激励频率fu=15Hz,横向激励频率fw=10.3125Hz,二者之和与线性情况横向第1阶固有振动频率相等.

由图 9可知,对于这种情况,非线性横向和纵向振动响应都明显增大.但由于非线性系统频率是时变的,外部激励频率难与非线性系统频率相等,因此也就不会出现因为激励频率与系统固有频率相等且无阻尼时系统幅值为无穷大的情况,这点与线性系统截然不同.

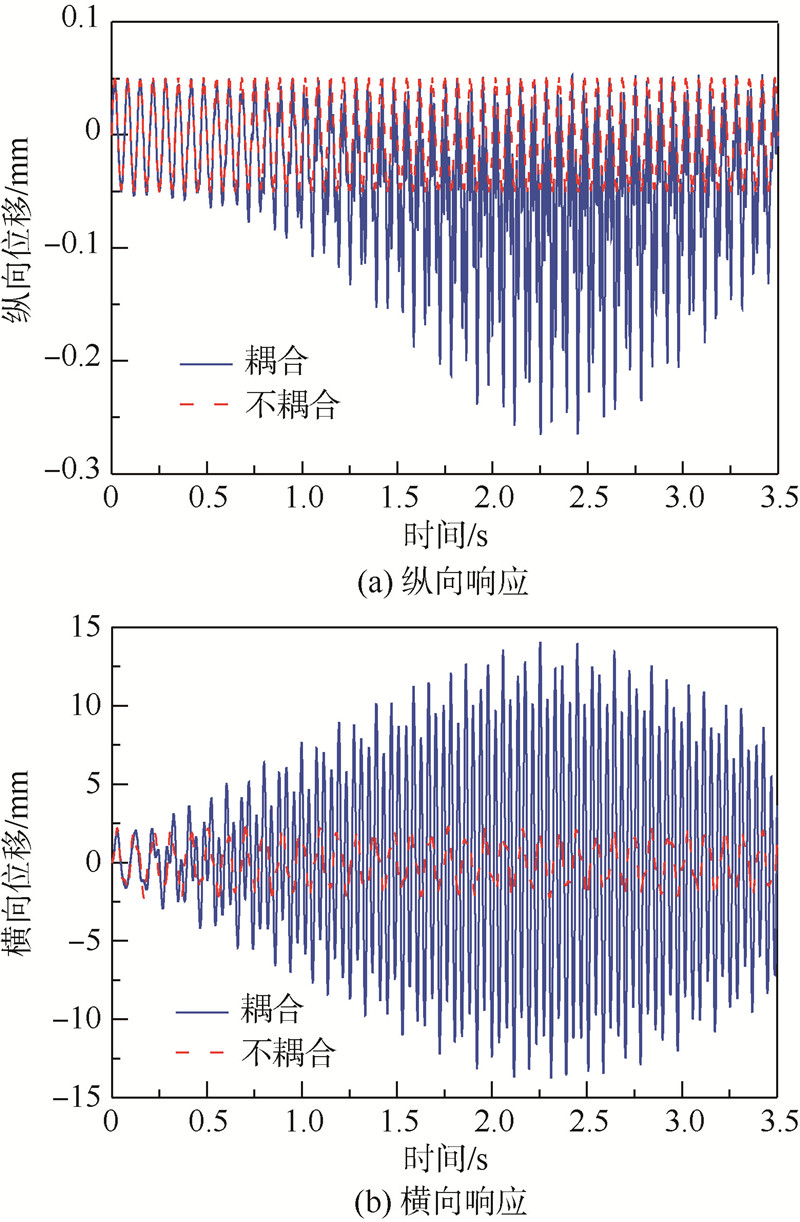图 9 激励频率之和等于横向基频时的振动响应 Fig. 9 Vibration responses when summation of frequency of excitation forces equals to transverse fundamental frequency
图选项
4 结 论

纵向振动与横向振动耦合现象在空间框架和火箭结构中普遍存在,尤其是捆绑运载火箭更是如此.在对此类结构,尤其是对大推力火箭系统,进行力学特性分析时有必要考虑这种耦合现象.通过对控制方程特性和模拟结果的分析比较,得到如下结论:

1) 梁的纵横耦合系统频率是时变的,若非线性程度较小时,其频率趋近对应线性系统的固有振动频率.

2) 梁纵横耦合非线性系统的响应是由各次谐波组成的,各次谐波频率是系统的纵横频率和激励频率的各种代数组合,包括倍频等.

3) 若没有横向激励和横向初始扰动,纵向振动不会引起横向振动.

4) 当激励频率或组合和系统的某阶频率接近时,响应的振幅可能增大,但通常不会像线性系统那样变为无穷大,这是因为激励频率是不变的,而非线性系统频率是时变的,二者难以相等.当纵向激励力明显大于横向激励力时,纵向对横向振动的耦合影响效果会显著增强.

5) 横向激励的幅值增加n倍时,纵向振动幅频特性大约增加n2倍.

参考文献
[1] 邢誉峰,谢珂, 潘忠文.纵向过载环境下变质量欧拉梁动特性分析方法[J].北京航空航天大学学报,2013,39(8):999-1003. Xing Y F,Xie K,Pan Z W.Dynamic analysis methods of variable-mass Euler beam under longitudinal overload[J].Journal of Beijing University of Aeronautics and Astronautics,2013,39(8): 999-1003(in Chinese).
Cited By in Cnki
[2] 邢誉峰,谢珂, 潘忠文.变质量系统振动分析的两种方法[J].北京航空航天大学学报,2013,39(7):858-862. Xing Y F,Xie K,Pan Z W.Two methods for vibration analysis of variable-mass systems[J].Journal of Beijing University of Aeronautics and Astronautics,2013,39(7):858-862(in Chinese).
Cited By in Cnki (3)
[3] 夏品奇, Pun D.纵横向耦合梁的谐波响应分析[J].振动工程学报,1995,8(1):67-72. Xia P Q,Pun D.Harmonic responses of beams with longitudinal and transversal coupling[J].Journal of Vibration Engineering,1995,8(1):67-72(in Chinese).
Cited By in Cnki (13)
[4] 奈弗A H,穆克D T. 非线性振动(上)[M].北京:高等教育出版社,1990:215-242. Nayfeh A H,Mook D T.Nonlinear oscillations volumel 1[M].Beijing:Higher Education Press,1990:215-242(in Chinese).
[5] 奈弗A H, 穆克D T.非线性振动(下)[M].北京:高等教育出版社,1990:93-140. Nayfeh A H,Mook D T.Nonlinear oscillations volume 2[M].Beijing:Higher Education Press,1990:93-140(in Chinese).
[6] Han S M, Benaroya H.Non-linear coupled transverse and axial vibration of a compliant structure,Part 1:Formulation and free vibration[J].Journal of Sound and Vibration,2000,237(5):837-873.
Click to display the text
[7] Han S M, Benaroya H.Non-linear coupled transverse and axial vibration of a compliant structure,Part 2:Forced vibration[J].Journal of Sound and Vibration,2000,237(5):875-900.
Click to display the text
[8] 胡义,杨建国. 梁纵横耦合振动研究[J].武汉理工大学学报:交通科学与工程版,2010,34(3):537-541. Hu Y,Yang J G.Studies on the longitudinal and lateral coupled vibration of beam[J].Journal of Wuhan University of Technology:Transportation Science & Engineering,2010,34(3):537-541(in Chinese).
Cited By in Cnki (5)
[9] 黄建亮,陈树辉. 纵横向耦合轴向运动梁的自由振动响应研究[J].动力学与控制学报,2010,8(4):316-321. Huang J L,Chen S H.Study on vibration of an axially moving beam with coupled transverse and longitudinal motions[J].Journal of Dynamics and Control,2010,8(4):316-321(in Chinese).
Cited By in Cnki (1)
[10] Kuchnicki S N, Benaroya H.Coupled transverse and axial motion of a compliant structure in response to vortex-shedding loads[J].Journal of Sound and Vibration,2002,257(5):903-929.
Click to display the text
[11] Xu X X, Jiao S J,Cheng J L,et al.Study and test of coupled axial and transverse vibrations on drillpipe for rotary drilling rig[J].Applied Mechanics and Materials,2014,472:73-78.
Click to display the text
[12] 张雷,王永. 尾部有推力自由梁的振动分析[J].弹道学报,2010,22(1):83-86. Zhang L,Wang Y.Vibration analysis of free-free beam with end rocket thrust[J].Journal of Ballistics,2014,22(1):83-86(in Chinese).
Cited By in Cnki (3)
[13] 邢誉峰,李敏. 计算固体力学原理与方法[M].北京:北京航空航天大学出版社,2011:51-59. Xing Y F,Li M.The principle and method of computational solid mechanics[M].Beijing:Beihang University Press,2011:51-59(in Chinese).
[14] 徐荣桥. 结构分析有限元法与MATLAB程序设计[M].北京:人民交通出版社,2011:32-40. Xu R Q.Structural analysis and MATLAB program design of the finite element method[M].Beijing:China Communications Press,2006:32-40(in Chinese).
[15] 邢誉峰,李敏. 工程振动基础[M].2版.北京:北京航空航天大学出版社,2011:199-210. Xing Y F,Li M.Foundation of engineering vibration[M].2nd ed.Beijing:Beihang University Press,2011:199-210(in Chinese).
http://dx.doi.org/10.13700/j.bh.1001-5965.2014.0556
北京航空航天大学主办。
0

文章信息

邢誉峰, 梁昆
XING Yufeng, LIANG Kun
梁纵向与横向耦合非线性振动分析
Nonlinear vibration analysis of longitudinal-transverse coupled beam
北京航空航天大学学报, 2015, 41(8): 1359-1366
Journal of Beijing University of Aeronautics and Astronsutics, 2015, 41(8): 1359-1366.
http://dx.doi.org/10.13700/j.bh.1001-5965.2014.0556

文章历史

收稿日期：2014-09-10
网络出版日期: 2015-03-03

相关文章

工作空间