一致性协调策略在解决多智能体协调控制问题上取得了巨大成效与广泛关注,被大量应用于诸如编队、搜索和集结等多种问题[1, 2].一致性协调策略利用局部通信的方式实现多智能体对某个协调变量的共识,也被称为趋同控制.
一致性问题的早期研究热点主要集中在解决含有多种通信约束条件和各类系统模型限制的一致性实现问题上.近年来,为解决多智能体一致性控制渐近稳定收敛时间过长的问题,有学者开始研究减少一致性的收敛时间的方法.作为衡量控制系统性能的重要指标,系统收敛时间不仅在理论研究中具有重要价值,在工程应用中也有重要意义.
学者们首先提出了实现有限时间一致性的方法.其中,Li等通过设计输入下限来约束收敛速度(Lyapunov函数导数)避免渐进特性[3, 4].Masood和Nersesov等提出了基于滑模的控制方法,设计约束保证系统动态在有限时间抵达滑模面[5].这些方法虽然在某种程度上实现了加速,但仍无法保证收敛时间的最优性.
学者们又进一步将注意力转移到最短时间一致性问题上,不仅可以使系统在有限时间内实现稳定,而且保证这个时间的最优性.其中,Xiao和Boyd首先将这一问题描述为与通信拓扑图的邻接矩阵相关的凸优化问题,利用内点法和次梯度优化方法求解这一半正定规划问题,并保证系统在n步(n为智能体个数)内实现收敛[6].在这种优化思想启发下,Chen和Zhang给出一种利用状态预测值作为协调控制增量的办法实现进一步加速[7].但其中控制增量的增益需要人工设置以保证收敛速度比原系统更快.由于同期基于组合图论的方法缺少解析的数学描述工具,仍局限于优化通信拓扑边的权值,其结果劣于Xiao和Boyd[6]的结果.随着组合图论在该领域的深入,学者们基于连通通信拓扑的拉普拉斯矩阵含有全1特征向量的性质,提出了利用最小多项式原理进行设计的方法.其中,Hendrickx等在不改变拓扑结构的情况下,不断修正通信拓扑边的权值使得D+1步(D为通信拓扑直径)时的迭代转移矩阵积为全一矩阵,实现所有状态一致.这意味着将算法迭代步数进一步缩减到D+1[8].不过,文献[6, 7, 8]提出的算法执行过程中需要利用拓扑结构进行全局优化.而Shreyas设计了分散化算法,利用分布式一致性协调控制下线性系统收敛状态可观的特性,智能体可以根据个体D次迭代的状态,在有限步内实现对一致性收敛状态的估计[9].Yuan等进一步优化这一方法.最终保证在分布式协调下局部收敛步数限制在2D+2[10].
就目前对最短时间一致性的研究内容而言,现有文献主要针对输入非受限多智能体系统展开研究.最终收敛状态通常为各智能体初始状态的加权平均[11],权值取决于具体的通信拓扑结构.这意味着系统收敛状态与系统通信拓扑之间存在耦合,当通信拓扑发生改变时,系统收敛状态随之变化.考虑现实物理运动实体存在系统动态约束和输入限制等情况,系统收敛速度又将受限于每个智能体自身的动态特性.特定的拓扑结构会导致系统间协调状态振荡甚至偏向极端状态,这进一步影响系统收敛速度.此时,文献[7, 8, 9, 10]中算法将失去最优特性.因此,研究输入受限的多智能体最短时间一致性具有重要意义.
本文针对输入受限线性多智能体系统展开研究,提出了一种最短时间一致性分布式协调策略.算法实现了一致性收敛状态只与系统初始状态和动态特性相关,而与通信拓扑解耦.在本文提出的分布式算法中,各个智能体根据自身系统动态特性与初始状态约束,通过连通的通信拓扑进行局部协调,找到状态空间内的某个状态使得所有智能体一致到达该状态的时间最短.随后,根据这一状态与对应的最短时间来设计满足终端状态约束与时间约束的最优控制,最终实现多智能体最短时间一致性.
1 基本假设与数学初步本文考察的多智能体系统由满足如下线性时不变输入受限系统动态的智能体构成:
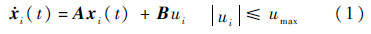
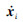 为智能体的状态导数.为描述智能体在任意时间t可到达的状态,引入状态可达区域的概念.
为智能体的状态导数.为描述智能体在任意时间t可到达的状态,引入状态可达区域的概念.
定义1 系统的状态可达区域Ω(t)是指系统从初始状态开始,在可容许输入作用下有限时间t内能够达到的所有状态集合.
引理1[12] 所有满足式(1)系统动态的智能体的状态可达区域Ω(t)为闭、紧且严格凸集,并且对时间t在t>t0上连续,t0为初始时间.
存在容许的控制输入u(t)使得智能体在给定时间t*达到对应状态可达区域Ω(t*)内的任意状态.根据最优控制理论,可知智能体到达该区域Ω(t)边界上状态的控制输入具有bang-bang控制结构,到达该区域Ω(t)内的状态具有bang-off-bang控制结构.
为了描述各个智能体可达区域之间的关系,引入Helly定理.Helly定理[13]是几何学上有关凸集组合相交问题的重要结果之一,被广泛应用解决“加权一中心”等问题.
引理2[14] (Helly定理)给定d维空间上n个凸集C1,C2,…,Cn.如果其中任意d+1个都存在非空交集,那么这n个凸集存在公共非空交集.
文中利用图G(V,E)描述智能体间的通信拓扑,其中:V={1,2,…,n}为顶点集,各顶点代表各个智能体;E⊂V×V为V到V的映射,代表智能体之间的通信链路.对于任意智能体i的邻居集合表示为Ni={j∈V|(i,j)∈E}.假定智能体无主从之分,智能体之间只依赖局部的邻居间通信,通信拓扑满足:
假设1 通信拓扑G(V,E)为双向通信,即
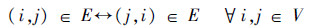

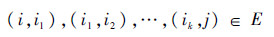
研究多智能体一致性协调控制的目的在于利用少量信息交互实现局部通信限制下的信息(协调变量)共识.在利用这一概念解决诸如集结、搜索和编队等一系列问题的时候,通常选定协调变量为系统状态,控制输入为协调变量间的偏差与偏差导数和[11].这种PID结构的协调策略使得系统协调变量一致收敛为所有智能体初始状态的加权平均值,权值取决于通信拓扑结构与通信权值[11].这种控制方法的收敛速度易受单个个体的牵制而变得缓慢,特别当通信拓扑末端的个体初始状态与系统最终收敛状态偏离较远,其自身驱动能力又较弱时,这种牵制尤为明显.那么,如何通过设计新的协调策略,保证在任意拓扑结构下输入受限系统均以最短时间实现一致性成为本文研究的主要内容.
具体来说,本文研究的问题为如何在假设1的通信条件下,设计分布式协调策略(控制输入)ui,使得所有智能体以最短时间实现状态一致.这一问题可以描述为

导致现有一致性协调策略收敛缓慢的主要原因在于收敛状态初始未知,收敛状态与拓扑相关以及控制律未能考虑系统动态特性等.如果可以通过分布式协调方法预先找到一个状态x*,保证所有智能体同时到达该状态的时间t*少于任意其他状态,随后各个智能体根据x*与t*设计满足自身需求的控制律ui,即可实现最短时间一致性.
具体来讲,通过如下两步解决式(2)描述的问题:
1) 智能体之间通过分布式协调方法找到最短时间一致性状态x*,以及对应系统最短收敛时间t*∈R.
2) 智能体个体根据和来设计满足自身约束的最优控制律,保证各智能体均以t*到达x*.
3.1 集中式算法为了实现上述两步,将首先证明状态x*唯一存在,随后提出一种集中式控制算法,为分布式算法提供一种基本算法.
根据定义1,智能体可达区域Ωi(t)之间的相交区域∩Ωi(t)为所有智能体在t时刻可以共同到达的状态集合,这意味着所有智能体可以以时间t在∩Ωi(t)内实现一致.那么使得Ωi(t)存在公共交集的最小时间t*成为所有智能体出现公共可达状态的最短时间,亦为实现状态一致的最短时间.∩Ωi(t*)为所有最短时间一致性状态集合.可以给出如下最短时间一致性状态与时间的等价定义.
定义2 多智能体{1,2,…,n}的达到一致性的最短时间t*{1,2,…,n}∈R和最终收敛状态x*{1,2,…,n}∈Rd分别为

定理1 对于任意满足系统动态(1)的n个智能体在d维状态空间Rd内实现一致性的最短时间t{1,2,…,n}*与一致性状态x*{1,2,…,n}唯一存在.
证明 首先证明存在性.系统(1)可控,故有
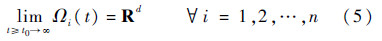
根据引理1,Ωi(t)对t连续,那么必然存在t≥t0,使得
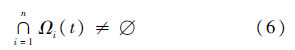
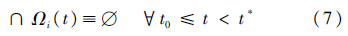
下面证明x*的唯一性.由于Ωi(t)为对t连续的凸集,有限个智能体的∩Ωi(t)也为对t连续的凸集.利用反证法,若∩Ωi(t*)的元素大于1个,则必然存在t*的邻域[t*-δ,t*+δ],其中所有元素均保证∩Ωi(t)≠∅,这与式(7)矛盾.
综上所述,x*与t*唯一存在.
在定理1保证下,可以利用梯度搜索算法对上述最优时间进行求解.搜索的方向根据可达区域是否存在公共交集确定:存在公共交集则向t减少的方向搜索,否则反向.线性系统的可达区域为凸集,可以直接利用交替映射方法(Method of Alternating Projections,MAP)判断可达区域是否存在公共交集[15].对于给定阶次的线性系统而言,可达区域往往可以解析描述,这使交替映射中对点到可达区域的映射获取相对容易.但是,每次的搜索迭代过程中,都需要对每一个智能体的可达区域进行多次映射,因而智能体的数目成为限制搜索速度的重要约束.
在得到时间t*和状态x*后,进入算法的第2步,要求各个智能体依据Pontryagin极大值原理设计含有终端时间t*和终端状态x*约束的最优控制律,保证所有系统以最短时间实现多智能体一致性.由于该一致性状态存在于所有智能体的可达区间内,该最优控制必然有解.
3.2 分布式算法上述集中式方法中对式(6)的判定部分依赖中心节点计算以及完整的信息获取,这违背分布式协调策略只基于邻居间局部交互的假设.因此这一节首先利用Helly定理改善上述集中式算法,使之符合局部协调策略,随后提出一种新的同构式分布式算法.
定理2 对于任意满足系统动态(1)的n个智能体在d维状态空间Rd的最短时间一致性状态仅由该n个智能体中的d+1个决定,即
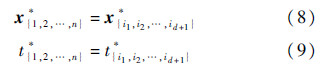
证明 显然,若给定t^使得智能体i与j可以在t实现一致,则对任意t≥t有Ωi(t)∩Ωj(t)≠∅.事实上,假定i与j同构,若令t^时刻后ui≡uj,则t时刻必有xi(t)=xj(t).所以,可达区域Ωi(t)与Ωj(t)之间依然存在交集.这一结论也可以不失一般性地推广到任意多个智能体.
令t*为多智能体系统中任意d+1个的状态可达区域之间存在公共交集的最短时间上界,
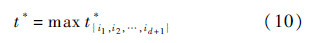
那么根据Helly定理以及Ωi(t)是凸集的性质,可以知道对于d维状态空间内所有Ωi(t)存在公共交集等价于任意d+1个状态可达区域存在交集.则必然有

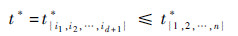
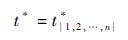

定理2表明,无论智能体数目有多少,实现一致性状态的最短时间只取决于其中的部分“关键”智能体.那么可以将第3.1节的集中式算法中对所有n个智能体的计算减少到某d+1个,求解其一致性状态与实现该状态的最短时间ti,随后选取其中最长时间及对应的状态作为整体一致性状态.这使得共同计算所有n个智能体的情况变得可能,当n>>d时计算量将显著改善.那么借鉴这一思想,每个智能体都对这样d+1个智能体的具体组成与收敛时间进行估计(计算),并向邻居传递自身估计;该个体也会得到邻居传递过来的估计,通过比较自己估计的收敛时间与收到的时间决定是否重新计算.随着每个智能体对这d+1个“关键”智能体的构成实现一致,多智能体系统对最短时间一致性状态达成一致.设计的任意智能体i的局部算法包括:
1) 接收邻居j的j估计,包括j估计的d+1个智能体的编号{j1,j2,…,jd+1}、初始状态以及对应的 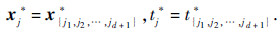
2) 比较tj*与自身估计的收敛时间ti*.如果tj*≤ti*,返回上一步,继续等待接收邻居消息,否则继续执行下一步.
3) 利用j的估计与自身初始状态{i,j1,j2,…,jd+1}重新计算自身估计,得到{i1,i2,…,id+1},xj*=x{i,j1,j2,…,jd+1}*,tj*=t{i,j1,j2,…,jd+1}*.
4) 向邻居传递最新的估计.
各个智能体的初始估计由自身与邻居的初始状态共同计算获得:

算法的停止条件为个体估计在通信拓扑图直径的2倍个周期2D内未发生改变.通常在拓扑图直径未知的情况下,可以令判断周期为2倍的智能体个数.
定理3 在假设1条件下,分布式算法1)~4)步实现各个智能体对最短时间一致性状态x*与时间t*的一致.
证明 因为有限n个智能体中任意的d+1个组合为Cnd+1,所以最多只有Cnd+1个不同的估计.在算法中的步骤2),各个智能体对最短时间一致性时间的估计序列为单调递增序列,因此根据通信拓扑连通性,系统必然在有限时间内对估计达成一致.
又因为任意智能体i的初始估计与算法中步骤3)的更新都引入自身初始状态进行计算,这保证x*i∈Ωi(ti*),所以估计实现一致的时间满足t*≤t{i1,i2,…,in}*.估计得到的d+1个“关键”智能体与定理2所述相同,进而实现了智能体对最短时间一致性状态x*与时间t*的一致.
备注:在分布式算法的证明过程中,仅利用了通信拓扑的双向通信与连同特性,而未对拓扑具体结构形式与通信权值进行要求,所以显然算法得到的结果是与拓扑结构解耦的.
在通过分布式算法协调得到最短时间一致性状态后,各个智能体根据其系统特性与初始状态设计终端时间和终端状态约束下的最优控制律.在定理3的保证下,利用分布式求解算法1)~4)步以及个体最优控制可以解决式(2)描述的多智能体最短时间一致性问题.由于该一致性状态为其中大部分智能体的终端时刻状态可达区域的内点,为包括“关键”智能体在内的其余智能体的状态可达区域边界点,所以最优控制律均可实现.对一致性状态处于其可达区域边界的智能体而言,控制输入为bang-bang控制,切换次数为1次;处于可达区域内点的智能体而言,控制输入可以采用bang-off-bang形式,切换次数为2次.
4 仿真与分析 4.1 仿真设置由于一般高阶线性系统可达区间的获取相对复杂,为了便于理解以及验证算法有效性,本节仅以二阶线性系统为例进行仿真验证.有关系统可达区间的获取办法可以参考文献[16, 17].假定智能体满足二阶动态:
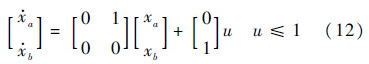
该二阶系统可达区域Ω(t)可以描述为式(13)在相平面xa-xb所包围区域:
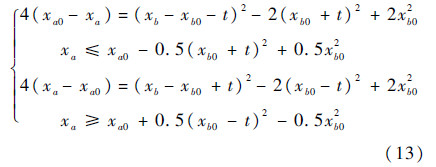
图 1给出的是初始状态为(3,4)的二阶智能体在不同时刻对应的Ω(t).Ω(t)为芒果形凸集区域,随着t的增加而不断增大.
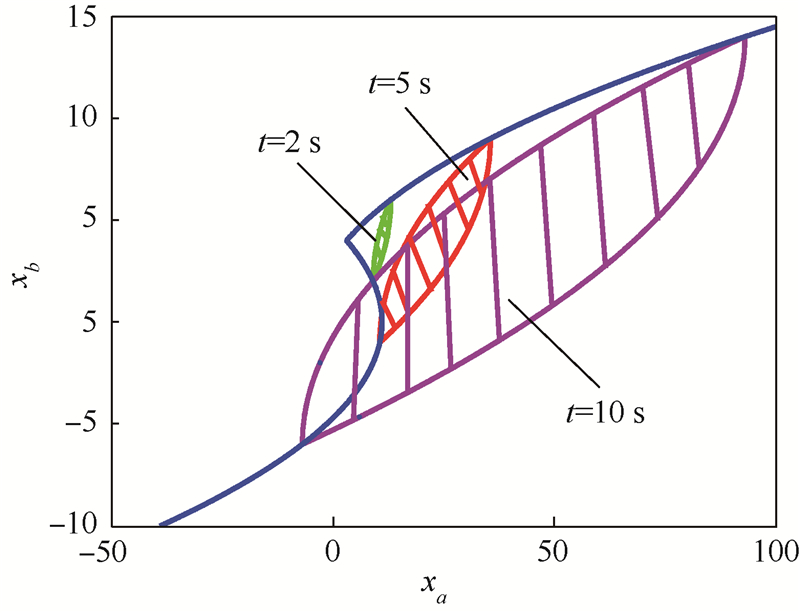 |
| 图 1 二阶系统状态可达区域Ω(2),Ω(5),Ω(10)Fig. 1 State attainable sets Ω(2),Ω(5),Ω(10) of second-order system |
假定存在100(n>2)个智能体,所有智能体的初始状态平均分布在xa∈[1,100],xb∈[0,10]的状态空间内.为了阐述结果与拓扑无关的特性,在相同初始状态下,针对不同通信拓扑进行验证.通信拓扑在满足假设1的条件下随机生成.
4.2 仿真结果与分析根据定理2,由二阶智能体构成的多智能体系统实现最短时间一致性的x{1,2,…,100}*与t{1,2,…,100}*至多由其中的3个“关键”智能体决定.利用本文提出的分布式协调算法,最终得到“关键”智能体为25和26,且x{1,2,…,100}*=(146.07,5.19),t*=18.98 s.仿真结果如图 2所示.
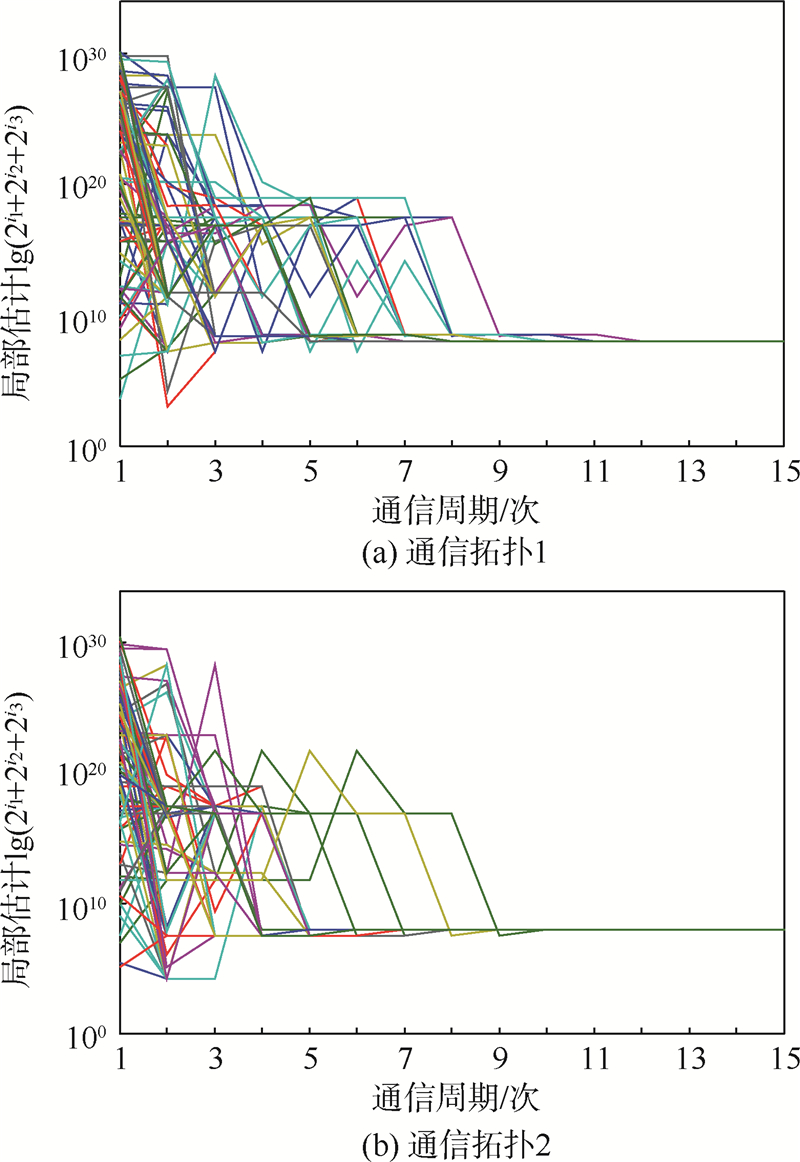 |
| 图 2 不同拓扑下各智能体的局部估计动态过程Fig. 2 Evolution on local guess of critical agents under different communication topologies |
图 2为不同通信拓扑下各智能体的局部估计动态过程,通信拓扑满足平均邻居数为2个,拓扑直径为16.图 2中各曲线代表算法过程中各智能体对“关键”智能体编号{i1,i2,i3}的局部估计变化过程.为了实现在二维图像上绘制所有智能体的局部估计的变化,曲线上各点的纵坐标代表对应智能体估计的“关键”智能体编号{i1,i2,i3}的指数和的对数,即lg(2i1+2i2+2i3).可以看到两个通信拓扑都使得智能体得到相同的最短时间一致性状态.各个智能体对所求的3个智能体分别在迭代12次与10次后达成一致,共同趋于 lg(225+226).
在得到25号和26号为“关键”智能体后,各个智能体即实现x{1,2,…,100}*与t{1,2,…,100}*达成共识.根据协同状态与收敛时间,各个智能体设计满足终端时间和终端状态约束控制律趋向这一状态.根据之前的结论可以知道,这些含状态与终端时间约束的最优解存在并可解.
图 3给出部分智能体在通过局部求解得到的控制输入.可以看出最终收敛状态位于起决定作用的25号和26号智能体的可达区域边界,因此25、26号智能体的控制输入为bang-bang形式,切换次数为1次,而其他智能体一般控制输入为bang-off-bang形式,切换次数为2次.所有控制输入在18.98 s停止.
 |
| 图 3 部分智能体最优控制输入Fig. 3 Optimal control inputs of partly agents |
图 4给出最优控制作用下的部分智能体在相空间内状态变化过程.图中:25号和26号智能体为“关键”智能体(算法结果),20号、30号和70号智能体为随机选择的智能体.
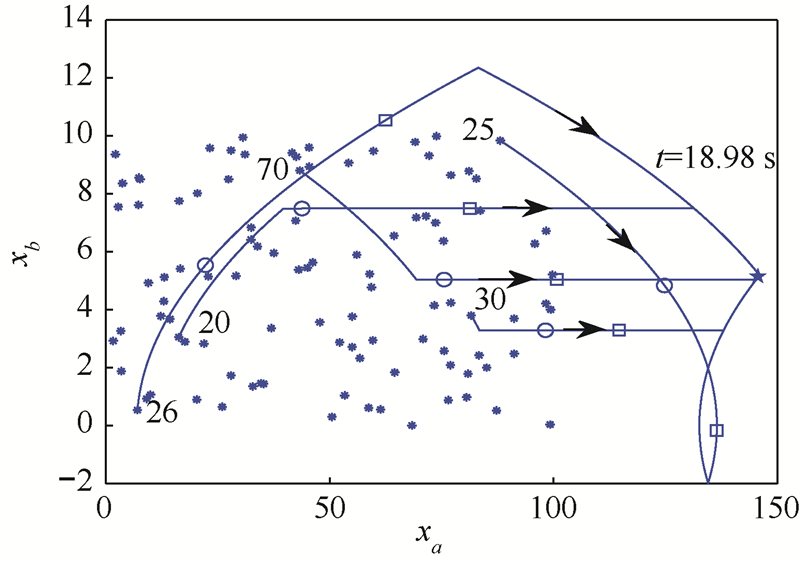 |
 100个智能体的初始状态; 100个智能体的初始状态;
 (146.07,5.19)—多智能体的最短时间一致性状态,
在t=18.98 s共同到达; (146.07,5.19)—多智能体的最短时间一致性状态,
在t=18.98 s共同到达;  —t=5 s时智能体所处状态;
—t=5 s时智能体所处状态;  —t=10 s时智能体所处状态;
—t=10 s时智能体所处状态;  —状态变化方向.
图 4 部分智能体状态在局部最优控制下的相空间运动轨迹Fig. 4 Trajectories of states of partly agents under
local optimal control in state space —状态变化方向.
图 4 部分智能体状态在局部最优控制下的相空间运动轨迹Fig. 4 Trajectories of states of partly agents under
local optimal control in state space |
在提出的分布式最短时间一致性协调方法的驱动下,各个智能体快速地对3个“关键”智能体、最短时间一致性状态和时间达成共识,并最终利用最优控制实现了最短时间一致性.尽管在少于通信拓扑直径数个通信周期内实现了一致性状态的认同,但是每个智能体为了确定与其他所有智能体达成一致,还需要等待额外的2n步完成判断,若能提前知道通信拓扑维度,可以将该额外步数降低到2倍的拓扑图直径.
由于文献[10]只适用于单积分器系统,所以采用文献[10]中模型与数据.在相同的系统输入受限假设下,文献[10]在x=2.682 8实现一致性,需要3.355 s,而本文提出的算法在x=3.688 4实现一致性,只需要2.349 5 s.另外,文献[10]的迭代次数需要2×4=8次,而本文的迭代次数只为3次.事实上,本文算法给出的一致性的最短时间是该问题的下确界.无论选取状态空间中任何其他的状态作为最终的一致性状态,都不可能是最短时间一致性,因为至少有一个智能体到达该状态的时间长于本文算法计算出的结果.
5 结 论1) n个满足线性动态的输入受限多智能体在d维协调状态空间的最短时间一致性状态在Helly定理保证下唯一存在,并只取决于其中的d+1个智能体.
2) 基于上述结论设计的最短时间一致性分布式算法实现了通信拓扑与最终收敛状态的解耦,保证收敛时间最短,避免了由初始状态与通信拓扑导致的收敛时间过长问题.
3) 该算法的理论分析及仿真结果显示,当协调状态维度远小于智能体数量时,所提出的分布式算法计算量明显减少,计算速度显著增加.由于各个智能体采用同构式分布式控制方法,对于额外新增加的智能体可以无缝式扩展,各个智能体分担的计算量不随智能体数量的变化而增加.
| [1] | 闵海波,刘源,王仕成,等.多个体协调控制问题综述[J].自动化学报,2012,38(10):1557-1570.Min H B,Liu Y,Wang S C,et al.An overview on coordination control problem of multi-agent system[J].Acta Automatica Sinica,2012,38(10):1557-1570(in Chinese). |
| Cited By in Cnki (19) | |
| [2] | Cao Y C,Yu W W,Ren W,et al.An overview of recent progress in the study of distributed multi-agent coordination[J].IEEE Transactions on Industrial Informatics,2013,9(1):427-438. |
| Click to display the text | |
| [3] | Li C Y,Qu Z H.Distributed finite-time consensus of nonlinear systems under switching topologies[J].Automatica,2014,50(6):1626-1631. |
| Click to display the text | |
| [4] | Xiao F,Wang L,Chen T W.Finite-time consensus in networks of integrator-like dynamic agents with directional link failure[J].IEEE Transactions on Automation Control,2014,59(3):756-762. |
| Click to display the text | |
| [5] | Masood G,Nersesov S.Finite-time coordination in multiagent systems using sliding mode control approach[J].Automatica,2014,50(4):1209-1216. |
| Click to display the text | |
| [6] | Xiao L,Boyd S.Fast linear iterations for distributed averaging[J].Systems & Control Letters,2004,53(1):75-78. |
| Click to display the text | |
| [7] | Chen Z Y,Zhang H T.Consensus acceleration of multi-agent systems via model prediction[C]//Proceedings of American Control Conference.Piscataway,NJ:IEEE Press,2011:5336-5341. |
| Click to display the text | |
| [8] | Hendrickx M,Raphal M,Jungers O,et al.Graph diameter,eigenvalues,and minimum-time consensus[J].Automatica,2014,50(2):635-640. |
| Click to display the text | |
| [9] | Shreyas S,Hadjicostis C.Finite-time distributed consensus in graphs with timeinvariant topologies[C]//Proceedings of American Control Conference.Piscataway,NJ:IEEE Press,2007:711-716. |
| Click to display the text | |
| [10] | Yuan Y,Stan G,Shi L,et al.Decentralised minimum-time consensus[J].Automatica,2013,49(5):1227-1235. |
| Click to display the text | |
| [11] | Ren W,Beard R.Distributed consensus in multi-vehicle cooperative control:Theory and applications[M].London:Springer,2007:25-27. |
| [12] | Lee E B,Markus L.Foundations of optimal control theory[M].Florida:Krieger Publishing Company,1967:68-80. |
| [13] | Ludwig D,Grünbaum B,Klee V.Helly's theorem and its relatives[J].Proceedings of Symposia in Pure Mathematics in Convexity,1963,VII:101-180. |
| Click to display the text | |
| [14] | Wenger R.Handbook of discrete and computational geometry[M].London:CRC Press,1997:63-82. |
| [15] | Tam K.The method of alternating projections[D].Newcastle: University of Newcastle,2012. |
| Click to display the text | |
| [16] | Varaiya P.Verification of digital and hybrid systems NATO ASI subseries F[M].Berlin:Springer,2000,170:323-331. |
| [17] | Inseok H,Stipanović D,Tomlin C.Advances in control,communication networks,and transportation systems[M].Boston:Birkhäuser,2005:3-19. |



