槽道湍流中应变率张量的拉格朗日时间自相关

doi:10.13700/j.bh.1001-5965.2016.0854

北京航空航天大学学报 ›› 2017, Vol. 43 ›› Issue (12): 2513-2519.doi: 10.13700/j.bh.1001-5965.2016.0854

槽道湍流中应变率张量的拉格朗日时间自相关

鲍赋劼¹, 方乐²

1. 北京航空航天大学能源与动力工程学院, 北京 100083;
2. 北京航空航天大学中法工程师学院, 北京 100083

收稿日期:2016-11-04 修回日期:2017-02-06 出版日期:2017-12-20 发布日期:2017-12-29
通讯作者: 方乐 E-mail:le.fang@buaa.edu.cn
作者简介:鲍赋劼,男,硕士研究生。主要研究方向:槽道湍流;方乐,男,博士,教授,硕士生导师。主要研究方向:湍流理论。
基金资助:
国家自然科学基金（11572025，11202013，51420105008）

Lagrangian time auto-correlation of strain-rate tensor in channel turbulence

BAO Fujie¹, FANG Le²

1. School of Energy and Power Engineering, Beijing University of Aeronautics and Astronautics, Beijing 100083, China;
2. Ecole Centrale de Pékin, Beijing University of Aeronautics and Astronautics, Beijing 100083, China

Received:2016-11-04 Revised:2017-02-06 Online:2017-12-20 Published:2017-12-29
Supported by:
National Natural Science Foundation of China (11572025, 11202013, 51420105008)

摘要/Abstract

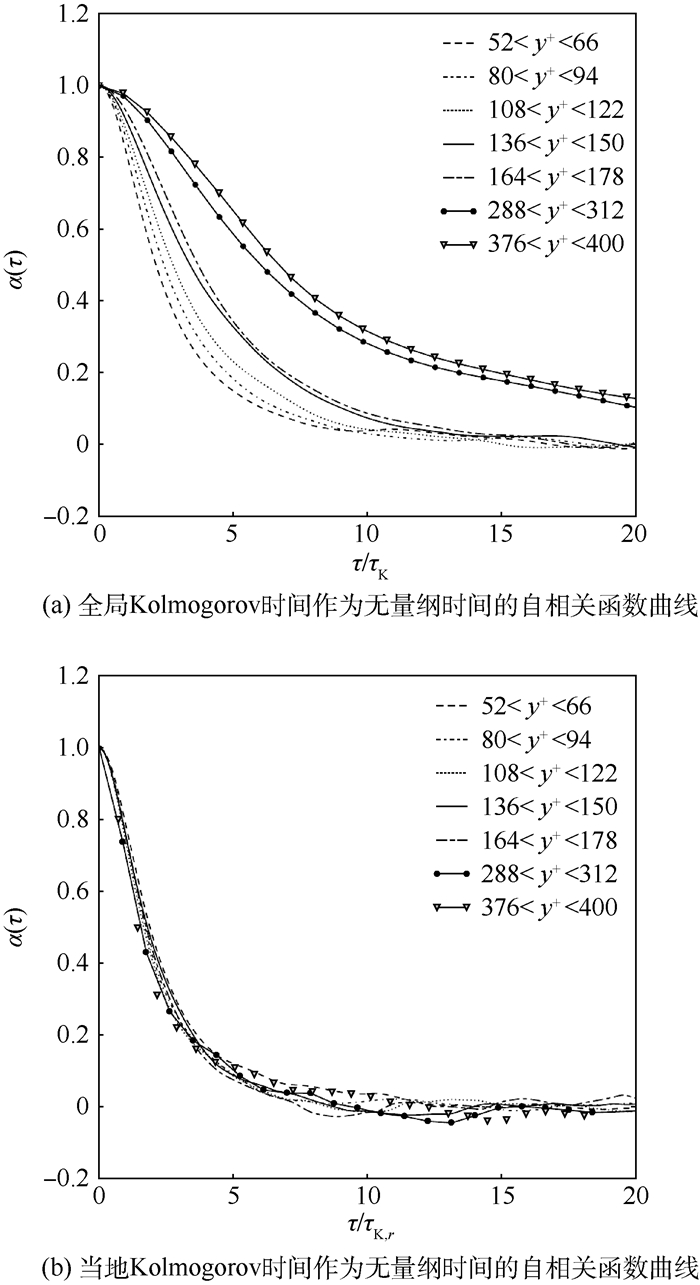
摘要： 已有的研究证实，在均匀各向同性湍流中速度梯度张量（VGT）演化的无量纲时间是当地Kolmogorov时间。本文使用大涡模拟的方法，计算了一个雷诺数7 000的槽道流场，以到壁面的无量纲距离的大小将流场分为不同区间，使用当地Kolmogorov时间对不同区间的应变率张量的拉格朗日时间自相关函数进行无量纲化。发现不同区间自相关函数的下降曲线不完全重合：在对数区中不同区间自相关函数的下降曲线基本重合，但在靠近壁面的黏性底层和过渡层中则无此现象。因此，当地Kolmogorov时间不是槽道中速度梯度张量演化的普适无量纲时间。

关键词: 湍流, 槽道流, 大涡模拟, 应变率张量, 拉格朗日自相关

Abstract: It is confirmed that the dimensionless time for evolution of velocity gradient tensor (VGT) is local Kolmogorov time scale in homogeneous isotropic turbulence. The channel flow at Reynolds number 7 000 was calculated using large-eddy simulation in this paper. The flow field was divided into different regions according to the size of the dimensionless distance to the wall and the auto-correlation functions of different regions were normalized by local Kolmogorov time scale. The decline curves of auto-correlation functions in different regions were found not really the same. In logarithmic layer, the decline curves of auto-correlation functions in different regions almost overlapped, while the similar phenomenon did not exist in viscous bottom layer near the wall and buffer layer. The results show that local Kolmogorov time scale is not the universal dimensionless time of evolution of VGT in channel flow.

Key words: turbulence, channel flow, large-eddy simulation, strain-rate tensor, Lagrangian auto-correlation

中图分类号:

O357.5⁺2

鲍赋劼, 方乐. 槽道湍流中应变率张量的拉格朗日时间自相关[J]. 北京航空航天大学学报, 2017, 43(12): 2513-2519.

BAO Fujie, FANG Le. Lagrangian time auto-correlation of strain-rate tensor in channel turbulence[J]. JOURNAL OF BEIJING UNIVERSITY OF AERONAUTICS AND A, 2017, 43(12): 2513-2519.

参考文献

[1] CHEVILLARD L,MENEVEAU C.Lagrangian dynamics and statistical geometric structure of turbulence[J].Physical Review Letters,2006,97(17):174501.
[2] OOI A,SORIA J,CHONG M S,et al.A study of the evolution and characteristics of the invariants of the velocity-gradient tensor in isotropic turbulence[J].Journal of Fluid Mechanics,1999,381(1):141-174.
[3] ATKINSON C,CHUMAKOV S,BRRMEJO-MORENO I,et al.Lagrangian evolution of the invariant of the velocity gradient tensor in a turbulent boundary layer[J].Physics of Fluids,2012,24(10):677-686.
[4] MENEVEAU C.Lagrangian dynamics and models of the velocity gradient tensor in turbulent flows[J].Annual Review of Fluid Mechanics,2011,43(1):219-245.
[5] KERR R M.Histograms of helicity and strain in numerical turbulence[J].Physical Review Letters,1987,59(7):783-786.
[6] ASHURST W T,KERSTEIN A R,KERR R M,et al.Alignment of vorticity and scalar gradient with the strain rate in simulated Navier-Stokes turbulence[J].Physics of Fluids,1987,30(8):2343-2353.
[7] SREENIVASAN K R,ANTONIA R A.The phenomenology of small-scale turbulence[J].Annual Review of Fluid Mechanics,1997,29(1):435-472.
[8] GIRIMAJI S S,POPE S B.A diffusion model for velocity gradients in turbulence[J].Physics of Fluids A:Fluid Dynamics,1990,2(2):242-256.
[9] MARTIN J,DOPAZO C,VALION L.Dynamics of velocity gradient invariants in turbulence:Restricted Euler and linear diffusion models[J].Physics of Fluids,1998,10(8):2012-2025.
[10] JEONG E,GIRIMAJI S S.Velocity-gradient dynamics in turbulence:Effect of viscosity and forcing[J].Theoretical and Computational Fluid Dynamics,2003,16(6):421-432.
[11] FANG L,BOS W J T,JIN G D.Short-time evolution of Lagrangian velocity gradient correlations in isotropic turbulence[J].Physics of Fluids,2015,27(12):457-472.
[12] FANG L,ZHANG Y J,FANG J,et al.Relation of the fourth-order statistical invariants of velocity gradient tensor in isotropic turbulence[J].Physical Review E,2016,94(2):023114.
[13] YU H,MENEVEAU C.Lagrangian refined Kolmogorov similarity hypothesis for gradient time-evolution in turbulence flows[J].Physical Review Letters,2010,104(8):084502.
[14] TENNEKES H,LUMLEY J.湍流初级教程[M].施红辉,林培锋,金浩哲,译.北京:科学出版社,2015:14-15.TENNEKES H,LUMLEY J.A first course in turbulence[M].SHI H H,LIN P F,JIN H Z,translated.Beijing:Science Press,2015:14-15(in Chinese).
[15] 张兆顺,崔桂香,许春晓.湍流理论与模拟[M].北京:清华大学出版社,2005:11.ZHANG Z S,CUI G X,XU C X.Theory and modeling of turbulence[M].Beijing:Tsinghua University Press,2005:11(in Chinese).
[16] STOLOVITZKY G,KAILASNATH P,SREENIVASAN K R.Kolmogorov's refined similarity hypothesis[J].Physical Review Letters,1992,69(8):1178-1181.
[17] 张兆顺,崔桂香,许春晓.湍流大涡模拟的理论与应用[M].北京:清华大学出版社,2008:101-104.ZHANG Z S,CUI G X,XU C X.Theory and application of large eddy simulation of turbulence[M].Beijing:Tsinghua University Press,2008:101-104(in Chinese).
[18] 周海兵.标量湍流的数值研究[D].北京:清华大学,2003:39-45.ZHOU H B.Numerical research of scalar turbulence[D].Beijing:Tsinghua University,2003:39-45(in Chinese).
[19] XU C X,ZHANG Z S,TOONDER J M J,et al.Origin of high kurtosis levels in the viscous sublayer.Direct numerical simulation and experiment[J].Physics of Fluids,1996,8(7):1938-1944.
[20] FANG L,SHAO L,BERTOGLIO J P,et al.The rapid-slow decomposition of the subgrid flux in inhomogeneous scalar turbulence[J].Journal of Turbulence,2011,12(8):1-23.

槽道湍流中应变率张量的拉格朗日时间自相关

Lagrangian time auto-correlation of strain-rate tensor in channel turbulence

PDF (PC)

可视化

摘要/Abstract

引用本文

使用本文

参考文献

相关文章 15

编辑推荐

Metrics

本文评价

[1]	李彦苏, 张坤, 何承军, 阎超. 低速修正的可压缩求解器对湍流模拟精度的影响[J]. 北京航空航天大学学报, 2019, 45(11): 2199-2206.
[2]	杨慧, 路文睿, 李虹杨, 岳连捷. 基于工程转捩模型的高超声速进气道特性[J]. 北京航空航天大学学报, 2018, 44(7): 1408-1418.
[3]	杜若凡, 阎超, 韩政, 向星皓, 屈峰. DDES延迟函数在超声速底部流动中的性能分析[J]. 北京航空航天大学学报, 2017, 43(8): 1585-1593.
[4]	柏宝红, 李晓东. 翼型湍流尾缘噪声半经验预测公式改进[J]. 北京航空航天大学学报, 2017, 43(1): 86-92.
[5]	杜若凡, 阎超, 罗大海. PANS方法在双圆柱绕流数值模拟中的性能分析[J]. 北京航空航天大学学报, 2015, 41(8): 1374-1380.
[6]	王裕夫, 陶国权, 刘东旭, 武哲. 基于大涡模拟的平流层浮空器气动特性分析[J]. 北京航空航天大学学报, 2015, 41(4): 616-623.
[7]	谢宝林, 邵亮. 基于涡方法生成大涡模拟进口条件的数值计算[J]. 北京航空航天大学学报, 2015, 41(4): 701-706.
[8]	张翔, 阎超. 高超声速热流计算湍流模型性能评估[J]. 北京航空航天大学学报, 2015, 41(2): 337-342.
[9]	王翔宇, 李栋. SST-DES在小分离流动数值模拟中的改进[J]. 北京航空航天大学学报, 2014, 40(9): 1245-1249.
[10]	屈峰, 阎超, 于剑, 陈嘉阳. 高精度激波捕捉格式的性能分析[J]. 北京航空航天大学学报, 2014, 40(8): 1085-1089.
[11]	丛成华, 廖达雄. 阻尼网特性数值模拟[J]. 北京航空航天大学学报, 2014, 40(12): 1691-1696.
[12]	郑玮琳, 阎超. XY-SAS模型中不同网格尺度限制器的影响分析[J]. 北京航空航天大学学报, 2014, 40(12): 1725-1729.
[13]	文晓庆, 柳阳威, 方乐, 陆利蓬. 提高k-ω SST模型对翼型失速特性的模拟能力[J]. 北京航空航天大学学报, 2013, 39(8): 1127-1132.
[14]	刘佳, 阎超, 赵瑞, 蒋海军. DES方法对返回舱气动热环境数值模拟[J]. 北京航空航天大学学报, 2013, 39(5): 590-594.
[15]	高琳, 高歌, 江立军. 用GAO-YONG湍流模式对分离流动的数值模拟[J]. 北京航空航天大学学报, 2013, 39(5): 631-634,639.