Strategy, Model and Numerical Verification for Improving the Success Rate of Enterprise Financing
-
摘要:
造成现代企业融资难的一个常见原因就是投融资双方存在信息不对称, 很容易导致"逆向选择"或引发"道德风险", 因此在一定程度上会成为投融资双方合作的障碍。针对这一现实问题, 提出用合作策略来提高企业融资成功率, 具体措施包括: 通过加强沟通和交流, 在增进彼此信任和了解的基础上, 有效降低投融资双方的信息不对称程度; 当投融资双方对预期收益和存在风险的认知达到一致, 且对利益(合作产生的收益或者成本的减少)分配方案能够达成共识时, 投融资双方理性选择的结果就是更愿意进行合作, 即成功提高了融资交易成功率。此外, 还运用非合作博弈与合作博弈相结合的混合模型, 并结合条件枚举和数值解方法, 对该合作策略的可行性进行了不完全验证。
Abstract:One of the common reasons for the financing difficulties of modern enterprises is that there is information asymmetry between investors and financiers, which can easily lead to "adverse selection" or "moral hazard", so to a certain extent, it will become an obstacle to the cooperation between the two sides. In view of this practical problem, this paper proposes the cooperation strategy to improve the success rate of enterprise financing. The concrete measure is that the information asymmetry between investors and financiers can be effectively reduced by strengthening their communication and exchanges to enhance their mutual trust and understanding. When the two sides reach a consensus on the expected benefits and risks, and agree on the distribution scheme of benefits (i.e., benefits generated by cooperation or reduction in costs), the two sides will make rational choices and are more willing to cooperate, which means that the success rate of financing transactions will be successfully improved. In addition, the feasibility of the cooperation strategy is partially verified by using the mixed model of non-cooperative game and cooperative game, combined with the methods of conditional enumeration and numerical solution. Furthermore, the effectiveness of cooperation strategy proposed in the paper is proved by using the mixed model of non-cooperative game and cooperative game, and the enumeration cases are partially verified by means of the numerical solution method. The results show that cooperative strategy in the process of financing game is beneficial to improving the success rate of enterprise financing.
-
一、 文献综述
世界经济学界普遍认为,企业是否存在稳定的资金来源,或者说企业能否及时筹集到足额的生产要素组合所需要的资金,是企业生存和发展的关键。多年来,经济学学者们运用定性分析及定量分析(借助博弈模型)的方法对大量企业的融资情况进行了深入研究,得出了许多颇具价值的结论,其中较具代表性的研究成果如下:
徐陈杰和杨智勇总结出了中国中小企业融资难的原因,主要包括六点:一是中小企业规模小、综合素质低、抗风险能力弱;二是中小企业财务状况不透明,不利于银行等金融机构的监管;三是中小企业的优质资产中可以用来进行抵押担保的较少;四是银行对中小企业普遍存在“惜贷”现象;五是中国小型金融机构发展不健全,无法满足中小企业的融资需求;六是政府对中小企业的投入相对较少[1]。张安忠提出了化解中小企业融资难的六条措施,即加强中小企业内部治理、银行对不同客户实行不同利率、积极发展中小企业担保机构、加快企业信用等级制度建设、加强银行信贷从业人员道德培养以及推进小微民营银行的发展[2]。林文和高会静通过分析中国企业融资难和融资贵的原因,肯定了中国政府在融资中的作用,并在总结日本、德国和印度三国经验的基础上,提出了完善融资制度、建立多层次融资市场体系以及加快征信体系建设的建议[3]。张洁指出,在以银行贷款为主体的大背景下,中小企业缺少抵押不符合银行贷款要求和贷款规模小的现状,致使银行等监管单位的监管成本高,因此造成中小企业融资难[4]。Stiglitz和Weiss认为,在信息不对称的条件下,信贷市场必然存在逆向选择和道德风险[5]。徐子超认为,信息不对称环境下的信贷配给是中小企业融资难的主要原因,并提出解决信息不对称的思路主要包括:开发关系型信贷业务、发展中小金融机构以及构建中小企业信用担保体系[6]。章娅君通过全面研究中小企业融资难问题,总结出了五个影响最大的原因,即要素市场不利导致经营体制缺陷、产品缺乏竞争力导致收入不足、政府税费负担重侵蚀政策红利、不良产业生态制约战略升级以及资产低效运营误导信用能力[7]。上述文献通过对中小企业融资难的原因进行定性分析,从不同角度提出了解决融资难问题的有效策略和建议。
此外,朱莉斯利用博弈理论对中小企业的融资问题(即企业融资需求与银行之间的动态博弈)进行了均衡分析[8];于翕基于博弈模型分析,提出通过加大对违约的惩罚、加强贷后监管以及进行金融领域改革,可以有效降低融资过程中的信息不对称程度,有利于解决融资难问题[9];韩立岩等基于合作博弈与非合作博弈并存的混合博弈模型,利用Shapley值数据,验证了参与合作企业收益均衡分配的合理性[10];Rogna则论述了效用可转移条件下,博弈模型解的概念和讨价还价模型解的计算[11]。上述文献主要借助博弈模型,对成本或收益分配问题进行分析和求解,然而却均未明确涉及信息不对称与融资成功率的关系问题。因此,笔者拟提出融资过程中合作共赢,即基于合作思想通过减少信息不对称有利于提高融资成功率的策略,并运用非合作博弈与合作博弈相结合的混合模型对策略的正确性加以证明,且进一步对于无解析解的典型事例,给出具体的数值解计算方法。
二、 投融资交易过程中存在的信息不对称
一些学者把影响企业融资的因素分为外部因素和内部因素。外部因素主要包括两类:一是宏观政策层面的因素,如国家相关政策、产业发展规划等;二是投资方因素,如金融行业管理规定以及投资方的风险偏好、抵押或担保要求等。内部因素则主要包括企业自身的财务状况、偿债能力和信用评级等。
(一) 信息不对称及其集合描述
在影响企业融资的众多因素中,信息不对称是一个很重要的影响因素。此处的“信息”不仅仅是指与企业相关的数据,更包括那些可能影响到对项目盈利或者发生风险进行准确判断的关键知识、模型和经验等。信息不对称是指投融资双方对上述信息的掌握不对等,结果可能导致双方对投资项目的盈利能力及收益的预期不一致。
在投融资交易活动中,信息优势的一方往往是融资方,因为在对项目盈利预期以及可能存在的风险(如行业发展前景、潜在销售市场和竞争对手情况)以及实施能力(如企业管理水平、真实财务状况、人力资源情况和技术储备)等相关信息的了解和把握上,融资方具有天然的优势;而投资方的优势可能仅在于其对资本市场的了解更多。
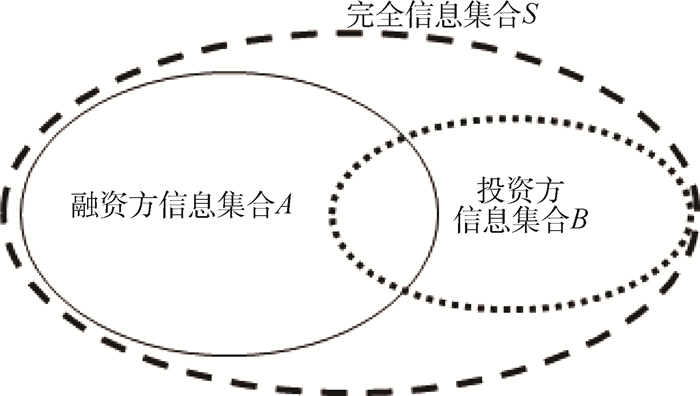
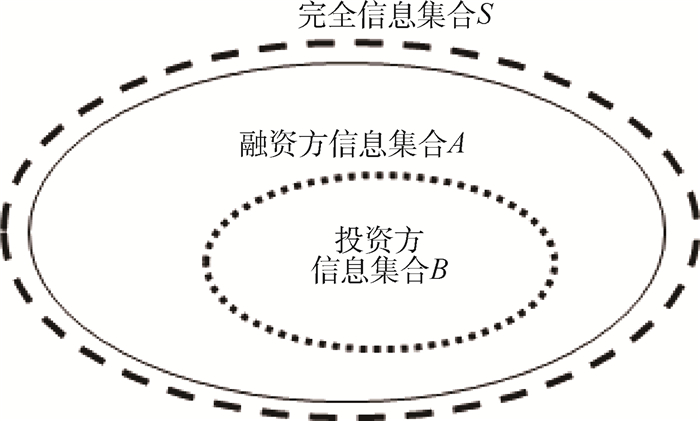
投融资双方的信息集合及信息不对称常表现为两种关系,如图 1和图 2所示。图 1和图 2中:把所有可能影响投融资双方对项目收益和风险进行准确预测的完全信息集合记为S;融资方保有信息集合记为A;投资方保有信息集合记为B。则:图 1中,存在S=A,B⊂A,表明投资方掌握充分的信息,而投资方的信息集合是融资方信息集合的完全子集,此时融资方属于绝对信息优势一方;图 2中,存在A⊂S,B⊂S,且A∩B≠, A≠B, 即信息集合A和B均是完全信息集合S的完全子集,但信息集合A中包含的元素个数远多于信息集合B中包含的元素个数,此时融资方属于相对信息优势一方。
(二) 信息不对称的客观性和绝对性
投融资双方之间信息不对称既然有其存在的客观性,那么是否可以完全消除呢?理论上,尽管投融资双方都存在消除信息不对称的主观意愿,但是客观上完全消除信息不对称却是不可能的,主要原因有二:一是投融资双方掌握的信息均存在偏差。在通常情况下,投融资双方掌握的信息集合更接近图 2中的情形,即双方保有的信息集合A和B都只是完全信息集合S的一个完全子集,且A≠B。在这种情况下,投融资双方基于各自所掌握的不完全信息对投资项目的整体盈利及风险进行预测,由此推导出的结果彼此之间自然会存在较大差异,并且很可能都与正确值之间存在较大偏差。二是信息传递失真和认识偏差。图 1中的融资方尽管对信息掌握比较全面,且主观上很愿意毫无保留地传递给投资方,但在向投资方传递的过程中,由于沟通方式和内容表述准确性等原因,也可能导致部分信息缺失或失真。再进一步,即使投融资双方获得了完全相同的基础信息数据,但由于专业知识、经验和背景的不同,双方在对信息的认知和解读上也可能存在明显偏差。
因此,各参与方,尤其是有信息优势的一方为了消除信息不对称无论作出多大努力,但由于受各方知识、背景和理解力的影响,在投融资方之间,对项目盈利及风险的认识很难一致,这就决定了投融资双方对合作条件的要求不一致。
鉴于信息不对称的客观性和绝对性,投融资双方对合作谈判过程中的策略选择,基于博弈理论显然更加有效和合理,而不能简单地依靠完全的友好协商来实现利益均分。
三、 信息不对称对企业融资的影响以及改进策略和建议
(一) 信息不对称对企业融资的影响
在企业投融资交易活动中,由于存在信息不对称,如果掌握信息的一方利用信息优势在合作中获取不当利益,则必然会对另一方的利益造成损害。因此,从竞争博弈的角度来说,在选择策略时,投资方作为信息劣势一方倾向通过过分强调信息不对称可能对自身利益造成的损害,在合作中提高要价(如高利息),或者要求在投资协议中增加过度保护条款(如业绩对赌),此类要价很容易使投融资双方在合作谈判时产生分歧;而融资方为了反制投资方的过高要价,在策略上可能会通过隐藏对己方不利的信息(如夸大盈利预期和隐藏项目风险)来吸引对方投资,特别是在极端情况下,在项目运作过程中,融资方还可能利用掌握的经营管理权,违规挪用项目资金,为自己谋取其他利益,从而影响项目正常进行,甚至导致收益缩水。因此,投融资双方之间的信息不对称,一方面,可能使双方在谈判中分歧扩大,影响协议的达成;另一方面,也可能为“逆向选择”或“道德风险”埋下隐患。
(二) 减小信息不对称提高企业融资成功率
在企业投融资交易活动中,尽管融资方具有信息优势,但是在整个资本市场,投资方处于主动地位,融资方则处于相对被动地位。因此,由融资方采取主动措施,通过减小信息不对称,增强投资方的信任,变被动为主动,有助于企业投融资交易活动的达成。
融资方所采取的具体措施主要有以下两个方面:一是以诚实可信与合作共赢为出发点。在主观上,尽可能将自己掌握的全部信息准确传递给对方,避免对方对项目真实情况产生误判。二是提高对项目预判的准确性。在技术上,通过优化各种预测和评价模型,对项目预期盈利和可能存在的风险形成更全面、更准确和更完整的预测,因为当基于可信的数据时,投融资双方更容易对预期达成一致。针对图 1所示情形,融资方可以帮助投资方掌握并理解尽可能多的信息,缩小双方保有信息量的差距(使B→A),从而增强投资方开展合作的信心;针对图 2所示情形,投融资双方应共同努力,加强信息交流和沟通,共享各自保有的信息,通过扩大信息集合A和B,使二者同时接近完全信息集合S。
同时,从投资方的角度来说,只有主动优化融资效率评价模型和融资风险评估模型,且基于优化模型取得更精准的企业效能和项目风险评价指标,才能对项目有更加准确和全面的认识。
因为只有相知才能做到互信,所以,如果投融资双方能主动进行交流,减小信息不对称,就有可能消除负面影响并增强互信;而以互信为基础,就有可能将完全竞争关系转化为合作关系,在投资项目预期风险和收益不变的条件下,使投融资双方收益同时增加,这也意味着融资成功率的提高。
(三) 证明思路
在投融资交易活动中,改善信息不对称,增强双方互信,从本质上来说,有利于减少项目运作过程中的监督环节,从而降低监督成本,增加投融资双方可分享的共同收益;但是,共同收益的增加并不意味着投融资双方各自收益都能够同时增加。因此,利益的合理分配也是决定合作能否进行的重要条件,因为如果分配不合理,仅有一方的收益增加,收益减少的一方必然会退出合作,从而致使合作失败。
笔者假设投融资双方在企业投融资交易活动中,采取非合作博弈达到(混合)纳什均衡,在均衡点投融资双方可分配的平均收益组合为(UNC*, VNC*),并满足UNC*+VNC*=E′,其中:UNC和VNC分别为非合作博弈条件下投资方与融资方享有的收益;UNC*和VNC*则分别为在纳什平衡条件下的相应确定值。而如果双方采取合作博弈,并达成纳什谈判解,则双方可分享的收益组合为(UCO*, VCO*),并存在UCO*+VCO*=E,其中:UCO和VCO分别为合作博弈条件下投资方与融资方享有的收益;UCO*和VCO*则分别为纳什谈判解;E和E′则分别为合作博弈、非合作博弈条件下能够分配的预期总收益。那么,如果同时满足以下条件,即

(1) 
(2) 
(3) 由此表明,双方可以通过合作增加各自的平均收益,此时有利于提高融资成功率。
对于由式(1)~式(3)组成的方程组,求解步骤如下:
首先,构造投融资双方的支付函数分别为

(4) 
(5) 然后,计算式(4)和式(5)各自对应的反函数,分别为

(6) 
(7) 将式(6)和式(7)代入UCO+VCO=E中,得到曲线方程为

(8) 此时,如果坐标轴y1和y2,以及式(8)表示的曲线围成凸的解区域,则通过求max{y1y2}的值为

(9) 对式(9)求导数,并令导数为0,即可获得最佳收益分配组合为(UCO*, VCO*)。按照最佳收益分配组合,在投融资双方之间分配收益,就可以达到提升双方收益水平的目标;而如果项目预期收益和风险不变,则双方势必存在更强烈的合作欲望,意味着融资交易成功率的提高。
四、 博弈模型分析
投融资双方能够达成交易的基础在于对项目有着共同的盈利预期,借助项目投资方希望实现自身财富(资本)的保值和增值,而融资方则希望发展生产和增大企业利润。但是,在项目实际推进过程中,由于人性固有的弱点,在利益面前,融资方有可能为了追求自身利益最大化,挪用合作资金,引发道德风险;而投资方由于信息不对称,在无法准确判断项目收益和风险的情况下,可能会选择收益高的项目进行投资,即存在逆向选择的可能。
鉴于此,笔者运用博弈模型,对投融资双方的策略选择以及收益分配进行分析。
(一) 非合作博弈模型分析
非合作博弈是一种当参与者不可能达成具有约束力的协议时的博弈类型,非合作博弈理论旨在解决策略选择问题,即主要研究参与者在利益相互影响的局势中如何选择决策,从而使自己的收益最大化。
作为参照点,首先计算在非合作博弈条件下,投融资双方的各自收益。假定项目预期总收益为E,并且双方初步商定分配比例如下:投资方为γE;融资方为(1-γ)E,其中,γ为初始约定投资方权益占比,但实际收益会根据双方在合作过程中的表现进行调整,守约则奖,违约则罚。
投融资双方可能采取的策略如下:对于融资方,一是严格按照合同执行,二是为了自身利益最大化。违规挪用部分合作资金用于企业其他项目,此时为融资方带来的额外收益为S,但由于部分资金被挪用,可能会导致项目实际收益不及预期,其中给融资方造成的收益减少为N。对于投资方,一是为防止融资方挪用资金,可能提出增设监督机构,此时需要共同支付成本C,但在监督过程中,如果发现融资方确实存在资金挪用现象,作为惩罚,融资方必须向投资方支付罚款M;二是不要求增设监督机构,因为增设监督机构需要共同支付成本,相应地会减少双方可分配收益,如果投资方判断融资方挪用资金概率不大或者即使挪用资金造成的后果不太严重,也可以不要求增设监督机构。
假定投融资双方进行策略选择时都是理性的,那么,对于融资方,只有当挪用资金后所获得的额外收益可以弥补(大于)由于资金挪用导致己方从项目中分享收益的减少部分,才有可能挪用资金,即要满足公式

(10) 对于投资方,只有当发现融资方挪用资金后的罚款M大于己方付出的监督成本γC时,才会要求设立监督机构,即要满足公式

(11) 一般来说,C相对较为固定,对于预期盈利,满足C≪E,只有当E不及预期且很小时,C与E才具有可比性。
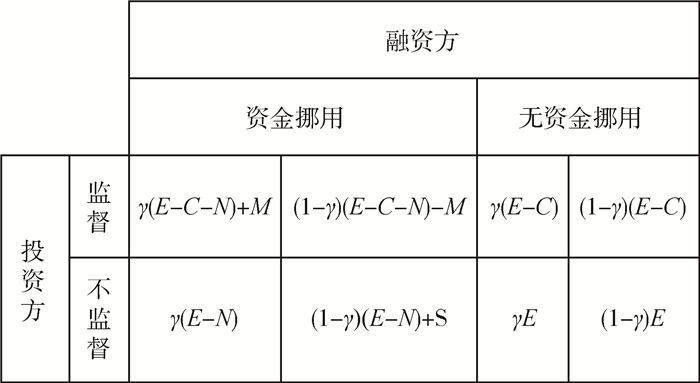
基于不完全信息静态博弈模型,假设融资方挪用资金的概率为p,那么不挪用资金的概率为1-p;同时,投资方提出设立监督机构的概率为q,不提出设立监督机构的概率则为1-q。那么,投融资双方博弈的收益,如图 3所示。
由图 3可知,不存在同时满足双方最大收益的策略对,因此不存在简单纳什均衡。如果计算其混合策略纳什均衡,对于投资方,平均收益为

(12) 对UNC求q的偏导数,由


同理,对于融资方,平均收益为

(13) 对VNC求p的偏导数,由


因此,投资方与融资方在(p*, q*)点处,即

此时:

(14) 
(15) 其中:

(16) 
(17) 由式(10)及式(14)~式(17)得出:A1 < 0和A2 < 0,进一步可得

(18) 
(19) 式(18)和式(19)表明,按照非合作博弈模型,可以找到混合策略纳什均衡,且在均衡状态下,双方获得的总收益小于项目的预期收益。
特别地,当C→0时,A1→0和A2→0,表示如果监督几乎不发生成本,此时投资方与融资方可以按照γ和1-γ的原始比例分享全部总收益E,此时是最理想的状态。
当N→0时,仅有A1→0,表示如果发生资金挪用,但几乎不影响项目盈利,则投资方仍可以按照γ比例分享收益,而融资方可能受到惩罚,因此实际收益会低于预期收益。
当M→∞时,有A1→0和A2→0,表示如果发生资金挪用后,惩罚足够严厉,融资方从理性出发,就不会挪用资金,此时投资方和融资方还是可以按照γ和1-γ的比例分享总收益E。
当S→(1-γ)N时,仅有A2→0,表示如果资金被挪用,且正好抵消掉融资方由于总收益减少而损失的收益,则融资方分享到的收益不变,仍然在总收益中所占的份额为1-γ,但此时投资方收益会减少。
(二) 合作博弈模型分析
合作博弈模型用于研究存在某种有约束力的可执行契约条件下,参与者达成合作时的收益分配问题。对于支付不可转移的二人博弈投融资问题,计算核、核心、核仁和Shapley值等方式获得的解是相同的,其结果就是实现双方之间利益均分,尽管按照上述解进行收益分配很公平,但却未必合理,因为分配结果无法体现对项目执行主体的激励。而按照纳什谈判解进行利益分配,则可以通过定义支付函数来体现对某一方的奖惩,做到公平与奖惩的统一,这样既公平又合理。
纳什谈判解求解方法如下:如果投融资双方采取非合作博弈,在混合策略纳什均衡条件下,投融资方可以获得的平均收益分别是UNC*和VNC*,且UNC*+VNC*=E′,与式(19)比较,可得:E′ < E,当N→0或M→∞时,E′→E。
假定完全竞争博弈转化为合作博弈之后,投资方可以获得额外收益Uad,融资方可以获得额外收益Vad。那么,通过合作,投融资双方可分配到的收益分别为

(20) 
(21) 其中:

(22) 对于支付函数的定义或者选择,可以从三个方面来考虑:一是实际效用角度。对于融资方,假定融资方资产总额为B,融资比例为α,则融资总额为αB(一般地,由于受到风险管控限制,要求负债不能过高,因此,存在0 < α < 1);而对于投资方,一般地,其资产总额会远超B(因为投资方为了降低风险,往往会分散投资,即在单个项目上的投资只占其总资产的很小一部分)。因此,在一般情况下,同样大小的收益(如通过减小信息不对称而获得的额外收益)对融资方的贡献(效用)要大于对投资方的贡献(效用)。二是鼓励主动消除信息不对称。由于融资方属于信息优势一方,因此消除信息不对称的主动权掌握在融资方手中,为鼓励其积极主动消除信息不对称,在分配由于减少信息不对称而获得的额外收益时,适当偏向融资方合情合理。三是体现工作激励。由于在项目推进过程中,融资方担任主要管理职能,其工作态度和工作积极性会直接影响到项目的成败,在分配收益时,随着总收益的增加适度向融资方倾斜以示奖励。
因此,把融资方的支付定义为额外获利的线性函数,同时,把投资方的支付定义为额外获利的对数函数,由于差函数f(x)=x-ln (x)是变量x的单调增函数,这样,可以保证在分配额外获利时,随着项目总收益的增加,融资方可分享到的额外收益总是多于投资方,且增长速度会更快。令投融资双方的支付函数UPAY和VPAY分别为

(23) 
(24) 其中,Uad+Vad=E-E′, 如果不考虑双方的恐吓支付,即认为如果双方不合作,也不可能通过其他合作获得收益,这样,投资和融资双方的纳什谈判解(UCO*,VCO*)可以通过计算max {UPAY VPAY}得到,这样,极值问题的解可以转化为下述方程的解

(25) (三) 合作博弈有利于提高融资成功率
对于投融资问题,在理性前提下,如果投融资双方单纯以自身利益最大化为目标选择策略,按照非合作博弈模型,结果双方可达成的均衡点往往不是各自的最优策略,有时甚至会相差很远。其原因在于:投融资双方为避免劣策略的出现,往往会采取必要的应对措施,导致增加额外成本,从而减少了双方的总体收益;而如果投融资双方能够有效消除信息不对称,增进相互信任,并在此基础上通过订立具有约束力的契约,则可以把纯粹的非合作博弈转化为合作博弈。同时,由于通过合作避免了不必要的附加成本及内部消耗,结果会使投融资双方可以分配的总体收益增加,并按照合作博弈模型分配共同收益,则可以保证双方各自的收益都有所增加,进而增强双方的合作意愿,也就意味着融资成功率增加。
五、 数值解验证
由于式(25)没有解析解,笔者将运用数值解方法,针对某些特定条件下投融资双方分享的收益进行求解,并绘制变化曲线,直观展示投融资双方通过合作博弈可以比非合作博弈分享到更多收益(至少是不少于),这样,在合作项目预期风险和收益均不变的情况下,更多的收益必然促使投融资双方达成合作的意愿更加强烈,表明合作博弈可以在一定程度上提高融资成功率。
(一) 非合作博弈数值解
由式(14)~式(17)可得:













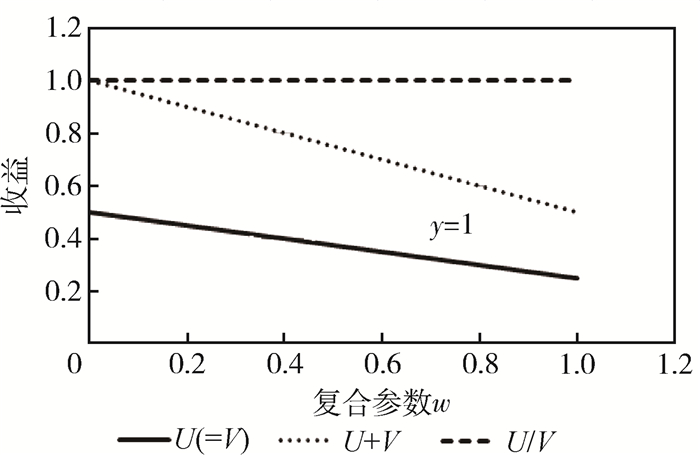
1. 当y=1,即

2. 当y>1(取值

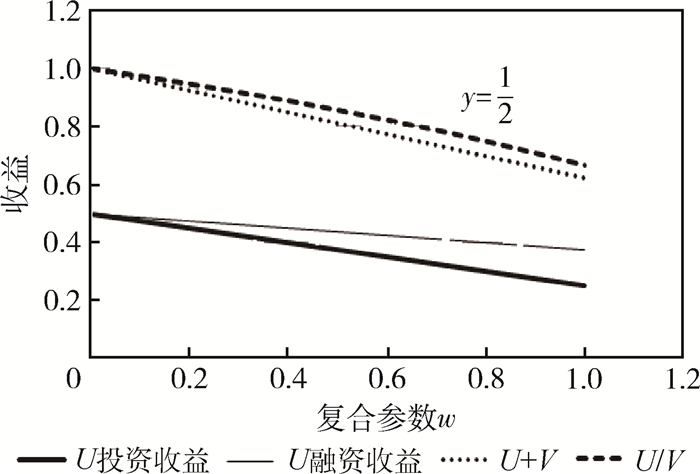
3. 当y < 1(取值

由图 4~图 6可知,







(二) 合作博弈数值解
对于合作博弈,同样以原始均分原则为基础,即令γ=0.5,且E=1,但如果采用简单的利益均分,虽然公平,但不利于调动融资方的积极性。因此,为了充分调动融资方的工作积极性,鼓励融资方通过加强管理增加项目盈利水平,从而实现投融资双方总体可分配利益最大化。
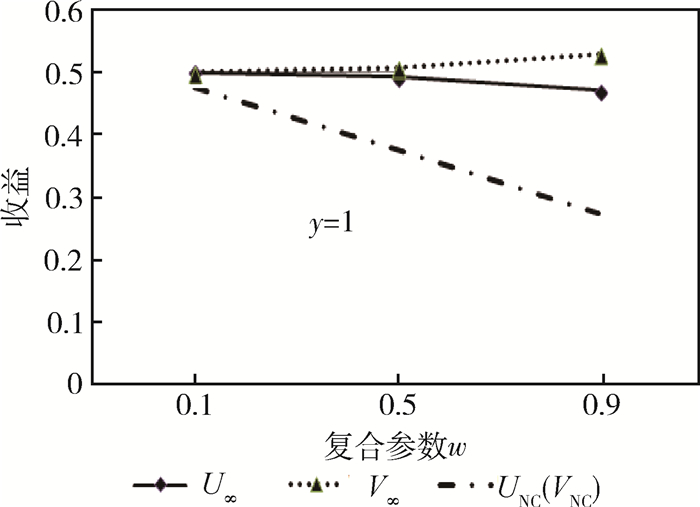
1. 取y=1,且w分别为0.1,0.5和0.9时,UCO*,VCO*(合作博弈)与UNC*,VNC*(合作博弈)的对比值,如图 7所示。
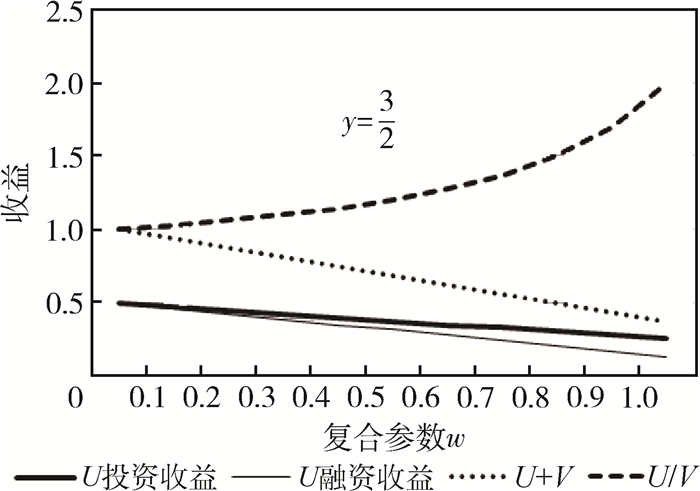
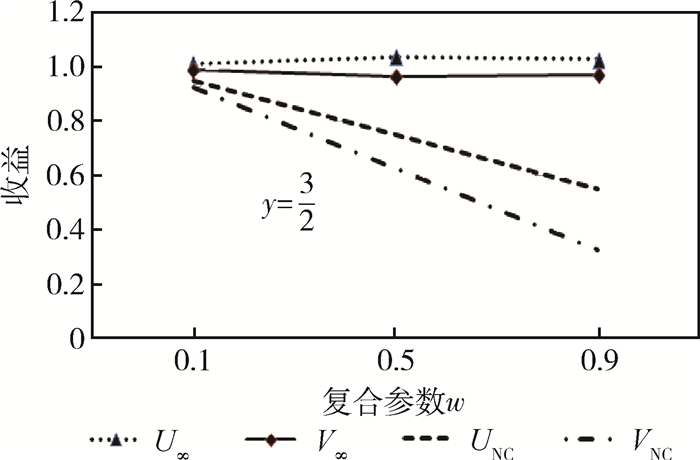
2. 当y>1(取值

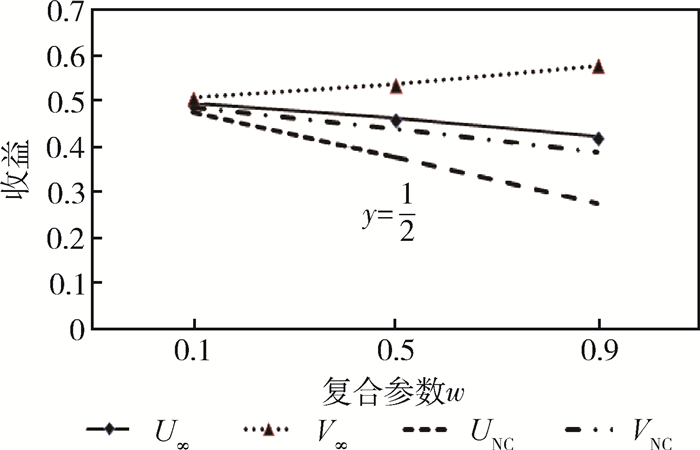
3. 当y < 1(取值

由图 7~图 9可知,在不同y条件下(


另外,由图 8可以看出,如果在非合作博弈均衡点投资方能获得比融资方更多收益,则合作后仍然会比融资方获得更多收益,只是差距会缩小。由图 9可以看出,如果在非合作博弈均衡点投资方比融资方获得较少收益,则合作后获得的收益仍然少于融资方,并且差距会有所扩大。总之,在考虑对融资方激励,分别定义支付函数为对数关系和线性关系条件下,不会改变双方基本的分配关系,但会适当向融资方倾斜。因此,通过改变投融资双方的合作关系,并结合一定激励因素,通过合理定义双方支付函数,就可以达到增加投融资双方收益且维持利益公平分配、提高企业融资成功率的效果。
六、 结论
在企业融资过程中,为了提高企业融资成功率,同时避免出现“逆向选择”和“道德风险”,笔者认为,通过改善双方信息不对称,使投融资双方的关系从竞争走向合作是一个有效策略。
对于上述策略的可行性,笔者运用非合作博弈与合作博弈相结合的模型,基于特定的非合作博弈策略集合,结合特殊的合作博弈效用函数及纳什谈判解,使用条件枚举和数值解方法进行了验证。尽管证明方法还不足够严格和完备,但对于无法获得解析解的问题,使用该方法具有一定的合理性。
-
[1] 徐陈杰, 杨智勇. 金融科技创新缓解小微企业融资难问题探究[J]. 现代审计与会计, 2021(7): 40—41. [2] 张安忠. 金融科技破解小微企业融资难问题及对策[J]. 北方经贸, 2020(2): 98—101. [3] 林文, 高会静. 中小型企业融资难问题研究及探析——以信阳地区为例[J]. 农村经济与科技, 2021, 32(7): 182—183, 240. [4] 张洁. 基于小微企业融资难问题的思考[J]. 黑龙江金融, 2020(2): 63—64. [5] STIGLITZ J E, WEISS A. Credit rationing in markets with imperfect information [J]. American Economic Review, 1981, 71(3): 393—410.
[6] 徐子超. 对解决小微企业融资难问题的思考[J]. 中国集体经济, 2017(16): 63—64. [7] 章娅君. 中小型创业企业融资问题探讨[J]. 管理观察, 2019(1): 50—52. [8] 朱莉斯. 信息不对称下的科技银行与科技型中小企业融资博弈分析[J]. 财会学习, 2020(18): 208—209. [9] 于翕. 我国中小企业投融资的博弈问题研究[J]. 全国流通经济, 2020(36): 98—100. [10] 韩立岩, 甄贞, 王单. 海外投资合作共赢模式的合作博弈分析[J]. 经济与管理研究, 2018, 39(4): 75—84. [11] ROGNA M. Essays in bargaining and cooperative game theory with an application to environmental negotiations [D]. Trento: University of Trento, 2018.
-
期刊类型引用(0)
其他类型引用(5)



 下载:
下载: