一、 问题的提出

近年来，随着社会、政府等对气候异常、环境污染等问题的关注度越来越高，世界各国开始逐步倡导低碳经济，以降低碳排放^[1-2]。碳税政策作为降低碳排放的有效手段之一，目前使用最为广泛。Wissema和Dellink研究了碳税对爱尔兰碳排放的影响，结果表明，征收碳税比只征收能源税能够降低更多的碳排放^[3]；Bjørner 和Jensen分析了能源价格与能源消费之间的关系，结果表明，1993—1997年的碳税制度改革使丹麦的能源消费降低了10%，同时也使碳排放量下降^[4]。上述研究皆认为，征收碳税能够有效降低碳排放，征收碳税是降低碳排放的重要方法之一。

除外部的碳税政策能够促进企业减排外，减排还需要供应链上下游企业的合作，在这样的背景下，供应链的减排问题逐步受到了学术界的普遍关注。Benjaafar等在供应链系统中考虑了碳排放的影响，研究发现，不需额外投入成本，只需控制运营环节就可以显著降低碳排放，同时，供应链企业利用合作可以减少碳排放成本^[5]；Zhao等通过构建博弈模型，分析了企业是否自愿减排对减排决策的影响^[6]；姜跃和韩水华研究了在碳税规制的约束下，供应商参与和零售商成本分担下的供应链减排决策，发现碳税只有在合理范围内才能起到减排作用^[7-8]；赵道致等使用微分博弈的方法，分析得出了碳排放量的运动轨迹^[9]；唐飞和许茂增、杨惠霄和骆建文、魏守道还研究了供应链成员之间的博弈行为对供应链减排的影响^[10-12]。但是，上述关于供应链减排的研究皆是以供应链成员是公平中性为基本假设的，未能考虑供应链成员的公平偏好问题。

行为经济学研究发现，现实中供应链成员在进行决策时并非完全理性，除考虑自身所获得的利润外，还关注利润分配是否公平，即是否具有公平偏好^[13]。现实中，供应链成员会选择拒绝合作来反抗利润分配不公平。例如，由于电子销售渠道给服装品牌“以纯”分配的利润过少，所以“以纯”坚持采用传统渠道进行销售，拒绝电子渠道，这就说明了零售商的公平偏好必然会影响供应链定价等相关决策。目前，已有部分学者将公平偏好引入供应链的研究中：Cui等研究了公平偏好会对供应链运作产生的影响，得出批发价格契约能够有效提高双方收益^[14]；Caliskan-Demirag等以Cui等的研究为基础，进一步分析了市场需求函数为非线性时公平偏好的作用^[15]；王磊等分析了零售商公平偏好如何影响供应链各参与方的博弈行为，发现零售商的公平偏好会使制造商的利润降低^[16]；张克勇等把公平偏好引入闭环供应链中，分析了闭环供应链产品的定价及各参与方的利润如何随公平偏好的变化而变化^[17]。可见，在供应链博弈中，制造商的减排决策同样会受到零售商的公平偏好的影响。

综上所述，笔者拟将零售商的公平偏好引入供应链的减排与定价决策中，分别分析无公平偏好、制造商考虑零售商公平偏好和制造商不考虑零售商公平偏好三种情况下，供应链的减排与定价决策，并分析零售商的公平偏好对供应链减排与定价决策的影响。

二、 问题描述及模型假设

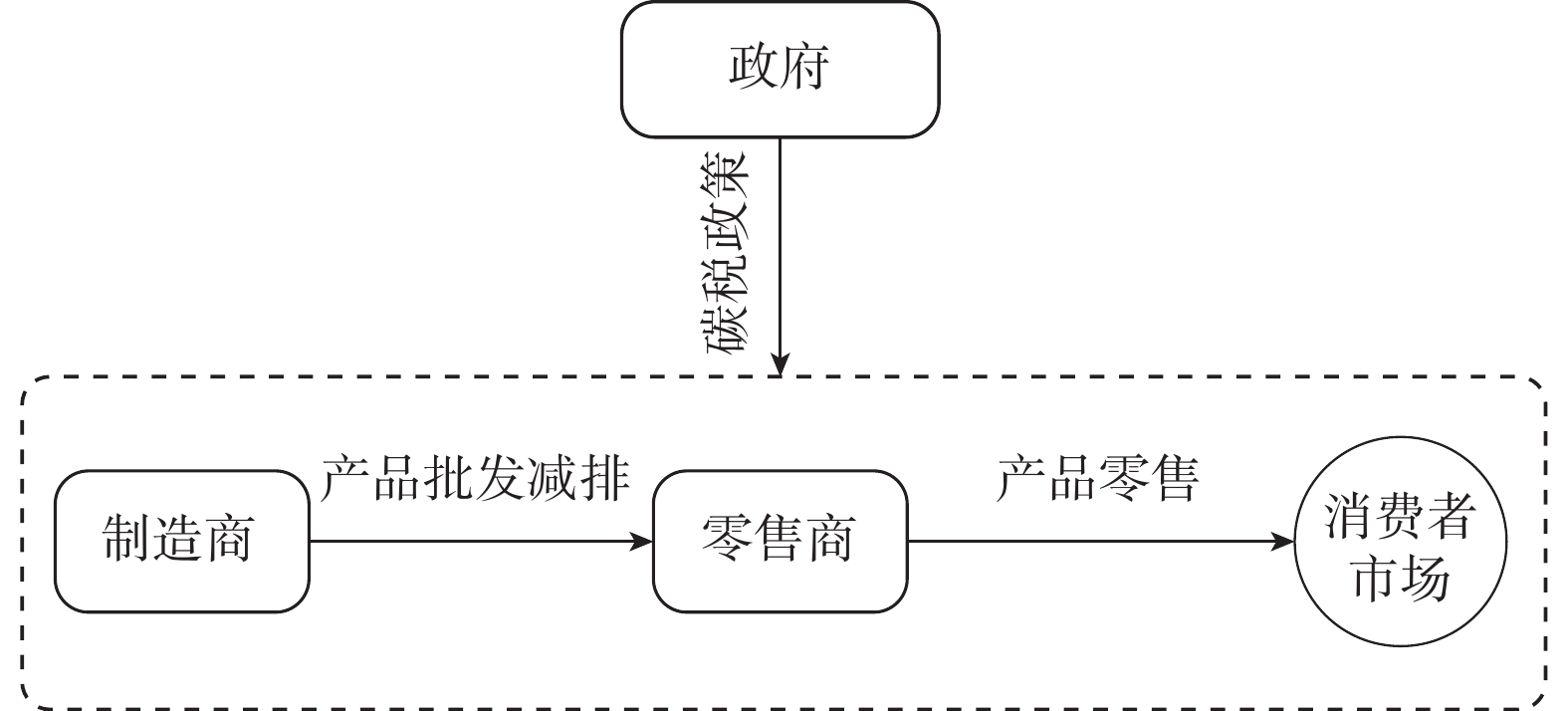
由制造商和零售商组成的低碳供应链结构，如图1所示。零售商首先向制造商批发产品，然后再把产品销售给消费者，政府根据碳排放情况向制造商征收碳税。

图  1  低碳供应链结构

下载: 全尺寸图片 幻灯片

根据研究需要，笔者进行如下设置：

第一，令产品的市场需求函数为D，$ D = a - bp + \delta e $。其中，a为常数，p为产品的零售价格，$ e $为产品的减排量，$ b $为产品的价格敏感系数，$ \delta $为产品的减排敏感系数。在等式的两边同时除以$ \delta $，则原式变为$\dfrac{D}{\delta } = \dfrac{a}{\delta } - \dfrac{{bp}}{\delta } + \dfrac{{\delta e}}{\delta }$，设$D' = \dfrac{D}{\delta }$，$a' = \dfrac{a}{\delta }$，$b' = \dfrac{b}{\delta }$，可得$D' = a' - b'p + e$，与$ D = a - bp + \delta e $特性相同，因此，可令$ \delta = 1 $，则$ D = a - bp + e $。

第二，制造商刚开始减排是相对比较容易的，随着减排量的不断提升，制造商的减排难度越来越大，制造商减排成本函数$ c(e) $满足$ c'(e) > 0 $和$ c''(e) > 0 $，$ k $为减排量对成本的影响系数，则$c(e) = \dfrac{1}{2}k{e^2}$。

第三，政府征收碳税的依据为碳排放量，不考虑特殊行业减征、免征等情况。

第四，令$ {\pi _{\rm{M}}} $为制造商利润，$ {\pi _{\rm{R}}} $为零售商利润，$ {\mu _{\rm{R}}} $为零售商公平效用，$ \boldsymbol{\lambda} $为公平偏好系数。如果零售商具有公平偏好，零售商关注自身与制造商之间的收益对比，因此参照相关研究^[18]，此时零售商的目标函数为$ {\mu _{\rm{R}}} = {\pi _{\rm{R}}} - \lambda \left( {{\pi _{\rm{M}}} - {\pi _{\rm{R}}}} \right) $, 其中$ \lambda \geqslant 0 $。令产品的初始碳排放量为$ \sigma $，碳税为$ t $，产品的批发价格和生产成本分别为$ w $和$ \mathrm{c} $，则可得制造商利润函数为${\pi _{\rm{M}}} = \left( {w - c} \right) \left( {a - bp + e} \right) - \left( {\sigma - e} \right)t - \dfrac{1}{2}k{e^2}$，零售商利润函数${\pi _R} = $ $ \left( {p - w} \right)\left( {a - bp + e} \right) $。

三、 零售商无公平偏好下的减排与定价决策

如果零售商不具有公平偏好，此时利润最大化是制造商和零售商的决策目标。制造商在第一阶段首先确定批发价格和减排量，然后零售商确定零售价格。使用逆向归纳的方法进行求解，首先求出零售价格，其次求出批发价格及减排量。此时零售商的目标函数为

式（1）对p求二阶导数，可得$\dfrac{{{\partial ^2}{\pi _{\rm{R}}}}}{{\partial p}} = - 2b < 0$，所以式（1）存在唯一最优解，令$\dfrac{{\partial {\pi _R}}}{{\partial p}} = 0$，可得产品的最优零售价格为

$ p $分别对$ e $和$ w $求偏导数可得$\dfrac{{\partial p}}{{\partial e}} > 0,\dfrac{{\partial p}}{{\partial w}} > 0$。

据此，可得结论1：当零售商无公平偏好时，零售商所确定的产品零售价格与产品的批发价格正相关，零售商所确定的产品零售价格与制造商的减排量正相关。

结论1表明：零售商应该随着制造商减排量的上升而不断提高产品的零售价格。主要原因在于，制造商提高产品减排量虽然能够提高产品的销量，产品销量的上升能够给零售商带来利润的上涨，但是减排量的上升还会导致产品生产成本的上升，此时制造商会提高产品的批发价格，而批发价格上升给零售商带来的成本的增加幅度大于产品销量上升给零售商带来的利润的增加幅度，所以随着产品减排量的上升，零售商会不断提高产品的零售价格。

接着，制造商根据零售商的决策来确定自身的决策，制造商的决策模型为

将$p = \dfrac{{a + e + bw}}{{2b}}$代入式（3），可得

由于海赛矩阵${\boldsymbol{H}} = \left[ {\begin{array}{*{20}{c}} {\dfrac{{{\partial ^2}{\pi _{\rm{M}}}}}{{\partial {w^2}}}}&{\dfrac{{{\partial ^2}{\pi _{\rm{M}}}}}{{\partial w\partial e}}} \\ {\dfrac{{{\partial ^2}{\pi _{\rm{M}}}}}{{\partial e\partial w}}}&{\dfrac{{{\partial ^2}{\pi _{\rm{M}}}}}{{\partial {e^2}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - b}&{ - \dfrac{1}{2}} \\ { - \dfrac{1}{2}}&{ - k} \end{array}} \right]$，经分析可得，当$bk > \dfrac{1}{4}$，海赛矩阵H为负定的，因此式（4）所表示的制造商目标函数存在最优解，用上标*表示零售商无公平偏好情况下的最优决策，令$\dfrac{{\partial \pi }}{{\partial e}} = 0$，$\dfrac{{\partial \pi }}{{\partial w}} = 0 $，可得

将式（5）代入$p = \dfrac{{a + e + bw}}{{2b}}$可得

同时，可以求得制造商和零售商的利润为

四、 零售商公平偏好下的低碳供应链减排与定价

如果零售商具有公平偏好，此时存在两种情况：一是零售商的公平偏好问题引起制造商的重视，并在决策中予以考虑；二种是这种公平偏好并未引起制造商的重视，制造商在其决策中未予以考虑。

（一） 制造商考虑零售商公平偏好时低碳供应链减排与定价

如果制造商考虑零售商的公平偏好，此时在供应链决策中零售商在关注自身所获得利润的同时也关注利润分配是否公平。此时，效用最大化是零售商的目标函数，即

将${\pi _{\rm{M}}} \,=\, \left( {w \,-\, c} \right)\left( {a \,-\, bp + e} \right) - \left( {\sigma - e} \right)t - \dfrac{1}{2}k{e^2}$和${\pi _{\rm{R}}} = \left( {p - w} \right)\left( {a - bp + e} \right)$代入式（9），并进行整理可得

式（10）对p求二阶导数，可得$\dfrac{{{\partial ^2}{\mu _{\rm{R}}}}}{{\partial p}} < 0$，所以式（10）所表示的目标函数存在最优解，令$\dfrac{{\partial {\mu _{\rm{R}}}}}{{\partial p}} = 0$，可得

接着，制造商根据零售价格来确定产品的批发价格和减排量，此时制造商的目标函数为

将式（11）代入式（12），进行整理可得

由于海赛矩阵${\boldsymbol{H}} = \left[ {\begin{array}{*{20}{c}} {\dfrac{{{\partial ^2}{\pi _{\rm{M}}}}}{{\partial {w^2}}}}&{\dfrac{{{\partial ^2}{\pi _{\rm{M}}}}}{{\partial w\partial e}}} \\ {\dfrac{{{\partial ^2}{\pi _{\rm{M}}}}}{{\partial e\partial w}}}&{\dfrac{{{\partial ^2}{\pi _{\rm{M}}}}}{{\partial {e^2}}}} \end{array}} \right] =$ $\left[ {\begin{array}{*{20}{c}} { - \dfrac{b}{{2(1 + \lambda )}}}&{ - \dfrac{1}{2}} \\ { - \dfrac{1}{2}}&{ - k} \end{array}} \right]$，其一阶顺序主子式为$- \dfrac{b}{{2(1 + \lambda )}} < 0$，二阶顺序主子式为$\dfrac{{bk}}{{2(1 + \lambda )}} - \dfrac{1}{4}$，所以当$\dfrac{{bk}}{{1 + \lambda }} > \dfrac{1}{2}$时，海赛矩阵为负定的，因此式（13）所表示的制造商目标函数存在最优解。用上标$- $*表示制造商考虑零售商公平偏好时的最优决策。

令$\dfrac{{\partial {\pi _{\rm{M}}}}}{{\partial e}} = 0,\dfrac{{\partial {\pi _{\rm{M}}}}}{{\partial w}} = 0$ ，可得

将式（14）代入式（11），可以求得产品的零售价格为

同时，可以求得制造商和零售商的利润为

将$ {\overline w ^*} $，$ {\overline p ^*} $和$ {\overline e ^*} $分别对$ \lambda $求导，在目标函数存在最优解的条件下，即满足$\dfrac{{bk}}{{1 + \lambda }} > \dfrac{1}{2}$时，可以求得$\dfrac{{\partial {{\overline w }^*}}}{{\partial \lambda }} =$ $- \dfrac{{8bk(ak - bck + t)}}{{{{\left[ {1 + \lambda - 4b(k + 2k\lambda )} \right]}^2}}} < 0,\dfrac{{\partial {{\overline p }^*}}}{{\partial \lambda }} = - \dfrac{{3(ak - bck + t)}}{{{{\left[ {1 + \lambda - 4b(k + 2k\lambda )} \right]}^2}}} < 0$， $\dfrac{{\partial {{\overline e }^*}}}{{\partial \lambda }} = - \dfrac{{4b(ak - bck + t)}}{{{{\left[ {1 + \lambda - 4b(k + 2k\lambda )} \right]}^2}}} < 0$。

据此，可得结论2：如果制造商考虑零售商的公平偏好，此时零售商公平偏好越强，产品减排量、批发和零售价格越低；随着零售商公平偏好强度的减少，产品减排量、批发和零售价格不断上升。

结论2表明：如果制造商在供应链的决策过程中考虑零售商的公平偏好，那么公平偏好可以作为零售商提升其在供应链中地位的工具，提高与制造商在议价方面的优势，进而提高利润。随着零售商公平偏好强度的增加，制造商所确定的产品减排量不断下降。形成这一现象的主要原因在于，如果零售商具有公平偏好，在决策中更加关注利润分配的公平性，那么制造商在决策中就需要考虑零售商的这种公平偏好，所以零售商与制造商谈判的砝码增强，这就提升了零售商的议价能力，议价能力随着其公平偏好的增加而上升，产品批发价格必然降低，而此时降低碳排放量所带来的销量增加给制造商增加利润不足以弥补其减排成本，因此为了获取较高的利润，制造商就不断降低其产品的减排量。由此说明，零售商的公平偏好在一定程度上阻碍了产品减排，因此需要政府宣传低碳产品的优势，使零售商将关注焦点从利润分配的公平性转移到产品的低碳情况上，降低其公平偏好，促进产品减排。

将$\overline{\pi}_{{\rm{M}}}^{*}$和${\overline{\pi}}_{{{\rm{R}}}}^{*}$分别对$ {\lambda} $求偏导数，在目标函数存在最优解的条件下，即满足$\dfrac{{bk}}{{1 + \lambda }} > \dfrac{1}{2}$时，可得$\dfrac{f{\overline{\pi}}_{{{\rm{M}}}}^{*}}{f {\lambda}} < 0, \dfrac{f{\overline{\pi}}_{{{\rm{R}}}}^{*}}{f{\lambda}} > 0$。

据此，可得结论3：在制造商考虑零售商公平偏好的情况下，制造商利润与零售商公平偏好负相关，零售商利润与其公平偏好正相关。

结论3表明：公平偏好会影响制造商和零售商的利润分配情况，他们之间存在一个此消彼长的情况。然而，在实际的供应链运作中，制造商和零售商在市场竞争中的地位直接决定了零售商的公平偏好强度。

（二） 制造商不考虑零售商公平偏好时低碳供应链减排与定价

在制造商不考虑零售商的公平偏好的情况下，制造商认为零售商的决策目标是其利润最大化，制造商以此作为前提条件来确定自身的最优决策，用上标^*表示制造商不考虑零售商公平偏好时的最优决策，即${\hat w^*} = {w^*} = \dfrac{{2ak + 2bck + 2t - c}}{{4bk - 1}}$，${\hat e^*} = {e^*} = \dfrac{{4bt + a - bc}}{{4bk - 1}} $，而实际上零售商是具有公平偏好的，在这种情况下，零售商的决策目标是其所获得的效用最大化，即零售商使用公式（9）来确定其最优策略，可得

将$ \hat{w}^{*} $，$ \hat{e}^{*} $和$ \hat{p}^{*} $代入利润函数，可得

分别将$ \hat{p}^{*}$，$ \hat{w}^{*} $和$ \hat{e}^{*} $对${\lambda} $求偏导数可得$\dfrac{f \hat{p}^{*}}{f \lambda} > 0$，$ \dfrac{f \hat{w}^{*}}{f \lambda}=0 $，$ \dfrac{f \hat{e}^{*}}{f \lambda}=0 $。

据此，可得结论4：产品的零售价格在制造商不考虑零售商公平偏好的情况下与零售商的公平偏好正相关，而制造商所确定的产品的批发价格和产品的减排量与零售商公平偏好无关。

结论4表明：如果制造商不考虑零售商公平偏好，零售商公平偏好不会对其决策产生影响。随着公平偏好强度的增加，零售商会逐步提高零售价格，期望获得更多利润，但是产品零售价格的上升必然导致产品销量的下降，对提升产品的市场占有率不利。

将$ \hat{\pi}_{{\rm{M}}}^{*} $和$\hat{\pi}_{{\rm{R}}}^{*} $分别对$ {\lambda} $ 求偏导数可得$\dfrac{f \hat{\pi}_{{\rm{M}}}^{*}}{f \lambda} < 0$，$ \dfrac{f \hat{\pi}_{{\rm{R}}}^{*}}{f \lambda}< 0 $。

据此，可得结论5：如果制造商在进行减排与定价决策时不考虑零售商公平偏好的影响，制造商和零售商的利润与零售商的公平偏好负相关。

结论5表明：双方在供应链博弈过程中的信息不对称是形成这一现象的主要原因，制造商在进行决策时以零售商无公平偏好作为前提，而零售商实际上是具有公平偏好的，这就易造成制造商与零售商在博弈过程中的信息不对称。这种信息不对称对双方决策的影响都是负面的，会同时降低双方利润，同时公平偏好越大，双方利润下降幅度就越大。

（三） 比较分析

分析上述三种情况下的低碳供应链的定价与减排决策，可以得出以下两条结论。

结论6：三种情况下产品的批发价格和零售价格满足$ w^{*}=\hat{w}^{*}>\overline{w}^{*} $，$ \hat{p}^{*}>p^{*}>\overline{p}^{*} $，$ {e}^{*}=\hat{{e}}^{*} > \hat{e}^{*} $

结论6表明：一是产品价格在无公平偏好情况与制造商不考虑零售商公平偏好情况相等，但是如果制造商在进行减排与定价决策时考虑零售商公平偏好的影响，此时制造商所确定的产品批发价格会受零售商公平偏好的影响，此时产品的批发价格会逐步降低。二是如果制造商不考虑零售商公平偏好，那么此时零售价格最高；如果制造商考虑零售商的公平偏好，那么此时零售价格最低。三是在零售商无公平偏好时产品减排量等于制造商不考虑零售商公平偏好时的减排量。如果制造商考虑零售商的公平偏好，此时零售商会利用其公平偏好与制造商讨价还价，要求降低产品的批发价格，因此制造商为了降低成本，会逐步降低产品的减排量。

结论7：三种情况下制造商和零售商的利润满足$ \pi_{{\rm{M}}}^{*}> \overline{\pi}_{{\rm{M}}}^{*}>\hat{\pi}_{{\rm{M}}}^{*} $，$ \overline{\pi}_{{\rm{R}}}^{*}>\pi_{{\rm{R}}}^{*}>\hat{\pi}_{{\rm{R}}}^{*} $。

结论7表明：一是站在制造商视角，制造商利润在无公平偏好时最高。如果零售商具有公平偏好，那么制造商在决策时应考虑其影响，这样能提高制造商利润。二是站在零售商视角，零售商利润在制造商考虑其公平偏好时最好。这就说明，零售商应尽量让制造商知晓其公平偏好，使公平偏好引起制造商关注，并在决策中予以考虑，这样对零售商最为有利。

五、 数值分析

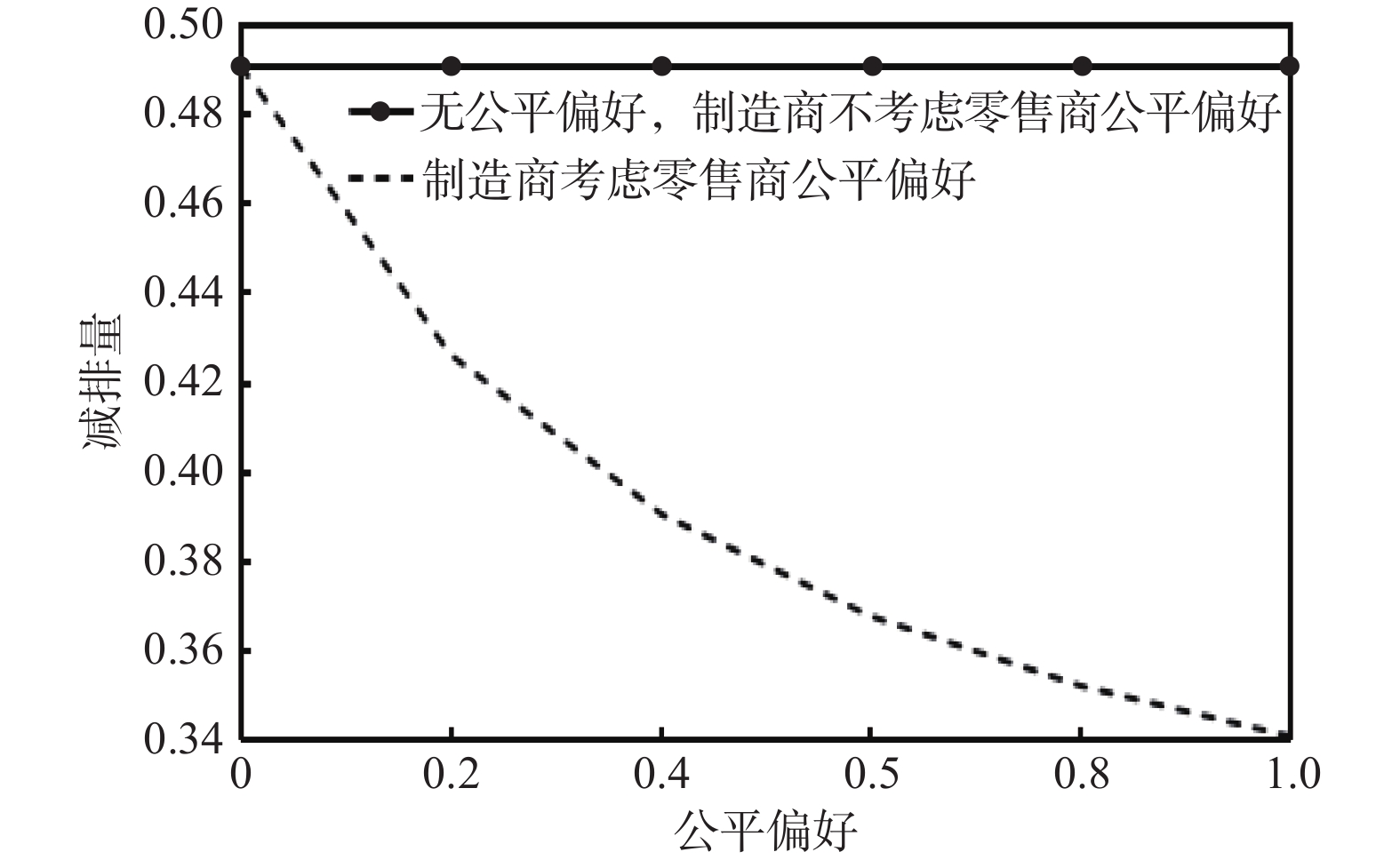
笔者使用数值分析的方法来分析公平偏好是如何影响相关决策变量的。令$ a = 300 $，$ b = 3 $，$ c = 10 $，$ k = 50 $，$ t = 2 $，$ \sigma = 5 $，可以得到三种情况下零售商公平偏好对减排量、制造商的利润和零售商的利润的影响。

零售商公平偏好对减排量的影响，如图2所示。由图2可知，如果制造商考虑零售商公平偏好，此时产品减排量与公平偏好负相关，并且在这种情况下的产品减排量低于其他两种情况，这表明零售商公平偏好对降低碳排放不利，因此，需要政府宣传低碳产品的优势，使零售商将关注焦点从利润分配的公平性上转移到产品的低碳情况上，降低其公平偏好，促进产品减排。

图  2  零售商公平偏好对减排量的影响

下载: 全尺寸图片 幻灯片

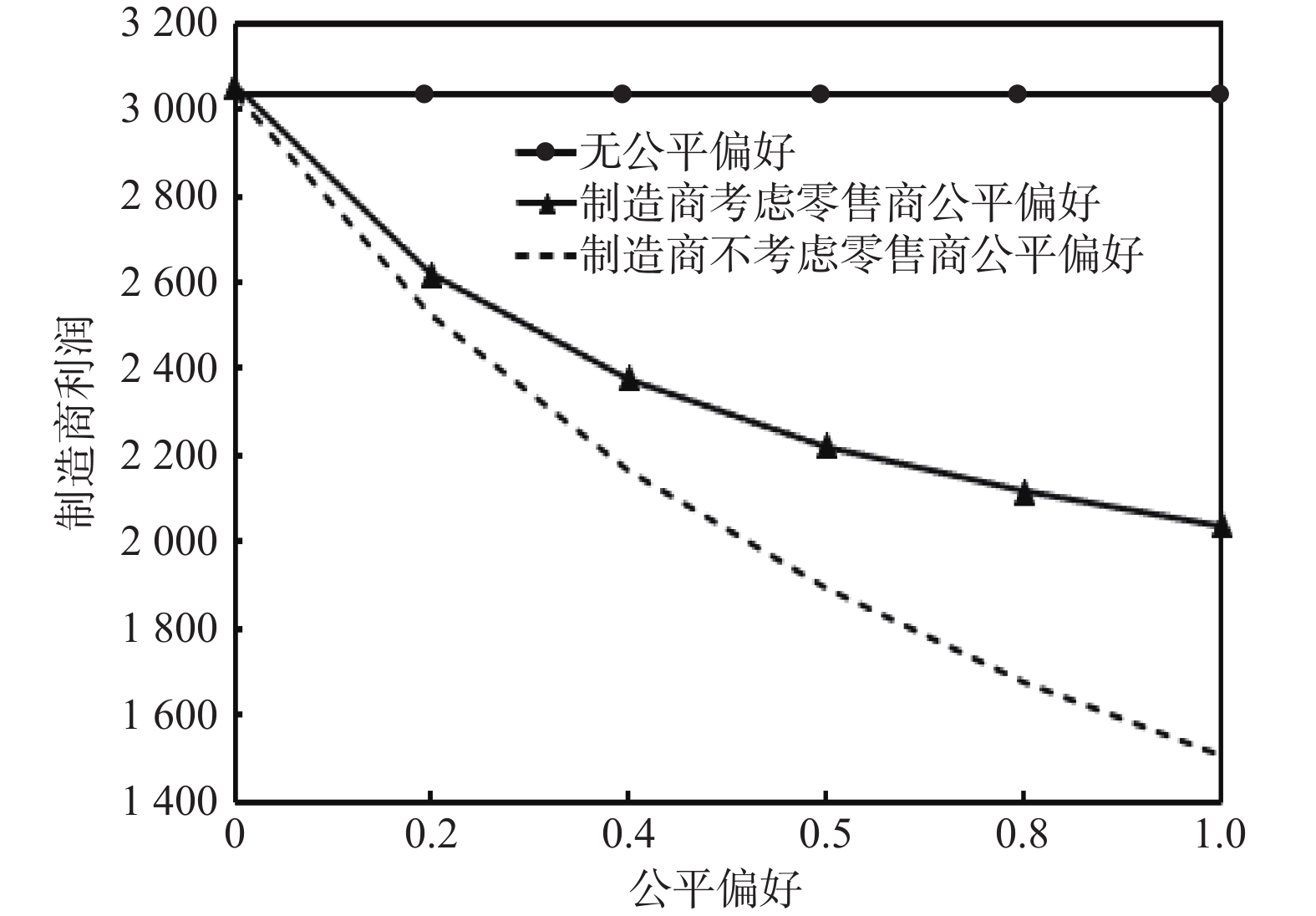
零售商公平偏好对制造商利润的影响，如图3所示。由图3可知，制造商利润与零售商公平偏好负相关，零售商公平偏好越高，制造商利润就越低。同时还可以发现，如果零售商具有公平偏好，制造商利润在考虑零售商公平偏好的情况下较大，这就表明，在零售商具有公平偏好的情况下，制造商在决策中应该予以考虑，只有这样才能帮助制造商增加利润。

图  3  零售商公平偏好对制造商利润的影响

下载: 全尺寸图片 幻灯片

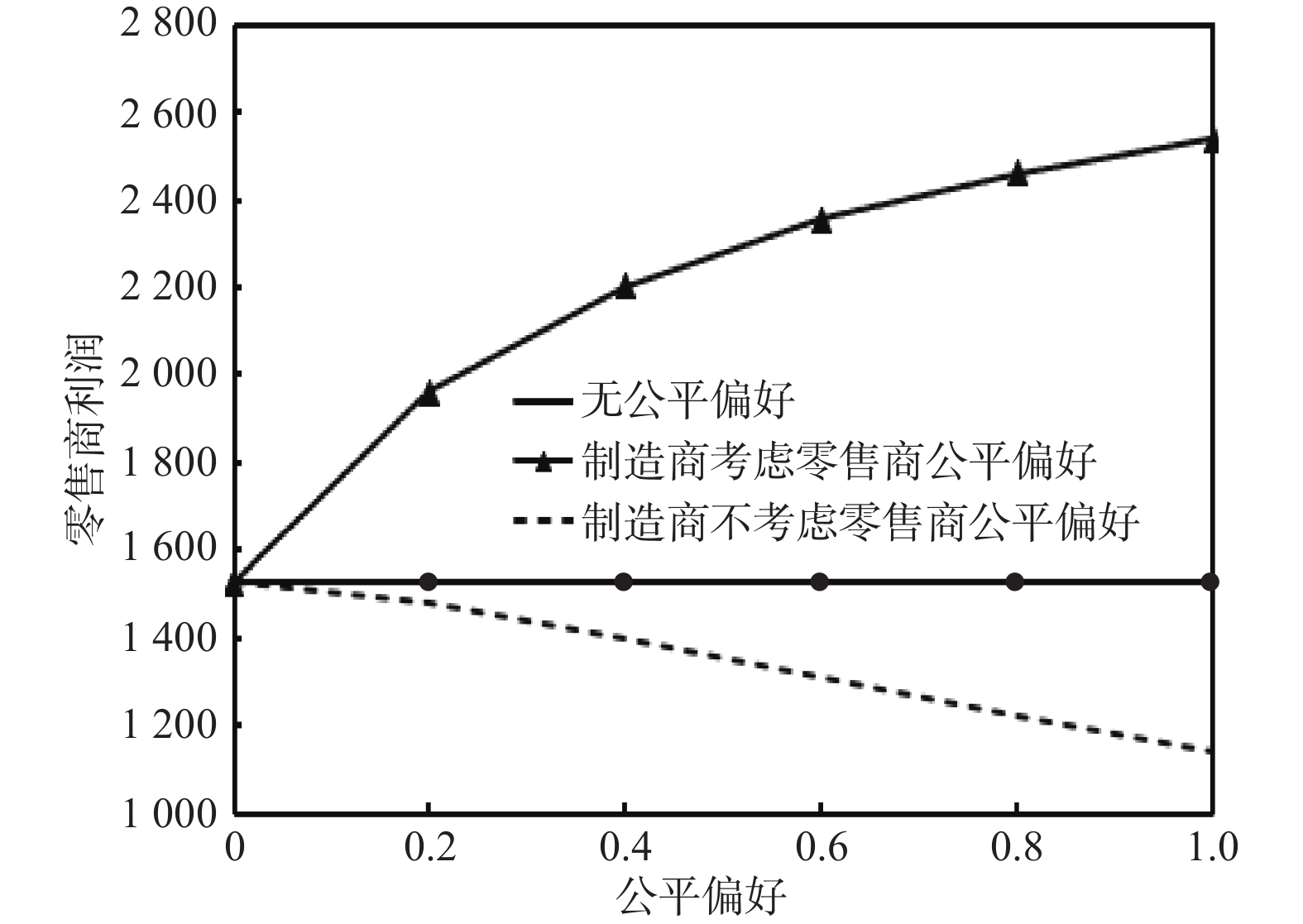
零售商公平偏好对零售商利润的影响，如图4所示。由图4可知，如果制造商考虑零售商公平偏好，那么零售商利润与公平偏好正相关。如果制造商不考虑零售商公平偏好，那么零售商利润与其公平偏好负相关。同时还可以发现，在零售商无公平偏好情况下，零售商利润介于其他两种情况之间，这就表明，零售商公平偏好是否能够提高利润主要受制造商的影响，在制造商考虑零售商公平偏好的情况下，公平偏好对零售商有利，反之则不利。综合图3和图4可以发现，在零售商具有公平偏好的情况下，制造商应该在决策中予以考虑，只有这样才能同时提高双方的利润，实现双赢。

图  4  零售商公平偏好对零售商利润的影响

下载: 全尺寸图片 幻灯片

六、 结论

笔者将零售商公平偏好引入供应链的减排与定价决策中，研究了零售商无公平偏好、制造商考虑零售商公平偏好和制造商不考虑零售商公平偏好三种情况下供应链减排与定价决策。研究发现：首先，零售商公平偏好越大，产品减排量越小，这就说明，公平偏好在一定程度上阻碍了产品减排，因此需要政府宣传低碳产品的优势，使零售商把关注焦点从利润分配的公平性转移到产品的低碳情况上，降低其公平偏好，促进产品减排；其次，在制造商考虑零售商公平偏好的情况下，公平偏好可以作为零售商提高其地位的工具，提高与制造商在议价方面的优势，增加其利润水平；最后，如果零售商具有公平偏好，那么制造商应该予以考虑，这样既可以提高制造商的利润，又可以提高零售商利润，实现双赢。

笔者只考虑了零售商的公平偏好，但是上游制造商同样会具有公平偏好，未来在研究单向公平偏好的基础上，将继续探讨双向考虑公平博弈问题。同时，在双向偏好博弈条件下，将进一步分析零售商的市场地位对决策的影响，即零售商处于优势地位、制造商和零售商地位平等、零售商处于劣势地位三种情况下的博弈模型变化。