Incentive and Constraint Pricing Design of Equipment Research Taking Cost Risk into Account
-
摘要:
带有激励约束机制的装备科研合同定价模式能够较好地适应因科研项目不确定性所带来的成本风险,而激励系数的确定是其中的关键设计。在总结和比较典型的激励约束定价设计的基础上,针对激励系数设计与科研成本风险分析未能有效结合的问题,基于项目工作分解结构(WBS),采用模拟仿真方法得到项目成本概率分布,考虑成本风险大小给出装备科研价格激励约束原则,结合成本概率分布的分位数选择成本上下限,进而确定激励系数和约束系数。同时,还进行了实例分析,结果验证了研究方法的有效性。
-
关键词:
- 装备科研 /
- 成本风险 /
- 激励约束定价 /
- 工作分解结构(WBS) /
- 激励系数
Abstract:The equipment research contract pricing model with incentive and constraint mechanism can better adapt to the price risk caused by the uncertainty of research projects, and the determination of incentive coefficient is the key of the model design. To solve the problem that incentive coefficient design is not combined effectively with the research cost risk analysis, the paper obtains the project cost probability distribution with the help of simulation method and the project work breakdown structure (WBS) after summarizing and comparing the typical incentive and constraint pricing designs. The paper also takes cost risk into account, and establishes the incentive and constraint principles of equipment research price. Based on the quantiles of the cost probability distribution, the upper and lower limits of the project cost are selected to determine the incentive and constraint coefficients. In addition, the paper carries out a case analysis to illustrate the effectiveness of the research method.
-
一、 文献综述
中国军队目前的装备科研定价机制较为单一,通常是在研制早期测算价格后,采用固定价格合同方式与承制单位签订合同。这一定价机制看似是将成本风险转移给了承制单位,但由于研制过程中存在大量的内外部不确定性因素,并且装备研制很多时候是双边垄断情形,往往造成一旦研制经费开支远超合同价格,承制单位会以各种理由要求追加经费,使得本应由承制单位承担的成本风险转嫁给了军方,造成科研经费使用效益不高,定价机制与成本风险脱节的现象。不同的成本风险应匹配不同的合同定价模式:固定价格合同下风险全部由承制单位承担,适用于不确定性较小的项目;成本补偿合同下风险完全由军方承担,适用于不确定性较大的项目。而对于风险较大的科研项目,可在固定价格合同、成本补偿合同中引入激励定价机制,即固定价格加激励金合同或成本补偿加激励金合同。激励系数的确定是其中的关键设计,关系军方和承制单位对科研项目经济收益或损失的分配比例[1]。
哈特利和桑德勒较为系统地论述了国防采购中的激励理论原理,给出了基于委托—代理理论的单代理人和多代理人激励模型,为激励理论在国防采购领域的应用提供了借鉴[2]。一直以来,美军强调与军品承制单位“共担成本、共享利益”的激励定价思想,事先与承制单位确定利润分配比例或酬金额度,然后在军品生产完成后根据承制单位实际消耗成本等,确定有利于供需双方的军品价格[3]。Berends运用效用理论,对于成本加补偿激励酬金合同,建立绩效与利润率正相关的量化模型,并求解模型确定成本激励系数[4];Broome和Perry对成本激励系数的确定进行实证研究,同时提出了成本激励系数在不同因素影响下取值不同的观点[5];Nguyen等采用系统工程方法,基于对国防部采购项目激励定价进行探讨,构建数学模型求解得到最优激励参数[6]。
国内学者借鉴美军的多种激励约束定价机制,对中国军队武器装备激励约束定价机制进行了研究。董齐光等总结了美军三项激励约束定价机制的原理,为中国军队激励性定价方法的设计提供了思路[7]59-62;吴诗辉等在对美军与中国军队激励约束定价模式进行对比分析的基础上,提出在承制单位期望利润、军方期望价格的基础上协商确定激励系数[8]134-148;林名驰等采用委托—代理理论建立了按完工效果直接给予报酬合同、按固定份额分成合同、按约定公式分成合同三类目标价格合同模式的激励模型,并采用规划方法给出了模型最优解[9];訾书宇等建立了基于成本估算风险的装备激励价格合同模式,促使承制单位对其过于乐观的成本估算或者不佳的成本表现负责,使其在装备研发前提供更为客观的成本建议,降低成本超支风险[10];孙胜祥和韩霜从成本、质量、工期三个维度开展激励,明确“目标价格+多因素激励约束利润”的价格构成形式,提出了多因素激励约束议价方法[11]1338-1347。
总体来看,国内外学者在装备激励约束定价领域的研究大多集中于装备生产订购方面,且往往脱离成本风险单纯谈激励约束定价方法,激励约束系数主要由人为主观确定或通过建立线性激励约束模型求解,激励约束系数设计未能结合项目的成本风险,也未能反映承制单位成本控制的努力程度。鉴于此,笔者拟基于科研项目分解结构和成本风险评估,尝试从成本风险和成本控制的角度给出激励约束系数的确定原则和方法。
二、 激励约束定价设计原理
激励约束定价方法将军方与承制单位的利益和风险统筹考虑,通过分摊成本节约值的方式,鼓励承制单位积极进行过程成本控制和管理创新。当承制单位过程管控得力从而实现成本节约时,承制单位可以分享成本的节约值从而获得更多的利润,军方也可以从成本的节约值中分享收益,实现双方共赢;当承制单位因管理不善、过程成本监控不当导致成本超支时,承制单位分担超支部分的一定损失,以减少军方的亏损风险。通过事前确定定价方法和相关指标,可以全过程督促承制单位进行成本控制。
(一) 典型的激励约束设计
激励约束定价的价格方案为定价成本、目标利润(目标成本的一定比例)、激励约束利润三者之和,计算公式为
$$ P = C + a({C_{\rm{T}}} - C) + b{C_{\rm{T}}} $$ (1) 式中:
$P$ 为装备价格;${C_{\rm{T}}}$ 为目标成本;$C$ 为定价成本;$a({C_{\rm{T}}} - C)$ 为激励约束利润,$a$ 为合同双方协商确定的激励约束系数,即成本分摊系数,$a \in [0,1]$ ;$b{C_{\rm{T}}}$ 为目标利润,$b \in [0,1]$ ,通常$b$ 的取值为0.05。为了避免极端情况的出现,根据具体项目情况,设置价格上下限或成本上下限,或设置利润上下限。
1. 设置价格上限或成本上限的情况
为了避免军方承受过大的损失,降低风险,可以设置价格上限
${P_{\rm{U}}}$ ,此时成本上限$C_{\rm{U}}$ 为$$ {C_{\rm{U}}} = \frac{{{P_{\rm{U}}} - (a + b){C_{\rm{T}}}}}{{1 - a}} $$ (2) 定价成本超过成本上限部分全部由承制单位承担,公式为
$$\left\{\begin{array}{l} P = {P_{\rm{U}}}\\ C \gt {C_{\rm{U}}} \end{array}\right.$$ (3) 2. 设置价格下限或成本下限的情况
为了鼓励承制单位控制成本,可以设置价格下限
${P_{\rm{D}}}$ ,此时成本下限$C_{\rm{D}} $ 为$$ {C_{\rm{D}}} = \frac{{{P_{\rm{D}}} - (a + b){C_{\rm{T}}}}}{{1 - a}} $$ (4) 定价成本小于成本下限部分全部由承制单位享有,公式为
$$\left\{\begin{array}{l} P = {P_{\rm{D}}}\\ C \lt {C_D} \end{array}\right.$$ (5) 3. 设置利润上限的情况
为了控制承制单位获得超额利润,可以协商制定利润上限
$E_{\rm{U}} $ ,${E_{\rm{U}}} = A{C_{\rm{T}}}$ ,其中,A为利润上限与目标成本的比率,$0 \lt A \lt a + b $ 。此时成本下限为$$ {C_{\rm{D}}} = \frac{{(a + b - A){C_{\rm{T}}}}}{a} $$ (6) 定价成本小于成本下限,利润至多为
$A{C_{\rm{T}}}$ ,公式为$$ \left\{\begin{array}{l} P = C + A{C_{\rm{T}}}\\ C \lt {C_D} \end{array}\right.$$ (7) 4. 设置利润下限的情况
为了避免承制单位承受过大损失,可以协商制定利润下限
$E_{\rm{D}} $ ,${E_{\rm{D}}} = B{C_{\rm{T}}}$ ,其中,B为利润下限与目标成本的比率,$B \lt a + b $ 。此时成本上限为$$ {C_{\rm{U}}} = \frac{{(a + b - B){C_{\rm{T}}}}}{a} $$ (8) 定价成本超过成本上限后,利润保持为
$B{C_{\rm{T}}}$ ,公式为$$\left\{\begin{array}{l} P = C + B{C_{\rm{T}}}\\ C \gt {C_{\rm{U}}} \end{array}\right.$$ (9) 在上述各种情况下,当定价成本
$C \in [{C_{\rm{D}}},{C_{\rm{U}}}]$ 时,$P = C + a({C_{\rm{T}}} - C) + b{C_{\rm{T}}}$ 。这种典型激励约束方法的固定激励约束系数设置较为主观,一般设为0.5,承制单位节约和超支激励强度相同,对于超支风险较大的装备项目,承制单位可能存在畏难情绪,从而增加了目标价格协商的难度,同时,装备成本随着承制单位努力程度增加而降低的速度越来越慢,固定的激励系数无法实现激励力度与承制单位努力水平之间的匹配。
(二) 结构性利润分析方法
为了更好地发挥激励约束定价对装备承制单位的激励作用,促进承制单位积极开展技术创新并提高管理水平,对承制单位成本节约和成本超支的不同情况,采取不同的激励系数的方法,即结构性利润分析方法[7]59-62[8]134-148。军方根据武器装备建设的经费投入,使用类推法、参数法、工程法等方法,对武器装备目标成本
${C_{\rm{T}}}$ 、成本上限${C_{\rm{U}}}$ 、成本下限${C_{\rm{D}}}$ 等进行测算,作为过程成本控制和价格确定的依据。同时,对目标利润${E_{\rm{T}}}$ 、利润上限${E_{\rm{U}}}$ 、利润下限${E_{\rm{D}}}$ 等进行合理确定。激励约束系数的确定过程如下:1. 定价成本低于目标成本
当定价成本
$C$ 低于目标成本${C_{\rm{T}}}$ 时,考虑目标成本与定价成本的差额和利润成固定的线性关系,且定价成本达到成本下限时,此时的利润应等于利润上限,即激励系数${a_1}$ 满足${a_1}({C_{\rm{T}}} - {C_{\rm{D}}}) + {E_{\rm{T}}} = {E_{\rm{U}}}$ ,可推得$$ {a_1} = \frac{{{E_{\rm{U}}} - {E_{\rm{T}}}}}{{{C_{\rm{T}}} - {C_{\rm{D}}}}} \times 100\% $$ (10) 2. 定价成本高于目标成本
当定价成本
$C$ 高于目标成本${C_{\rm{T}}}$ 时,同样考虑定价成本与目标成本的差额和利润成固定的线性关系,在定价成本达到成本上限时,此时的利润应等于利润下限,即激励约束系数${a_2}$ 满足${a_2}({C_{\rm{T}}} - {C_{\rm{U}}}) + {E_{\rm{T}}} = {E_{\rm{D}}}$ ,可推得$$ {a_2} = \frac{{{E_{\rm{D}}} - {E_{\rm{T}}}}}{{{C_{\rm{T}}} - {C_{\rm{U}}}}} \times 100\% $$ (11) 在结构性利润分析方法中,目标成本和成本上下限的确定是通过参数法、类推法、工程法等论证得来的,对成本的不确定性虽做了一定的论证,但未能对成本风险加以深入的定量考察。因而,对于成本上下限的确定以及对激励约束系数的设计,是无法根据项目成本风险进行动态调整的。
三、 基于成本风险的激励约束系数设计
在典型的激励约束设计中,激励约束系数固定的设计是根据价格上下限或利润上下限以及激励约束系数来推导成本上下限的,而结构性利润分析方法是根据成本上下限和利润上下限来分别确定成本节约的激励系数和成本超支的约束系数的。由于目标成本和成本上下限是合理估算经费需求的一个基础,以此来制定灵活的激励约束系数更为合理;反之,由固定的激励约束系数来反推成本上下限不符合认识的规律,主观性太强,且激励和约束的强度一致并不符合通常的奖惩机制。
同时,军方更为合理的考虑是,对于成本风险大的科研项目,为了鼓励承研单位控制成本,当承研单位的成本控制得较好时,相较于成本控制得不好时的约束,应给予更大的激励;而对于成本风险小的科研项目,为了防止承研单位不努力控制成本,当承研单位的成本控制得不好时,相较于成本控制得好时的激励,应给予更大的约束。由于科研项目成本的不确定性可以用成本概率分布描述,通过考虑项目成本概率分布函数,应用风险评价方法研究确定目标成本、成本上下限,进而确定激励约束系数。
(一) 基于WBS的科研项目成本风险估计
根据最新的装备研制经费管理规定,项目要以评审通过的项目立项综合论证报告、研制策划报告等技术文件为基本依据,开展项目工作分解,按照规定的成本内容进行各子项目经费概算,最终汇总形成项目经费概算方案,即需要从成本构成和科研内容两个维度开展科研概算价格论证,明晰各项科研内容和概算价格的对应关系,说明科研项目技术与经济之间紧密的联系和影响。只有做好项目工作分解,才能做好后续的成本风险评估、合同选择和激励条款设计工作。
工作分解结构(WBS)是对武器装备项目在研制过程中应完成的工作进行自上而下逐级分解所形成的一个层次体系。该层次体系以研制的产品为中心,由产品(硬件和软件)项目、服务项目和资料项目组成,且完全限定了武器装备项目的工作,并表明了各项工作之间以及它们与最终产品之间的关系。在武器装备研制过程中,应随工程的进展制订相应的WBS:在论证阶段,使用部门应根据该阶段系统工程工作的结果,提出初步的工程项目纲要WBS(通常为WBS最上面3个层次);在方案阶段,在总体方案形成过程中,研制单位会同使用部门一起对初步的工程项目纲要WBS进行修改,到此阶段结束时,修改后的工程项目纲要WBS随研制任务书草案和研制方案论证报告在上报审批后,形成批准的工程项目纲要WBS。
在项目工作分解的基础上,可以通过了解较低等级WBS单元的成本情况,进而了解项目的整体成本情况,为了既能发挥项目工作分解精细化的优势,又能较好地定量化掌握项目的成本概率分布,可以应用系统仿真方法进行建模分析,利用较低等级WBS单元各个单元成本的概率分布函数,通过蒙特卡洛仿真调用相应概率分布的随机数发生器产生各单元的成本随机数,并进行叠加[11]1338-1347。独立、重复进行多次仿真,对仿真输出结果进行统计分析,获得项目级总成本的各种估计值和累计成本概率分布函数,由此确定成本超支的实际风险水平。具体步骤如下:
1. 工作结构分解
利用WBS方法将系统或项目分解到较低等级工作单元。选择在哪一级,作为最低级别取决于项目所处的阶段,在研制初期,一般不会超过2级或3级,即形成工程项目纲要WBS。
2. 确定各单元成本概率分布函数
确定每一个WBS单元的成本概率分布函数。由于项目研制初期,成本还未实际发生,因此,需要综合应用工程法、参数法、类比法等评估每一个WBS单元的成本,通过技术专家、财务专家、成本分析员与各WBS单元的管理人员共同合作,研究各单元的研制费用的最低值、最可能值、最高值,并采用三角分布形式进行处理[12-13],由此得到各单元的成本概率分布函数。
3. 蒙特卡洛仿真
运用蒙特卡洛仿真方法,根据各WBS单元的成本概率分布函数,调用相应概率分布的随机数发生器产生各单元的成本随机数,并进行项目级总成本的叠加,即
$C = \sum {{C_i}} $ ,其中,${C_i}$ 为WBS单元的成本。为了得到总成本的概率分布,必须进行多次独立、重复的仿真运行。4. 项目级总成本的统计分析
对仿真输出获得的项目级总成本进行点估计(均值和方差)、区间估计(置信区间)、总成本的概率分布拟合检验、总成本的累计概率分布和风险概率分布的统计分析。
假设运用WBS方法与蒙特卡洛仿真方法,得到项目定价成本
$C$ 服从均值为$\hat \mu $ 和标准差为$\hat \sigma $ 的正态分布,即$C\sim N(\hat \mu ,\hat \sigma )$ ,则项目在预算成本${C_{\rm{b}}}$ 下完成研制任务的概率为$$ P(C \leqslant {C_{\rm{b}}}) = P\left( {\frac{{C - \hat \mu }}{{\hat \sigma }} \leqslant \frac{{{C_{\rm{b}}} - \hat \mu }}{{\hat \sigma }}} \right) = \varPhi \left(\frac{{{C_{\rm{b}}} - \hat \mu }}{{\hat \sigma }}\right) $$ (12) 成本风险度为变异系数
${{C}}_{\rm{v}} = \dfrac{{\hat \sigma }}{{\hat \mu }}$ 。变异系数越小,成本概率分布越集中于
$\hat \mu $ 附近,成本风险越小;变异系数越大,成本概率分布越平坦,成本风险越大。通常,可以认为变异系数${{C}}_{\rm{v}} $ <5%,成本风险小;5%$\leqslant{{C}}_{\rm{v}} $ <10%,成本风险一般;10%<${{C}}_{\rm{v}} \leqslant$ 25%,成本风险较大;${{C}}_{\rm{v}} $ >25%,成本风险高。(二) 激励约束系数设计
为了便于分析,假设利润上下限相较于目标利润是对称的,即
${E_{\rm{T}}} - {E_{\rm{D}}} = {E_{\rm{U}}} - {E_{\rm{T}}}$ 。根据项目成本的风险设计成本上下限,由于成本控制水平是随着成本承制单位努力程度增加而逐渐降低的,所以成本上下限的设计应是非对称的。目标成本是项目成本的预期目标,可以将目标成本设置为项目成本随机变量的期望值,即${C_{\rm{T}}}{\text{ = }}\hat \mu $ 。假设定价成本在成本下限与目标成本之间时,目标成本与定价成本之间的差额和利润成固定的线性关系,且定价成本达到成本下限时,利润应等于利润上限,即激励系数
${a_1}$ (0<${a_1}$ <1)满足${a_1}(\hat \mu - {C_D}) + {E_{\rm{T}}} = {E_{\rm{U}}}$ ;定价成本在成本上限和目标成本之间时,定价成本与目标成本之间的差额和利润成固定的线性关系,在定价成本达到成本上限时,利润应等于利润下限,即约束系数${a_2}$ (0<${a_2}$ <1)满足${a_2}(\hat \mu - {C_{\rm{U}}}) + {E_{\rm{T}}} = {E_{\rm{D}}}$ 。需要强调的是,对于利润上下限的设计,除考虑军方和承研单位的利益诉求外,还应满足利润上限与目标利润的差额小于目标成本与成本下限的差额,以及利润下限与目标利润的差额小于成本上限与目标成本的差额的关系,从而保证激励系数和约束系数均小于1。由此推得:
1. 定价成本低于目标成本
当定价成本
$C$ 低于目标成本$\hat \mu $ 时,激励系数的计算公式为$$ {a_1} = \frac{{{E_{\rm{U}}} - {E_{\rm{T}}}}}{{\hat \mu - {C_{\rm{D}}}}} \times 100\% $$ (13) 2. 定价成本高于目标成本
当定价成本
$C$ 高于目标成本$\hat \mu $ 时,约束系数的计算公式为$$ {a_2} = \frac{{{E_{\rm{D}}} - {E_{\rm{T}}}}}{{\hat \mu - {C_{\rm{U}}}}} \times 100\% $$ (14) 由项目成本概率分布函数可知,成本下限
${C_{\rm{D}}}$ 所对应的完成研制任务的概率为$$ P(C \leqslant {C_{\rm{D}}}) = P\left( {\frac{{C - \hat \mu }}{{\hat \sigma }} \leqslant \frac{{{C_D} - \hat \mu }}{{\hat \sigma }}} \right) = \varPhi \left(\frac{{{C_{\rm{D}}} - \hat \mu }}{{\hat \sigma }}\right) = \alpha $$ (15) 即
${C_{\rm{D}}}$ 为项目成本概率分布的$\alpha $ 分位数。成本上限
${C_{\rm{U}}}$ 所对应的完成研制任务的概率为$$ P(C \leqslant {C_{\rm{U}}}) = P\left( {\frac{{C - \hat \mu }}{{\hat \sigma }} \leqslant \frac{{{C_U} - \hat \mu }}{{\hat \sigma }}} \right) = \varPhi \left(\frac{{{C_{\rm{U}}} - \hat \mu }}{{\hat \sigma }}\right) = 1 - \beta $$ (16) 即
${C_{\rm{U}}}$ 为项目成本概率分布的$1 - \beta $ 分位数。对于变异系数大的项目,即成本风险大的科研项目,根据相较于成本超支时的约束,成本节约时应给予更大激励的原则,激励系数
${a_1}$ 应大于约束系数${a_2}$ ,根据式(13)和式(14),可推得$\left| {\hat \mu - {C_{\rm{D}}}} \right| \lt \left| {\hat \mu - {C_{\rm{U}}}} \right|$ ,即成本下限${C_{\rm{D}}}$ 偏离均值$\hat \mu $ 的幅度应小于成本上限${C_{\rm{U}}}$ 偏离均值$\hat \mu $ 的幅度,因而可以推导出$\alpha \gt \beta $ ,如选择$ \alpha \text{=3}0\text{%},\beta \text{=2}0\text{%} $ ,即选择的成本下限,使得研制成本不超过该成本下限的概率为30%;选择的成本上限,使得研制成本超过该成本上限的概率为20%,由此确定成本上下限。对于变异系数小的项目,即成本风险小的科研项目,根据相较于成本节约时的激励,成本超支时应给予更大约束的原则,激励系数
${a_1}$ 应小于约束系数${a_2}$ ,根据式(13)和式(14),可推得$\left| {\hat \mu - {C_{\rm{D}}}} \right| \gt \left| {\hat \mu - {C_{\rm{U}}}} \right|$ ,即成本下限${C_{\rm{D}}}$ 偏离均值$\hat \mu $ 的幅度应大于成本上限${C_{\rm{U}}}$ 偏离均值$\hat \mu $ 的幅度,因而可以推导出$\alpha \lt \beta $ ,如选择$ \alpha \text{=2}0\text{%},\beta \text{=3}0\text{%} $ ,即选择的成本下限,使得研制成本不超过该成本下限的概率为20%;选择的成本上限,使得研制成本超过该成本上限的概率为30%。对于变异系数一般的项目,即成本风险一般的科研项目,可以设置激励系数
${a_1}$ 和约束系数${a_2}$ 一致,即成本上下限相对于目标成本是对称的,成本节约的激励强度和成本超支的约束强度一致,如选择$\alpha {\text{ = }}\beta {\text{ = 35\% }}$ ,即选择的成本下限,使得研制成本不超过该成本下限的概率为35%;选择的成本上限,使得研制成本超过该成本上限的概率为35%。综上可知,利润的计算公式为
$$ E = \left\{ \begin{gathered} {E_{\rm{U}}}\begin{array}{*{20}{c}} {}&{}&{\begin{array}{*{20}{c}} {}&{\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{}&{} \end{array}}&{} \end{array}}& {C \lt {C_{\rm{D}}}} \end{array}} \end{array}}&{} \end{array} \\ {a_1}(\hat \mu - C) + {E_{\rm{T}}}\begin{array}{*{20}{c}} {}&{}&{}&{{C_{\rm{D}}} \leqslant C \leqslant \hat \mu } \end{array} \\ {a_2}(\hat \mu - C) + {E_{\rm{T}}}\begin{array}{*{20}{c}} {}&{}&{}&{\hat \mu \leqslant C \leqslant {C_{\rm{U}}}} \end{array} \\ {E_{\rm{D}}}\begin{array}{*{20}{c}} {}&{}&{\begin{array}{*{20}{c}} {}&{\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{}&{} \end{array}}&{} \end{array}} &{C \gt {C_{\rm{U}}}} \end{array}} \end{array}}&{} \end{array} \\ \end{gathered} \right. $$ (17) 装备价格
$P = C + E$ 。四、 实例分析
以某型反水雷系统为例,运用WBS将系统分解为舰载综控系统、探雷系统、灭雷系统、航行体系统、舰载收放系统、专用保障设备这6部分,其中,每个分系统又可分解为3~6个子系统,邀请10名专家参与成本风险论证。
每名专家分别给出每个子系统研制费用的最低值、最可能值、最高值,并计算其平均值,由此得到各子系统成本的三角概率分布函数。运用蒙特卡洛仿真方法,根据各子系统成本的三角概率分布函数,产生各子系统成本的研制费用随机数,累加后得到系统的研制费用。在本例中,共模拟了1000次,得到1000组系统的研制费用数据,经计算,其均值为25438万元,标准差为4562,其激励约束定价设计如下:
将均值25438万元作为目标成本,目标利润取目标成本的5%,为1271.9万元。由于风险度为4562/25438=17.93%,可以判断出项目研制成本风险较大,考虑经费承受范围和激励约束力度,选择
$\alpha $ =35%,$\beta $ =25%,得到成本上下限分别为28515.02万元和23680.17万元,根据实际利润与目标利润的差额应小于定价成本与目标成本差额的关系,以及军方的承受能力,取目标成本的10%作为利润上限,且利润上下限相对于目标利润是对称关系,经计算得到利润上限为2543.8万元,利润下限为0元,进而计算得到激励系数${a_1}$ =72.46%,约束系数${a_2}$ =41.34%。由此装备价格P为$$ P = \left\{ \begin{gathered} C + 2543.8\begin{array}{*{20}{c}} {}&{}&{\begin{array}{*{20}{c}} {}&{\begin{array}{*{20}{c}} {}&{\begin{array}{*{20}{c}} {}&{\begin{array}{*{20}{c}} {}&{\begin{array}{*{20}{c}} {}&{C \lt 23680.17} \end{array}} \end{array}} \end{array}} \end{array}} \end{array}}&{} \end{array} \\ 72.46\% \times (25438 - C) + 1271.9\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}& {23680.17 \leqslant C \leqslant 25438} \end{array}}&{}&{}&{} \end{array} \\ 41.34\% \times (25438 - C) + 1271.9\begin{array}{*{20}{c}} {}& {25438 \leqslant C \leqslant 28515.02}&{}&{} \end{array} \\ C\begin{array}{*{20}{c}} {}&{}&{\begin{array}{*{20}{c}} {}&{\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{\begin{array}{*{20}{c}} {}&{\begin{array}{*{20}{c}} {}&{\begin{array}{*{20}{c}} {}&{\begin{array}{*{20}{c}} {}&{} \end{array}} \end{array}} \end{array}} \end{array}} \end{array}} \end{array}}& {C \gt 28515.02\begin{array}{*{20}{c}} {}&{} \end{array}} \end{array} \\ \end{gathered} \right. $$ (18) 当定价成本大于23680.17万元且小于25438万元时,其成本节约部分的72.46%由承研单位享有;当定价成本小于23680.17万元时,利润为2543.8万元;当定价成本大于25438万元且小于28515.02万元时,其成本超支部分的41.34%由承研单位承担;当定价成本大于28515.02万元时,利润为0元。该激励约束设计可根据成本风险大小灵活设置成本上下限,并很好地体现了对于成本风险大的科研项目,其成本节约所带来的激励大于成本超支所带来的约束的原则。
五、 结语
笔者借助WBS和仿真模拟技术,定量化研究了科研成本风险,在考虑装备科研成本风险和承研单位努力程度的基础上,灵活设计成本上下限,进而确定了激励约束系数,较好地克服了已有研究对科研成本风险定量考察不足、激励约束系数设置主观性强等问题,为更好地实施激励约束定价模式改革提供了思路。
-
[1] 艾克武,韩伯棠,鄢格青,等. 武器装备研制生产合同价格管制[J]. 科研管理,2007(S1): 176—179. [2] 哈特利, 桑德勒. 国防经济学手册: 第1卷[M]. 姜鲁鸣, 沈志华, 卢周来, 等译. 北京: 经济科学出版社, 2001: 315—335. [3] Department of Defense. The defense federal acquisition regulation supplement (DFARS) [EB/OL]. (2022−02−15)[2022−04−22]. .
[4] BERENDS T C. Cost plus incentive fee contracting-experiences and structuring [J]. International Journal of Project Management,2000,18(3): 165—171.
[5] BROOME J,PERRY J. How practitioners set share fractions in target cost contracts [J]. International Journal of Project Management,2002,20(1): 59—66.
[6] NGUYEN T M,TRAN H T,GUILLEN A T,et al. Acquisition war-gaming technique for acquiring future complex systems: Modeling and simulation results for cost plus incentive fee contract [J]. Mathematics,2018,6(3): 1—29.
[7] 董齐光,刘林山,张玉华. 美军武器装备激励约束定价机制研究[J]. 装备学院学报,2012,23(5): 59—62. [8] 吴诗辉,刘晓东,胡博,等. 装备激励约束定价模式机理对比分析与设计[J]. 航空学报,2019,40(7): 134—148. [9] 林名驰,崔学良,訾书宇. 装备采购项目目标价格合同激励效用研究[J]. 海军工程大学学报,2019,31(2): 87—90. [10] 訾书宇,林名驰,谢力. 基于成本估算风险的武器装备激励价格合同模式[J]. 装甲兵工程学院学报,2018,32(1): 33—37. [11] 孙胜祥,韩霜. 基于双层决策的装备订购多因素激励定价模型与算法[J]. 系统工程与电子技术,2020,42(6): 1338—1347. [12] 徐哲. 武器装备项目进度、费用与风险管理[M]. 北京: 国防工业出版社, 2011: 31—33. [13] 吕建伟, 陈霖, 郭庆华. 武器装备研制的风险分析与风险管理[M]. 北京: 国防工业出版社, 2005: 80—81.
计量
- 文章访问数: 141
- HTML全文浏览量: 76
- PDF下载量: 8




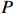
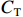

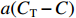
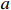
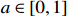
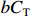


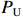
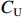
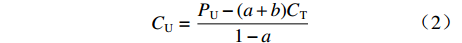
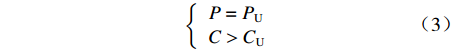

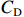
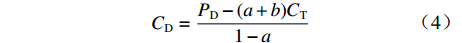
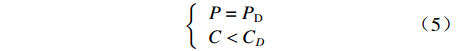
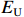
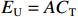
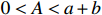
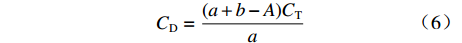
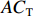
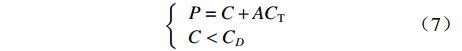
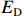
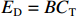
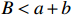
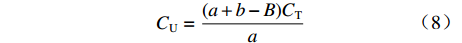

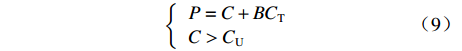
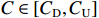
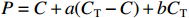

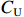
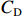
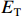

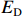

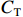
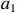

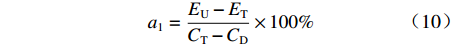



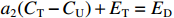
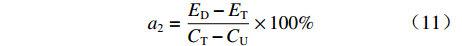
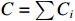


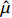

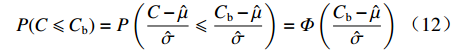
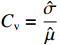

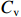
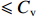
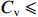
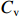



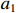
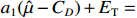

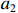
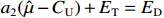

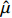
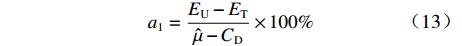

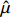
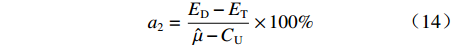
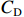
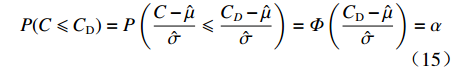
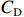
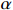
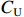
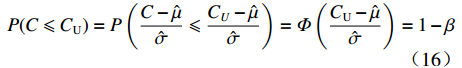
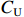
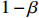
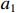


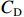
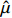
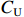
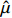
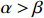
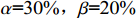
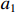
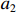
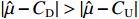
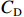

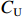

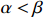
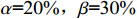

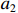
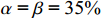
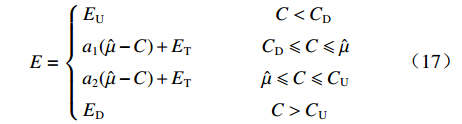

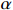
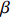

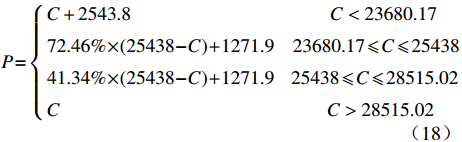
 下载:
下载:
