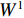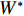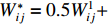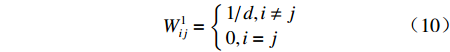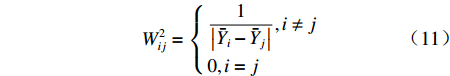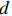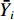Intelligent Manufacturing, Environmental Pollution and Labor Price Distortion
-
摘要:
改善劳动力要素价格扭曲是提升全要素生产率和实现高质量就业的重要突破口,智能制造打破原有劳动力高位扭曲的端倪初显。基于2006—2020年30个省(自治区、直辖市)的面板数据,先是系统性梳理了智能制造和环境污染影响劳动力价格扭曲的作用机制,再是综合运用双向固定效应模型、广义空间两阶段最小二乘法和交互固定效应模型验证了智能制造和环境污染对劳动力价格扭曲的影响效应。研究结果表明,智能制造能显著缓解劳动力价格扭曲,这一结论再经过一系列稳健性检验后依然成立;环境污染在智能制造减缓劳动力价格扭曲的传导过程中发挥着部分中介效应,即环境污染本身不会缓解劳动力价格扭曲,但它强化了智能制造的减缓作用。现阶段,智能制造主要通过减少二氧化碳排放量的中介缓解劳动力价格扭曲。
Abstract:Improving the price distortion of labor factors is an important breakthrough to improve total factor productivity and achieve high-quality employment. Intelligent manufacturing has broken the original high distortion of labor force. Based on the panel data of 30 provinces from 2006 to 2020, the first systemic combed the intelligent manufacturing and environmental pollution affect the mechanism of action of labor price distortion, then the integrated use of the bidirectional fixed effects model, two-stage least squares method and generalized space interaction fixed effects model of intelligent manufacturing and environmental pollution is verified labor price distortion effect. The results show that intelligent manufacturing can significantly alleviate labor price distortion, and this conclusion still holds after a series of robustness tests. Environmental pollution plays a partial intermediary effect in intelligent manufacturing to mitigate the transmission of labor price distortion, that is, environmental pollution itself does not mitigate labor price distortion, but it intensifies the moderating effect of intelligent manufacturing. At present, smart manufacturing alleviates labor price distortions mainly through the intermediary of reducing carbon dioxide emissions.
-
一、 问题的提出
自1992年中国逐步开启对资源分配机制进行市场化改革以来,要素市场分配机制已缓慢转向市场供需决定机制,形成了较为健全的商品市场机制。但由于产业政策、市场分割和制度障碍等“经济楔子”影响,中国要素市场的市场化改革还道阻且长。尤其是生产要素价格的决定机制,关键要素的控制权和定价权仍由各级地方政府掌控,使得要素价格难以有效发挥对市场配置机制的调节作用,以劳动力和资本为代表的要素价格扭曲普遍存在[1]。受限于城乡二元结构,中国劳动力价格扭曲还较为严重,且其积极效应正在急速衰减:一方面,由劳动力价格扭曲形成的人口红利,随着老龄化加剧和用工成本上升正在消失;另一方面,虽然劳动力要素价格扭曲为国际出口创造的价格比较优势有助于贸易顺差,但其本质是将原属于本国劳动要素的收入转化为对进口国的补贴,据此形成的贸易竞争力实质上是一种国民福利的损失[2]。我国要素市场价格扭曲的形成有其独特的历史缘由,但世界上大多数国家在经济起飞阶段都有可能会出现这样的市场状态,因为这个阶段,仅仅是依靠市场力量是难以将珍贵的生产要素配置到国民经济生产亟需的部门和行业,尤其是对于中国这样经济差异、区域差异和自然禀赋差异都比较大的国家。沿袭李斯特的幼稚产业保护理论来看,在经济发展初期,政府有形之手对市场做行政干预有其必要性和合理性。然而,尽管短期内要素价格扭曲有助于新兴产业茁壮成长和形成比较优势,但是长期扭曲的要素价格会抑制总需求进而导致供需失衡,最终使得宏观经济运行失衡。一个鲜明例子就是,劳动力价格扭曲会抑制资源的有效配置,进而抑制绿色经济效率和全要素生产率,这无形中拖累了中国迈向高质量发展的步伐[3]。因而总体来看,被扭曲的劳动力价格终究是没有生命力的,是不可持续的[4]。2022年国务院办公厅《要素市场化配置综合改革试点总体方案》[5]明确指出,要推动要素市场化配置改革纵深发展,着力破除阻碍要素自主有序流动的体制机制障碍,为完善要素市场制度、推动经济高质量发展提供强劲动力。
随着智能机器变得更加强大和广泛使用,这为市场体系的基础特征带来了全新挑战,即大多人依靠出售劳动来获取收入将面临更加严苛的挑战。2020年6月第三代生成预训练转换器(Generative Pretrained Transformer-3,GTP-3)的问世,意味着人工智能可以开始自行编写代码,并能模仿人类熟练使用语言和词汇,人工智能开始进入“无所不能”的领域。文本机器人GPT-3等人工智能的产生与应用,代表了以大数据和人工智能为基础的数字技术全面兴起,也标志着人类社会已步入以大数据、云计算和深度学习等技术为核心生产力的数字经济时代。在这个时代,人工智能推动的“技术奇点”正逐步超越所有人类智慧和人脑的计算能力,进而推动人类社会爆发式发展。现阶段,人工智能技术在语音语义识别、自然语义识别、文本生成、深度学习和红外传感等方面取得实质性突破,相较于工业革命时代的技术进步,数字经济时代的人工智能具有显著的自主学习型、进化性、群体性和交互性等人类特征,对人类社会的生产生活有更强的穿透性和颠覆性。技术是生产率与经济增长的主要动力,是繁荣的源泉,但计算机信息技术和数字革命技术在经济社会发展中还是社会不平性的重要驱动因子[6]。相关研究表明,人工智能和智能制造技术已不经意间扩散到各个产业部门并渗透于企业内部组织管理和经营决策,这必将引发人类社会劳动雇佣关系的重大变革[7]。因此,从以智能制造为代表的人工智能技术角度来探讨其对要素市场的影响对于纠正价格扭曲,以及如何进一步巩固市场在资源配置中起决定作用有启示意义。
纵观现有文献,与本文相关的话题大致可以分为两个方面。一是劳动力价格扭曲的测算和区域差异研究[8-10];二是从外商直接投资[11]、国际市场疲软[12]、市场分割[13]和高校扩招[14]等视角对劳动力价格扭曲的影响进行探讨。但是关于技术进步、人工智能技术和智能制造如何影响中国劳动力价格扭曲,以往研究并没有形成一个完整的理论体系,也还未回答其有何作用。因此,在数字经济现实背景下,揭示智能制造影响劳动力价格扭曲的一般规律,回答智能制造对劳动力要素市场化改革究竟是福还是祸,厘清智能制造推动劳动力优化配置的内在机制,这对于深入挖掘数字技术赋能经济高质量发展的潜力,扭转要素价格扭曲有启示性。
二、 研究假设
(一) 智能制造与劳动力价格扭曲
技术创新和科技创新会影响劳动和资本的边际产出率,并最终影响劳动者的产出收入比[15]。在数字经济时代,继大数据和人工智能成为生产要素之后,社会生产活动的效率得到极大提升,生产要素之间的融合与联系变得前所未有的紧密,经济增长乏力的趋势也将有望随之得到缓解。与此同时,供给侧结构性创新和变革反过来又会促进需求的扩张和提升,具体表现为知识经济的崛起、产品种类的增长以及质量的提升[16]。智能制造作为新一代通用目信息技术,其天然携带一般ICT所具备的渗透性、替代性和协同性等经济技术特征,不经意间已深入要素市场,并重构着劳动供需版图。从短期来看,智能制造系统在生产领域大规模安装使用,客观上提高了资本有机构成,放大了资本要素的产出贡献,间接促使劳动密集型企业向资本密集型企业转型。但这也意味着,智能制造挤占了劳动要素投入份额。智能制造释放的巨大生产力缩短了单个任务的工作时间,部分常规性、重复性工作岗位将被取代。与此同时,智能制造对就业的破坏效应,在一定程度上迫使劳动者提高劳动技能和注重人力资本积累。传统体力劳动者和低技能劳动者将会在时代进步的洪流中被替代,这无形中会改变劳动者的工作内容和工作效率[17]。从长期来看,随着数字经济的纵深发展,以往被数字化技术和自动化技术替代的劳动者可以通过就业灵活化和平台化实现转移再就业,越来越多的劳动者选择电商客服、外卖配送和视频直播的方式就业,这些新兴行业往往能带来较高的工资收入。因而智能制造可以直接增加自动化行业中技术工人的效率工资,还能通过更加细化的劳动分工使被替代的劳动者在新兴行业中实现再就业,进而矫正劳动力价格扭曲。据此提出:
假设1. 智能制造通过补偿效应和创新效应促进再就业,从而缓解劳动力价格错配。
(二) 环境污染与劳动力价格扭曲
环境污染加速了健康人力资本的折旧和居民生活福利的损失。长期暴露于细颗粒物的环境中已被认为是导致心血管疾病死亡率较高的主要原因之一,空气中高浓度的PM2.5和PM10会随着人类呼吸行为深入肺部诱发呼吸道和心血管疾病。因此环境恶化最直接的结果是诱发呼吸系统、消化系统和心血管系统等生理疾病,甚至是引致新生婴儿发病率高和成年人过早死亡。在中国,淮河以北集中供暖政策致使总悬浮颗粒物(TSPs)浓度创下184μg/m3的历史新高,由此导致人均预期寿命直接减少5.5年[18]。空气污染除了威胁居民健康之外,还对广大群众的户外活动、消费行为、工作效率和情感情绪等方面都有着不利影响[19]。在严重环境污染情形下,人们会不由自主地采取主动避让行为,减少户外出行和加强防护。由于环境污染与大脑的氧化应激直接相关,对于那些长期暴露于雾霾的户外工作者,其个体工作效率和注意力通常会因为空气污染而大打折扣。总体来看,环境污染无疑会在一定程度上耗损社会有效劳动力供给和城市活力。在环境污染系数较高地区工作的居民应得到较高的工资收入以平滑健康成本支出,即企业应当充分承担环境污染的负外部性成本。而企业出于利润最大化考量,一般不会主动承担环境污染的负外部性成本。因此,环境污染不仅增加了劳动者的健康成本,还降低了生产效率,出现高污染和低工资并存的现象,这加剧了动力价格扭曲[20]。据此提出:
假设2. 环境污染会加剧劳动力价格扭曲。
(三) 智能制造对环境污染的影响
人工智能制造、算法和工业机器人等属于高新技术,在生产过程中衍生的人机协同工作岗位增加企业对高技能、高知识劳动力的需求,最终表现为更高的劳动边际生产效率[21]。这些均能在一定程度上降低企业在资本和土地等有形生产要素的投入,同时还能借助高生产效率获取更高的劳动产出,进而提高绿色全要素生产率。作为通用目的人工智能技术能够促进创新互补,往往比单一的技术产品更具潜在价值,能够应用到生产的各个环节和领域,从而改变经济运行模式。凭借智能制造先进的智能监控系统和外红感知技术,企业在生产过程中能很快地锁定污染源,从而实现污染控制由末端治理转向源头治理。伴随着公众对良好生态环境向往的追求增加和人们环保意识增强,工业企业囿于维护自身形象和社会信誉的考虑,会相应的增加资金投入以引进或研发绿色技术,实现“末端污染治理”向“源头治理”转变,从而取得先发优势,占据市场有利地位。据此提出:
假设3. 智能制造可以提高环境质量,从而缓解劳动力价格错配。
三、 研究设计
(一) 变量说明
1. 劳动力价格扭曲
在完全竞争市场中,企业在生产规模不变的情形下展开生产,此时耗竭性分配效应占据主导:每单位劳动力要素所获得的资本报酬是与其边际产出是等价的,所有产出价值刚好被分配完毕,因而在完全竞争市场环境中是不存在工资扭曲的[22]。但在实际经济运行过程中,由于宏观制度、交易成本和信息不充分等因素干扰,市场竞争是不充分的,劳动力要素价格与其边际产出往往存在一定程度的偏离,工资扭曲是普遍存在的。基于此概念,可以得到劳动力价格扭曲程度主要是通过计算劳动力实际价格与其边际产出的比值得到。延续王少国和孙哲[23]的思路,在C-D生产函数的基础上使用随机前沿估计法(SFA)来推导劳动力的边际产出
$ MPL $ 。函数具体表现形式为:$$ \ln {Y_{it}} = {\alpha _0} + {\alpha _1}\ln {K_{it}} + {\alpha _2}ln{L_{it}} + {\nu _{it}} - {\mu _{it}} $$ (1) 式中,下标
$ i $ 和$ t $ 分别表示省份和年份,$ K $ 和$ L $ 分别表示资本投入和劳动力投入,$ Y $ 表示以2006年为基期的实际产出。$ {\nu _{it}} - {\mu _{it}} $ 表示复合误差项,其中$ {\nu _{it}} $ 为服从白噪声过程中的随机扰动项,反映了不可控因素对模型估计造成的偏误问题;$ {\mu _{it}} $ 为单边误差项,反应的是非技术效率。由式(1)可得到劳动力的边际产出弹性为:$$ MP{L_{it}} = \frac{{\partial {Y_{it}}}}{{\partial {L_{it}}}} = \frac{{{Y_{it}}}}{{{L_{it}}}}\frac{{\partial {Y_{it}}}}{{\partial \ln {l_{it}}}} = {\alpha _2} \times \frac{Y}{L} $$ (2) 因而劳动力价格扭曲指数表示为:
$$ dist{l_{it}} = \frac{{MP{L_{it}}}}{{Wag{e_{it}}}} $$ (3) 式中,
$ distl $ 表示劳动力价格扭曲。当$ distl = 1 $ 时,表明不存在劳动力价格扭曲;当$ distl \prec 1 $ 时,表示劳动力的实际工资高于市场均衡时产品的价值,劳动力价格被某些因素拔高了,存在向上扭曲;当$ distl \succ 1 $ 时,表示劳动力的实际工资低于市场均衡时产品的价值,劳动力价格被某些外在因素给压低了,存在一个向下的扭曲。$ Wage $ 表示实际工资,本文选取城镇单位就业人员总工资进行表征,并采用居民消费指数以2006年为基期做平滑处理。2. 智能制造
现阶段用于衡量人工智能或智能制造发展程度的做法主要有两种:一是采用信息传输、计算机服务和软件业全社会固定资产投资占国民生产总值的份额作为代理变量[24],二是采用工业机器人安装密度或渗透度(单位劳动力所对应的工业机器人数量)作为代理变量[25]。有别于蒸汽时代的“第一次机器革命”,自动化、数字化和智能化已成为“第二次机器革命”最重要的特征标签,技术进步已不再是仅以增强人类劳动效果为方向,而是更多地呈现出对人类劳动的替代。根据此定义,本文采用工业机器人安装密度表征智能制造。国际机器人联盟(IFR)从2006年开始提供较为详细的分行业工业机器人安装数量,但是其仍公布的是国家层面的数据,省级工业机器人的安装数量还未可知。对此,参照闫雪凌等[26]、王永钦和董雯[27]的研究思路,采用巴蒂克工具变量法计算各省份工业机器人安装数量。具体而言,先是根据《中国劳动统计年鉴》《中国工业统计年鉴》等数据源提供的制造业二位码行业就业数据,然后利用IFR所提供的全球分行业工业机器人数据中所涉及的14个制造业子行业,根据行业分类标准、属性和名称与中国31个制造业子行业进行匹配。其具体计算公式为:
$$ Ro{b_{it}} = \sum\limits_{j = 1}^J {\frac{{{L_{jit}}}}{{{L_{it}}}} \times \frac{{Ro{b_{jt}}}}{{{L_{jt}}}}} \times \frac{{MRo{b_t}}}{{{L_{2005}}}} $$ (4) 式中,Rob表示工业机器人安装密度,
$ {L_{jit}} $ 为$ i $ 省份$ j $ 行业$ t $ 年的从业人员数量,$ {L_{it}} $ 表示$ i $ 省份$ t $ 年就业人员总量,$ Ro{b_{jt}} $ 表示$ j $ 行业$ t $ 年的工业机器人安装数量,$ {L_{it}} $ 为$ j $ 行业$ t $ 年的从业人员总量;$ {{MRo{b_t}} \mathord{\left/ {\vphantom {{MRo{b_t}} {{L_{2005}}}}} \right. } {{L_{2005}}}} $ 为本文选取的工具变量,其中$ MRo{b_t} $ 表示美国在年份$ t $ 的工业机器人安装数量,$ {L_{2005}} $ 表示2005年美国制造业从业人员数量。3. 环境污染
现阶段,气候暖化已成农业、工业、海岸带甚至是人类社会可持续发展带来了严重威胁。2021年3月公布的“十四五”规划与2035远景目标中明晰了今后一段时间内环境治理的新方向和重点领域,将碳达峰、碳中和目标上升到国家发展的战略高度。践行“双碳”目标须打破环境(大气污染物)和气候(温室气体)的界限,将减污降碳协同增效作为未来工作的重中之重。可以明确的是,在“双碳”大背景下,如何减少企业和消费者碳排放行为,将是未来一段时间内生态文明建设和环境保护的目标导向。基于此,本文选取单位生产总值终端碳排放量作为代理变量。省级层面的碳排放量参考联合国气候变化专门委员会在2006年公布的碳排放核算公式进行计算,其包含了煤炭、焦炭、原油、汽油、煤油、柴油、天然气和燃料油八类能源的终端消费量,具体核算公式为:
$$ C{O_2} = \frac{{44}}{{12}} \times \sum\limits_{K = 1}^8 {C{O_k}} \times N{C_k} \times E{F_k} \times {O_k} $$ (5) 式中,k表示化石能源类型;
$ CO $ 、$ NC $ 、$ EF $ 、$ O $ 分别表示化石能源的消耗量、平均低位热值、单位热值含碳量和碳氧化率。唐贵谦等[28]指出大气污染与温室气体有着极强的同源性,两者与化石燃料的燃烧和使用密切相关。考虑到模型稳健性,本文还选取了工业二氧化硫排放量作为第二个环境污染的代理变量。4.控制变量
因影响劳动力价格扭曲的因素有很多,为尽可能缓解遗漏重要变量对模型估计造成的偏误问题,本文还选取了6个外部变量对模型进行控制。具体而言:外商直接投资(FDI),选用各省份实际利用外商直接投资额作为代理变量;劳动供给(lab),选取人口自然增长率作为代理变量;工业化率(IR),选取第二产业产值占总产值的比重进行表征;宏观调控(Gov),选取地方财政一般预算支出占国内生产总值的比重进行表征。最低工资(Min),选取各省份下辖的各地级市所制定的最低工资标准方案中的最高档月工资标准作为代理变量;创新创业(Start),选取每年新增的创业公司数量作为代理变量。
(二) 构建计量模型
文章意在验证智能制造对劳动力价格扭曲的影响,以及环境污染在其传导过程中发挥着何种中介效应。根据上文对各变量的选取和确定,先是构建智能制造影响劳动力价格扭曲的计量模型:
$$ dist{l_{it}} = {a_0} + {a_1}LnI{M_{it}} + {a_2}{Z_{ijt}} + {\mu _i} + {\nu _t} + {\varepsilon _{it}} $$ (6) 式中,
$ {\mu _i} $ 表示个体固定效应,$ {\nu _t} $ 表示时间固定效应,$ \varepsilon $ 表示随机扰动项,$ a $ 表示估计参数;$ Z $ 表示信息集,包含所有控制变量。进一步地,沿袭温忠麟等[29]的思路,构建智能制造、环境污染和劳动力价格扭曲的中介效应检验方程组。需要说明的是,尽管近年来三段式的中介效应检验方法饱受质疑,究其根本是该方法“巧合式”的统计推断不符合经济学严谨的因果推断,中介效应的成立条件依赖于变量间巧合的线性回归关系。从底层逻辑来看,该方法最大的缺陷在于无法解决三个变量间的内生性问题。本着能用但是慎用的原则,文章将中介效应检验部分的面板数据拟合模型转化为面板交互固定效应模型(Interactive Fixed Effect)。该模型充分考虑了现实经济中存在的多维冲击问题,以及不同个体对这些冲击力度所表现出的异质性反应,在控制遗漏变量、捕捉时变特征和提高拟合优度等方面有明显优势,是面板数据研究较为活跃的研究前沿之一[30]。因此将式(6)转化为以下交互固定效应模型:$$ dist{l_{it}} + {\beta _0} + {\beta _1}LnL{M_{it}} + {\beta _2}{Z_{ijt}} + {\lambda '_i}{F_t} + {\mu _i} + {\nu _t} + {\varepsilon _{it}} $$ (7) 式中,
$ {\lambda '_i}{F_t} $ 为交互固定效应,表示多维个体效应与多维时间效应的乘积;$ {F_t} $ 为共同因子,$ {\lambda _i} $ 为因子载荷。在实际操作过程中,文章假定模型存在两个共同因子,即$ {\lambda '_i}{F_t} = {\alpha _i} + {\xi _t} $ 。进一步的,再构建两个方程式来组成中介效应检验程序:$$ Pol{l_{it}} = {c_0} + {c_1}LnI{M_{it}} + {c_2}{Z_{ijt}} + {\lambda '_i}{F_t} + {\mu _i} + {\nu _t} + {\varepsilon _{it}} $$ (8) $$ dist{l_{it}} = {d_0} + {d_1}LnI{M_{it}} + {d_2}Lnpol{l_{it}} + {d_3}{Z_{ijt}} + {\lambda '_i}{F_t} + {\mu _i} + {\nu _t} + {\varepsilon _{it}} $$ (9) 式(7)至式(9)共同组成中介效应递推方程组。式(7)测算的是核心解释变量对被解释变量的总效应
$ c $ ,其显著是中介效应存在的基本前提,若$ c $ 不显著,那么就没有必要展开后续的中介效应检验程序。式(9)表示分离环境污染后的间接效应后智能制造对劳动力价格错配的直接效应$ c' $ ;式(8)表示智能制造对环境污染的直接影响,其与式(9)中环境污染的估计系数乘积共同构成间接效应,即$ {\beta _1} \times {\varphi _2}{\text{ = }}ab $ 。在各变量都标准化的情况下一定存在$ c = c' + ab $ ,即直接效应和间接效应之和等于总效应。在实际拟合过程中,为了减缓异方差干扰,本文对部分数值较大的变量进行了对数化处理。(三) 数据来源
遵循数据可得性和可比性原则,选取2006—2020年中国30个省(自治区、直辖市)的样本数据(不含西藏和港澳台)。工业机器人的数据来源于国际机器人联盟,其余指标的原始数据主要来源于《中国统计年鉴》《中国工业统计年鉴》《中国人口和就业统计年鉴》、EPS数据库和中国研究数据服务平台(CNRDS)。2005年美国制造业从业人员数量数据来自于美国经济分析局(U.S. Bureau of Economic Analysis)。极少数缺失值使用线性插值法补齐。
四、 实证分析
(一) 基准回归
考虑到计量模型的随机扰动项很难满足同方差、无自相关和无截面相关的经典假定,若忽视这三个问题,估计结果往往是有偏和不一致的。对此,本文采用Driscoll-Kraay标准误予以应对。表1报告的是智能制造影响劳动力价格扭曲的估计结果。出于稳健性考虑,文章还报告了混合最小二乘法和未加入任何控制变量时的估计结果。
表 1 基准回归结果变量 POLS POLS FE FE FE IM −0.354***
(−546)−0.713***
(−4.34)−0.378***
(−12.34)−0.143
(−1.18)−1.036***
(−6.51)FDI 1.345***
(5.94)0.253
(1.32)−0.180
(−1.22)Gov 0.084***
(3.54)0.040**
(2.55)0.031**
(2.28)IR 0.051***
(3.72)0.029*
(2.57)0.083***
(3.66)Min 0.001
(1.17)−0.003***
(-7.81)−0.005***
(−3.87)Start −1.084***
(-4.71)1.154***
(5.04)0.622**
(2.83)Lab −0.184***
(−5.22)−0.107
(−1.49)−0.074
(−1.12)常数项 4.043***
(14.07)−0.118
(−0.04)4.120***
(40.01)−12.270***
(−3.33)−3.152
(−0.80)个体效应 NO NO YES YES YES 年份效应 NO NO NO NO YES R2 0.4781 0.3658 0.2825 0.3823 0.4458 注:***、**、*分别表示在1%、5%和10%显著性水平上显著,括号内报告的是t统计量,以下各表同。 由表1可知,在仅考虑智能制造影响劳动力价格扭曲的情形下,智能制造的估计系数为−0.354且在1%水平下显著;再从考虑了控制变量、时间效应和个体效应的估计结果来看,智能制造的估计系数为−1.036且在1%水平下显著。混合最小二乘法与双向固定效应模型的估计结果均显示显著的负向关系这表明智能制造能缓解劳动力价格扭曲,认为智能制造能显著缓解劳动力价格扭曲,只是两者估计系数有差异,这表明智能制造缓解劳动力价格扭曲的结论是稳健和可靠的。伴随着人工智能技术在国民各个领域、地区、行业以及部门的广泛渗透和扩散,新技术的发展显著改善了国民就业和劳动力结构,不同程度的技能溢价日渐凸显,人力资本需求逐渐由中低技能演化至高技能,非程序性岗位的劳动力需求不断增加,原本任务性工作岗位的劳动力则会在更深层次劳动分工体系中创造劳动价值。可以明确的是,以工业机器人为代表的智能制造,在替代原本因由中低端劳动力执行的工作任务同时,其所释放的巨大生产力,还能通过降低生产成本和扩大市场份额的方式增加了对其他劳动密集型产品的劳动力需求。新技术降低了提供灵活劳动力就业的交易成本,使非接触经济、零工经济和协同众包等劳动方式成为可能,以往那些只能从事传统制造的工业可以流入生产性服务业或新兴行业等部门,这推动了劳动力要素在更大范围内的产业部门中实现转移和再配置,在有限的市场份额中扩大了竞争通道,这有助于提高整个社会的均衡工资和效率工资,进而缓解劳动力价格扭曲。
(二) 稳健性检验
上文基准回归结果证实了智能制造能显著缓解劳动力价格扭曲,但双向固定效应模型未考虑智能制造与劳动力价格之间的双向因果内生关系。事实上,微观市场经济运行时无时无刻不面临着要素配置问题,即如何将稀缺的土地、劳动力、资本和企业家才能等要素用在最具“生产力”的地方。一旦市场中不存在阻碍要素自由流动的障碍因子,那么整个社会的福利水平将会达到前所未有的高度。然而,要素价格扭曲会使得资源配置陷入低效率状态,整体经济的运行效率无法充分发挥,经济体中很有可能出现长期产出不足与失业率升高并存的现象。劳动力价格扭曲意味着部分地区工资水平低于均衡值,尽管较低的用工成本对外部企业入驻投资有极大吸引力,尤其是对于劳动密集型。但不能忽视的是,低工资水平往往意味着高端人才供给不足,这种低端劳动力供给模式决定了企业的技术创新路线是,更多地使用有形生产要素而降低知识和经验等无形生产要素在生产活动中的比重[31]。但从另一方面来看,劳动力要素价格扭曲还会倒逼企业改革创新。既然城市内部在发展资金和高端人才两方面处于劣势,那么低水平无效率的企业很容易被激烈的市场竞争淘汰。为避免这一情况的发生,企业在其能力范围内引进自动化办公模式以弥补优质劳动力供给不足。因此,劳动力价格错配会拉低城市工资,有利于劳动密集型企业发展,但不利于工厂自动化和智能制造转型。因此,智能制造与劳动力价格扭曲之间存在千丝万缕的反向因果关系。
为消除智能制造与劳动力价格扭曲之间的内生关系,参照沈洋等[32]的做法,将空间计量模型中各解释变量及其3阶空间滞后项的交互项作为工具变量,在基于两阶段最小二乘法(2SLS)建立广义空间两阶段最小二乘法(GS2SLS)和广义空间自回归两阶段最小二乘法(GS2SLSAR)来同时控制变量间的空间相关性和互为因果内生性问题,从而保证模型参数估计的无偏性和一致性。此外,本文还在动态空间面板模型中纳入广义矩估计模型(GMM)。将变量的时间滞后项和空间滞后项作为工具变量,从而建立起空间面板系统矩估计模型(SPGMM),这也能消除空间计量模型中的内生性问题。为了更为全面地刻画省份间的地理距离和经济差距信息,空间权重矩阵采用各省份省会城市间的地理距离
$ {W^1} $ 和各省份2006—2020年人均生产总值差值的倒数$ {W^2} $ 来构建经济地理嵌套矩阵$ {W^*} $ ,其计算公式为$ W_{ij}^* = 0.5W_{ij}^1 + 0.5W_{ij}^2 $ 。同时考虑到空间计量模型受空间权重矩阵影响较大,本文还构建了地理邻接矩阵作为对照。经济矩阵和邻接矩阵的构造方程见式(10)和式(11):$$ W_{ij}^1 = \left\{ \begin{gathered} {1 \mathord{\left/ {\vphantom {1 {d,i \ne j}}} \right. } {d,i \ne j}} \\ 0,i = j \\ \end{gathered} \right. $$ (10) $$ W_{ij}^2 = \left\{ \begin{gathered} \frac{1}{{\left| {{{\bar Y}_i} - {{\bar Y}_j}} \right|}},i \ne j \\ 0,i = j \\ \end{gathered} \right. $$ (11) 式中,
$ d $ 表示两省份省会城市间的地理距离;$ {\bar Y_i} $ 表示$ i $ 地区2006—2020年人均生产总值的均值。由表2可知,考虑智能制造与劳动力价格扭曲间的双向内生关系后,三个空间计量模型均显示至少在10%显著性水平上认为智能制造能缓解劳动力价格错配的结论是成立的。尽管在嵌套矩阵中GS2SLS和GS2SLSAR模型的显著性有所降低,但仍在可接受范围内,可以证明基准回归结果是稳定的。同时在邻接矩阵中可以发现三个空间计量模型的估计结果与嵌套矩阵的结果类似,显著性还有所提高,这更加佐证了基准回归模型的稳定性。
表 2 稳健性检验变量 嵌套矩阵 邻接矩阵 GS2SLS SPGMM GS2SLSAR GS2SLS SPGMM GS2SLSAR IM −0.372**
(−2.21)−0.654***
(−4.44)−0.305***
(−2.78)−0.313**
(−2.50)−0.629***
(−4.96)−0.573***
(−5.45)控制变量 Yes Yes Yes Yes Yes Yes 常数项 −9.162***
(−2.64)2.259
(−0.09)−8.289***
(−2.81)−8.684***
(−2.62)2.095
(0.86)−0.032
(−0.53)五、 中介机制检验
在上文理论分析部分,文章认为环境污染会增加劳动者健康成本和降低生产效率,从而加剧劳动力价格扭曲。而智能制造有助于企业精准识别污染源和提高要素产出效率,进而提高绿色全要素生产率,实现劳动力价格扭曲减缓。为验证研究假设2和假设3,依据式(7)至式(9)构建的中介效应递推方程式进行检验。
由表3可知,智能制造对二氧化碳和工业二氧化硫排放量的估计系数分别是−0.062和−0.133,且至少在10%水平下显著,该结果表明智能制造能改善环境质量的直接效应是成立的。再从第4列和第6列的结果来看,智能制造的估计系数分别为−0.874和−0.678,加入二氧化碳的模型结果相较于总效应的估计系数有所提升;其中二氧化碳和工业二氧化硫排放量的估计系数分别为0.660和0.187,且这两个变量至少在5%的显著性水平上显著,表明递推方程的间接效应成立。最后从符号角度来看,可以发现间接效应与总效应的符号保持一致,环境污染呈现出部分中介作用,验证了研究假设2和假设3。二氧化碳和工业二氧化硫的中介效应占比分别为5.81%和3.52%,即现阶段智能制造主要通过减少二氧化碳排放量的中介渠道来改善劳动力价格扭曲。
表 3 中介效应检验结果变量 distl CO2 distl SO2 distl IM −0.706**
(−2.34)−0.062*
(−1.95)−0.874***
(−3.88)−0.133***
(−2.56)−0.678***
(−2.99)CO2 0.660***
(2.89)SO2 0.187**
(2.16)控制变量 Yes Yes Yes Yes Yes 个体效应 Yes Yes Yes Yes Yes 年份效应 Yes Yes Yes Yes Yes 六、 结论与启示
以智能制造为代表的自动化技术正深刻影响劳动力供需版图,对经济高质量发展和民生就业有重大影响。文章先是从理论逻辑层面系统性梳理了智能制造和环境污染对劳动力价格扭曲的影响;再是结合中国2006—2020年30个省份的面板数据,综合运用固定效应模型、交互固定效应模型和广义空间两阶段最小二乘法等数理统计模型验证了智能制造对劳动力价格扭曲的影响效应,以及在其传导过程中环境污染发挥着何种中介作用。笔者主要的研究结论和发现主要在于以下两个方面:
第一,智能制造能显著减缓劳动力价格扭曲,且这一结论再考虑内生性问题后依然成立;环境污染主要通过增加劳动者健康成本和降低生产效率的方式加剧劳动力错配。
第二,在智能制造减缓劳动力价格扭曲的传导过程中,环境污染发挥着部分中介效应,即环境污染本身污染缓解劳动力价格扭曲,但其强化了智能制造对劳动力价格的配置作用;现阶段,智能制造主要通过帮助企业减少要素投入和提高能源利用效率的机制渠道,从而减少二氧化碳排放量来强化其对劳动力价格扭曲的缓解作用。
对此,为发挥智能制造对劳动力价格错配的减缓作用,可以从以下几个方面着手:一是加快推进数字赋能传统产业升级,积极谋划工业设备和业务系统“上云上平台”。二是主动深化智能制造实施,加速推进“芯屏器核网”全产业链补链强链。三是重视培养劳动者的综合能力尤其是数字素养等与职业相关的现代认知能力,提高人机协同合作效率。四是因势利导指引相关市场主体增加研发投入和提高自主创新能力,加强对环境友好型技术的开发、掌握和规模化应用。
-
表 1 基准回归结果
变量 POLS POLS FE FE FE IM −0.354***
(−546)−0.713***
(−4.34)−0.378***
(−12.34)−0.143
(−1.18)−1.036***
(−6.51)FDI 1.345***
(5.94)0.253
(1.32)−0.180
(−1.22)Gov 0.084***
(3.54)0.040**
(2.55)0.031**
(2.28)IR 0.051***
(3.72)0.029*
(2.57)0.083***
(3.66)Min 0.001
(1.17)−0.003***
(-7.81)−0.005***
(−3.87)Start −1.084***
(-4.71)1.154***
(5.04)0.622**
(2.83)Lab −0.184***
(−5.22)−0.107
(−1.49)−0.074
(−1.12)常数项 4.043***
(14.07)−0.118
(−0.04)4.120***
(40.01)−12.270***
(−3.33)−3.152
(−0.80)个体效应 NO NO YES YES YES 年份效应 NO NO NO NO YES R2 0.4781 0.3658 0.2825 0.3823 0.4458 注:***、**、*分别表示在1%、5%和10%显著性水平上显著,括号内报告的是t统计量,以下各表同。 表 2 稳健性检验
变量 嵌套矩阵 邻接矩阵 GS2SLS SPGMM GS2SLSAR GS2SLS SPGMM GS2SLSAR IM −0.372**
(−2.21)−0.654***
(−4.44)−0.305***
(−2.78)−0.313**
(−2.50)−0.629***
(−4.96)−0.573***
(−5.45)控制变量 Yes Yes Yes Yes Yes Yes 常数项 −9.162***
(−2.64)2.259
(−0.09)−8.289***
(−2.81)−8.684***
(−2.62)2.095
(0.86)−0.032
(−0.53)表 3 中介效应检验结果
变量 distl CO2 distl SO2 distl IM −0.706**
(−2.34)−0.062*
(−1.95)−0.874***
(−3.88)−0.133***
(−2.56)−0.678***
(−2.99)CO2 0.660***
(2.89)SO2 0.187**
(2.16)控制变量 Yes Yes Yes Yes Yes 个体效应 Yes Yes Yes Yes Yes 年份效应 Yes Yes Yes Yes Yes -
[1] 张杰,周晓艳,李勇. 要素市场扭曲抑制了中国企业R&D?[J]. 经济研究,2011,46(8):78—91. [2] 苏宏伟,刘莹. 劳动要素价格扭曲的区域差距、空间效应与动态演进[J]. 统计与决策,2021,37(19):53—56. [3] 张政,李雪松,王冲. 劳动力价格扭曲与绿色经济效率损失[J]. 云南财经大学学报,2020,36(4):51—63. [4] 许经勇. 劳动力均衡价格与劳动力价格扭曲[J]. 吉首大学学报(社会科学版),2007(5):14—17. [5] 新华网. 国务院办公厅印发《要素市场化配置综合改革试点总体方案》[EB/OL]. (2022-01-06)[2022-03-20]. http: //www.news.cn/politics/2022-01/06/c_1128238135.htm. [6] 希瑟·布西, 布拉德福德·德龙, 马歇尔·斯坦鲍姆. 皮凯蒂之后[M]. 余江, 高德胜, 译. 北京: 中信集团出版社, 2021. [7] 何勤,董晓雨,朱晓妹. 人工智能引发劳动关系变革:系统重构与治理框架[J]. 中国人力资源开发,2022,39(1):134—148. [8] 李言. 中国城市群生产要素价格扭曲比较分析[J]. 经济问题探索,2021(10):152—164. [9] 陈平,殷明明. 要素价格扭曲的测度及成因分析[J]. 金融学季刊,2017,11(3):20—54. [10] 李言,樊学瑞. 中国地区生产要素价格扭曲的演变:1978~2016年[J]. 数量经济技术经济研究,2020,37(1):62—82. [11] 安孟,张诚. 外资进入能改善中国的工资扭曲吗?——基于中国省级动态面板数据的实证研究[J]. 经济与管理研究,2019,40(8):63—75. [12] 陈晓华,刘慧. 外需疲软、生产技术革新与制造业劳动力价格扭曲[J]. 统计研究,2015,32(10):47—55. [13] 王鑫,齐秀琳,雷鸣. 工头制、劳动力市场分割与工资扭曲:来自近代工业的证据[J]. 南开经济研究,2018(5):115—132. [14] 蔡思远,陆军. 高校扩招能够改善工资扭曲吗?——来自中国工业企业的证据[J]. 当代经济科学,2021,43(4):131—142. [15] 许家云,张巍. 房价、要素市场扭曲与工业结构升级[J]. 财贸研究,2020,31(11):10—26. [16] 徐翔. 数字经济时代: 大数据与人工智能驱动新经济发展[M]. 北京: 人民出版社, 2021. [17] 明娟,卢小玲,胡嘉琪. 工业机器人应用对广东就业市场的影响研究[J]. 广东行政学院学报,2021,33(3):78—88. [18] HE J,LIU H,SALVO A. Severe air pollution and labor productivity:Evidence from industrial towns in China [J]. American Economic Journal:Applied Economics,2019,11(1):173—201.
[19] 魏下海,林涛,张宁,等. 无法呼吸的痛:雾霾对个体生产率的影响——来自中国职业足球运动员的微观证据[J]. 财经研究,2017,43(7):4—19. [20] 顾冉,蒲艳萍. 环境污染会加剧劳动力价格扭曲吗?——来自CFPS的微观证据[J]. 产业经济研究,2019(3):101—113. [21] 郭娅妮. 人工智能发展对我国绿色全要素生产率的影响——基于动态系统GMM估计和门槛模型的实证研究[J]. 河北农业大学学报(社会科学版),2021,23(5):29—37. [22] 魏下海,董志强. 城市商业制度环境影响劳动者工资扭曲吗?——基于世界银行和中国工业企业数据的经验研究[J]. 财经研究,2014,40(5):4—18. [23] 王少国,孙哲. 我国劳动要素价格扭曲测度及其因素分析[J]. 海派经济学,2021,19(4):152—165. [24] 沈洋,魏丹琪,周鹏飞. 数字经济、人工智能制造与劳动力错配[J]. 统计与决策,2022(3):28—33. [25] 芦婷婷,祝志勇. 人工智能是否会降低劳动收入份额——基于固定效应模型和面板分位数模型的检验[J]. 山西财经大学学报,2021,43(11):29—41. [26] 闫雪凌,朱博楷,马超. 工业机器人使用与制造业就业:来自中国的证据[J]. 统计研究,2020,37(1):74—87. [27] 王永钦,董雯. 机器人的兴起如何影响中国劳动力市场?——来自制造业上市公司的证据[J]. 经济研究,2020(10):159—175. [28] 唐贵谦,刘钰婷,高文康,等. 警惕大气污染和碳排放向西北迁移[J]. 中国科学院院刊,2022,37(2):230—237. [29] 温忠麟,叶宝娟. 中介效应分析:方法和模型发展[J]. 心理科学进展,2014,22(5):731—745. [30] BAI J. Panel data models with interactive fixed effects [J]. Econometrica,2009,77(4):1229—1279.
[31] 高帆. 中国农业生产率提高的优先序及政策选择[J]. 经济理论与经济管理,2008(8):12—19. [32] 沈洋,犹雨寒,周鹏飞. 数字普惠金融对新型城镇化的影响[J]. 金融与经济,2021(11):46—53.
计量
- 文章访问数: 154
- HTML全文浏览量: 70
- PDF下载量: 1



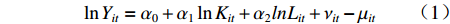

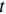
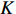
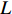
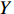

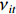
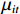
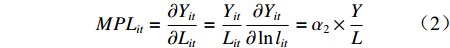
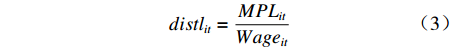
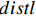

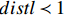
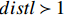
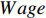
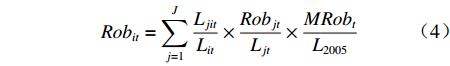


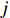
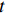
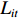

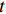
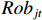
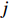
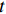
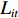
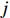



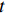
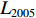
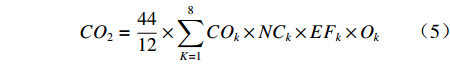
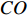
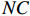
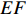

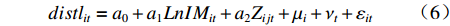
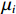

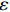
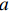

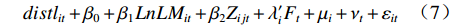
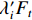

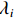
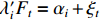
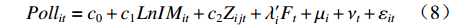
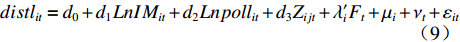
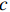

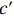
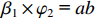

 下载:
下载: