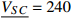Differential Game Study of Supply Chain under Carbon Tax Policy
-
摘要:
在碳税政策下,假设消费者需求受上下游企业碳减排量和低碳宣传努力程度的共同影响,考虑产品碳减排量受上游制造商碳减排努力程度影响的动态变化,构建成本分担前后制造商和零售商长期联合减排与低碳宣传的两种Stackelberg微分博弈模型。结果表明,与没有碳税相比,碳税政策的实施能够从长期角度提高产品的碳减排量和零售商的利润,但会降低制造商的利润;此外,当碳税税额与上下游企业边际利润满足一定条件时,成本分担契约能够进一步提高产品的碳减排量,实现上下游企业利润的Pareto改善,并拓宽碳税弹性空间。
Abstract:Under the carbon tax policy, it is assumed that consumer demand is jointly influenced by the carbon emission reduction levels of upstream and downstream enterprises and the efforts of low-carbon promotion. Two Stackelberg differential game models are constructed for the long-term joint emission reduction and low-carbon promotion of manufacturers and retailers before and after cost sharing, taking into account the dynamic changes of product carbon emission reduction influenced by the reduction efforts of upstream manufacturers’ emission. The results show that, compared with no carbon tax, the implementation of the carbon tax policy can improve the carbon emission reduction of products and retailers’ profits in the long run, but it will reduce manufacturers’ profits; in addition, when certain conditions are met regarding the carbon tax and the marginal profits of upstream and downstream enterprises, the cost-sharing contract can further improve the carbon emission reduction of products, achieve the Pareto improvement in profits of upstream and downstream enterprises, and broaden the elasticity space of the carbon tax.
-
一、 研究综述
随着全球气候变化情况日益严峻,温室气体排放问题受到世界各国政府的高度重视。2020年9月,习近平在第七十五届联合国大会一般性辩论上发表重要讲话:“二氧化碳排放力争于2030年前达到峰值,努力争取2060年前实现碳中和。”[1]目前,中国已构建和实施了“双碳”目标“1+N”政策体系,并超额完成2020年气候行动任务。英国、法国和加拿大等国家也纷纷作出气候承诺并出台各种不同的政策法规降碳减排,其中,碳税政策因其易操作性和有效性被各国政府广泛采用[2]。
当前,已有一些学者研究了碳税政策对供应链的单个成员企业或供应链的整个系统碳减排管理决策的影响。Bruvoll和Larsen应用一般均衡原理研究了碳税税率对碳排放量的影响,研究发现碳税在降碳减排方面作用明显[3];Petrakis和Poyago-Theotoky考虑企业碳减排创新水平对社会福利的影响,提出一个具有溢出效益的非锦标赛研发模型,并比较了不同碳税与碳减排补贴政策下的社会福利大小[4];Wesseh和Lin基于一般均衡模型分析了碳政策如何影响能源供应、福利和环境,结果表明,碳税政策的实施可以减少大约62.5%的环境污染[5];高举红等考虑不同碳政策下闭环供应链的定价决策,发现基于补贴和碳税的奖惩机制对降低碳排放量更有效[6];姜跃和韩水华在碳税规制下,考察了供应商参与制造商减排和零售商分担制造商减排成本契约对供应链成员最优碳减排决策和利润的影响[7];曹细玉和张杰芳面对随机市场需求,研究了当碳减排量一定时,碳税与碳减排创新补贴之间的变化关系[8]。从已有的研究成果可以看出,碳税政策对供应链的低碳化管理实践和成员利润均有很大影响,因此研究碳税政策下低碳供应链的运营管理问题是十分必要的。
在政府持续降碳减排的同时,消费者的低碳环保理念也在不断加强。Li等指出在缓解气变的巨大压力下,消费者越发关注供应链企业在绿色减排方面的表现[9];Loaiza-Ramirez等通过线性回归和非参数检验方法来考察消费者对绿色产品的关注度,研究发现消费者有更高的意愿购买绿色产品并为其支付溢价[10];朱庆华等基于消费者的低碳购买意愿,比较分析政府补贴给低碳产品制造商和低碳产品消费者两种情况下供应链成员的利润[11];孙嘉楠和肖忠东综合考虑消费者的低碳偏好和渠道偏好,研究低碳供应链的最优减排边界,并指出制造商可以通过低碳产品认证和广告宣传等方式提高消费者对低碳产品的认可度[12];孙立成等基于消费者的低碳偏好,研究供应链企业间碳排放转移对产品销售价和批发价的影响[13]。随着消费者低碳意识的形成和发展,消费者的低碳偏好已是供应链成员进行决策时所要考虑的重要因素之一。
此外,碳减排具有连续长期动态变化的特征,也引发一些学者的关注。徐春秋等首次从动态角度研究供应链企业上下游之间长期联合减排与低碳宣传问题,通过构建三种微分博弈模型分析供应链成员的最优减排决策及其利润大小[14]54-60;赵道致等基于碳减排的动态微分方程,考虑了零售商竞争对供应链成员利润的影响[15];刘名武等在碳交易和消费者具有低碳偏好的环境下,求解了制造企业碳排放和供应链利润的长期动态轨迹,并推导出实现双赢的低碳技术特征条件[16];Zhou和Ye研究了低碳环境下双渠道供应链中涉及一个制造商和一个零售商的微分博弈问题,结果表明消费者的零售渠道忠诚度对最优策略有重大影响[17];Zu等从动态变化的视角,分别以市场、政府和供应链为主要考虑因素研究了低碳供应链三种不同情况下的企业最优销售价格和减排决策[18]。然而,在动态视角下,研究碳税政策对供应链碳减排长期影响的文献还比较缺乏。到目前为止,仅有王君等在碳税规制背景下研究了制造商行为选择对碳排放和定价以及博弈双方利润的长期影响,结果表明制造商在考虑碳税的高低后会有不同的行为选择[19]。
笔者拟在碳税政策约束下建立成本分担前后两种Stackelberg微分博弈模型,进而研究碳税政策对供应链成员长期联合减排与低碳宣传以及利润产生的影响。研究的创新性主要体现在:首次在碳税政策约束下从动态视角研究供应链企业之间长期联合减排与低碳宣传问题,分析碳税对博弈双方的利润和低碳决策产生的长期作用,并考察碳税政策下成本分担契约在协调供应链绩效上的条件和拓宽碳税弹性空间上的效果。研究成果可以为政府碳税政策的制定和企业成本分担契约的选择提供科学依据和理论指导。
二、 问题描述与模型假设
(一) 问题描述
研究选择由进行碳减排的制造商和进行低碳宣传的零售商组成的二级供应链系统为研究对象,在碳税政策约束下研究供应链成员长期联合减排和低碳宣传的问题。在该问题中,制造商的碳减排努力程度直接影响低碳产品的碳减排量,而产品的碳减排量和零售商的低碳宣传努力程度又直接影响产品的市场需求。同时,为激励零售商加大低碳产品的宣传力度,制造商愿意为零售商分担部分低碳宣传成本。考虑到上游的制造商比下游的零售商面临更大的碳减排压力,研究选择制造商作为微分博弈的领导者,而零售商作为追随者,从而形成二者的Stackelberg微分博弈模型。双方的博弈决策过程如下:在碳税政策下,制造商首先确定自身的碳减排努力程度
$ {E_M}\left( t \right) $ 和为零售商分担的低碳宣传成本比例$ \phi (t) $ ;在观察到制造商的决策之后,零售商再决定自身的低碳宣传努力程度$ {E_R}\left( t \right) $ 。(二) 模型假设
假设1.
$$ {C_M}\left( {{E_M}(t)} \right) = \dfrac{1}{2}{k_M}E_M^2(t)$$ (1) $$ {C_R}\left( {{E_R}(t)} \right) = \dfrac{1}{2}{k_R}E_R^2(t)$$ (2) 式中:t表示时间,
${C_M}\left( {{E_M}(t)} \right) $ 表示制造商的碳减排成本;${C_R}\left( {{E_R}(t)} \right) $ 表示零售商的低碳宣传成本;$ {k_M} > 0 $ 表示制造商的碳减排成本系数;$ {k_R} > 0 $ 表示零售商的低碳宣传成本系数。假设2. 为激励零售商积极宣传低碳产品,制造商为零售商分担部分低碳宣传成本,分担比例为
$ \phi (t) $ ,且$ \phi (t) < 1 $ 。假设3. 单位产品的碳减排量是动态变化的过程,且与制造商的碳减排努力程度正相关,又会因减排设备老化问题出现自然衰减现象。借鉴徐春秋等[14]55-56的微分方程来刻画变化过程
$$ \left\{ \begin{gathered} x'\left( t \right) = \gamma \;{E_M}\left( t \right) - \delta \;x\left( t \right) \\ 0 \leqslant x(t) \leqslant {d_0} \\ \end{gathered} \right. $$ (3) 式中:
$ x(t) \geqslant 0 $ 表示制造商在$ t $ 时刻所生产的单位产品的碳减排量,并且初始碳减排量为$ x(0) = {x_0} \geqslant 0 $ ;$ \gamma > 0 $ 表示制造商进行碳减排努力对单位产品碳减排量的影响系数;$ \delta > 0 $ 表示碳减排量的自然衰减系数;$ {d_0} > 0 $ 表示制造商未进行碳减排努力时的单位产品碳排放量。假设4. 市场需求受到低碳产品的碳减排量和零售商的低碳宣传努力程度的影响,需求函数可表示为
$$ Q(t) = \alpha + \beta \;{E_R}(t) + \theta \;x(t)\;\;\; $$ (4) 式中:
$Q(t) $ 表示低碳产品的需求量;$ \alpha > 0 $ 表示不进行碳减排和低碳宣传时的市场潜在需求量;$ \beta > 0 $ 和$ \theta > 0 $ 分别表示低碳宣传努力程度和单位产品碳减排量对市场需求的影响系数,满足$ \theta {d_0} < \alpha $ 。假设5. 生产过程中造成的碳排放需要按照规定缴纳碳税,则生产
$ Q $ 个单位的产品的碳税成本函数可表示为$$ {C_1}\left( {x(t)} \right) = \eta \left( {{d_0} - x(t)} \right)Q(t) $$ (5) 制造商和零售商的边际利润分别为
$ {\pi _M} > 0 $ 和$ {\pi _R} > 0 $ 。式(5)中$ \eta $ 表示制造商为每单位碳排放量所需缴纳的税额,满足$ 0 \leqslant \eta < {\pi _M}/{d_0} $ 。当$ \eta = 0 $ 时,政府不实施碳税政策。假设6. 制造商和零售商的目标均是在无限时间区间内最大化自身的利润,且在这个过程中
$ \rho > 0 $ ,$\rho $ 表示折现因子。假设7. 借鉴王一雷等[20]对
$ {k_M} $ 和$ {k_R} $ 的处理,假设它们远大于模型中其他参数,于是就有$${\left( {2\delta + \rho } \right)^2} - \dfrac{{8{\gamma ^2}}}{{{k_M}}}\left( {\dfrac{{{\eta ^2}{\beta ^2}}}{{2{k_R}}} + \theta \eta } \right)>0 $$ (6) $$ {\left( {2\delta + \rho } \right)^2} - \dfrac{{8{\gamma ^2}\theta \eta }}{{{k_M}}} > 0 $$ (7) 为下文表述简便,记
$$ {\Delta _1} = \sqrt {{{\left( {2\delta + \rho } \right)}^2} - \dfrac{{8{\gamma ^2}\theta \eta }}{{{k_M}}}}$$ (8) $$ {\Delta _2} = \sqrt {{{\left( {2\delta + \rho } \right)}^2} - \dfrac{{8{\gamma ^2}}}{{{k_M}}}\left( {\dfrac{{{\eta ^2}{\beta ^2}}}{{2{k_R}}} + \theta \eta } \right)} $$ (9) 三、 模型的建立与求解
在碳税政策下,为分析成本分担契约能否实现制造商和零售商最优利润的Pareto改善,基于问题描述和假设,建立两种微分博弈模型:首先,研究无成本分担契约下碳税政策对制造商和零售商长期最优策略和利润的影响;其次,在碳税政策和成本分担契约下,探索供应链成员的长期最优决策及其利润。
(一) 无成本分担模型(
$ N $ )研究无成本分担契约的最优决策可以为成本分担契约的设计提供供应链成员的参与约束条件,并为分析契约的协调效果提供比较对象。在无成本分担契约下,制造商首先决定其碳减排努力程度,然后零售商再决定自身的低碳宣传努力程度。
由假设6可知,制造商和零售商的目标均是在无限时间区间内最大化自身的利润,且具有相同的折现因子
$ \rho $ ,于是可得二者的决策问题分别为$$ J_M^N = \mathop {\max }\limits_{{E_M}} \int_0^\infty {{e^{ - \rho t}}} \left\{ \begin{gathered} {\pi _M}Q(t) - \frac{1}{2}{k_M}E_M^2(t) - \\ \eta \left( {{d_0} - x(t)} \right)Q(t) \\ \end{gathered} \right\}dt $$ (10) $$ J_R^N = \mathop {\max }\limits_{{E_R}} \int_0^\infty {{e^{ - \rho t}}} \left\{ {{\pi _R}Q(t) - \frac{1}{2}{k_R}E_R^2(t)} \right\}dt\; $$ (11) 为确定供应链各成员的反馈均衡策略,运用动态规划中的Hamilton-Jacobi-Bellman方程(以下简称“HJB方程”)进行求解。参照已有研究的常规做法,假设模型中的各个参数均是与时间无关的常数。同时,为简化起见,下文不再列出时间。
命题1. 在无成本分担模型中,博弈双方的均衡结果如下:
A. 制造商单位产品碳减排量的最优轨迹为
$$ {x^{N * }}(t) = \left( {{x_0} + x_\infty ^N} \right){e^{{A^N}t}} - x_\infty ^N $$ (12) 其中
$$ {x}_{\infty }^{N}=\dfrac{4{\gamma }^{2}\left({\pi }_{M}\theta -\eta {d}_{0}\theta +\eta \alpha +\eta {\pi }_{R}{\beta }^{2}/{k}_{R}\right)}{{k}_{M}({\rho }^{2}-{\Delta }_{1}^{2})}$$ (13) $$ {A^N} = \dfrac{{\rho - {\Delta _1}}}{2}$$ (14) B. 制造商和零售商的微分博弈均衡策略为
$$ E_M^{N * } = \frac{{2\delta + \rho }}{{2\gamma }}x + \frac{{2{\gamma ^2}\left( {{\pi _M}\theta - \eta {d_0}\theta + \eta \alpha + \eta \dfrac{{{\pi _R}{\beta ^2}}}{{{k_R}}}} \right)}}{{{k_M}(\rho + {\Delta _1})}} $$ (15) $$ E_R^{N * } = \frac{{{\pi _R}\beta }}{{{k_R}}} $$ (16) C. 制造商和零售商的最优利润值函数分别为
$$ J_M^{N * }\left( {x,t} \right) = {e^{ - \rho t}}\left( {a_2^{N * }{x^2} + a_1^{N * }x + a_0^{N * }} \right) $$ (17) $$ J_R^{N * }\left( {x,t} \right) = {e^{ - \rho t}}\left( {b_1^{N{\text{*}}}x + b_0^{N{\text{*}}}} \right) $$ (18) 其中
$$ a_2^{N * } = \frac{{2\delta + \rho - {\Delta _1}}}{{{{4{\gamma ^2}} \mathord{\left/ {\vphantom {{4{\gamma ^2}} {{k_M}}}} \right. } {{k_M}}}}} $$ (19) $$ a_1^{N * } = \frac{{2\left( {{\pi _M}\theta - \eta {d_0}\theta + \eta \alpha + \eta {{{\pi _R}{\beta ^2}} \mathord{\left/ {\vphantom {{{\pi _R}{\beta ^2}} {{k_R}}}} \right. } {{k_R}}}} \right)}}{{\rho + {\Delta _1}}} $$ (20) $$ \begin{split} a_0^{N * } = & \frac{{{\pi _M}\alpha - \eta {d_0}\alpha }}{\rho } + \frac{{{\pi _M}{\pi _R}{\beta ^2} - \eta {d_0}{\pi _R}{\beta ^2}}}{{\rho {k_R}}} + \\ & \frac{{2{\gamma ^2}\left( {{\pi _M}\theta - \eta {d_0}\theta + \eta \alpha + \eta {{{\pi _R}{\beta ^2}} / {{k_R}}}} \right)}}{{\rho {k_M}{{\left( {\rho + {\Delta _1}} \right)}^2}}} \\ \end{split} $$ (21) $$ b_1^{N * } = \frac{{2{\pi _R}\theta }}{{\rho + {\Delta _1}}} $$ (22) $$ \begin{split} b_0^{N * } =& \frac{{{\pi _R}\alpha }}{\rho } + \frac{{\pi _R^2{\beta ^2}}}{{2{k_R}\rho }} + \frac{{4{\pi _R}\theta {\gamma ^2}\left( {{\pi _M}\theta - \eta {d_0}\theta } \right)}}{{\rho {k_M}{{\left( {\rho + {\Delta _1}} \right)}^2}}} + \\ &\frac{{4{\pi _R}\theta {\gamma ^2}\left( {\eta \alpha + \eta {{{\pi _R}{\beta ^2}} / {{k_R}}}} \right)}}{{\rho {k_M}{{\left( {\rho + {\Delta _1}} \right)}^2}}} \\ \end{split} $$ (23) 证明:应用逆向归纳法,首先求解零售商的最优决策。根据式(11),记零售商在
$ t $ 时刻的最优利润值函数为$$ J_R^{N * }(x,t) = {e^{ - \rho t}}V_R^N(x) $$ (24) 其中
$$ V_R^N(x) = \mathop {\max }\limits_{{E_R}} \displaystyle\int_t^\infty {{e^{ - \rho \left( {s - t} \right)}}\left\{ {{\pi _R}Q - {C_R}\left( {{E_R}} \right)} \right\}} ds $$ (25) 进而,有
$ V_R^N\left( x \right) $ 满足如下HJB方程$$ \rho V_R^N(x) = \mathop {\max }\limits_{{E_R}} \left\{ \begin{gathered} {\pi _R}\left( {\alpha + \beta {E_R} + \theta x} \right) - \frac{1}{2}{k_R}E_R^2 + \\ V_R^{N'}(x)\left( {\gamma {E_M} - \delta x} \right) \\ \end{gathered} \right\} $$ (26) 易知,式(26)是关于
$ {E_R} $ 的凹函数。因此,对式(26)右端关于$ {E_R} $ 求一阶偏导,可得式(26)的最大化条件$$ {E_R} = \frac{{{\pi _R}\beta }}{{{k_R}}} $$ (27) 式(27)是零售商的反应函数,据此可知,零售商的低碳宣传努力程度
$ {E_R} $ 关于自身边际收益$ {\pi _R} $ 和对需求的影响系数$ \beta $ 递增,关于低碳宣传努力成本系数$ {k_R} $ 递减。根据式(10),记制造商在
$ t $ 时刻的最优利润值函数为$$ J_M^{N * }(x,t) = {e^{ - \rho t}}V_M^N\left( x \right) $$ (28) 其中
$$ V_M^N(x) = \mathop {\max }\limits_{{E_M}} \displaystyle\int_t^\infty {{e^{ - \rho \left( {s - t} \right)}}\left\{ \begin{gathered} {\pi _M}Q - {C_M}\left( {{E_M}} \right) - \\ \eta \left( {{d_0} - x} \right)Q \\ \end{gathered} \right\}} ds $$ (29) 进而,有
$ V_M^N\left( x \right) $ 满足如下HJB方程$$ \rho V_M^N(x) = \mathop {\max }\limits_{{E_M}} \left\{ \begin{gathered} {\pi _M}\left( {\alpha + \beta {E_R} + \theta x} \right) - \frac{1}{2}{k_M}E_M^2 - \\ \eta \left( {{d_0} - x} \right)\left( {\alpha + \beta {E_R} + \theta x} \right) + \\ V_M^{N'}(x)\left( {\gamma {E_M} - \delta x} \right) \\ \end{gathered} \right\} $$ (30) 将式(27)代入式(30)可得
$$ \rho V_M^N(x) = \mathop {\max }\limits_{{E_M}} \left\{ \begin{gathered} {\pi _M}\left( {\alpha + \beta \frac{{{\pi _R}\beta }}{{{k_R}}} + \theta x} \right) - \frac{1}{2}{k_M} \\ E_M^2 - \eta \left( {{d_0} - x} \right)(\alpha + \beta \frac{{{\pi _R}\beta }}{{{k_R}}} + \\ \theta x) + V_M^{N'}(x)\left( {\gamma {E_M} - \delta x} \right) \\ \end{gathered} \right\} $$ (31) 已知式(31)是关于
$ {E_M} $ 的凹函数,根据最大化的一阶条件可得$$ {E_M} = \frac{{V_M^{N'}(x)\gamma }}{{{k_M}}} $$ (32) 式(32)是制造商的反应函数,据此可知,制造商的碳减排努力程度关于自身碳减排努力对产品碳减排量的影响系数
$ \gamma $ 递增,即碳减排努力程度对减排量的提升影响越大,制造商越努力减排;关于自身碳减排成本系数$ {k_M} $ 递减,即制造商的碳减排成本越高,制造商的碳减排努力程度越低。将式(27)和式(32)代入式(26)和式(31),可得
$$ \rho V_R^N(x) = \left\{ \begin{gathered} \left( {{\pi _R}\theta - \delta V_R^{N'}(x)} \right)x + {\pi _R}\alpha + \\ \frac{{{\pi _R}^2{\beta ^2}}}{{2{k_R}}} + \frac{{\gamma V_R^{N'}(x)V_M^{N'}(x)}}{{{k_M}}} \\ \end{gathered} \right\} $$ (33) $$ \begin{split} & \rho V_M^N(x) = \theta \eta {x^2} + \left( \begin{gathered} {\pi _M}\theta - \delta V_M^{N'}(x) - \eta {d_0}\theta + \\ \eta \alpha + \frac{{\eta {\beta ^2}{\pi _R}}}{{{k_R}}} \\ \end{gathered} \right)x + \\ &{\pi _M}\alpha + \frac{{{\pi _M}{\beta ^2}{\pi _R}}}{{{k_R}}} + \frac{{{\gamma ^2}V_M^{N'}(x)}}{{2{k_M}}} - \eta {d_0}\alpha - \frac{{\eta {d_0}{\pi _R}{\beta ^2}}}{{{k_R}}}\; \\ \end{split} $$ (34) 观察式(33)和式(34)微分方程的特点,猜测关于
$ x $ 的二次函数和线性函数分别是制造商和零售商HJB方程的解。于是,设值函数$ V_M^{N * }\left( x \right) $ 和$ V_R^{N * }\left( x \right) $ 为$$\left\{\begin{array}{*{20}{l}} V_M^{N * }(x) = a_2^N{x^2} + a_1^Nx + a_0^N \\ V_R^{N * }(x) = b_1^Nx + b_0^N \end{array}\right.$$ (35) 其中,
$ a_2^N $ 、$ a_1^N $ 、$ a_0^N $ 、$ b_1^N $ 和$ b_0^N $ 为待定常数。将式(35)代入式(34),可得$$ \begin{split} &\rho \left( {a_2^N{x^2} + a_1^Nx + a_0^Nx} \right) = \\ &\theta \eta {x^2} + \left( {{\pi _M}\theta - \delta V_M^{N'}(x) - \eta {d_0}\theta + \eta \alpha + \frac{{\eta {\beta ^2}{\pi _R}}}{{{k_R}}}} \right)x + \\ &{\pi _M}\alpha + \frac{{{\pi _M}{\beta ^2}{\pi _R}}}{{{k_R}}} + \frac{{{\gamma ^2}V_M^{N'}(x)}}{{2{k_M}}} - \eta {d_0}\alpha - \frac{{\eta {d_0}{\pi _R}{\beta ^2}}}{{{k_R}}}\; \\ \end{split} $$ (36) 整理式(36),令等式两端同类项的系数相等,有
$$ \left\{ \begin{gathered} \rho a_2^N = \theta \eta - 2\delta a_2^N + {{2{\gamma ^2}{{(a_2^N)}^2}} / {{k_m}}} \\ \rho a_1^N = {\pi _M}\theta - \delta a_1^N - \eta {d_0}\theta + \eta \alpha + \frac{{\eta {\pi _R}{\beta ^2}}}{{{k_R}}} + \\ \frac{{2a_1^Na_2^N{\gamma ^2}}}{{{k_M}}} \\ \rho a_0^N = {\pi _M}\alpha + \frac{{{\pi _R}{\pi _M}{\beta ^2}}}{{{k_R}}} + \frac{{{\gamma ^2}{{\left( {a_1^N} \right)}^2}}}{{2{k_M}}} - \eta {d_0}\alpha - \\ \eta {d_0}\frac{{{\pi _R}{\beta ^2}}}{{{k_R}}} \\ \end{gathered} \right. $$ (37) 求解该方程组,可得
$ a_2^{N{\text{*}}} $ 、$ a_1^{N{\text{*}}} $ 和$ a_0^{N{\text{*}}} $ 的值如式(19)—式(21)所示。需要指出的是,在求解$ a_2^N $ 时会出现两个解,其中较大的解当$ t \to + \infty $ 时会导致单位产品碳减排量发散,因此取较小的解。同样的方法,可求得$ b_1^{N * } $ 和$ b_0^{N * } $ 分别为式(22)和式(23)。再将这些待定常数代入式(35)就可以得到$ V_M^{N * }\left( x \right) $ 和$ V_R^{N * }\left( x \right) $ 的表达式为$$ V_M^{N * }\left( x \right) = a_2^{N * }{x^2} + a_1^{N * }x + a_0^{N * } $$ (38) $$ V_R^{N * }\left( x \right) = b_1^{N * }x + b_0^{N * } $$ (39) 一方面,将式(38)的一阶导数代入式(32)可得博弈双方的反馈均衡策略
$ E_M^{N * } $ 和$ E_R^{N * } $ 。再将$ E_M^{N * } $ 代入状态方程并求解,可知制造商单位产品碳减排量的最优轨迹如式(12)所示。另一方面,将式(32)和(39)分别代入式(24)和式(26),得到制造商和零售商各自最优利润值函数分别如式(17)和式(18)所示。命题1给出无成本分担契约下,在制造商和零售商组成的供应链动态减排系统中,单位产品的最优碳减排量、供应链成员的最优碳减排努力程度和低碳宣传努力程度是如何随时间的推移而变化的。该命题表明,为实现最优利润,供应链成员需要按照时间的推移不断调整其最优决策,进而单位产品的最优碳减排量也随之不断变化。
推论1. 单位产品碳减排量的稳定值
$ x_\infty ^N $ 、制造商的碳减排努力程度$ E_M^{N * } $ 和零售商的最优利润值函数$ J_R^{N * }\left( {x,t} \right) $ 均与碳税税额$ \eta $ 正相关;制造商的最优利润值函数$ J_M^{N * }\left( {x,t} \right) $ 与碳税税额$ \eta $ 负相关;零售商的低碳宣传努力程度$ E_R^{N * } $ 与$ \eta $ 无关。推论1表明,随着碳税税额的提高,制造商产品的碳减排量逐渐增大,进而扩大市场需求,因此零售商利润随之提高,但对于制造商而言销量增加的同时生产成本也在增加,且后者的增加幅度超过了前者带来的利润增加幅度,因而制造商利润随之降低。此外,在无成本分担契约下,零售商的低碳宣传努力程度不受碳税政策的影响,然而低碳宣传在一定程度上有利于增强消费者的环保意识,降低消费者对低碳产品价格的敏感度,进而影响供应链的系统利润。因此,在无成本分担契约下,制造商可以考虑通过收益共享等其他契约,激励零售商加强产品低碳宣传。
(二) 成本分担模型(
$ Y $ )进一步,研究成本分担契约对博弈双方的均衡策略和最优利润值函数的影响,探究成本分担契约能否使供应链成员的利润达到Pareto改善。在成本分担模型中,制造商首先决定其碳减排努力程度和为零售商分担的低碳宣传成本比例;然后,零售商再决定其低碳宣传努力程度。此时,制造商和零售商的最优决策问题分别为
$$ J_M^Y = \mathop {\max }\limits_{{E_M},\varphi } \int_0^\infty {{e^{ - \rho t}}} \left\{ \begin{gathered} {\pi _M}Q - \frac{1}{2}{k_M}E_M^2 - \frac{1}{2}\varphi {k_R}E_R^2 - \\ \eta \left( {{d_0} - x} \right)Q \\ \end{gathered} \right\}dt $$ (40) $$ J_R^Y = \mathop {\max }\limits_{{E_R}} \int_0^\infty {{e^{ - \rho t}}} \left\{ {{\pi _R}Q - \frac{1}{2}\left( {1 - \varphi } \right){k_R}E_R^2} \right\}dt $$ (41) 命题2. 在成本分担模型中,博弈双方的均衡结果如下:
A. 制造商单位产品碳减排量的最优轨迹为
$$ {x^{Y * }}\left( t \right) = \left( {{x_0} + x_\infty ^Y} \right){e^{{A^Y}t}} - x_\infty ^Y $$ (42) 其中
$$ x_\infty ^Y = \dfrac{{{\pi _M}\theta - \eta {d_0}\theta + \eta \alpha + \dfrac{{\eta {\pi _R}{\beta ^2}}}{{{k_R}}} + \dfrac{{\left( {2{\pi _M} + {\pi _R}} \right){\beta ^2}\eta }}{{2{k_R}}}}}{{{k_M}\left( {{\rho ^2} - \Delta _2^2} \right)/4{\gamma ^2}}} $$ (43) $$ {A^Y} = \dfrac{{\rho - {\Delta _2}}}{2}$$ (44) B. 制造商和零售商的微分博弈均衡策略为
$$ {\phi }^{\text{*}}=\frac{2\left[{\pi }_{M}-\eta ({d}_{0}-x)\right]-{\pi }_{R}}{2\left[{\pi }_{M}-\eta ({d}_{0}-x)\right]+{\pi }_{R}}, $$ (45) $$ E_R^{Y * } = \frac{{2\beta \left[ {{\pi _M} - \eta \left( {{d_0} - x} \right)} \right] + \beta {\pi _R}}}{{2{k_R}}} $$ (46) $$ \begin{split} E_M^{Y * } = & \frac{{2\delta + \rho - {\Delta _2}}}{{2\gamma }}x + \frac{{2\gamma \left( {{\pi _M}\theta - \eta {d_0}\theta + \eta \alpha } \right)}}{{{k_M}\left( {\rho + {\Delta _2}} \right)}} - \\ & \dfrac{{2\gamma \left( {\dfrac{{{\eta ^2}{d_0}{\beta ^2}}}{{{k_R}}} + \dfrac{{\left( {2{\pi _M} + {\pi _R}} \right){\beta ^2}\eta }}{{2{k_R}}}} \right)}}{{{k_M}\left( {\rho + {\Delta _2}} \right)}} \\ \end{split}$$ (47) C. 制造商和零售商各自的最优利润值函数分别为
$$ J_M^{Y * }\left( {x,t} \right) = {e^{ - \rho t}}\left( {a_2^{Y{\text{*}}}{x^2} + a_1^{Y{\text{*}}}x + a_0^{Y{\text{*}}}} \right) $$ (48) $$ J_R^{Y * }\left( {x,t} \right) = {e^{ - \rho t}}\left( {b_1^{Y{\text{*}}}x + b_0^{Y{\text{*}}}} \right) $$ (49) 其中
$$ a_2^{Y * } = \frac{{2\delta + \rho - {\Delta _2}}}{{{{4{\gamma ^2}} / {{k_M}}}}} $$ (50) $$ \begin{split} a_1^{Y * } = & 2\left[ {{\pi _M}\theta - \eta {d_0}\theta + \eta \alpha + \frac{{\left( {2{\pi _M} + {\pi _R}} \right){\beta ^2}\eta }}{{2{k_R}}}} \right. - \\ & {{\left. {\frac{{{\eta ^2}{d_0}{\beta ^2}}}{{{k_R}}}} \right]} \Big/ {(\rho + {\Delta _2})}} \\ \end{split} $$ (51) $$ \begin{split} a_0^{Y * } = & \frac{{{\pi _M}\alpha - \eta {d_0}\alpha }}{\rho } + \left[ {{{\left( {2{\pi _M} + {\pi _R}} \right)}^2}{\beta ^2} - } \right. \\ &{{\left. { + 4{{\left( {2{\pi _M} + {\pi _R}} \right)}^2}{\beta ^2}\eta {d_0} + 4{\eta ^2}d_0^2{\beta ^2}} \right]} \mathord{\left/ {\vphantom {{\left. { + 4{{\left( {2{\pi _M} + {\pi _R}} \right)}^2}{\beta ^2}\eta {d_0} + 4{\eta ^2}d_0^2{\beta ^2}} \right]} {(8\rho {k_R}) + 2{\gamma ^2}}}} \right. } {(8\rho {k_R}) + 2{\gamma ^2}}} \\ &{{\left[ {{\pi _M}\theta - \eta {d_0}\theta + \eta \alpha + \frac{{\eta {\beta ^2}\left( {2{\pi _M} + {\pi _R} - 2\eta {d_0}} \right)}}{{2{k_R}}}} \right]} \Big/ {}} \\ &\left[ {\rho {k_M}{{\left( {\rho + {\Delta _2}} \right)}^2}} \right] \\ \end{split} $$ (52) $$ b_1^{Y * } = \frac{{2{\pi _R}\theta + \eta {{{\pi _R}{\beta ^2}} \mathord{\left/ {\vphantom {{{\pi _R}{\beta ^2}} {{k_R}}}} \right. } {{k_R}}}}}{{\rho + {\Delta _2}}} $$ (53) $$ \begin{split} b_0^{Y * } = &\frac{{{\pi _R}\alpha }}{\rho } + \frac{{{\pi _R}{\beta ^2}\left( {2{\pi _M} - 2\eta {d_0} + {\pi _R}} \right)}}{{4{k_R}\rho }} + \left\{ {2{\gamma ^2}\Bigg( {2{\pi _R}} } \theta +\right. \\ & { \frac{{\eta {\pi _R}{\beta ^2}}}{{{k_R}}}} \Bigg)\Bigg[ {{\pi _M}\theta - \eta {d_0}\theta + \eta \alpha + \frac{{\eta \left( {2{\pi _M} + {\pi _R}} \right)}}{{{{2{k_R}} / {{\beta ^2}}}}} - } \\ &{{\left. { {\frac{{{\eta ^2}{d_0}{\beta ^2}}}{{{k_R}}}} \Bigg]} \right\}} \Big/ {\left[ {\rho {k_M}{{\left( {\rho + {\Delta _2}} \right)}^2}} \right]}} \\ \end{split} $$ (54) 证明: 采用逆向归纳法进行求解,首先求零售商的决策。根据式(41),记零售商在
$ t $ 时刻的最优利润值函数为$$ J_R^{Y * }\left( {x,t} \right) = {e^{ - \rho t}}V_R^Y\left( x \right) $$ (55) 其中
$$ V_R^Y\left( x \right) = \mathop {\max }\limits_{{E_R}} \int_0^\infty {{e^{ - \rho \left( {s - t} \right)}}} \left\{ {{\pi _R}Q - \frac{1}{2}\left( {1 - \phi } \right){k_R}E_R^2} \right\}ds $$ (56) 进而,有
$ V_R^Y\left( x \right) $ 满足如下HJB方程$$ \rho V_R^Y(x) = \mathop {\max }\limits_{{E_R}} \left\{ \begin{gathered} {\pi _R}\left( {\alpha + \beta {E_R} + \theta x} \right) - \frac{1}{2}\left( {1 - \phi } \right) \\ {k_R}E_R^2 + V_R^{Y'}(x)\left( {\gamma {E_M} - \delta x} \right) \\ \end{gathered} \right\} $$ (57) 易知式(57)是关于
$ {E_R} $ 的凹函数。对式(57)右端关于$ {E_R} $ 求一阶偏导,可得式(57)的最大化条件$$ {E_R} = \frac{{{\pi _R}\beta }}{{{k_R}\left( {1 - \phi } \right)}} $$ (58) 由式(58)可知,零售商的低碳宣传努力程度
$ {E_R} $ 随着制造商为零售商分担低碳宣传成本比例$ \phi $ 的增大而增大。根据式(40),记制造商在
$ t $ 时刻的最优利润值函数为$$ J_M^{Y * }\left( {x,t} \right) = {e^{ - \rho t}}V_M^Y\left( x \right) $$ (59) 其中
$$ V_M^Y\left( x \right) = \int_0^\infty {{e^{ - \rho \left( {s - t} \right)}}} \left\{ \begin{gathered} {\pi _M}Q - \frac{1}{2}{k_M}E_M^2 - \frac{1}{2}\phi {k_R} \\ E_R^2 - \eta \left( {{d_0} - x} \right)Q \\ \end{gathered} \right\}ds $$ (60) 进而,有
$ V_M^Y\left( x \right) $ 满足如下HJB方程$$ \rho V_M^Y\left( x \right) = \left\{ \begin{gathered} {\pi _M}\left( {\alpha + \beta {E_R} + \theta x} \right) - \frac{1}{2}{k_M}E_M^2 - \\ \frac{1}{2}\phi {k_R}E_R^2 - \eta \left( {{d_0} - x} \right)\left( {\alpha + \beta {E_R} + } \right. \\ \left. {\theta x} \right) + {{V'}_M}\left( x \right)\left( {\gamma {E_M} - \delta x} \right) \\ \end{gathered} \right\}\; $$ (61) 将式(58)代入上式,再关于
$ {E_M} $ 和$ \phi $ 求驻点得$$ {E_M} = \frac{{\gamma V_M^{Y'}\left( x \right)}}{{{k_M}}} \text{,} \phi = \frac{{2\left[ {{\pi _M} - \eta \left( {{d_0} - x} \right)} \right] - {\pi _R}}}{{2\left[ {{\pi _M} - \eta \left( {{d_0} - x} \right)} \right] + {\pi _R}}} $$ (62) 式(62)是制造商的反应函数,求导可知,制造商为零售商分担的低碳宣传成本比例与制造商的边际利润正相关,而与零售商的边际利润负相关。进一步,因为
$ {\pi _M} - \eta {d_0} > 0$ ,所以当$ 2{\pi _M} - 2\eta \left( {{d_0} - x} \right) - $ $ {\pi _R} > 0 $ 时有$ \varphi > 0 $ ,即此时制造商会为零售商分担低碳宣传成本;否则,制造商不仅不为零售商分担低碳宣传成本,还会以零售商的低碳宣传成本为基础收取一定的费用。将
$ {E_R} $ 、$ {E_M} $ 和$ \phi $ 代入式(57)和式(61),可得$$ \begin{split} & \rho V_M^Y(x) = \left( {\frac{{{\eta ^2}{\beta ^2}}}{{2{k_R}}} + \eta \theta } \right){x^2} + x\Bigg[ {{\pi _M}\theta - \delta V_M^{Y'}(x) - } \\ & {\eta {d_0}\theta + \eta \alpha - \frac{{\eta {\beta ^2}{\pi _R}}}{{{k_R}}} + \frac{{\left( {2{\pi _M} + {\pi _R}} \right){\beta ^2}\eta }}{{2{k_R}}}} \Bigg] + {\pi _M}\alpha + \\ & \frac{{{\gamma ^2}V_M^{Y'}(x)}}{{2{k_M}}} - \eta {d_0}\alpha + \frac{{{\eta ^2}d_0^2{\beta ^2}}}{{2{k_R}}} - \frac{{\left( {2{\pi _M} + {\pi _R}} \right){\beta ^2}\eta {d_0}}}{{2{k_R}}} + \\ & \frac{{\left( {2{\pi _M} + {\pi _R}} \right){\beta ^2}}}{{8{k_R}}} \\ \end{split}$$ (63) $$ \begin{split} \rho V_R^Y(x) = \left( {{\pi _R}\theta - \delta V_R^{Y'}(x)} \right)x + {\pi _R}\alpha + {\pi _R}{\beta ^2}\big[ {{\pi _M} - } \\ { {\eta \left( {{d_0} - x} \right) + {\pi _R}} \big]} / \left[{2{k_R} + \frac{{{\gamma ^2}V_R^{Y'}(x)V_M^{Y'}(x)}}{{{k_M}}}}\right] \\ \end{split}$$ (64) 观察式(63)和式(64)两个微分方程的特点,猜测关于
$ x $ 的二次函数和线性函数分别是制造商和零售商HJB方程的解。于是,设值函数$ V_M^{Y * }\left( x \right) $ 和$ V_R^{Y * }\left( x \right) $ 为$$\left\{\begin{array}{*{20}{l}} V_M^{Y*}\left( x \right) = a_2^Y{x^2} + a_1^Yx + a_0^Y \\ V_R^{Y*}(x) = b_1^Yx + b_0^Y \end{array}\right.$$ (65) 其中,
$ a_2^Y $ 、$ a_1^Y $ 、$ a_0^Y $ 、$ b_1^Y $ 和$ b_0^Y $ 均为待定常数。同命题1的证明过程,将式(65)分别代入式(63)和式(64),并令同类项的系数相等,可得关于$ a_2^Y $ 、$ a_1^Y $ 、$ a_0^Y $ 、$ b_1^Y $ 和$ b_0^Y $ 的约束方程组,再求解该方程组可知$ a_2^{Y*} $ 、$ a_1^{Y*} $ 、$ a_0^{Y*} $ 、$ b_1^{Y*} $ 和$ b_0^{Y*} $ 的值如式(49)—式(54)所示。再将这些待定常数代入式(65)可以得到$$\left\{\begin{array}{*{20}{l}} V_M^{Y * }\left( x \right) = a_2^{Y * }{x^2} + a_1^{Y * }x + a_0^{Y * }\\ V_R^{Y * }\left( x \right) = b_1^{Y * }x + b_0^{Y * } \end{array}\right.$$ (66) 将式(66)的一阶导数代入式(62),再结合式(58)可得博弈双方的反馈均衡策略为
$ E_M^{Y * } $ 、$ E_R^{Y * } $ 和$ {\varphi ^ * } $ 。再将$ E_M^{Y * } $ 代入状态方程并求解,可知制造商单位产品碳减排量的最优轨迹如式(42)所示。进一步,将式(66)分别代入式(57)和式(61),得到制造商和零售商各自最优利润值函数分别为式(48)和式(49)。与命题1不同,命题2在成本分担契约下重新推导了产品的最优碳减排量,供应链成员的碳减排努力程度、低碳宣传努力程度以及制造商为零售商分担的低碳宣传成本比例的最优决策。对比两个命题可以发现,成本分担契约对供应链上下游的最优决策和最优利润有本质性影响。
推论2. 单位产品碳减排量的稳定值
$ x_\infty ^Y $ 、制造商的碳减排努力程度$ E_M^{Y * } $ 和零售商的最优利润值函数$ J_R^{Y * }\left( {x,t} \right) $ 均与碳税税额$ \eta $ 正相关;零售商的低碳宣传努力程度$ E_R^{Y * } $ 、制造商为零售商分担的低碳宣传成本比例$ {\phi ^ * } $ 和最优利润值函数$ J_M^{Y * }\left( {x,t} \right) $ 均与碳税税额$ \eta $ 负相关。推论2表明,在成本分担契约下,碳税政策的实施也可以有效提升制造商碳减排的积极性及其产品的碳减排量。一方面,随着碳税税额的提高,产品碳减排量及其市场需求增大,零售商利润随之提高,但制造商也因此生产成本迅速增加导致其利润不升反降。另一方面,碳税税额越高,制造商为零售商分担的低碳宣传成本比例越低,导致零售商的低碳宣传积极性随之降低。这两个方面的原因会导致制造商的低碳减排或零售商的低碳宣传成本减少,使得低碳偏好消费者对低碳产品的购买意愿下降,最终影响到市场需求。为提升上下游企业的减排投入和低碳宣传力度,政府可以通过实施碳减排补贴等政策,向制造商和零售商提供一定的降碳补贴,以改善企业对环境的负外部性,从而实现经济与环境的最佳状态。
四、 比较分析
对比命题1和命题2,可得如下结论:
命题3. 当
$ 2{\pi _M} - 2\eta ({d_0} - x) - {\pi _R} > 0 $ 时,$ E_R^{Y * } > E_R^{N * } $ ;当$ 2{\pi _M} - 2\eta ({d_0} - x) - {\pi _R} < 0 $ 时,$ E_R^{Y * } < E_R^{N * } $ 。证明:由
$ E_R^{Y * } - E_R^{N * } = \dfrac{{\beta \left( {2{\pi _M} - 2\eta ({d_0} - x) - {\pi _R}} \right)}}{{2{k_R}}} $ ,显然命题3成立。由命题3可知,当
$ 2{\pi _M} - 2\eta ({d_0} - x) - {\pi _R} > 0 $ 时,相较于无成本分担契约,在成本分担契约下零售商的低碳宣传努力程度有所提升;当$ 2{\pi _M} - 2\eta ({d_0} - $ $ x) - {\pi _R} < 0 $ 时,制造商不仅不为零售商分担低碳宣传成本,还会向零售商收取一定的费用,此时与无成本分担契约相比较,零售商的低碳宣传努力程度有所降低。在碳税政策和成本分担契约下,随着碳税税额$ \eta $ 的增大,可能使制造商由为零售商分担低碳宣传成本,逐渐转向向零售商收取一定的费用,从而导致零售商的低碳宣传积极性先升后降。结果表明,碳税政策和成本分担契约的实施对供应链上下游成员的长期合作具有决定性影响。命题4. 当
$ 2{\pi _M} - 2\eta {d_0} - {\pi _R} > 0 $ 时,有$ x_\infty ^{Y * } > x_\infty ^{N * } $ ,$ E_M^{Y * } > E_M^{N * } $ ,$ V_M^{Y * } > V_M^{N * } $ 和$ V_R^{Y * } > V_R^{N * } $ 。证明:当
$ 2{\pi _M} - 2\eta {d_0} - {\pi _R} > 0 $ 时,因为$$ \begin{split} & V_M^{Y * } - V_M^{N * } \geqslant (a_0^{Y*} - a_0^{N*}) \\ & \geqslant \frac{{{{(2{\pi _M} - {\pi _R})}^2}{\beta ^2}}}{{8\rho {k_R}}} + \frac{{(2{\pi _M} - 2\eta {d_0} - {\pi _R})\eta {\beta ^2}{\gamma ^2}}}{{\rho {k_R}{k_M}{{(\rho + {\Delta _1})}^2}}} + \\ & \frac{{({\pi _R} - 2{\pi _M})\eta {d_0}{\beta ^2}}}{{2\rho {k_R}}} + \frac{{{\eta ^2}d_0^2{\beta ^2}}}{{2\rho {k_R}}} \\ & \geqslant \frac{{{{\left[ {(2{\pi _M} - {\pi _R}) - 2\eta {d_0}} \right]}^2}{\beta ^2}}}{{8\rho {k_R}}} \\ & > 0 \\ \end{split}$$ (67) 因此,
$ V_M^{Y * } > V_M^{N * } $ 。采用同样的方法,可证得命题4的其他结论。由命题4可知,当
$ 2{\pi _M} - 2\eta {d_0} - {\pi _R} > 0 $ 时,与无成本分担契约相比较,在成本分担契约下制造商产品碳减排量、碳减排努力程度以及博弈双方的利润均有提高。这表明,当$ 2{\pi _M} - 2\eta {d_0} - {\pi _R} > 0 $ 时,成本分担契约不仅可以提升低碳产品的碳减排量,还可以实现供应链成员利润的Pareto改善,所以具有自执行性。由于供应链成员利润的表达式过于复杂,当$ 2{\pi _M} - 2\eta {d_0} - {\pi _R} < 0 $ 时,无法直接比较成本分担和无成本分担两种不同契约下的供应链成员利润大小关系。然而,研究比较分析显示,当$ 2{\pi _M} - $ $2\eta {d_0} - {\pi _R} < 0 $ 时,零售商的利润可能因为成本分担契约而降低,因此契约不满足零售商的参与约束。综上,$ 2{\pi _M} - 2\eta {d_0} - {\pi _R} > 0 $ 是成本分担契约成立的必要条件。虽然,碳税税额越高越能促进制造商减排,但是,若要实现供应链利润和碳减排的双目标Pareto优化,则应将碳税税额设置在一个合理范围内以促使成本分担契约的成立。五、 算例分析
为了进一步观察碳税政策和成本分担契约对供应链上下游成员长期联合减排和低碳宣传的影响,结合数值算例进行分析。模型参数设置如下:
$ \delta = 1 $ ,$ \rho = 0.5 $ ,$ \gamma = 2 $ ,$ \theta = 3 $ ,$ {d_0} = 1 $ ,$ \beta = 5 $ ,$ {k_R} = 100 $ ,$ {k_M} = 300 $ ,$ \alpha = 10 $ ,$ {\pi _M} = 6 $ ,$ {\pi _R} = 5 $ 。碳税税额对单位产品碳减排量的影响,如图1所示。
由图1可知,碳税政策下,单位产品的碳减排量稳定值随着碳税税额单调递增,且在成本分担契约下的碳减排量更大。成本分担前后碳减排量的差值也随着碳税税额单调递增。这说明碳税税额越高,成本分担契约对碳减排量的增强效应越明显。上述结果表明,与没有碳税政策相比,该政策的引入可以有效提升低碳产品的碳减排量,且成本分担契约能够进一步增强这一效应。
成本分担前后碳税税额对利润的影响,如图2所示。
由图2可知,成本分担前后,制造商的利润均是随着碳税税额单调递减,并且零售商的利润均是随着碳税税额单调递增。进一步,对比制造商和零售商的利润在成本分担前后的垂直距离可以发现,成本分担契约对后者利润的改善效果更优,并且对二者利润的改善效果都随着碳税税额的增大而降低。究其原因,在成本分担契约下,制造商为零售商承担了部分低碳宣传成本,零售商因此将更努力地进行低碳宣传,使得低碳产品的销量增大,给制造商和零售商带来更多的利润,从而实现二者利润的Pareto改善,同时也正是因为制造商为零售商分担了部分低碳宣传成本,导致契约对零售商利润的改善效果更优。此外,碳税税额的提高会增加制造商的生产成本,使得制造商为零售商分担的低碳宣传成本比例减小,零售商低碳宣传积极性的增强趋势因此放缓,最终导致成本分担契约对制造商和零售商利润的改善效果降低。
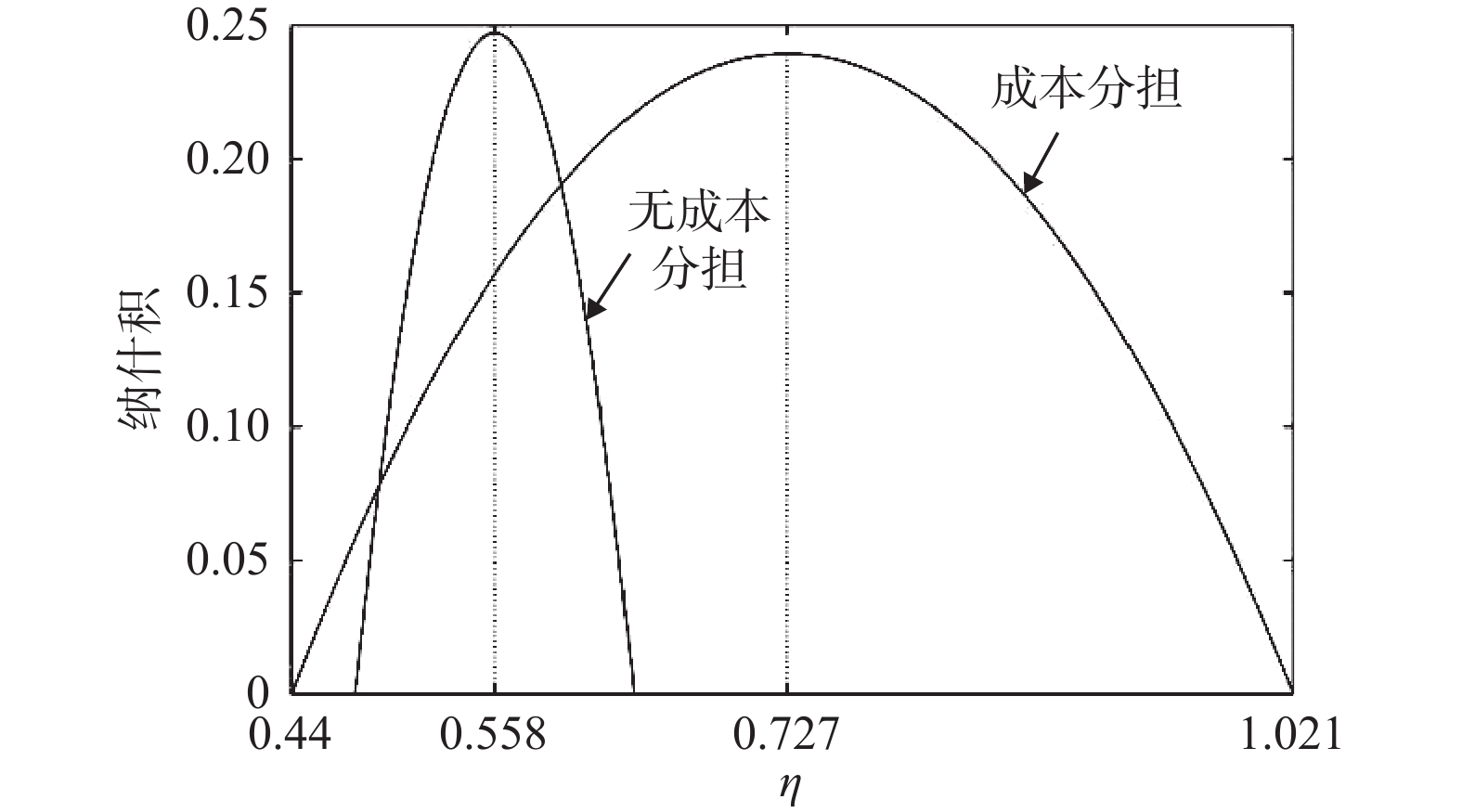
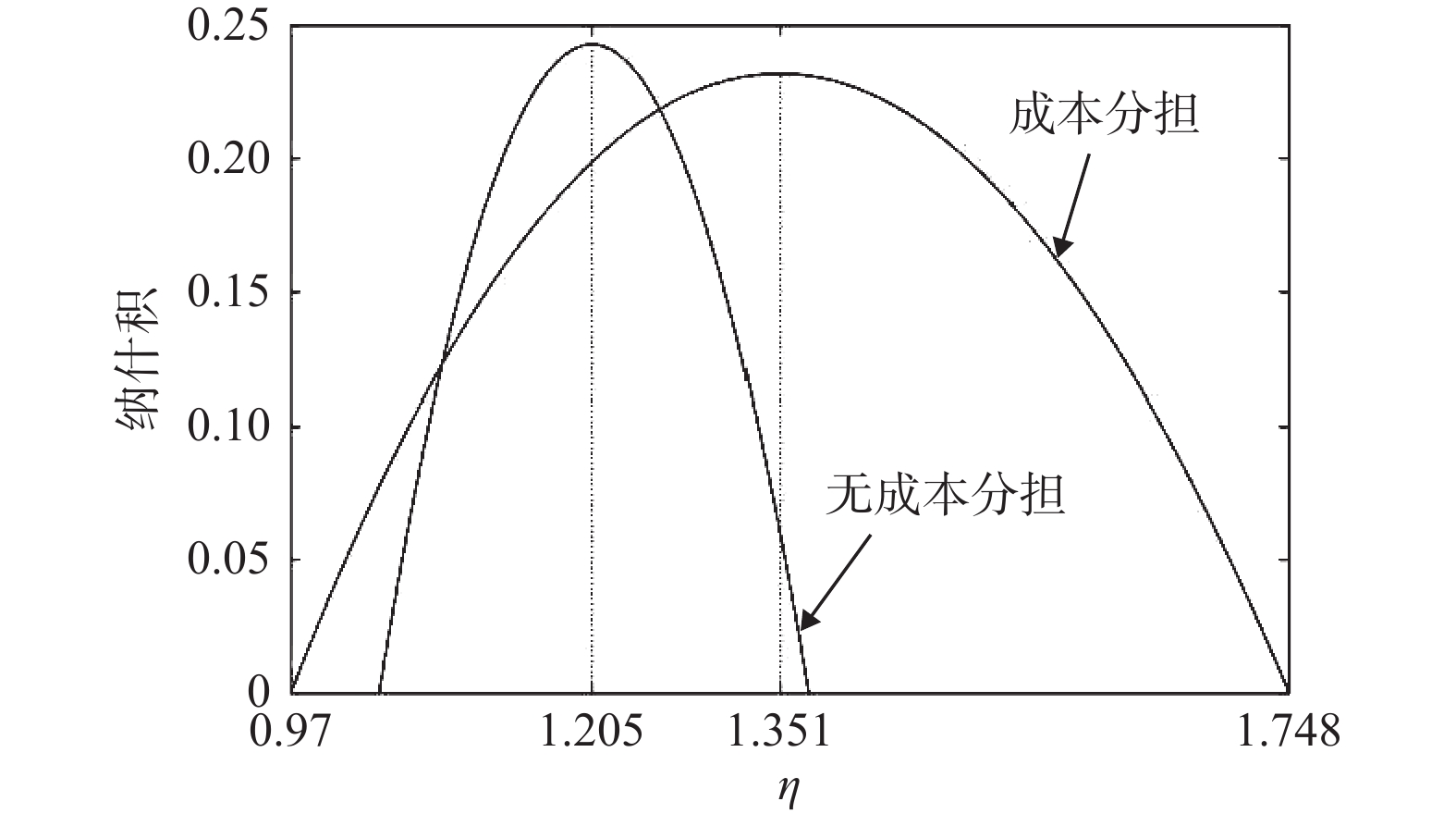
政府在制定碳税政策时,不仅应考虑低碳减排,还应考虑经济增长,也就是希望同时实现碳减排量和企业利润最大化,这是一个多目标优化问题。由于碳税税额越高致使碳减排量越大而供应链系统利润越低,因此中央政府可以按照最低的碳减排量标准设定最低碳税税额,同时按照供应链系统利润的最低要求设定最高碳税税额。在中央政府设定的碳税弹性空间中,地方政府再根据当地实际情况,给予环境和经济适宜的权重,进而核定适合当地的碳税税额。记
$ \underline x $ 和$ \underline {{V_{SC}}} $ 分别表示碳减排量和系统利润的最低标准,同时假设地方政府对环境和经济的重视程度相同。先将产品碳减排量和供应链系统利润进行标准0-1变换以消除量纲影响,再极大化二者的纳什积,即可确定碳税税额,如图3和图4所示。由图3和图4可知,与无成本分担契约相比,成本分担契约下碳税弹性空间更大及其核定的碳税税额更高;当政府对碳减排要求较低时,所需实施的碳税税额也较低。
最后,探索
$ 2{\pi _M} - 2\eta {d_0} - {\pi _R} < 0 $ 时成本分担契约对零售商利润的影响。为此,取$ \eta \in [0,\;2] $ 和$ {\pi _M} \in [3,\;6] $ ,并令其他参数保持不变。成本分担前后参数$ \eta $ 和$ {\pi _M} $ 对零售商利润的影响,如图5所示。由图5可知,一方面,当
$ 2{\pi _M} - 2\eta {d_0} - {\pi _R} > 0 $ 时,成本分担契约可以提升零售商的利润;另一方面,当$ \eta $ 和$ {\pi _M} $ 分别靠近2和3时(此时,$ 2{\pi _M} - 2\eta {d_0} - {\pi _R} < 0 $ ),成本分担契约将降低零售商的利润。这表明,成本分担契约下制造商和零售商的参与约束条件,依赖于双方的边际利润以及碳税税额的高低。六、 结论
研究在考虑碳税政策的基础上,从供应链上下游长期联合减排与低碳宣传的角度,构建了无成本分担契约和成本分担契约两种Stackelberg微分博弈模型。通过对模型的求解和分析,所得主要结论如下:首先,与没有碳税政策相比,该政策的实施可以有效提高产品碳减排量、制造商的碳减排努力程度和零售商的利润,但会降低制造商的利润。为抵销碳税政策对制造商碳减排产生的消极影响,政府亟须建立健全清洁发展、排放贸易和联合履约等碳交易机制来提升制造企业的碳减排意愿。其次,当博弈双方的边际利润以及碳税税额满足
$ 2{\pi _M} - $ $ 2\eta {d_0} - {\pi _R} > 0 $ 时,成本分担契约可以实现制造商和零售商利润的Pareto改善,且对后者的改善效果更优。最后,成本分担契约的引入不仅可以进一步提高产品的碳减排量,还可以拓宽碳税弹性空间。为实现碳排放控制与企业利润最大化的双赢目标,政府应积极促成成本分担契约在改善供应链绩效上的条件,推动供应链上下游企业的碳减排合作。研究在碳税政策下分析成本分担契约对产品碳减排量和供应链成员利润的长期决策产生的影响,所得结论对制定碳税政策以实现环境和经济双目标优化具有指导意义。考虑到碳政策的复杂性和多样性,后续研究可以同时探讨政府补贴和碳交易等政策的约束。此外,在碳税政策和收益共享等其他契约框架下,低碳供应链的长期联合减排与低碳宣传问题也都值得深入研究。
-
[1] 习近平在第七十五届联合国大会一般性辩论上发表重要讲话[N]. 人民日报, 2020−09−23(1). [2] 国务院发展研究中心课题组, 刘世锦, 张永生. 全球温室气体减排:理论框架和解决方案[J]. 经济研究, 2009, 44(3): 4-13. [3] BRUVOLL A, LARSEN B M. Greenhouse gas emissions in Norway: Do carbon taxes work? [J]. Energy Policy, 2004, 32(4): 493-505.
[4] PETRAKIS E, POYAGO-THEOTOKY J. R&D subsidies versus R&D cooperation in a duopoly with spillovers and pollution [J]. Australian Economic, 2002, 41(1): 37-52.
[5] WESSEH P K, LIN B Q. Optimal carbon taxes for China and implications for power generation, welfare, and the environment [J]. Energy Policy, 2018, 118: 1-8.
[6] 高举红, 王海燕, 孟燕莎. 基于补贴与碳税的闭环供应链定价策略[J]. 工业工程, 2014, 17(3): 61-67. [7] 姜跃, 韩水华. 碳税规制下零售商减排成本分担对企业减排决策的影响[J]. 商业研究, 2017(8): 158-166. [8] 曹细玉, 张杰芳. 碳减排补贴与碳税下的供应链碳减排决策优化与协调[J]. 运筹与管理, 2018, 27(4): 57-61. [9] LI F, DONG S C, LI X, et al. Energy consumption-economic growth relationship and carbon dioxide emission in China [J]. Energy Policy, 2011, 39(2): 568-574.
[10] LOAIZA-RAMIREZ J P, MORENO-MANTILLA C E, REIMER T. Do consumers care about companies’ efforts in greening supply chains? Analyzing the role of protected values and the halo effect in product evaluation [J]. Cleaner Logistics and Supply Chain, 2022(3): 1-10.
[11] 朱庆华, 夏西强, 王一雷. 政府补贴下低碳与普通产品制造商竞争研究[J]. 系统工程学报, 2014, 29(5): 640-651. [12] 孙嘉楠, 肖忠东. 考虑消费者双重偏好的低碳供应链减排策略研究[J]. 中国管理科学, 2018, 26(4): 49-56. [13] 孙立成, 应梦煌, 张济建. 碳转移与消费者低碳偏好双重影响下供应链异质性产品定价与协调研究[J]. 运筹与管理, 2022, 31(2): 155-161. [14] 徐春秋, 赵道致, 原白云, 等. 上下游联合减排与低碳宣传的微分博弈模型[J]. 管理科学学报, 2016, 19(2): 53-65. [15] 赵道致, 徐春秋, 王芹鹏. 考虑零售商竞争的联合减排与低碳宣传微分对策[J]. 控制与决策, 2014, 29(10): 1809-1815. [16] 刘名武, 万谧宇, 付红. 碳交易和低碳偏好下供应链低碳技术选择研究[J]. 中国管理科学, 2018, 26(1): 152-162. [17] ZHOU Y J, YE X. Differential game model of joint emission reduction strategies and contract design in a dual-channel supply chain [J]. Journal of Cleaner Production, 2018, 190: 592-607.
[18] ZU Y F, CHEN L H, FAN Y. Research on low-carbon strategies in supply chain with environmental regulations based on differential game [J]. Journal of Cleaner Production, 2018, 177: 527-546.
[19] 王君, 程先学, 蒋雨珊, 等. 碳税政策下考虑参考碳排放的供应链成员行为选择研究[J]. 中国管理科学, 2021, 29(7): 128-138. [20] 王一雷, 夏西强, 张言. 碳交易政策下供应链碳减排与低碳宣传的微分对策研究[J]. 中国管理科学, 2022, 30(4): 155-166.




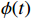














































































































































































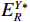











































 下载:
下载: