编者按:党的十八大以来,习近平总书记就新型工业化一系列重大理论和实践问题作出重要论述,为推进新型工业化提供了根本遵循和行动指南。新时代新征程,新型工业化作为推动经济高质量发展的重要路径,正在不断深化和拓展。为了更好地把握其基本规律,多角度展示其理论与实践成果,本刊特别策划了“新型工业化研究”系列专题,旨在从哲学、法学、经济学、管理学、艺术学等学科以及交叉学科视角,对新型工业化进行理论阐释与学术研究。本专题刊发的两篇文章,聚焦中国高新技术企业全要素生产率、国有企业特色治理与绿色绩效等前沿议题展开探讨,以期能为新型工业化相关研究提供有益借鉴。
Estimation and Analysis of Total Factor Productivity of High-Tech Enterprises in China——Based on Nonparametric Model
-
摘要:
高新技术企业是新时期高水平推进新型工业化的重要主体,也是新质生产力的主要推动者,其创新水平如何,是各界关心的重要问题。研究使用2013—2019年国家高新区企业的微观数据,构建非参数生产函数模型,放松了投入要素对产出具有线性影响的假设,并考虑高新技术企业进行投入要素投入决策时可能存在的内生性问题,利用两阶段非参数法估计高新技术企业的生产函数,计算得到企业层面的全要素生产率,从全要素生产率角度分析其创新水平。结果表明,初创高新技术企业的全要素生产率较低,总产出的提升仍处在前期要素积累阶段,主要依赖各投入要素的投入,总产出对资本要素投入较为敏感,且不同技术领域企业间的全要素生产率存在异质性。研究发现,制造型出口企业全要素生产率显著高于非出口企业,服务型出口企业全要素生产率与非出口企业无显著差异。研究为政府提供了促进中国高新技术企业发展的政策建议。
Abstract:High-tech enterprises are the important subject to promote new industrialization at a high level in the new era, and the main driver of new quality productive forces. Their innovation level is an important issue of concern to people in all walks of life. Based on the micro-data of enterprises in the national high-tech zones from 2013 to 2019, the paper constructs a non-parametric production function model, relaxes the assumption that input factors have a linear impact on output, and considers the endogenous problems that may exist when high-tech enterprises make decisions on the input factors. In addition, it uses the two-stage nonparametric method to estimate the production function of high-tech enterprises and calculates the total factor productivity at the enterprise level, thus analyzing their innovation level from the perspective of total factor productivity. The results show that the total factor productivity of start-up high-tech enterprises is relatively low. This means that the improvement of total output is still in the early stage of factor accumulation and mainly dependent on the input of various input factors. What’s more, the total output is more sensitive to the input of capital factors, and there is heterogeneity in the total factor productivity among enterprises in different technical fields. The study finds that the total factor productivity of manufacturing export enterprises is significantly higher than that of non-export enterprises, and there is no significant difference between the total factor productivity of service export enterprises and non-export enterprises. This study provides policy recommendations for the government to promote the development of high-tech enterprises in China.
-
一、 问题的提出
高新技术企业为最新科研成果的创造和落地提供发展平台,是提升国家和各产业综合实力的重要驱动,是国家重要创新策源地,是促进科技创新与产业创新对接的重要主体,能够不断推动生产力的提升,是新质生产力的主要推动者。根据高新技术领域的分类标准,高新技术企业的覆盖面甚广,涵盖8个高新技术领域和200余个小领域,包含了生活中的方方面面。2023年,中国共有178家国家高新区
① ,全国高新技术企业数量达46.3万家② 。以湖北省为例,2.5万家的高新技术企业贡献了全省企业利润的约35%,专利授权量的55%,高新技术产业增加值的70%③ 。因此,高新技术企业是带动产业转型发展的重要载体,是中国经济高质量发展的主引擎。国家高新区聚集了近80%的全国重点实验室、70%的国家制造业创新中心、78%的国家技术创新中心① ,这为高新技术企业发展提供了政策支持和优惠措施。这从另外一个侧面反映了,高新技术企业依托国家级的创新载体,有力推动着新质生产力的发展。2023 年9 月,习近平就推进新型工业化作出重要指示:“新时代新征程,以中国式现代化全面推进强国建设、民族复兴伟业,实现新型工业化是关键任务。”[1]新型工业化的根本动力是自主创新,要不断提高产业的创新能力。随着中国产业结构向传统产业的中高端环节、高技术产业、战略性新兴产业为主的方向转变,工业化要从低水平的规模型扩张转向高水平的质量效益型发展,实现这一转变必须依靠创新驱动。因此,高新技术企业作为科技创新的主体,也是推进新型工业化的重要主体。
新质生产力是高新技术企业发展的基础,其为高新技术企业的发展提供了强大的技术支撑、卓越的创新能力和广阔的市场机遇。高新技术企业通过应用新质生产力来提高技术创新水平,其技术创新水平可以通过全要素生产率的测度来反映。基于此,研究尝试对中国高新技术企业的生产函数以及全要素生产率进行估计,以研究技术创新和高端技术开发能力对企业总产出的影响,更深层次把握中国高新技术产业的发展特点与未来发展趋势,从而为推进高新区的发展和新型工业化的建设提供参考。
研究主要拟解决高新技术企业的生产函数和全要素生产率估计中的两个问题:
第一,内生性问题。企业管理者和研究人员之间的信息不对称是内生性问题的主要来源。对企业而言,在进行未来生产决策时会依赖公司自身的生存和发展情况。这意味着,在生产函数模型中,投入要素的投入量与企业层面的全要素生产率之间存在相关关系,下一期企业的全要素生产率在某种程度上可以被预测,即下一期的生产决策(如劳动、资本和中间投入)会受到该期的全要素生产率影响。然而,全要素生产率是不可被直接观测的。因此,在采用劳动、资本、原材料等投入估计全要素生产率时,会产生内生性问题,从而导致在利用生产函数模型估计全要素生产率时,面临参数识别问题。此外,样本选择偏差也可能导致内生性问题。理论上,在进行生产函数估计时应该包括所有样本,但在实际搜集数据时,只能观测到当前存活的企业数据,那些已经消失的企业数据无从得知,这就导致在对生产函数进行估计时,天然存在样本选择偏差问题。此外,内生性会导致利用最小二乘回归(OLS)估计的投入要素弹性系数结果有偏,从而产生估计参数传递偏差等问题,导致模型估计结果与实际生产不符。
第二,变量衡量问题。在确定了生产函数的形式与估计方法后,虽然从理论来讲,确定了如资本、劳动、中间投入等投入和企业总产出的概念,然而在实际应用中却没有明确指出具体的衡量指标,即学界对总产出的变量选择并没有一个具体的定论。当研究对象是工业企业时,学者往往采用“工业总产值”来衡量总产出,当研究对象是生产性服务业的企业时,学者往往采用“营业收入”或“主营业务收入”等指标来描述总产出;而对于主要产出创新成果的企业,学者往往采用“专利授权数”“专利申请数”“新产品销售收入”等变量作为总产出进行分析。
针对上述问题,研究将利用Gandhi等提出的两阶段非参数估计方法(以下简称“GNR方法”)[2]2973-3016,对中国高新技术企业的生产函数进行估计。研究旨在解决其内生性问题,探究不同产出指标对生产函数估计的影响,分析企业层面全要素生产率的分布特征,揭示中国高新技术企业和产业发展规律,以期为政府制定高新技术企业发展政策提供实证依据。
二、 文献回顾
对企业的生产函数进行估计,始终是一个重要话题,这源于其是估计投入要素产出弹性、企业全要素生产率等问题的前提。随着计量经济学的快速发展和微观数据的不断出现,如何更好地使用微观数据,有效估计企业的生产函数成为了焦点问题。由于生产决策和全要素生产率之间具有一定的相关关系,因此,采用传统的估计方法可能会产生内生性问题。处理内生性问题的模型一般分为四大类,包括工具变量法、固定效应模型、动态面板模型以及最新发展的结构模型。研究主要运用结构模型中较新提出的GNR方法开展相关讨论[2]2973-3016。
生产函数模型形式设定存在一定的内生性,其根源在于研究者无法观察到影响生产决策的一些变量投入,但这些投入对企业本身是可预知的。在此情况下,当企业在追求利润最大化时,其作出的投入决策即这些决定因素的函数,从而导致内生性问题的产生。而结构模型主要是利用企业投入要素决策和全要素生产率之间的关系,构建投资、中间投入等变量与全要素生产率之间的转换方程,从而有效地解决该问题,这类方法近年来被广泛运用于实证研究中。Olley和Pakes从企业动态演化的角度研究生产函数,基于美国通信设备业的微观企业数据,采用半参数生产函数模型,将投资数据作为全要素生产率的代理变量,较好地解决了由于投入产出相互决定带来的内生性和样本选择偏差引起的问题[3];Levinsohn和Petrin选择利用企业中间投入与全要素生产率的关系,构建转换方程,解决了企业投资调整中灵活性较差的问题,避免了剔除投资为零的数据对生产函数估计过程造成的效率损失[4];Ackerberg等提出一种新的估计方法,即第一阶段使用总产出对中间投入、劳动和资本进行非参数回归,得到对总产出的估计;第二阶段对一阶马尔科夫过程(Markov process)中的变量作非参数回归,利用矩条件进行GMM估计得到投入要素的弹性系数,有效地改善了当数据存在样本选择偏差时,前两种方法在估计中产生的多重共线性问题[5]。然而,以上三种方法均无法直接获得估计参数的标准差,故Wooldridge提出将第一、二阶段同时进行估计,使用广义矩估计方法直接得到估计参数的标准差[6]。Gandhi等提出半参数形式和柔性产出的估计方法,解决了投资作为中间投入的柔性特征,修正了用增加值作为产出衡量标准的内生性问题[7];此后,Gandhi等在此基础上继续完善和优化,将企业总产出作为产出的衡量指标,提出了GNR方法,减少了模型设定对参数估计过程中的约束,避免了估计中产生的弹性系数有偏的问题,同时采用企业的中间投入要素来刻画全要素生产率,有效解决了内生性问题[2]2973-3016。
在确定企业生产函数的模型形式后,许多学者对总产出变量的选择与衡量方法进行了讨论。对于传统制造业,研究普遍选取企业的“工业总产值”作为总产出衡量标准,吴延兵和米增渝采用Cobb-Douglas生产函数模型,利用中国制造业企业数据,将工业总产值作为企业总产出指标考察创新对技术效率的影响[8]。黄先海等采用工业企业数据库,采用产品产值作为总产出进行估计[9]。然而,根据投入产出表编制方法,非制造业企业缺少可观测的产品产值数据,在衡量如信息服务、专业技术服务等服务部门的总产出时,通常通过部门企业的营业收入、主营业务收入等财务指标进行计算[10]。同时,高新技术企业具有较强的研究开发能力和一定的核心技术知识产权,在核算营业收入时,技术收入占比较大,特别对处于初创期的高新技术企业而言,技术收入是较为重要的收入来源,故在衡量高新技术企业的总产出时,可以考虑利用技术收入指标进行衡量。此外,苗金芳等在研究中使用新产品销售收入指标来衡量企业的总产出,以此描绘生产过程中创新的产出价值[11]。
在估计出生产函数模型后,学者通常继续对全要素生产率进行更深入的分析和研究。全要素生产率,被认为是生产过程中不能由资源投入所解释的“剩余”,即生产函数模型的残余项,代表了非生产性投入要素对总产出的影响。全要素生产率表示企业资源投入转化为企业产出的生产效率,该变量不仅与技术进步有关,还反映了研究对象生产的知识水平、管理能力、制度环境和测量误差等因素[12]。谢千里等利用参数模型的设定形式,基于1998—2005年中国工企数据库计算了制造业企业的全要素生产率水平[13]。张杰等采用参数形式的生产函数模型,基于江苏当地制造业企业的微观数据对全要素生产率进行了测度,研究企业出口和其全要素生产率之间的影响机制[14]。
综上所述,现有研究大多采用参数法或半参数法对制造业企业进行生产函数估计,在估计的过程中会产生内生性、样本选择偏差等问题,对企业类型选择的约束较强。因此,研究充分考虑内生性、变量衡量等问题的影响,利用GNR方法对中国高新技术企业的生产函数和全要素生产率进行估计。根据估计结果,探究中国高新技术企业生产过程的特点,并比较不同领域全要素生产率的异同点。
三、 基于非参的生产函数估计框架
(一) 生产函数模型形式设定
对于生产函数的估计通常从设定生产函数模型形式入手,利用生产函数描述企业的生产过程。在现有研究中,生产函数的模型设定主要分为参数形式、半参数形式和非参数形式,经典的Cobb-Douglas生产函数和超越对数生产函数均属于参数模型。在结构模型中,OP估计法和LP估计法等构建的生产函数均属于半参数模型。然而,无论是参数模型还是半参数模型,其在估计的过程中往往会产生传递偏差,最后的估计结果受到模型设定的限制和约束。
对于全要素生产率的估计,常用的参数方法有SFA模型,该模型通过估计线性模型,对效率进行测算。尽管线性模型形式较为简单,但通常存在模型误设定问题,难以保证真实模型中自变量对因变量的影响为线性形式。相较于SFA模型,GNR方法采用非参数估计方法,放宽了对生产函数模型形式的限制,估计的生产函数更加贴合企业的实际生产过程。因此,研究采用GNR非参数生产函数模型估计高新技术企业的全要素生产率。
常用非参数方法有DEA模型,该模型可被应用于多投入与多产出的场景,通过计算每个决策单元投入产出权重,确定有效生产前沿面。DEA方法忽略了企业实际生产过程中要素投入决策与产出的时间差异性以及由此导致的内生性问题,相较于DEA模型,GNR方法可以更好地通过构建中间投入转换方程来解决内生性问题,并且对随机干扰项进行了更细致的区分,进而得到全要素生产率。
针对传导偏差和变量选择问题,GNR方法使用的是非参数识别和估计策略,放松了线性条件对于估计过程的限制,同时该策略不依赖要素价格外生变化的可获得性。此外,该模型因变量的选取,区别以往大部分文献所采用的增加值指标,从总量的角度衡量企业的总产出。故研究参照GNR方法,对生产过程采用非参数的形式进行描述,减少了模型设定对生产函数估计的影响[2]2973-3016。
为了刻画企业投入与产出之间的关系,构建生产函数模型
$$ \begin{array}{c}{Y}_{jt}=F({k}_{jt},{l}_{jt},{m}_{jt}){e}^{{v}_{jt}}= > {y}_{jt}=f({k}_{jt},{l}_{jt},{m}_{jt})+{v}_{jt}\end{array} $$ (1) 式中:大写变量为原函数形式,小写变量为对函数进行对数运算;j为第j个企业,t为年份;
$ {y}_{jt} $ 为企业总产出的对数形式;$ {k}_{jt} $ 为企业资本的对数形式;$ {l}_{jt} $ 为企业劳动的对数形式;$ {m}_{jt} $ 为企业中间投入的对数;$ {v}_{jt} $ 为希克斯中性全要素生产率冲击。将
$ {v}_{jt} $ 分解为$ {\omega }_{jt} $ 和$ {\varepsilon }_{jt} $ 。$ {\omega }_{jt} $ 为研究重点关注的全要素生产率,即对企业的生产决策和未来发展具有持续性影响的全要素生产率。对企业而言,其数值在作下一期的生产决策时是可以提前知晓的;但对研究者而言,其数值是未知的。$ {\varepsilon }_{jt} $ 为外生的全要素生产率冲击,与本期投入要素的决策相独立。对在研究过程中不可测的全要素生产率$ {\omega }_{jt} $ ,利用中间投入作为代理变量对其进行转换,由函数$ {M}_{t}\left(\cdot\right) $ 描述其关系,且该函数与时期相关。该变量的类型是不受约束的,即在企业作生产决策时不可被提前预知且与其滞后项之间相互独立,二者之间的具体关系为$$ \begin{array}{c}{m}_{jt}={M}_{t}({k}_{jt},{l}_{jt},{\omega }_{jt})\end{array} $$ (2) 同时,全要素生产率
$ {\omega }_{jt} $ 满足一阶马尔科夫过程,可得$$ \begin{array}{c}{\omega }_{jt}=h({\omega }_{jt-1})+{\eta }_{jt}={{\delta }_{0}+{\delta }_{1}\omega }_{jt-1}+{\eta }_{jt}\end{array} $$ (3) 式中:
$ h({\omega }_{jt-1}) $ 为一阶马尔科夫过程,$ \delta $ 为一阶展开系数,$ \eta_{it} $ 为误差项。在估计过程中,利用企业利润最大化这一准则来构建一阶条件方程
$$ \begin{array}{c}\underset{{M}_{\mathit{jt}}}{\mathrm{max}}{P}_{t}E[F({k}_{jt},{l}_{jt},{m}_{jt})]{e}^{{\omega }_{jt}+{\varepsilon }_{jt}}|{\Gamma }_{jt}]-{\rho }_{t}{M}_{jt}\end{array} $$ (4) 式中:
$ {P}_{t} $ 为市场公允的产出价格;$ E[F({k}_{jt},{l}_{jt},{m}_{jt})]{e}^{{\omega }_{jt}+{\varepsilon }_{jt}}|{\Gamma }_{jt}] $ 为给定企业j在第t期,企业总产出的数学期望;$ {P}_{t}E[F({k}_{jt},{l}_{jt},{m}_{jt})]{e}^{{\omega }_{jt}+{\varepsilon }_{jt}}|{\Gamma }_{jt}] $ 为企业总产出的价值;$ {\rho }_{t} $ 为市场公允的中间投入价格;$ {\rho }_{t}{M}_{jt} $ 为中间投入的价值;$ {\Gamma }_{jt} $ 为企业$ j $ 在第$ t $ 期作生产决策时已知的信息集,其一阶条件为$$ {P}_{t}\frac{\partial f({k}_{jt},{l}_{jt},{m}_{jt})}{\partial {M}_{jt}}{e}^{{\omega }_{jt}}\varepsilon ={\rho }_{t}$$ (5) 式中:设定
$ \varepsilon =E\left[{e}^{{\varepsilon }_{jt}}\right|{\mathrm{\Gamma }}_{jt}] $ ,表示给定企业j在第t期全要素生产率冲击的数学期望。通过对式(5)进行对数运算,可得
$${s}_{jt}={\mathrm{ln}}\varepsilon +\mathrm{ln}\left[\frac{\partial f({k}_{jt},{l}_{jt},{m}_{jt})}{\partial {m}_{jt}}\right]-{\varepsilon }_{jt}\equiv {\mathrm{ln}}{D}^{\mathit{\varepsilon }}({k}_{jt},{l}_{jt},{m}_{jt})-{\varepsilon }_{jt} $$ (6) 式中:
$ {s}_{jt}\equiv \mathrm{l}\mathrm{n}\left(\dfrac{{\rho }_{t}{M}_{jt}}{{P}_{t}{Y}_{jt}}\right) $ 为中间投入占总产出份额的对数形式;$ D({k}_{jt},{l}_{jt},{m}_{jt}) $ 为$ f({k}_{jt},{l}_{jt},{m}_{jt}) $ 对$ {m}_{jt} $ 的偏导,即$ \dfrac{\partial f({k}_{jt},{l}_{jt},{m}_{jt})}{\partial {m}_{jt}} $ ;$ {\varepsilon }_{jt} $ 为误差项。在第一阶段对式(6)进行非参数估计,从而得到对$ {D}^{\mathit{\varepsilon }}({k}_{jt},{l}_{jt},{m}_{jt}) \equiv$ $ \dfrac{D({k}_{jt},{l}_{jt},{m}_{jt})}{\mathit{\varepsilon }} $ 的估计。然而,由于函数
$ f(\cdot) $ 和$ h(\cdot) $ 均与企业的资本、劳动和中间投入有关,故在本阶段无法对其有效识别。在第一阶段的结果基础上,运用全要素生产率的一阶马尔科夫条件开展第二阶段的估计,从而得到各投入要素的产出弹性以及企业层面的全要素生产率。(二) 生产函数模型估计方法
在确定生产函数模型的形式后,将通过非参数估计方法对投入要素的产出弹性和企业层面的全要素生产率进行估计。在生产函数识别过程中,关键难题是企业通常会根据其自身的全要素生产率来选择最适合的投入数量,但对学者而言,企业的生产率是未知的,因此会产生内生性问题。现有研究主要采用两种方法减少内生性对估计的影响:第一种是采用标准的计量经济学理论方法,如使用固定效应或工具变量等,但该理论在实践中的应用有待进一步研究;第二种是采用静态一阶条件进行输入选择,该指数方法通过每种投入的产出弹性与其投入份额来恢复并估计生产函数和生产率,但是当某些投入受到调整摩擦的影响时,如资本成本、劳动雇佣成本的调整等,这些静态一阶条件就不再有效。研究采用GNR方法,充分考虑内生性问题,利用中间投入构建转换方程。为此,将估计的过程分为两个阶段。
第一阶段估计,通过利润最大化条件得到
$ {M}_{t}\left(\cdot\right) $ 的形式,将$ {m}_{jt} $ 表示为$$ {m}_{jt}={M}_{t}({k}_{jt},{l}_{jt},{\omega }_{jt})=M({k}_{jt},{l}_{jt},{\omega }_{jt}-{d}_{t})$$ (7) 式中:提取
$ {d}_{t}=\mathrm{ln}\left(\dfrac{{\rho }_{t}}{{P}_{t}}\right)-\mathrm{l}\mathrm{n}\mathit{\varepsilon } $ ,$ {d}_{t} $ 为仅与时期相关的部分。对式(7)两边取逆,将
$ {\omega }_{jt} $ 通过要素投入表示,代入式(1)中,可得$$\begin{split} E[{y}_{jt}|{k}_{jt},{l}_{jt},{m}_{jt},{d}_{t}]&=f({k}_{jt},{l}_{jt},{m}_{jt})+{M}^{-1}({k}_{jt},{l}_{jt},{m}_{jt})+{d}_{t}\\ &\equiv \phi ({k}_{jt},{l}_{jt},{m}_{jt})+{d}_{t} \end{split}$$ (8) 设定
$ \phi \left(\cdot\right) $ 为提取$ {d}_{t} $ 后剩下部分的函数,根据以上假设条件,可将总产出进一步表示为$$\begin{split} {y}_{jt}=&f({k}_{jt},{l}_{jt},{m}_{jt})+h[\phi ({k}_{jt-1},{l}_{jt-1},{m}_{jt-1})+{d}_{t-1}-\\ &f({k}_{jt-1},{l}_{jt-1},{m}_{jt-1})]+{\eta }_{jt}+{\varepsilon }_{jt} \end{split} $$ (9) 由于
$ f\left(\cdot\right) $ 和$ {M}^{-1}\left(\cdot\right) $ 都与$ {k}_{jt}\mathrm{、}{l}_{jt}\mathrm{、}{m}_{jt} $ 相关,故无法在第一阶段将这两个函数识别出来。同时,根据函数$ M\left(\cdot\right) $ 的设定形式,在式(9)中$ {m}_{jt} $ 与${\varepsilon }_{jt} $ 之间存在内生性问题。因此,如果利用该式进行估计,将无法保证估计量的一致性,导致无法对生产函数进行有效估计。但是,可通过多项式逼近方法将式(6)中的
$ {D}^{\mathit{\varepsilon }}({k}_{jt},{l}_{jt},{m}_{jt}) $ 识别出来,同时得到残差项$ {\varepsilon }_{jt} $ ,根据Chen对大样本下非参数方法得到的估计量性质,在该条件下多项式展开系数的估计量具有一致渐进正态性[15]。鉴于现有研究对估计量的性质分析以及估计模型的简洁性,将所有多项式展开的阶数设定为二阶,故$ {D}^{\mathit{\varepsilon }}(\cdot) $ 的展开式为$${D}^{\mathit{\varepsilon }}({k}_{jt},{l}_{jt},{m}_{jt})=\sum _{{r}_{k}+{r}_{l}+{r}_{m}\le 2}{{\gamma }_{{r}_{k},{r}_{l},{r}_{m}}'k}_{jt}^{{r}_{k}}{l}_{jt}^{{r}_{l}}{m}_{jt}^{{r}_{m}}$$ (10) 式中:
$ {\gamma }_{{r}_{k},{r}_{l},{r}_{m}}' $ 为多项式展开系数;$ {r}_{k} $ ,${r}_{l} $ ,${r}_{m} $ 为多项式展开阶数。通过样本平均得到
$ \mathit{\varepsilon } $ 的估计值$ \widehat{\mathit{\varepsilon }}=\displaystyle\frac{1}{JT}\sum_{j,t}{e}^{\widehat{{\varepsilon }_{jt}}} $ (J为企业总数,T为总年份数),在对式(10)两边进行积分并调整系数后,可得对$ D^{\varepsilon}(\cdot) $ 积分后的展开式$$\int D^{\varepsilon}({k}_{jt},{l}_{jt},{m}_{jt})d{m}_{jt}=\sum _{{r}_{k}+{r}_{l}+{r}_{m}\le 2}\frac{{\gamma }_{{r}_{k},{r}_{l},{r}_{m}}}{\left({r}_{m}+1\right)}{k}_{jt}^{{r}_{k}}{l}_{jt}^{{r}_{l}}{m}_{jt}^{{r}_{m}+1} $$ (11) 设定
$ \widehat{\gamma }=\dfrac{{\widehat{\gamma }}'}{\widehat{\mathit{\varepsilon }}} $ ,对式(11)的系数进行估计,可得$$ \int \frac{\partial f({k}_{jt},{l}_{jt},{m}_{jt})}{\partial {m}_{jt}}d{m}_{jt}=f({k}_{jt},{l}_{jt},{m}_{jt})+\varrho ({k}_{jt},{l}_{jt})$$ (12) 从而完成第一阶段的估计。
第二阶段的估计主要在第一阶段的基础上,利用
$ {\omega }_{jt} $ 的一阶马尔科夫过程进行下一步的识别。积分后,为了估计式(12)右式中的函数$ \varrho (\cdot) $ ,对其进行多项式逼近,同样采用二阶的形式进行展开$$ \varrho ({k}_{jt},{l}_{jt})=\sum _{{0 < \tau }_{k}+{\tau }_{l}\le 2}{\alpha }_{{\tau }_{k},{\tau }_{l}}{k}_{jt}^{{\tau }_{k}}{l}_{jt}^{{\tau }_{l}} $$ (13) 式中:
${\alpha }_{{\tau }_{k},{\tau }_{l}} $ 为多项式展开系数,利用数据估计得到具体的数值;${{\tau }_{k},{\tau }_{l}} $ 为资本和劳动对应的指数,$ {\tau }_{k},{\tau }_{l}\ge 0 $ 。同时,根据第一阶段估计结果,可得
$${\mathcal{Y}}_{jt}\equiv {y}_{jt}-{\varepsilon }_{jt}-\int \frac{\partial f({k}_{jt},{l}_{jt},{m}_{jt})}{\partial {m}_{jt}}d{m}_{jt}=-\varrho ({k}_{jt},{l}_{jt})+{\omega }_{jt}$$ (14) 在此基础上,利用一阶马尔科夫条件,构建第一阶段和第二阶段的矩条件,利用GMM方法完成GNR两阶段非参数估计,可得
$$ \left\{\begin{array}{c}E\left[{\varepsilon }_{jt}\dfrac{\partial \mathrm{l}\mathrm{n}D^{\varepsilon}({k}_{jt},{l}_{jt},{m}_{jt})}{\partial \gamma }\right]=0\\ E[{\eta }_{jt}{k}_{jt}^{{\tau }_{k}}{l}_{jt}^{{\tau }_{l}}]=0\\ E[{\eta }_{jt}{\mathcal{Y}}_{jt-1}]=0\end{array}\right. $$ (15) 参考Horowitz的研究,通过Bootstrap可以计算得到生产函数模型估计系数的标准差[16]。
四、 中国高新技术企业的投入与产出数据处理
(一) 数据来源
研究主要针对中国高新区企业的生产函数和全要素生产率进行估计与分析,将科技部火炬高技术产业开发中心发布的国家高新区和高新技术企业统计调查数据作为原始数据集。该数据集中包含了中国A、B、C三座城市共6 923家高新区内企业的样本,时间区间为2013—2019年,包括21 000余个样本点。同时,数据集覆盖了企业的基本情况、财务指标、人员概况、科技情况等方面的信息,涵盖了8个高新技术领域和200余个小领域。
原始数据集是由3座城市分别统计的高新技术企业信息,由于时间和地域等因素的影响,3个数据集在变量统计范围和指标命名方式上有较大的差异。因此,需要先根据统计指标的经济学含义,对3个小数据集的命名方式进行统一,并将3个地区的数据集以一定的标准和规范合并成一个完整的、可分析的全数据集,再开展进一步的数据清洗和变量筛选工作。最终,得到的数据集包含6 923家企业的21 549个样本观测,共362个指标。
(二) 产出与投入指标选取
研究根据企业生产过程要求,选取以下指标来衡量企业的总产出以及投入要素投入。结合高新技术企业高投入、高风险和高产出等发展特征,选取“营业收入”“主营业务收入”“技术收入”“产品销售收入”衡量企业的总产出(gross output,Y)
④ ;使用“固定资产合计”衡量资本存量(capital,K),使用“从业人员年平均人数”衡量劳动(labor,L)。在GNR方法中,通过引入中间投入变量、构建中间投入转换方程,有效地降低了内生性对估计的影响。根据Gandhi的研究[2]2973-3016,在衡量方式上,中间投入表示为原材料、能源(燃料加电力)和服务支出的总和。针对高新技术企业,发现超过50%的企业为电子与信息领域,在高技术生产过程中,大多数的产出源于计算机、研究仪器等设备,中间投入为这些硬件、软件设备所消耗的能量,涉及原材料和服务的支出较小。因此,使用“综合能源消费量”衡量中间投入(intermediate input,M),该指标单位以吨(标准煤)计算。对于工业企业,该变量统计主要包括其在生产活动中涉及的各类能源;对于非工业企业,主要包括用于新技术研究等方面的能源。
(三) 样本筛选
按照以下规则剔除不满足要求的样本和公司[17-18]:一是企业的营业收入小于当年的主营业务收入;二是企业的营业收入不等于当年技术收入、产品销售收入、商品销售收入与企业营业收入之和;三是产品销售收入小于高新技术产品。
为了确保估计的可行与结果的可靠,剔除了在数据集中只有一年记录的公司和记录年份不连续的企业,从而减少数据的调查统计过程对生产函数估计结果产生的影响,并且剔除了劳动小于等于10人、固定资产净值小于1万元的企业[2]2973-3016[19]。根据《国家高新区和高新技术企业统计调查制度》
⑤ 中对企业所属技术领域的分类规定,提取了每个企业所属的技术领域信息,取其3位码的首位作为该公司所属技术领域的1位码,从中选取出了四大技术领域(1位码)作为样本总体。其中,1为电子与信息领域,2为生物医药领域,3为新材料领域,4为光机电一体化领域。最终数据集包括8 306个样本点,覆盖了2 099家高新技术产业开发区内的企业。(四) 变量处理
对于资本存量,根据2017年发布的统计报表制度、2019年发布的国家高新区企业统计调查制度中对固定资产净值衡量指标的描述,将2019版本企业经济概况中的变量“固定资产净值”和2017版本中的“固定资产合计”进行合并,得到没有缺失值的新变量“固定资产合计”。将该变量作为企业的资本存量,单位以当年价格(千元)统计。
对于总产出中的“营业收入”“主营业务收入”“技术收入”和“产品销售收入”指标,以2010年为基期计算不变价,使用国家统计局发布的GDP平减指数进行平减;对于资本存量,使用国家统计局发布的固定资产投资价格指数进行平减;对于中间投入的价值,采用2010年环渤海动力煤(5 500大卡)综合平均价格进行计算。
(五) 描述性统计
经过上述数据清洗和变量筛选后,总体样本包括了A、B、C三个地区的共计2 099家高新技术企业,涉及四大技术领域。企业存续情况,如表1所示。由此可知,约52%的企业在2008年后注册成立,这可能与2008年实施的《高新技术企业认定管理办法》(国科发火〔2008〕172号)存在紧密关联。
表 1 企业注册年份分布情况注册时间 2003年以前 2003—2007年 2008—2012年 2013—2017年 企业数目 405 588 646 460 样本数目 1 832 2 520 2 631 1 323 根据企业注册时间,计算得到企业存续情况,如图1所示。由图1可知,成立时间在10年内的企业,在本数据集的占比超过50%,在样本观察区间内企业的平均存续年限约为4年,94家企业存续时间超过了20年。企业存续时间整体呈右偏分布。
在此基础上,将总体样本划分成制造型企业和服务型企业。其中,制造型企业代表存续年份具有工业总产值且数值较大的公司,占总体样本的52%,共有1 098家企业。高新技术企业样本的具体分布情况,如表2所示。由表2可知,A地区和C地区以制造业为主,A地区的制造型企业占比超过60%,B地区企业以服务型企业为主。此外,A、B、C地区的高新技术企业所属技术涉及电子和信息领域较多,占比均超过了样本的50%。
表 2 高新技术企业样本的分布情况统计对象 地区分布 企业所属技术领域分类 汇总 电子与信息 生物医药技术 新材料 光机电一体化 公司数 样本数 公司数 样本数 公司数 样本数 公司数 样本数 公司数 样本数 总体样本 A地区 506 1813 111 407 150 560 263 950 1030 3730 B地区 733 3017 102 463 30 156 85 345 950 3981 C地区 60 300 26 130 14 70 19 95 119 595 汇总 1299 5130 239 1000 194 786 367 1390 2099 8306 制造型企业 A地区 215 809 50 182 142 532 257 930 664 2453 B地区 196 881 72 345 29 150 74 311 371 1687 C地区 21 105 14 70 12 60 16 80 63 315 汇总 432 1795 136 597 183 742 347 1321 1098 4455 服务型企业 A地区 291 1004 61 225 8 28 6 20 366 1277 B地区 537 2136 30 118 1 6 11 34 579 2294 C地区 39 195 12 60 2 10 3 15 56 280 汇总 867 3335 103 403 11 44 20 69 1001 3851 利用价格指数平减后的常用总产出衡量指标对数形式的统计特征,如表3所示。由表3可知,样本中既包括规模较大、成立时间较长的企业,也包括成立时间较短的初创公司。不同企业总产出变量存在一定差异,这一差异也体现在不同地区之间,即C地区企业间差距较小,B地区相对较大。投入要素的描述性统计,如表4所示。其中,所有数据都代表经平减后的原始数据对数形式。由表4可知,对高新技术企业而言,其使用到的中间投入较少,资本和劳动仍然是最主要的投入要素。
表 3 高新技术企业总产出指标的统计描述总产出衡量指标 变量名称 地区分布 最小值 下四分位数 中位数 均值 上四分位数 最大值 营业收入/千元 y1 A地区 2.369 8.895 10.203 10.218 11.630 16.480 B地区 2.753 8.508 9.604 9.735 10.883 17.949 C地区 4.632 9.222 10.256 10.384 11.366 15.991 汇总 2.369 8.725 9.906 9.998 11.273 17.949 主营业务收入/千元 y2 A地区 −0.579 8.860 10.178 10.166 11.609 16.426 B地区 −0.314 8.456 9.579 9.656 10.867 17.944 C地区 4.619 9.177 10.218 10.351 11.351 15.991 汇总 −0.579 8.678 9.881 9.935 11.250 17.944 技术收入/千元 y3 A地区 −0.579 −0.514 −0.382 2.860 7.441 14.945 B地区 −0.579 −0.243 7.404 5.802 9.145 16.099 C地区 −0.637 −0.514 −0.382 3.479 7.403 14.889 汇总 −0.637 −0.448 5.256 4.314 8.520 16.099 产品销售收入/千元 y4 A地区 −0.579 7.423 9.832 8.518 11.466 16.026 B地区 −0.579 −0.382 8.121 6.236 10.142 17.927 C地区 −0.637 8.259 9.834 9.183 11.132 15.991 汇总 −0.637 4.856 9.045 7.472 10.956 17.927 表 4 主要解释变量的统计描述投入要素指标 变量名称 地区分布 最小值 下四分位数 中位数 均值 上四分位数 最大值 资本存量/千元 k A地区 1.764 6.537 8.250 8.369 10.155 16.220 B地区 1.528 5.744 7.383 7.571 9.263 16.491 C地区 2.009 6.474 8.083 8.298 10.212 14.424 汇总 1.528 6.126 7.806 7.982 9.758 16.491 劳动/人 l A地区 2.398 3.401 4.248 4.357 5.080 8.613 B地区 2.398 3.401 4.111 4.327 5.030 10.569 C地区 2.398 3.689 4.382 4.581 5.323 8.666 汇总 2.398 3.401 4.190 4.359 5.081 10.569 中间投入/千元 m A地区 −0.322 −0.322 −0.322 2.077 4.819 12.553 B地区 −0.322 −0.322 −0.322 1.174 2.370 14.112 C地区 −0.322 −0.322 −0.322 2.146 4.602 9.956 汇总 −0.322 −0.322 −0.322 1.649 3.898 14.112 五、 中国高新技术企业的生产函数估计
(一) 基于全样本的生产函数估计
针对全样本数据集,构建高新技术企业非参数生产函数模型,并利用GNR方法对模型进行估计与分析。
1. 各投入要素产出弹性的估计
使用资本、劳动和中间投入作为高新技术企业的投入要素,利用研究中常使用的 “营业收入”“主营业务收入”来衡量总产出等指标,得到各投入要素的平均产出弹性,如表5所示。鉴于企业生产过程的异质性,投入要素的弹性系数代表各企业产出弹性的均值,资本强度(相对于劳动力)则代表了平均资本产出弹性与平均劳动产出弹性的比率。
表 5 全样本弹性系数的估计结果弹性系数 总产出的衡量指标 营业收入 主营业务收入 劳动 0.4334 0.4589 资本存量 0.2259 0.1979 中间投入 0.0001 0.0001 总和 0.6594 0.6569 资本强度 0.5212 0.4311 注:“总和” 表示劳动、资本、中间投入弹性系数之和;“资本强度”表示资本弹性系数与劳动弹性系数之商。表6同。 由表5可知,根据生产函数的弹性系数估计结果,在所有企业的平均水平上,对营业收入、主营业务收入而言,其资本的产出弹性都小于劳动的产出弹性,即资本强度小于1。结果表明,相较资本,劳动对总产出的贡献更加显著,即增加劳动更有助于总产出的提升。同时,由于高新技术企业具有从事高技术生产或服务的特性,可以发现,高新技术企业的主要投入要素为资本和劳动,对于综合能源消费量的消耗和依赖性较低,即投入要素弹性系数存在较强的异质性,中间投入弹性系数相对劳动和资本存量较小。营业收入和主营业务收入的估计结果基本具有一致性,但前者的资本强度更高。这说明,高新技术企业的营业收入对资本更为敏感。纵向来看,营业收入和主营业务收入的产出弹性系数的总和均小于1,即存在规模报酬递减。
2. 总产出随要素投入的变化趋势
针对估计得到的生产函数,绘制了总产出
$ \widehat{f({k}_{jt},{l}_{jt},{m}_{jt})} $ 随资本、劳动和中间投入的变化趋势。全样本下总产出随要素投入的变化趋势,如图2所示。由于$ \widehat{f} $ 的计算与三种投入的取值相关,故在考察$ \widehat{f} $ 随单个投入变化的趋势时,选取样本平均值作为另外两种投入的表示形式,从而得到$ \widehat{f} $ 受单个投入影响的变化趋势,即该趋势描述了在样本平均水平时企业生产过程随要素投入的变化规律。图2(a)的横轴代表资本,范围为样本中
$ k $ 的最小值到最大值。由图2(a)可知,对主营业务收入而言,$ \widehat{f} $ 对$ k $ 斜率逐渐减小,即边际产出是递减的。从产业层面来分析,高新技术企业把自身拥有的高新技术融合到了生产的产品和服务中,随着产成品以及服务活动流入市场,对高技术产业发展和宏观经济增长起到推动作用,这也是中国大力支持企业创新、推动产业升级的重要原因之一。图2(b)的横轴代表劳动,表示当资本投入和中间投入处于样本平均水平时,劳动对企业总产出的影响。由图2(b)可知,高新技术企业主营业务收入劳动的边际产出均呈现递减的状态。这意味着,对中国多数高新技术企业而言,不需要过多的劳动参与。而当劳动水平达到一定人数时,对企业的总产出产生抑制作用,显示了高新技术产业并非传统的劳动密集型产业。上述估计结果还发现,总产出几乎不随中间投入的增加而增加。对于高新技术企业,中间投入的增加不会对企业总产出产生显著的影响。高新技术产业涉及电子与信息领域的高新技术企业占比较高,在这类企业的投入产出过程中,不需要过多的能源消耗,与上文所呈现的高新技术企业中间投入较小的趋势一致。因此,中间投入不会对企业的总产出产生较大的正向或负向影响,符合先前的预期与数据集中高新技术企业的实际情况。
(二) 不同行业的高新技术企业生产函数估计
鉴于不同行业的企业生产过程特征有所区别,仅使用全样本进行估计无法完全反映各行业的投入产出特征,故对样本企业所属类型进行划分。将高新技术企业分成制造型企业和服务型企业两类,利用GNR两阶段非参数估计对它们的生产函数分别进行估计,得到不同行业的生产函数,从而比较不同行业中高新技术企业生产函数的异同,并进一步分析其生产过程的异质性。
1. 制造型高新技术企业的生产函数估计
通过GNR两阶段非参数估计得到生产函数模型的系数,根据得到的估计系数,计算企业投入要素的平均产出弹性。参照Gandhi等学者的研究[2]2973-3016,该产出弹性代表了样本集企业层面的平均水平,具体结果,如表6所示。
表 6 制造型高新技术企业弹性系数的估计结果弹性系数 总产出的衡量指标 营业收入 主营业务收入 产品销售收入 劳动 0.5973 0.5843 0.5822 资本存量 0.7197 1.1482 1.0825 中间投入 0.0001 0.0001 0.0001 总和 1.3170 1.7325 1.6648 资本强度 1.2049 1.9652 1.8593 由表6可知,从横向来看,在营业收入、主营业务收入和产品销售收入作为总产出衡量指标下,制造型企业的生产函数均表现为规模报酬递增,即表中“总和”项均大于1。主营业务收入和产品销售收入的各项投入弹性系数基本一致,二者的资本弹性系数显著大于营业收入的资本弹性系数。这说明,在整体层面,资本投入可以促进制造型高新技术企业形成自身的固定资产。根据制造业的生产特性,企业可以利用自己的建筑、设备等固定资产扩大生产规模,增加企业的产品产出和销售,从而提高主营业务收入。
制造型企业的总产出随要素投入的变化趋势,如图3所示。
由图3(a)和图3(c)可知,分析总产出随资本投入的变化趋势,与全样本的结果不同,主营业务收入下资本的边际产出是递增的。该结果与制造业的特点相吻合,即利用大量的资本投入形成企业的固定资本,通过厂房扩建、使用智能设备等形式扩大企业生产规模、提升企业生产效率,从而增加主营业务收入,实现企业利润最大化。这一特点也可以从产品销售收入随资本变化的趋势得到进一步验证,即随着资本的不断投入,制造业企业会生产更多的产品(包括高新技术产品),而后通过销售产品进行盈利。
由图3(b)和图3(d)可知,总产出随劳动投入的变化趋势,变化趋势和全样本基本保持一致。对主营业务收入和产品销售收入而言,劳动的投入均呈现边际规模递减的趋势,在其他条件保持不变的情况下,当企业从业人员达到一定水平时,企业的边际产出会有所下降。
总产出随中间投入的变化趋势和全样本基本一致,中间投入的变化并不会显著影响企业的总产出。对高新技术制造型企业而言,其总产出并不像传统制造业企业一样很大程度上依赖中间投入的价值,而是利用先进的生产手段提升生产效率,增加公司的总产出,从而提升企业的经济效益。
2. 服务型高新技术企业的生产函数估计
通过生产函数计算各投入要素的弹性系数发现,服务业的弹性系数与制造业存在一定的差距,但资本投入对企业总产出的贡献仍然大于劳动投入的贡献。在其他投入要素处于样本平均水平的情况下,计算总产出随单一投入要素的变化趋势,如图4所示。
首先,分析总产出随单一投入要素的变化趋势。对资本而言,主营业务收入和技术收入随资本变化的趋势基本一致,即在其他要素保持平均水平下,存在边际产出递减的现象。对于劳动,在主营业务收入下,劳动的边际产出呈现了一种递减的趋势,与全样本和制造型企业所展现的结果相一致。此外,在服务型企业中,中间投入对总产出的影响依然不显著。
其次,针对服务业生产特性,进一步选择技术收入作为企业总产出,估计得到生产函数,其结果与上述情况无显著差异。对以服务为主的高新技术企业而言,资本和劳动的投入均存在边际递减的特征,且在本数据集内存在拐点。这表明,在平均水平下,当企业规模较小时,增加资本和劳动的投入会提升企业的总产出,但是当企业规模增加到一定程度时,总产出的提升更依赖全要素生产率的提高,而不是投入要素规模的增加。
最后,通过对比制造型高新技术企业和服务型高新技术企业发现:制造型企业主要通过将高新技术融入产品的生产过程,通过销售新产品实现其经营目标,资本投入的增加会大幅提升企业的总产出。对服务型企业而言,在平均水平下,资本和劳动均存在边际产出递减,且产出的增加对资本的投入更加敏感。
六、 中国高新技术企业的全要素生产率分析
下文将估计每个企业在每一存续年份的全要素生产率,同时将利用核密度估计得到不同行业全要素生产率的分布情况,并进一步比较和讨论不同领域和不同对外贸易类型的企业全要素生产率分布特征。
(一) 基于不同行业的高新技术企业全要素生产率分析
1. 制造型企业的全要素生产率分析
选择正态核函数进行核密度估计,得到全要素生产率概率密度,如图5所示。
针对制造型企业,采用主营业务收入和产品销售收入两个指标来衡量企业总产出。图5(a)表示在主营业务收入下的全要素生产率分布,均值集中在0附近。这表明,在当前发展阶段,企业的生产过程并没有通过全要素生产率的提高得到效率上的提升。图5(b)表示产品销售收入下的全要素生产率分布,大部分企业的全要素生产率水平处于较低的状态。这表明,企业总产出的提升仍处于初始阶段,即依赖要素投入的积累。
由图5可知,主营业务收入与产品销售收入得到的全要素生产率分布较为一致,与行业特点相吻合,即制造型高新技术企业普遍通过生产、销售产成品完成企业经营目标。
2. 服务型企业的全要素生产率分析
根据模型估计结果,绘制各个总产出衡量指标下的服务型高新技术企业全要素生产率的分布,如图6所示。
相较于制造型企业,服务型企业的全要素生产率的分布呈现右偏的趋势。对主营业务收入而言,服务型企业的全要素生产率平均水平较高,说明企业的高新技术、公司治理、资源配置等能力会提高要素投入转化为企业总产出的整体效率,从而促进服务型高新技术企业的成长发展。对技术收入而言,由于样本内企业普遍成立时间较短,仍处于初创期,总产出的提高整体上主要依赖各类资源的投入和积累,而非企业全要素生产率的提高。
通过比较发现,不同行业企业的全要素生产率存在异质性。对制造型企业而言,全要素生产率分布较集中,行业发展相对成熟,但是对于初创企业,仍主要依赖要素投入;而对服务型企业而言,行业内企业存在较大的差异,发展情况和发展阶段较分散。
(二) 全要素生产率的其他分析
1. 不同领域的全要素生产率比较
分别统计电子信息、生物医药、新材料和光机电一体化领域企业的平均全要素生产率,以分析不同技术领域下,企业全要素生产率的异质性。
首先,对全样本下的全要素生产率进行比较。营业收入下全要素生产率的概率密度,如图7所示。由图7可知,不同技术领域间的全要素生产率存在异质性,其中电子与信息领域的全要素生产率比较集中,领域内企业的差异性较小。
同时,对全样本中不同领域的平均全要素生产率进行了排序,如表7所示。结果表明,新材料领域的全要素生产率显著高于其他领域,说明对于该行业来说,企业的全要素生产率对提升技术服务和产成品的产出有促进作用,并且在营业收入、主营业务收入、技术收入和产品销售收入这4个指标衡量下的结果具有一致性。
表 7 全样本下各领域的全要素生产率排序技术领域 总产出衡量指标排序 营业收入 主营业务收入 技术收入 产品销售收入 1电子与信息 4 4 4 4 2生物与医药 3 3 3 3 3新材料 1 1 1 1 4光机电一体化 2 2 2 2 其次,对制造型高新技术企业的全要素生产率进行比较。对不同领域企业的全要素生产率排序结果,如表8所示。结果表明,新材料领域较其他领域的全要素生产率最高,光机电一体化领域的全要素生产率最低,不同领域企业间的生产过程和策略存在异质性。此外,营业收入、主营业务收入与产品销售收入排序结果具有一致性。
表 8 制造型企业各领域的全要素生产率排序技术领域 总产出衡量指标排序 营业收入 主营业务收入 产品销售收入 1电子与信息 3 3 3 2生物与医药 2 2 2 3新材料 1 1 1 4光机电一体化 4 4 4 最后,对服务型高新技术企业的全要素生产率进行比较。全要素生产率均值的排序结果,如表9所示。结果表明,营业收入、主营业务收入的结果具有一致性,对于新材料领域的服务型高新技术企业而言,全要素生产率的提升主要体现在技术研发上,而光机电一体化的领域企业的全要素生产率主要体现在产品的销售与服务提升上,该结果说明,不同领域之间服务型高新技术企业的全要素生产率存在异质性。
表 9 服务型企业各领域的全要素生产率排序技术领域 总产出衡量指标排序 营业收入 主营业务收入 技术收入 1电子与信息 2 2 3 2生物与医药 4 4 4 3新材料 1 1 1 4光机电一体化 3 3 2 2. 进出口对全要素生产率的影响
在现有研究中,企业进出口类型对全要素生产率的影响是学者们比较关心的一个热点问题。戴觅等的研究发现,出口有利于企业全要素生产率的提升[20],张杰等利用中国制造业企业数据也印证了该结论[21],刘卉和王永进对出口类型进行了更细致的划分,发现直接出口企业的全要素生产率最高[22]。然而,也有研究表明,非出口企业反而具有更高的全要素生产率[23-25]。故根据进出口总额和出口总额指标,将样本划分为出口企业和非出口企业,进行更细致的分析。不同外贸类型高新技术企业的全要素生产率,如表10 所示。
表 10 不同外贸类型高新技术企业的全要素生产率总产出衡量指标 制造型企业 服务型企业 营业收入 产品销售收入 营业收入 技术收入 全要素生产率 出口 1.95 −2.44 0.62 −1.86 非出口 1.39 −3.58 0.59 −1.86 根据上述结果,其一,考察出口对制造型高新技术企业全要素生产率的影响发现:在营业收入下,出口企业比非出口企业全要素生产率高40%左右;在产品销售收入下,出口企业比非出口企业全要素生产率高32%左右。这与已有研究结果基本一致,即出口会提升制造型高新技术企业的生产效率,通过出口高技术产品提升企业绩效。其二,对服务型高新技术企业的全要素生产率进行比较发现:在营业收入和技术收入下,企业的外贸类型对于全要素生产率的估计无显著影响,即出口并没有提升服务型高新技术企业的全要素生产率。
通过对比发现:由于生产特点和企业经营策略的差异性,不同领域的企业全要素生产率存在一定的异质性。对于制造行业,出口类型的企业全要素生产率高于非出口型企业的平均全要素生产率水平;对于服务业,企业对外贸易类型对全要素生产率无显著影响。
七、 结论与启示
研究的创新及贡献主要体现在两个方面:一方面,描述并估计了中国高新技术企业的生产函数,采用科技部统计的国家高新区和高新技术企业微观数据,并充分考虑内生性和生产函数模型形式对估计过程的影响,采用非参数结构模型。根据高新区企业数据的特点与性质,采用GNR方法,估计得到中国高新技术企业的生产函数。另一方面,研究了中国高新技术企业的全要素生产率情况,估计了企业在每一存续年份的全要素生产率,通过核密度估计等非参数方法,比较制造型企业和服务型企业全要素生产率的异同点。
具体而言,研究主要从全要素生产率的角度研究高新技术企业的创新水平,分析高新技术企业推动新型工业化的作用。得出如下结论:
第一,从高新技术企业整体来看,利用营业收入和主营业务收入作为总产出,各投入要素对总产出的贡献无显著差异,技术收入和产品销售收入对资本投入比对劳动投入更加敏感。当其他投入要素处于样本平均水平时,劳动具有边际产出递减的特征。
第二,分别估计制造业企业和服务业企业的生产函数。对制造业而言,当分别采用主营业务收入和产品销售收入衡量企业总产出时,它们的投入要素平均产出弹性、总产出变化趋势基本一致,估计结果比较稳健;资本投入更大程度上提升了企业总产出,说明未来应该进一步加大对高新技术企业的投资,政府的科技投入资金可以用于提升企业的生产效率,促进企业的生产销售过程,从而更好地发挥高新技术企业的领跑作用,助推新型工业化的发展。
第三,制造型企业的全要素生产率较低,说明这类企业总产出的提高仍主要依赖资源投入,仍处于资源积累的发展阶段。对服务型企业而言,资本存量的弹性系数较大,材料领域的全要素生产率相对较高,且不同技术领域中的企业全要素生产率具有一定的异质性。要加快建立产学研相结合的体系框架,促进高新技术企业的科技研究成果落地与转化,增加国家高新区企业的产出效益,进而推动高新技术产业和宏观经济的高质量发展。
注释:
① 参见:国家高新技术产业开发区总数达178家,网址为https://www.gov.cn/lianbo/bumen/202312/content_6919803.htm。② 参见:国家统计局统计科学研究所所长闾海琪解读2023年我国经济发展新动能指数 ,网址为https://www.stats.gov.cn/sj/sjjd/202408/t20240831_1956157.html。③ 参见:湖北高新技术企业数量突破2.5万家,网址为https://www.most.gov.cn/dfkj/hub/zxdt/202404/t20240401_190054.html。⑤ 参见:国家高新区和高新技术企业统计调查制度 ,网址为https://www.stats.gov.cn/fw/bmdcxmsp/bmzd/202302/t20230215_1907184.html。 -
表 1 企业注册年份分布情况
注册时间 2003年以前 2003—2007年 2008—2012年 2013—2017年 企业数目 405 588 646 460 样本数目 1 832 2 520 2 631 1 323 表 2 高新技术企业样本的分布情况
统计对象 地区分布 企业所属技术领域分类 汇总 电子与信息 生物医药技术 新材料 光机电一体化 公司数 样本数 公司数 样本数 公司数 样本数 公司数 样本数 公司数 样本数 总体样本 A地区 506 1813 111 407 150 560 263 950 1030 3730 B地区 733 3017 102 463 30 156 85 345 950 3981 C地区 60 300 26 130 14 70 19 95 119 595 汇总 1299 5130 239 1000 194 786 367 1390 2099 8306 制造型企业 A地区 215 809 50 182 142 532 257 930 664 2453 B地区 196 881 72 345 29 150 74 311 371 1687 C地区 21 105 14 70 12 60 16 80 63 315 汇总 432 1795 136 597 183 742 347 1321 1098 4455 服务型企业 A地区 291 1004 61 225 8 28 6 20 366 1277 B地区 537 2136 30 118 1 6 11 34 579 2294 C地区 39 195 12 60 2 10 3 15 56 280 汇总 867 3335 103 403 11 44 20 69 1001 3851 表 3 高新技术企业总产出指标的统计描述
总产出衡量指标 变量名称 地区分布 最小值 下四分位数 中位数 均值 上四分位数 最大值 营业收入/千元 y1 A地区 2.369 8.895 10.203 10.218 11.630 16.480 B地区 2.753 8.508 9.604 9.735 10.883 17.949 C地区 4.632 9.222 10.256 10.384 11.366 15.991 汇总 2.369 8.725 9.906 9.998 11.273 17.949 主营业务收入/千元 y2 A地区 −0.579 8.860 10.178 10.166 11.609 16.426 B地区 −0.314 8.456 9.579 9.656 10.867 17.944 C地区 4.619 9.177 10.218 10.351 11.351 15.991 汇总 −0.579 8.678 9.881 9.935 11.250 17.944 技术收入/千元 y3 A地区 −0.579 −0.514 −0.382 2.860 7.441 14.945 B地区 −0.579 −0.243 7.404 5.802 9.145 16.099 C地区 −0.637 −0.514 −0.382 3.479 7.403 14.889 汇总 −0.637 −0.448 5.256 4.314 8.520 16.099 产品销售收入/千元 y4 A地区 −0.579 7.423 9.832 8.518 11.466 16.026 B地区 −0.579 −0.382 8.121 6.236 10.142 17.927 C地区 −0.637 8.259 9.834 9.183 11.132 15.991 汇总 −0.637 4.856 9.045 7.472 10.956 17.927 表 4 主要解释变量的统计描述
投入要素指标 变量名称 地区分布 最小值 下四分位数 中位数 均值 上四分位数 最大值 资本存量/千元 k A地区 1.764 6.537 8.250 8.369 10.155 16.220 B地区 1.528 5.744 7.383 7.571 9.263 16.491 C地区 2.009 6.474 8.083 8.298 10.212 14.424 汇总 1.528 6.126 7.806 7.982 9.758 16.491 劳动/人 l A地区 2.398 3.401 4.248 4.357 5.080 8.613 B地区 2.398 3.401 4.111 4.327 5.030 10.569 C地区 2.398 3.689 4.382 4.581 5.323 8.666 汇总 2.398 3.401 4.190 4.359 5.081 10.569 中间投入/千元 m A地区 −0.322 −0.322 −0.322 2.077 4.819 12.553 B地区 −0.322 −0.322 −0.322 1.174 2.370 14.112 C地区 −0.322 −0.322 −0.322 2.146 4.602 9.956 汇总 −0.322 −0.322 −0.322 1.649 3.898 14.112 表 5 全样本弹性系数的估计结果
弹性系数 总产出的衡量指标 营业收入 主营业务收入 劳动 0.4334 0.4589 资本存量 0.2259 0.1979 中间投入 0.0001 0.0001 总和 0.6594 0.6569 资本强度 0.5212 0.4311 注:“总和” 表示劳动、资本、中间投入弹性系数之和;“资本强度”表示资本弹性系数与劳动弹性系数之商。表6同。 表 6 制造型高新技术企业弹性系数的估计结果
弹性系数 总产出的衡量指标 营业收入 主营业务收入 产品销售收入 劳动 0.5973 0.5843 0.5822 资本存量 0.7197 1.1482 1.0825 中间投入 0.0001 0.0001 0.0001 总和 1.3170 1.7325 1.6648 资本强度 1.2049 1.9652 1.8593 表 7 全样本下各领域的全要素生产率排序
技术领域 总产出衡量指标排序 营业收入 主营业务收入 技术收入 产品销售收入 1电子与信息 4 4 4 4 2生物与医药 3 3 3 3 3新材料 1 1 1 1 4光机电一体化 2 2 2 2 表 8 制造型企业各领域的全要素生产率排序
技术领域 总产出衡量指标排序 营业收入 主营业务收入 产品销售收入 1电子与信息 3 3 3 2生物与医药 2 2 2 3新材料 1 1 1 4光机电一体化 4 4 4 表 9 服务型企业各领域的全要素生产率排序
技术领域 总产出衡量指标排序 营业收入 主营业务收入 技术收入 1电子与信息 2 2 3 2生物与医药 4 4 4 3新材料 1 1 1 4光机电一体化 3 3 2 表 10 不同外贸类型高新技术企业的全要素生产率
总产出衡量指标 制造型企业 服务型企业 营业收入 产品销售收入 营业收入 技术收入 全要素生产率 出口 1.95 −2.44 0.62 −1.86 非出口 1.39 −3.58 0.59 −1.86 -
[1] 习近平就推进新型工业化作出重要指示强调 把高质量发展的要求贯穿新型工业化全过程 为中国式现代化构筑强大物质技术基础[N]. 人民日报, 2023−09−24(4). [2] GANDHI A, NAVARRO S, RIVERS D A. On the identification of gross output production functions [J]. Journal of Political Economy, 2020, 128(8): 2973-3016.
[3] OLLEY G S, PAKES A. The dynamics of productivity in the telecommunications equipment industry [R]. Cambridge: National Bureau of Economic Research, 1992.
[4] LEVINSOHN J, PETRIN A. Estimating production functions using inputs to control for unobservables [J]. The Review of Economic Studies, 2003, 70(2): 317-341.
[5] ACKERBERG D, BENKARD C L, BERRY S. Econometric tools for analyzing market outcomes [J]. Handbook of Econometrics, 2007, 6: 4171-4276.
[6] WOOLDRIDGE J M. On estimating firm-level production functions using proxy variables to control for unobservables [J]. Economics Letters, 2009, 104(3): 112-114.
[7] GANDHI A, NAVARRO S, RIVERS D. How heterogeneous is productivity? A comparison of gross output and value added [R]. Ontario: Centre for Human Capital and Productivity (CHCP), 2017.
[8] 吴延兵, 米增渝. 创新、模仿与企业效率——来自制造业非国有企业的经验证据[J]. 中国社会科学, 2011(4): 77-94. [9] 黄先海, 金泽成, 余林微. 基于生产函数法的企业盈利能力估计及比较研究[J]. 统计研究, 2016, 33(6): 42-51. [10] 国家统计局国民经济核算司. 中国2012年投入产出表编制方法[M]. 北京: 中国统计出版社, 2014: 5-24. [11] 苗金芳, 杨灿, 蒋光山. 基于新知识生产函数的青海高新技术企业创新驱动力研究[J]. 科技和产业, 2019, 19(12): 167-171. [12] 鲁晓东, 连玉君. 中国工业企业全要素生产率估计: 1999—2007[J]. 经济学(季刊), 2012, 11(2): 541-558. [13] 谢千里, 罗斯基, 张轶凡. 中国工业生产率的增长与收敛[J]. 经济学(季刊), 2008(3): 809-826. [14] 张杰, 李勇, 刘志彪. 出口与中国本土企业生产率——基于江苏制造业企业的实证分析[J]. 管理世界, 2008(11): 50-64. [15] CHEN X. Large sample sieve estimation of semi-nonparametric models [J]. Handbook of Econometrics, 2007, 6: 5549-5632.
[16] HOROWITZ J L. The bootstrap [J]. Handbook of Econometrics, 2001, 5: 3159-3228.
[17] 李玉红, 王皓, 郑玉歆. 企业演化: 中国工业生产率增长的重要途径[J]. 经济研究, 2008(6): 12-24. [18] BRANDT L, BIESEBROECK J V, ZHANG Y. Challenges of working with the Chinese NBS firm-level data [J]. China Economic Review, 2014, 30: 339-352.
[19] PELLEGRINO G, PIVA M. Innovation, industry and firm age: Are there new knowledge production functions? [J]. Eurasian Business Review, 2020, 10(1): 65-95.
[20] 戴觅, 余淼杰, MAITRA M. 中国出口企业生产率之谜: 加工贸易的作用[J]. 经济学(季刊), 2014, 13(2): 675-698. [21] 张杰, 李勇, 刘志彪. 出口促进中国企业生产率提高吗?——来自中国本土制造业企业的经验证据: 1999~2003[J]. 管理世界, 2009(12): 11-26. [22] 刘卉, 王永进. 代销出口与企业的生产率动态增长——基于动态结构模型的分析[J]. 经济科学, 2021(2): 47-58. [23] 李春顶. 中国出口企业是否存在“生产率悖论”: 基于中国制造业企业数据的检验[J]. 世界经济, 2010, 33(7): 64-81. [24] LU J, LU Y, TAO Z. Exporting behavior of foreign affiliates: Theory and evidence [J]. Journal of International Economics, 2010, 81(2): 197-205.
[25] DAI M, MAITRA M, YU M. Unexceptional exporter performance in China? The role of processing trade [J]. Journal of Development Economics, 2016, 121: 177-189.





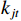












































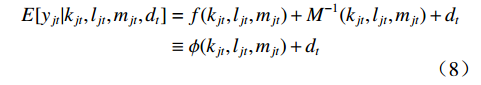




















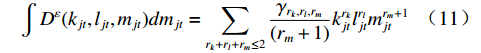










 下载:
下载:














