彗星或其他小行星的探测,尤其是不规则小行星的探测将成为未来深空探测中最为复杂的任务之一[1].针对探测器的下降和着陆控制,国内外学者做了许多研究工作.崔祜涛等人利用光学相机和激光雷达,提出自主制导方法,运用滑模变结构控制探测器着陆[2].以Apollo登月为背景,Li等人设计了燃料次最优多项式标称轨迹,提出了比例微分+脉宽脉频(PD+PWPF)控制方法[3].Broschart等人提出将探测器以自由下降的方式着陆在目标地点的控制方法,并详细地分析了控制跟踪误差[4].Zhang等人利用光学信息和卡尔曼滤波器,研究了自主导航算法,给出基于滑模变结构制导控制策略[5].Shao等人提出了一种利用三维散乱点方法对小天体表面进行三角剖分,建立了小行星多面体动力学模型[6].宋顺广等人运用蒙特卡罗法对月球着陆探测器进行了研究[7].为提高探测器着陆导航精度,高艾等人研究了一种对偶控制策略[8].Lan等人运用有限时间控制方法实现了探测器安全着陆小行星[9].邢健等人设计了自适应分层滑模控制器,抑制了燃料因素对航天器的扰动影响[10].
由于小行星具有不规则、分布不均等因素,设计合适的控制方法是完成探测任务的关键之处.PD控制方法具有响应快、易操作、系统稳定、克服对象惯性等特点,可以较好地实现动力下降段的控制要求;基于指数趋近律的非奇异Terminal滑模控制方法,避免了滑模面附近容易出现的奇异问题,提高了趋近滑模面的速度[11],减少了调整时间,保证了探测器在着陆段响应的快速性和稳定性. 1 探测器轨道动力学模型 1.1 小行星引力势能计算
小行星的不规则形状是导致其轨道动力学问题异常复杂的主要原因之一.文中采用球谐级数展开法表示小行星的引力势能,将目标小行星近似为三轴椭球体[12]:
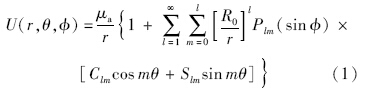
定义小行星固连坐标系Oaxayaza,原点在小行星质心,Oaza轴为小行星最大惯量轴,Oaxa轴为小行星最小惯量轴,Oaya轴由右手定则确定.定义探测器着陆点坐标系Olxlylzl,原点在着陆点,Olzl轴为小行星质心和着陆点连线的延长线,Olxl轴垂直于Olzl轴,Olyl轴由右手定则确定.θ和φ为着陆点的经度和纬度；R为小行星质心到探测器的位置矢量;r为着陆点到探测器的位置矢量.
建立固连坐标系下探测器轨道动力学方程[5]:
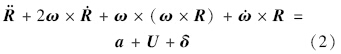
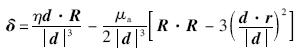
为求得着陆点坐标系下探测器的动力学方程,需将坐标系进行转换：
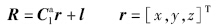
假设小行星以固定的角速度ωa绕z轴旋转,得到着陆点坐标系下探测器的动力学方程：
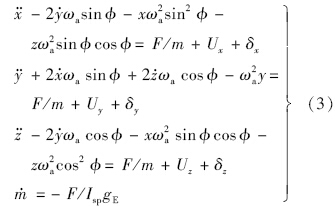
动力下降段是主推力制动发动机与小推力制动发动机同时工作的全推力制动过程,主要目的是减少探测器水平方向分量;当探测器飞行距离小行星几千米高度时进入着陆段,着陆段由小推力制动发动机工作半推力制动,调整探测器姿态,保证在最终几百米高度时进入垂直下降段[13].
软着陆是指探测器以相对于目标着落天体以较小的速度着陆,一般小于6m/s[14].依据燃料次最优制导理论,预先规划了探测器满足边界条件的轨迹方程[15]:
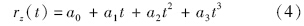
设定下降时间为τ,满足的边界条件:
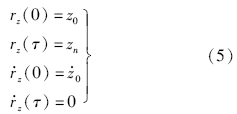
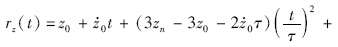
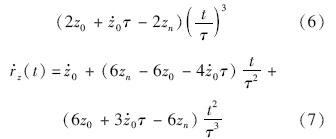
同样可以规划出x和y轴的位置和速度轨迹. 2.2 动力下降段和着陆段连续控制策略设计
定义探测器误差状态变量：
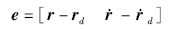
将探测器实际飞行轨迹与预先规划的标称轨迹作差,得出偏差值：
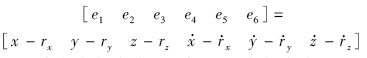
转换为状态方程,定义系统状态变量ei,ej(i=1,2,3;j=4,5,6),则
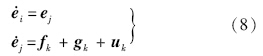
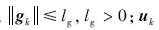表示控制量,(k=x,y,z).
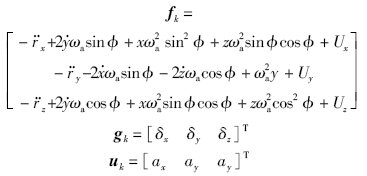
设计探测器动力下降段PD控制律:
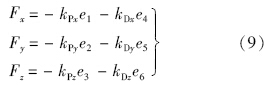
设计探测器着陆段时滑模面:
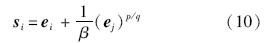
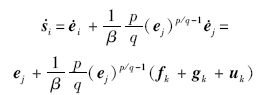
选取趋近律
=-εsgn(s)-ks,ε>0,k>0,是以i为元素的矩阵.令
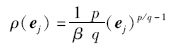
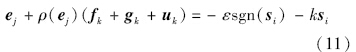
得到控制量uk:
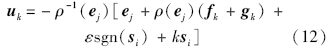
由于gk为系统的不确定项和扰动,可在控制量中对gk给系统的影响加以限制,同时为了避免控制量为0,在控制律中加入一个较小的常数ξ(ξ>0),得到新的控制量：
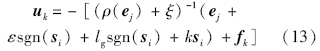
选择滑模面式(10),在控制量式(13)的作用下,可以保证系统在有限时间内到达滑模面,并使得跟踪误差在有限时间内收敛到0:
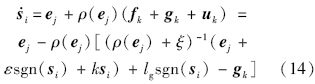
只要ξ足够小,可得ρ(ej)(ρ(ej)+ξ)-1=1,将式(14)简化得到
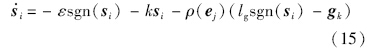
当ej≠0时,因为β>0,p/q∈(1,2),所以ρ(ej)>0,i≤-εsgn(si)-ksi<0.
在探测器接近小行星时可忽略gk的影响,可得i=-εsgn(si)-ksi,ej≠0.
当ej=0时,ρ(ej)=0,i=-εsgn(si)-ksi,ej.
考虑在控制量式(13)中含有(ρ(ej)+ξ)-1项,形式复杂、计算量大,为了提高探测器自主运算性能,将式(15)作进一步简化[17]:
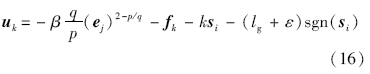
选择滑模面式(10),在控制量式(16)的作用下,可以保证系统在有限时间内到达滑模面,并使得跟踪误差在有限时间内收敛到0.
证明 对si求一次导数:
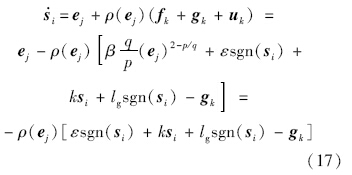
当ej=0时,ρ(ej)=0,i=-εsgn(si)-ksi,ej.
当ej≠0时,有ρ(ej)>0,可得si一次导数i≤-εsgn(si)-ksi<0.
选择Lyapunov函数:
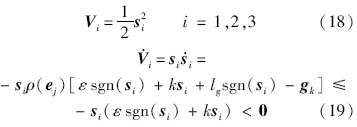
当且仅当si=0时,
i=0,控制器满足Lyapunov稳定条件,系统是鲁棒渐进稳定的.
在探测器着陆小行星时忽略gk的影响,则有
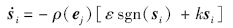
比较两种情况下,当ej≠0时,提出的趋近律相比于指数趋近律含有ρ(ej)项,称为伪指数趋近律(NTSM-PEAL);当ej=0时,趋近速度为指数形式.将非奇异Terminal指数趋近律(NTSM-EAL)和非奇异Terminal伪指数趋近律应用于不规则小行星控制系统中,可以保证Terminal滑模在非奇异的条件下,在较小控制作用下能够达到理想的控制效果. 3 仿真分析
以着陆某一颗小行星为例,对本文提出的控制方案的可行性进行仿真验证.对系统中存在的未建模不确定项,根据工程实际作出合理的假设,设δx=1.5sin2t,δy=1.6sin1.5t,δz=1.4sin3t,同时为了验证设计控制器的强鲁棒性,假设系统中的仿真参数存在着一定的误差值[3, 5].
设计Terminal滑模有关控制参数:β=2,p/q=1.5,k=2,lg=0.015.
图 1可看出探测器在动力下降段过程,下降轨迹平滑，表明控制器具有较强的鲁棒性和稳定性.图 2和图 3可看出在动力下降过程中,探测器在三轴运动位置均能渐近收敛,控制效果良好.
 |
| 图 1 动力下降段三维轨迹Fig. 1 Descending trajectory curve |
 |
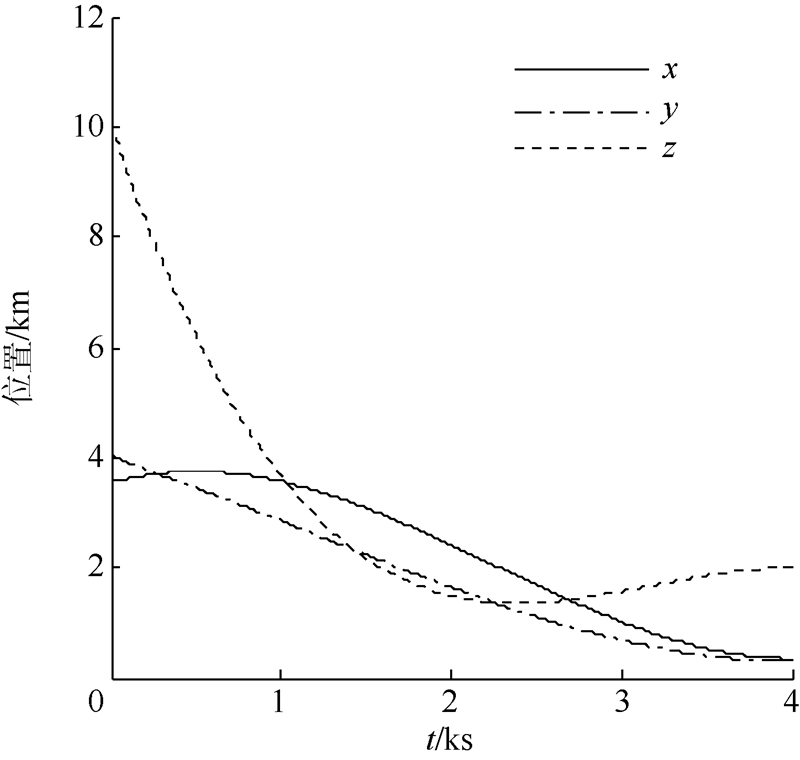| 图 2 动力下降段位置时间历程Fig. 2 Descending position time history |
 |
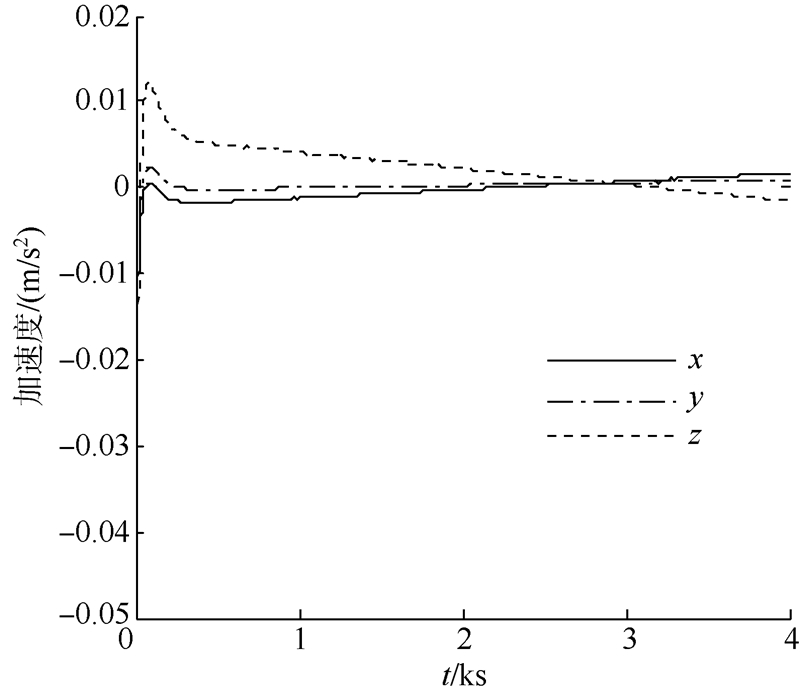| 图 3 动力下降段加速度时间历程Fig. 3 Descending acceleration time history |
图 4给出了探测器在普通滑模控制(SMC)和基于指数趋近律的非奇异Terminal滑模控制(NTSMC)下的着陆段三维轨迹.
 |
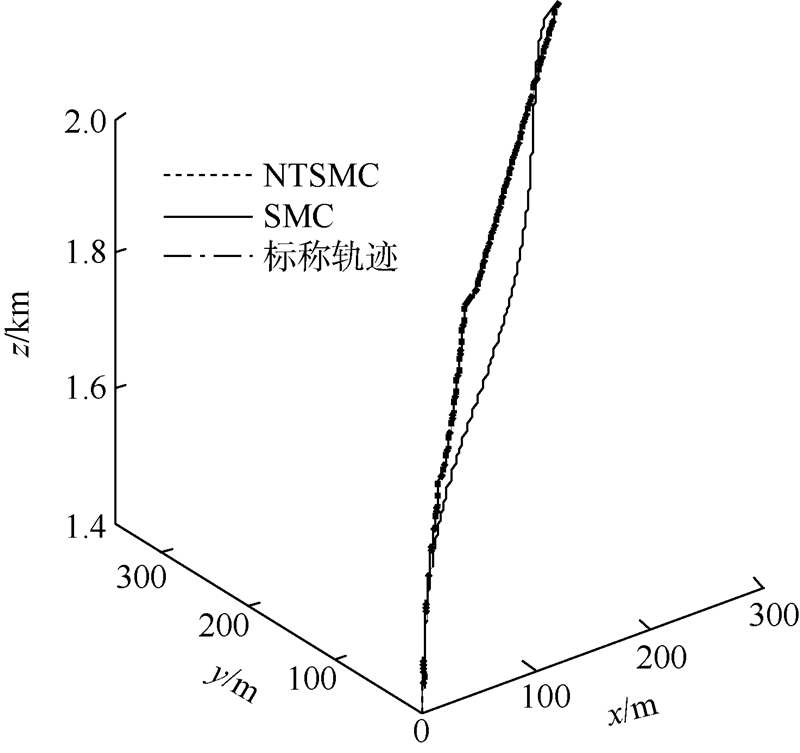| 图 4 着陆段三维轨迹Fig. 4 Landing trajectory curve |
图 5和图 6给出了在着陆段时探测器位置和控制加速度曲线.探测器在制动发动机的作用下,在x轴和y轴的位置和速度分量迅速收敛到0,只在z轴垂直方向存在控制力,实现探测器平稳垂直着陆.
 |
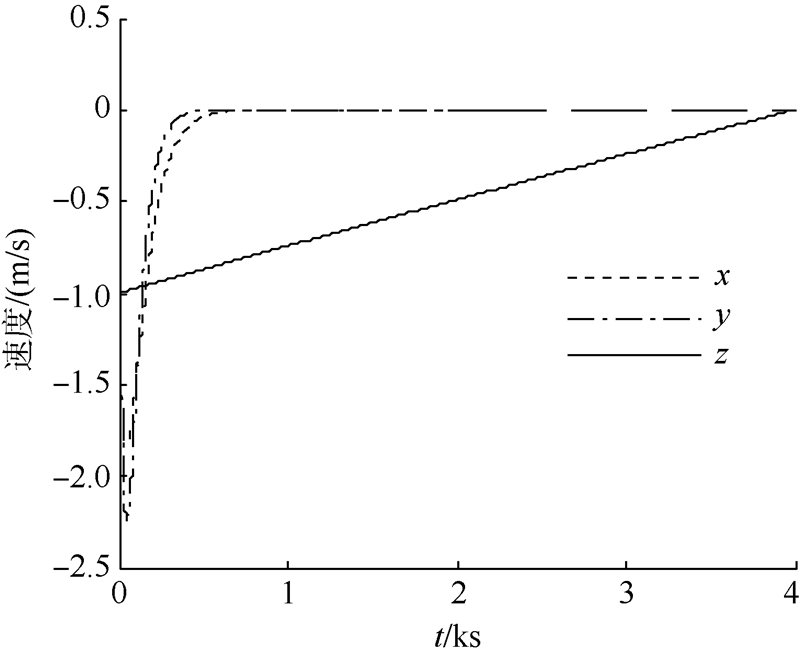| 图 5 着陆段位置时间历程Fig. 5 Landing position time history |
 |
| 图 6 着陆段加速度时间历程Fig. 6 Landing acceleration time history |
图 7给出了探测器在着陆段的质量变化曲线,随着制动发动机对燃料的消耗,探测器的质量不断减小,最终着陆时保持固定数值.由于控制系统具有较强鲁棒性,抑制了探测器质量变化对系统的扰动影响,探测器着陆过程平稳,满足工程实际要求.
 |
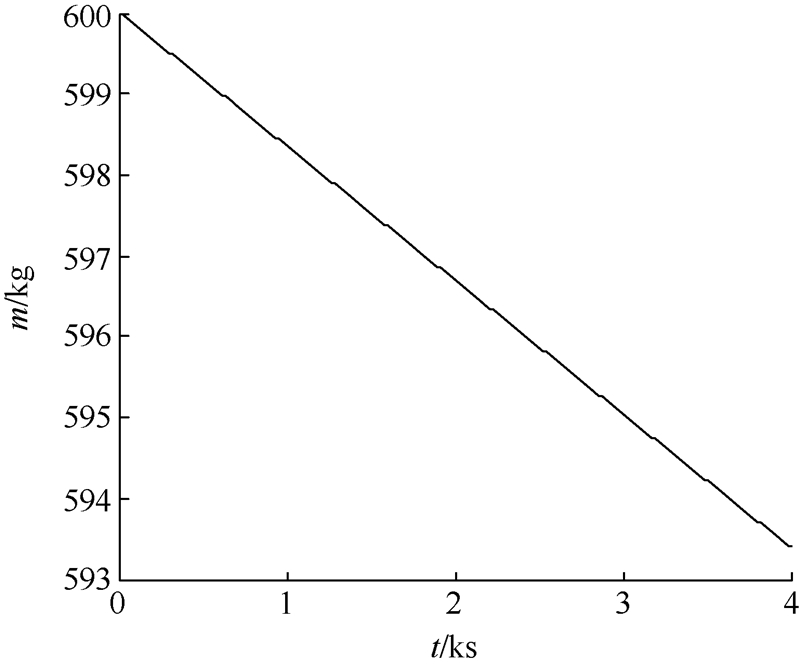| 图 7 探测器质量曲线Fig. 7 Mass curve of the probe |
图 4中将本文提出的基于指数趋近律的非奇异Terminal滑模控制方法与普通滑模控制方法相比,看出在基于指数趋近律的非奇异Terminal滑模控制下,探测器能够快速跟踪上预先规划的轨迹,并且保持较小误差的运动状态,系统的抖振和收敛时间小于普通滑模控制效果,减少了探测器在下降过程中的振荡,同时使得跟踪误差在有限时间内快速收敛到0,保证探测器最终安全着陆.实验结果表明文中提出的非奇异Terminal滑模控制方法比普通滑模控制效果更加安全、有效. 4 结 论
本文根据探测器在动力下降段和最终着陆段的不同飞行要求,提出了PD及非奇异Terminal滑模连续控制策略,很好地实现了不规则小行星探测器分时段控制.在动力下降段和最终着陆段基于燃料次最优的原则,规划了探测器飞行轨迹,仿真实验结果表明,所设计的PD控制器能够保证探测器平稳飞行接近小行星,基于指数趋近律的非奇异Terminal滑模控制器,在克服滑模面出现奇异问题的基础上,能够将探测器位置误差和速度误差快速收敛,较大程度地降低了探测器在着陆过程中的抖振,缩短了调整时间.探测器在着陆段将x和y轴方向的位置和速度分量迅速收敛到零,保证了探测器能够垂直处于预定着陆点上空,从而最终实现垂直软着陆.
| [1] | Sears D W G, Allen C C,Bell M S,et al.The hera near-earth asteroid sample return mission: science requirements of the sample collector[J].Advances in Space Research,2004,34(11): 22762280 |
| Click to display the text | |
| [2] | 崔祜涛, 崔平远.软着陆小行星的自主导航与制导[J].宇航学报,2002,23(5):1-5 Cui Hutao,Cui Pingyuan.Autonomous navigation and guidance for soft-landing asteroid[J].Journal of Astronautics,2002, 23(5): 1-5(in Chinese) |
| Cited By in Cnki (19) | |
| [3] | Li S,Cui P Y, Cui H T.Autonomous navigation and guidance for landing on asteroids[J].Aerospace Science and Technology,2006,10(3):239-247 |
| Click to display the text | |
| [4] | Broschart S B, Scheeres D J.Spacecraft descent and translation in the small-body fixed frame[R].AIAA-2004-4865,2004 |
| [5] | Zhang Z X, Wang W D,Li L T,et al.Robust sliding mode guidance and control for soft landing on small bodies[J].Journal of the Franklin Institute,2012,349(2):493-509 |
| Click to display the text | |
| [6] | Shao W, Cui P Y,Cui H T.Physical properties calculation of small body using points triangulations[J].Journal of Harbin Institute of Technology,2010,42(5):687-691 |
| Click to display the text | |
| [7] | 宋顺广,王春洁. 基于蒙特卡罗法的月球探测器着陆稳定性分析[J].北京航空航天大学学报,2013,39 (9):1192-1196 Song Shunguang,Wang Chunjie.Landing stability analysis of the lunar lander based on Monte Carlo approach[J].Journal of Beijing University of Aeronautics and Astronautics,2013,39(9):1192-1196(in Chinese) |
| Cited By in Cnki (1) | Click to display the text | |
| [8] | 高艾,崔平远, 崔祜涛.深空着陆器对偶控制策略[J].哈尔滨工业大学学报,2012,26(11):75-80 Gao Ai,Cui Pingyuan,Cui Hutao.Dual control strategy of planetary lander[J].Journal of Harbin Institute of Technology,2012,26(11):75-80(in Chinese) |
| Cited By in Cnki (2) | |
| [9] | Lan Q X, Li S,Yang J,et al.Finite-time control for soft landing on an asteroid based on line-of-sight angle[J].Journal of the Franklin Institute,2014,351(1):383-398 |
| Click to display the text | |
| [10] | 邢健,齐瑞云. 考虑燃料晃动效应的航天器自适应滑模姿态控制[J].空间控制技术与应用,2013,39(2):42-47 Xing Jian,Qi Ruiyun.Adaptive sliding-mode attitude control of spacecraft with fuel sloshing[J].Aerospace Control and Application,2013,39(2):42-47(in Chinese) |
| Cited By in Cnki | |
| [11] | 曾宪法, 王小虎,张晶,等.高超声速飞行器的干扰补偿 Terminal 滑模控制[J].北京航空航天大学学报,2012, 38(11): 1454-1458 Zeng Xianfa,Wang Xiaohu,Zhang Jing,et al.Disturbance compensated terminal sliding mode control for hypersonic vehicles[J].Journal of Beijing University of Aeronautics and Astronautics,2012,38(11):1454-1458(in Chinese) |
| Cited By in Cnki (2) | Click to display the text | |
| [12] | Washabaugh P D, Scheeres D J.Energy and stress distributions in ellipsoids[J].Icarus,2002,159(2):314-321 |
| Click to display the text | |
| [13] | 单永正. 月球探测器软着陆的制导问题研究[D].哈尔滨:哈尔滨工业大学,2009 Shan Yongzheng.Research on guidance problem of lunar probe for soft landing[D].Harbin:Harbin Institute of Technology,2009(in Chinese) |
| Cited By in Cnki (5) | |
| [14] | 郗晓宁,曾国强, 任萱,等.月球探测器轨道设计[M].北京:国防工业出版社,2001:119-139 Xi Xiaoning,Zeng Guoqiang,Ren Xuan,et al.Lunar probe track design[M].Beijing:National Defense University Press,2001:119-139(in Chinese) |
| [15] | 孙军伟,崔平远. 月球软着陆多项式制导控制方法[J].宇航学报,2007,28(5):1171-1174 Sun Junwei,Cui Pingyuan.Polynomial guidance law for lunar soft landing[J].Journal of Astronautics,2007,28(5):1171-1174(in Chinese) |
| Cited By in Cnki (7) | |
| [16] | Feng Y, Yu X H,Man Z H.Non-singular terminal sliding mode control of rigid manipulators[J].Automatica,2002,38(12):2159-2167 |
| Click to display the text | |
| [17] | 张巍巍, 王京.基于指数趋近律的非奇异Terminal滑模控制[J].控制与决策,2012,27(6):909-913 Zhang Weiwei,Wang Jing.Nonsingular terminal sliding model control based on exponential reaching law[J].Control and Decision,2012,27(6):909-913(in Chinese) |
| Cited By in Cnki (6) |
