飞行品质监控(FOQA,Flight Operations Quality Assurance)是促进民航业持续安全的一项基础性工作,具有事先预防航空事故的重要功效.FOQA利用机载QAR(Quick Access Recorder)记录的飞行数据,依据事先设定的监控项目和标准从中发现各种超限事件.目前我国民航FOQA工作方式存在如下明显不足:①监控标准主要依据单一飞行参数以“[下限,上限]”形式确定,以这种方式进行超限事件检测很容易由于数据噪声而导致误判,实际上在某一超限事件发生时,可能会有若干个QAR参数与之相关联,如果能综合运用多个QAR参数进行超限事件诊断,便可以有效减少如上问题的发生;②QAR数据利用率低,没有对其进行深入挖掘分析,查找其蕴含的安全规律.
针对如何开展QAR数据深度分析以提高飞行安全,国内外学者开展了一些研究工作.美国国家航空航天局(NASA)的AMES研究中心提出了一系列进行飞行品质异常检测的方法.这些方法包括基于K-近邻的Orca[1]、基于聚类的IMS[2]和SequenceMiner[3]、基于核函数的MKAD[4].Smart等人[5]基于支持向量机(SVM,Support Vector Machine)进行了飞行品质异常检测研究,该方法分为2个阶段:第1阶段检测某个航班在降落阶段各个高度的异常;第2阶段根据第1阶段SVM的输出比较航班之间的异常,从而发现最异常的航班,还应用特征选择F-score技术寻找与飞行异常相关的关键飞行参数.在国内,黄圣国等人[6,7]基于SVM构建了民用飞机的重着陆智能诊断模型,曹海鹏等人[8]基于神经网络对民用飞机重着陆事件做了研究.这些方法均通过物理机理分析获得与重着陆相关的飞行参数,然后从QAR数据集中截取数据构成训练样本进行建模.祁明亮等人[9]利用优选法和数理统计法,选取飞机下降率、俯仰角等飞行员综合操作指标,确定可能触发某一超限事件的高风险区域.上述与本文相关的基于SVM和神经网络的方法都属“黑盒”建模法,这些方法虽然能够识别超限事件,但是不能较好地解释超限事件发生的原因,即模型的解释性较差.
模糊关联分类器(FAC,Fuzzy Associative Classifier)是数据挖掘研究领域重要的分类方法之一[10,11,12],是在高维数据集上构建模糊分类器的一种有效方法[13],其最大特点在于完全从数据出发,发现有趣的关联,挖掘数据集中的多个变量与样本类别之间的规律性,以其较高的分类精度和较好的解释性受到了研究关注.为此,本文采用Apriori算法和遗传算法构建了基于模糊关联分类器的超限事件诊断模型,该模型扩展了超限事件的判定指标,实现了多因素的超限事件诊断,真实QAR数据集上的实验表明了本文方法的有效性.
1 模糊关联分类器的相关定义
设有数据集D=[X y]N×(n+1),其中X=[xk,l]N×n为在数量属性z1,z2,…,zn上的N个取值,y=[yk]N×1为在类别属性zn+1上的取值,D中第k(1≤k≤N)个样本xk在数量属性zi(1≤i≤n)上的模糊隶属度值表示为:uk,i=[Ai,1(xk,i),Ai,2(xk,i),…,Ai,qi(xk,i)],其中Ai,1,Ai,2,…,Ai,qi为数量属性zi对应的隶属度函数,qi为属性zi的隶属度函数的个数.数据集D可由各个数量属性上的隶属度函数转化为取值在[0,1]之间的模糊数据集Df={t1,t2,…,tN},其中tk=[uk,1,uk,2,…,uk,n,yk](1≤k≤N).定义〈zi∶Ai,j〉为模糊项,模糊项集定义为
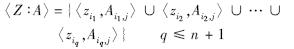
定义1 模糊项集〈Z∶A〉的支持度定义为
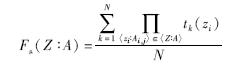
若Fs(〈Z∶A〉)大于指定的最小支持度,则称〈Z∶A〉为模糊频繁项集.其中tk(zi)为第k个数据在属性zi对应的隶属度函数Ai,j上的取值;∏表示乘法运算.
定义2 若模糊关联规则〈Z∶A〉 〈y∶C〉的后件只含类别属性,则称为模糊关联分类规则(FACR,Fuzzy Associative Classification Rule),其置信度定义为
〈y∶C〉的后件只含类别属性,则称为模糊关联分类规则(FACR,Fuzzy Associative Classification Rule),其置信度定义为
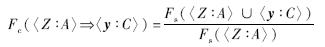
定义3 模糊关联分类规则的模糊相关度定义为
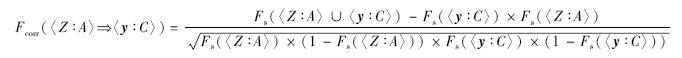
Fcorr取值范围为[-1,1],规则的模糊相关度越接近1,模糊关联分类规则的质量越高.
定义4 模糊关联分类器的解释性:文中以分类器包含的FACR数目与FACR前件中包含的模糊项总数为衡量指标,FACR数目和总的模糊项数目越少,模糊关联分类器的解释性越好.
2 基于模糊关联分类器的超限事件诊断建模
基于模糊关联分类器的超限事件诊断建模流程如图 1所示.首先从经译码、格式化后的QAR数据中,抽取发生超限事件时与飞行品质相关的QAR参数快照取值构成训练和测试数据集,采用模糊C均值(FCM,Fuzzy C-Means)聚类算法对数据集模糊预处理.然后基于Apriori算法生成模糊频繁项集,由模糊频繁项生成模糊相关度大于0的FACR构成分类规则库.为使模糊关联分类器具有较好的解释性,最后基于遗传算法裁剪FACR规则库,裁剪后的分类规则库结合模糊分类推理引擎形成超限事件诊断模型.
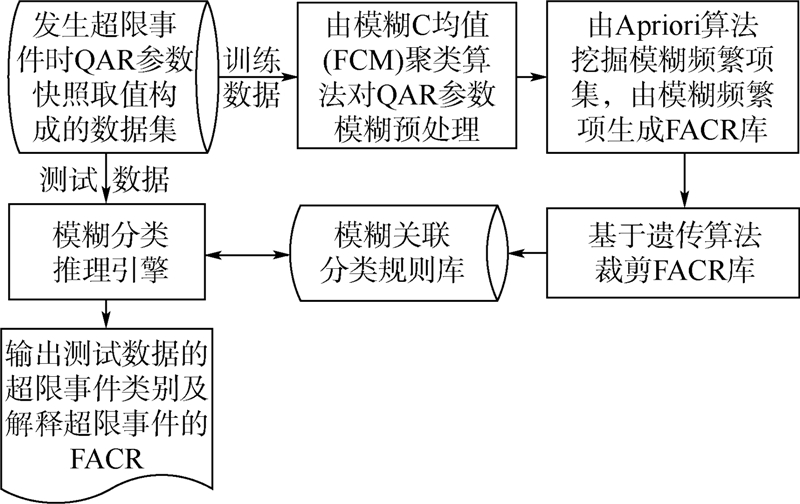 |
| 图 1 基于模糊关联分类器的超限事件诊断建模流程图Fig. 1 Flow chart of building exceedance event diagnosis model based on fuzzy associative classifier |
挖掘模糊频繁项以及生成FACR的具体算法描述如下.
输入:经模糊预处理后的数据集Df,最小模糊支持度计数msup;
输出:Df中的所有模糊频繁项集L;
扫描Df生成1-模糊频繁项集,记为L1;
For (k=2;Lk≠Ø;k++) doCk=apriori-Gen(Lk-1);/*由(k-1)-模糊频繁项集生成候选模糊项集Ck*/
For each t∈Df do/*扫描Df,求Ck中模糊项集的支持度计数*/
Ct=subset(Ck,t);/*求事务t所能包含Ck中的模糊项集*/
For each模糊项c∈Ct do
ccount=ccount+T(u1t,u2t,…,ukt);
/*计算模糊项c的支持度计数ccount,T为t-模算子,文中取乘法运算,uit表示c中的第i(1≤i≤k)项在事务t上的取值;*/
End for
End for
Lk={c∈Ckccount≥msup}
End for所有模糊频繁项集L=L1∪L2∪…∪Lk;
上述算法中由(k-1)-模糊频繁项集生成候选模糊项集Ck的apriori-Gen(Lk-1)具体步骤如下:
For each模糊项l1∈Lk-1For each模糊项l2∈Lk-1
If (l1[1]=l2[1])∧(l1[2]=l2[2])∧…∧(l1[k-2]=l2[k-2])∧l1[k-1]与l2[k-1]为两个不同数量性对应的模糊项Then
由l1,l2生成新的模糊项 c=l1[1]l2[2]…l1[k-2]l1[k-1]l2[k-1];
If c的每个包含k-1模糊项的子集s都属于Lk-1 Then
新生成的模糊项c加入Ck;
End ifEnd if
End for
End for ProcMineFuzzyClassifyRule (L) /*算法的输入为除1-模糊频繁项的模糊频繁项集L*/ For each l∈LFor each l′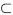 l
l
If l-l′中只含类别属性并且
Fcorr(l′ l-l′)>0 then
l-l′)>0 then
R=R∪(l′ l-l′);/*集合R为初始模糊关联分类规则集*/
l-l′);/*集合R为初始模糊关联分类规则集*/
End if
End for
End for2.1 基于遗传算法的模糊关联分类规则库裁剪方法
遗传进化种群的个体采用二进制编码方式,设初始分类规则库有M个FACR,则群体中的每个个体可表示为长度M的二进制串:s1s2…sM,每个si(1≤i≤M)取值0或1.0表示该基因位对应的FACR不在构成FAC的规则库中,1则表示对应的FACR包含在FAC的规则库中.种群个体间的交叉方式采用HUX(Half Uniform Crossover)交叉算子,为尽量减少FAC中分类规则的数量,采用有偏向的变异算子,即个体中的每个基因位由0至1的变异概率高于1至0的变异概率,交叉和变异算子的具体描述见文献[14].模糊关联分类器的准确率和解释性是两个相互制约的优化目标,文中进化群体中个体S的适应度函数设计如式(1):

2.2 模糊分类推理方法
图 1中的模糊分类推理引擎使用的分类推理方法描述如下[15]:设由遗传算法裁剪后的模糊关联分类规则库由R条规则组成,待分类的样本xk对分类模型中的第j条规则的激励强度按式(2)计算:
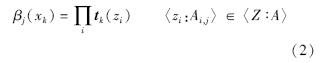
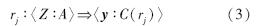
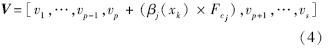
由式(4)可知积分向量V中第p个分量值增加了样本xk对第j条规则的激励度βj(xk)与规则置信度Fcj的乘积,按此方法,对于分类规则库中的所有规则,积分向量V中的每个分量值可按式(5)计算:
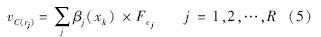
待分类样本xk的类别为积分向量V中积分值最大的分量对应的类别,即yk=argmax(V).
3 实际应用及结果分析
实验数据来自某航空公司B737-800的机载QAR数据集,从中抽取发生“50ft至接地距离长”和“拉平着陆坡度大”两类三级超限事件时各200个航班对应的QAR参数快照取值.根据领域工程师经验知识,取与所选超限事件相关的15个QAR参数,对每个参数取值采用Matlab中的FCM聚类算法模糊预处理,聚类数目均为3,隶属度矩阵的加权指数m取值为2,对应为低、中、高3个模糊项.选取的15个参数及其取值范围、聚类中心描述如表 1所示.
| 参数 | 取值范围 | 聚类中心 | ||
| 低 | 中 | 高 | ||
| 磁航向/(°) | [0, 363] | 34.47 | 194.19 | 333.15 |
| 仰角/(°) | [-2.1,5.3] | 0.59 | 2.37 | 4.01 |
| 坡度/(°) | [-9.6,7.7] | -5.09 | -0.26 | 5.12 |
| 大气总温/℃ | [-11,34] | 2.33 | 13.12 | 23.59 |
| N1/(%r/min) | [26,68.9] | 31.30 | 43.63 | 57.29 |
| 全重/lb | [55280, 143920] | 60345 | 112000 | 133000 |
| 方向舵位置/(°) | [-10,10.6] | -5.42 | -1.01 | 1.88 |
| 地速/kn | [101, 169] | 119.83 | 135.52 | 148.72 |
| 左副翼位置/(°) | [-10.9,13.8] | -4.40 | 2.18 | 7.79 |
| 右副翼位置/(°) | [-12.5,11.1] | -5.93 | 0.77 | 6.58 |
| 左升降舵位置/(°) | [-9.5,6.2] | -5.40 | -2.40 | 1.97 |
| 右升降舵位置/(°) | [-9.5,6] | -5.31 | -2.37 | 1.91 |
| 风速/kn | [0, 41] | 4.62 | 15.40 | 28.94 |
| 风向/(°) | [-176.8,345.8] | -134.08 | 0.98 | 137.71 |
| 压力高度/ft | [-576,6844] | 63.28 | 2045.70 | 6509.20 |
| 注:1lb=0.45359237kg; 1ft=0.3048 m. | ||||
将400组数据采用分层抽样的方法随机划分为3个部分,其中2部分作为训练集,剩余部分作为测试集.裁剪模糊关联分类规则库的遗传算法参数设置如表 2所示.实验环境为WinXP,CPU 2.93GHz,2.0GB内存,Visual C++6.0.
| 参数 | 数值 |
| 进化种群大小 | 200 |
| 进化迭代次数 | 100 |
| 交叉概率 | 0.9 |
| 变异概率(1→0) | 0.1 |
| 变异概率(0→1) | 0.001 |
表 3列出了本文的FAC在不同最小支持度取值下生成的初始分类规则数目、经遗传算法裁剪后分类规则库中规则数目及所有规则前件中包含的模糊项总数及其对应的分类模型在训练集和测试集上的分类错误率.从表 3中可以看出随着最小支持度的增大,FAC在训练集上的分类错误率整体上呈下降趋势.这是因为最小支持度的增大使得初始分类规则集中的规则质量提高,而且分类规则数目变少,缩小了遗传算法的搜索空间,有利于筛选较好的分类规则.但从表 3中也发现最小支持度为0.10和0.15时,生成的FAC在测试集上的分类错误率还低于在训练集上的分类错误率,这可能是因为最小支持度为0.10和0.15时,经裁剪后分类规则库中包含的分类规则数目相对较多,分类推理能力较强,而测试集中的样本数目相对训练集较少,从而造成测试集上的分类错误率低于训练集.
| 最小支持度 | 初始规则数 | 裁剪后的规则数及模糊项总数 | 分类错误率 | |
| 训练集 | 测试集 | |||
| 0.10 | 3077 | 674,2677 | 0.08 | 0.07 |
| 0.15 | 943 | 96,312 | 0.03 | 0.02 |
| 0.20 | 319 | 11,22 | 0.04 | 0.05 |
| 0.25 | 137 | 4,5 | 0.04 | 0.07 |
| 0.30 | 74 | 3,3 | 0.01 | 0.04 |
| 0.35 | 39 | 2,2 | 0.01 | 0.01 |
限于篇幅,表 4只列出了最小支持度0.25与0.30对应的FAC分类规则库中的规则及每条规则的置信度.可以看出,模糊项坡度高、风速中与超限事件“拉平着陆坡度大”关联性较大,而坡度中、风速低与超限事件“50ft至接地距离长”关联性较大.
| 最小支持度 | 模糊关联分类规则 | 置信度 |
| 0.25 | 坡度高→拉平着陆坡度大 | 0.98 |
| 方向舵位置中→拉平着陆坡度大 | 0.53 | |
| 风速中→拉平着陆坡度大 | 0.88 | |
| 坡度中,风速低→50ft至接地距离长 | 0.99 | |
| 0.30 | 坡度中→50ft至接地距离长 | 0.97 |
| 风速中→拉平着陆坡度大 | 0.88 | |
| 压力高度低→拉平着陆坡度大 | 0.53 |
图 2为最小支持度取值为0.20,0.25,0.30,0.35时,基于遗传算法裁剪模糊关联分类规则库过程中适应度函数取值的变化趋势图.从图 2中不难发现:随着迭代次数的增加,上述4个最小支持度取值对应的适应度取值逐步增大,最后均能收敛于某个值.而且最小支持度值越大,遗传适应度函数的收敛值越大.根据文中2.1节设计的适应度函数分析可知,最小支持度取值较大时,FAC在训练集中正确分类的样本数目多,分类规则库中包含规则数目和模糊项数目总和较少,这与表 3中的实验结果一致.
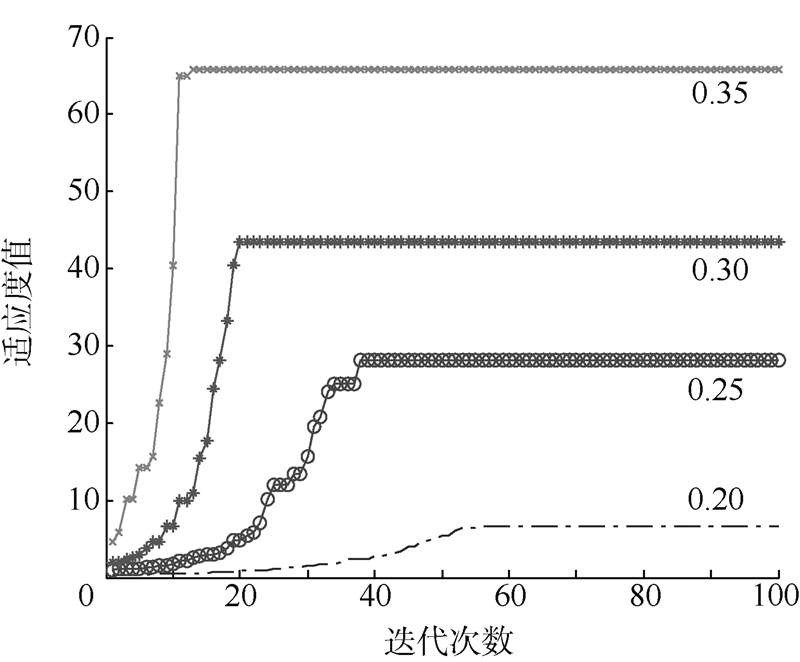 |
| 图 2 不同的最小支持度对应的适应度值变化图Fig. 2 Changing trend of fitness value corresponding to different minimum support threshold |
本文比较了LS-SVM与文中FAC在所选取的QAR数据集上的分类性能.实验采用美国北卡罗莱纳那州立大学开发的基于LS-SVMlab1.8软件的Matlab工具箱,选取常用的径向基(RBF)函数作为LS-SVM的核函数对模型进行训练.实验过程中首先在选取的400组数据上,基于3-折交叉验证,分别采用单纯形法、网格搜索法对LS-SVM的参数gam和sig2进行优化,然后采用与上文训练模糊关联分类器相同的样本划分方法训练LS-SVM分类模型.表 5列出了两种参数优化方法对应的gam和sig2取值及由其所训练的LS-SVM分类模型在测试集上的分类错误率.结合表 3的结果对比分析,最小支持度为0.30时,FAC在测试集上的分类错误率为0.04,与表 5中单纯形法对应的LS-SVM分类错误率相同;最小支持度0.35时,FAC在测试集上的分类错误率为0.01,低于表 5中网格搜索法对应的LS-SVM分类错误率0.02.而且本文FAC在解释性方面也优于LS-SVM.
| 参数优化法 | gam | sig2 | 分类错误率 |
| 单纯形法 | 52971 | 8.12 | 0.04 |
| 网格搜索法 | 201.97 | 5.06 | 0.02 |
1) 建立的基于模糊关联分类器的民用飞机超限事件诊断模型能较好地识别超限事件,模型中包含的模糊关联分类规则有助于实现多因素的超限事件诊断.
2) 与目前用于民机超限事件诊断的LS-SVM模型相比,本文模型在所采用B737-800的数据集上分类准确率相当,对领域工程师分析超限事件发生的原因具有辅助作用.
3) 本文的民用飞机超限事件建模方法完全基于数据驱动,与实际基于监控标准阈值判定超限事件的方法相比,提高了QAR数据的利用率.下一步可把领域工程师的经验知识融入模型,进一步提高该诊断模型的可用性.
| [1] | Bay S D, Schwabacher M.Mining distance-based outliers in near linear time with randomization and a simple pruning rule[C]//Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York:ACM,2003:29-38 |
| [2] | Iverson D L. Inductive system health monitoring[C]//Proceedings of the International Conference on Artificial Intelligence,IC-AI'04.Las Vegas:CSREA Press,2004:605-611 |
| [3] | Budalakoti S, Srivastava A N,Otey M E.Anomaly detection and diagnosis algorithms for discrete symbol sequences with applications to airline safety[J].IEEE Transactions on Systems,Man,and Cybernetics,Part C:Applications and Reviews,2009, 39(1): 101-113 |
| Click to display the text | |
| [4] | Das S,Matthews B L, Srivastava A N,et al.Multiple kernel learning for heterogeneous anomaly detection:algorithm and aviation safety case study[C]//16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,KDD-2010.New York:ACM,2010:47-56 |
| Click to display the text | |
| [5] | Smart E, Brown D,Denman J.Combining multiple classifiers to quantitatively rank the impact of abnormalities in flight data[J].Applied Soft Computing,2012,12(8):2583-2592 |
| Click to display the text | |
| [6] | 聂磊,黄圣国,舒平,等. 基于支持向量机的民用飞机重着陆智能诊断研究[J].中国安全科学学报,2009,19(7):149-153 Nie Lei,Huang Shengguo,Shu Ping,et al.Intelligent diagnosis for hard landing of aircraft based on SVM[J].China Safety Science Journal,2009,19(7):149-153(in Chinese) |
| Cited By in Cnki (3) | |
| [7] | 许桂梅,黄圣国. 基于优化支持向量机的飞机重着陆智能诊断[J].计算机测量与控制,2011,19(2):256-259 Xu Guimei,Huang Shengguo.Airplane' s hard landing diagnosis based on optimized support vector machine[J].Computer Measurement & Control,2011,19(2):256-259(in Chinese) |
| Cited By in Cnki (3) | |
| [8] | 曹海鹏,舒平, 黄圣国.基于神经网络的民用飞机重着陆诊断技术研究[J].计算机测量与控制,2008,16(7):906-908 Cao Haipeng,Shu Ping,Huang Shengguo.Study of aircraft hard landing diagnosis based on neural network[J].Computer Measurement & Control,2008,16(7):906-908(in Chinese) |
| Cited By in Cnki (11) | |
| [9] | 祁明亮,邵雪焱, 池宏.QAR超限事件飞行操作风险诊断方法[J].北京航空航天大学学报,2011,37(10):1207-1210 Qi Mingliang,Shao Xueyan,Chi Hong.Flight operations risk diagnosis method on quick access record exceedance[J].Journal of Beijing University of Aeronautics and Astronautics,2011, 37(10): 1207-1210(in Chinese) |
| Cited By in Cnki (3) | |
| [10] | 董杰,韩敏. 基于自适应区间划分的模糊关联分类[J].系统仿真学报,2009,21(9):2675-2678 Dong Jie,Han Min.Fuzzy associative classification based on adaptive interval partition[J].Journal of System Simulation,2009,21(9):2675-2678(in Chinese) |
| Cited By in Cnki (1) | |
| [11] | 董杰,沈国杰. 一种基于模糊关联分类的遥感图像分类方法[J].计算机研究与发展,2012,49(7):1500-1506 Dong Jie,Shen Guojie.Remote sensing image classification based on fuzzy associative classification[J].Journal of Computer Research and Development,2012,49(7):1500-1506(in Chinese) |
| Cited By in Cnki | |
| [12] | 霍纬纲,邵秀丽. 一种基于多目标进化算法的模糊关联分类方法[J].计算机研究与发展,2011,48(4):567-575 Huo Weigang,Shao Xiuli.A fuzzy associative classification method based on multi-objective evolutionary algorithm[J].Journal of Computer Research and Development,2011,48(4):567-575(in Chinese) |
| Cited By in Cnki (6) | |
| [13] | Alcalá-Fdez J, Alcalá R,Herrera F.A fuzzy association rule-based classification model for high-dimensional problems with genetic rule selection and lateral tuning[J].IEEE Transactions on Fuzzy Systems,2011,19(5):857-872 |
| Click to display the text | |
| [14] | 霍纬纲,高小霞. 一种适用于多类不平衡数据集的模糊关联分类方法[J].控制与决策,2012,27(12):1833-1838 Huo Weigang,Gao Xiaoxia.A fuzzy associative classification method for multi-class imbalanced dataset[J].Control & Decision,2012,27(12):1833-1838(in Chinese) |
| Cited By in Cnki | |
| [15] | Pach F P, Gyenesei A,Abonyi J.Compact fuzzy association rule-based classifier[J].Expert Systems with Application,2008, 34(4): 2406-2416 |
| Click to display the text |


