Download PDF  
文章快速检索  
  高级检索
引用本文
杨宇翔, 张汇川. 同步三星目标运动状态快速检测方法[J]. 北京航空航天大学学报, 2014, 40(10): 1392-1398
Yang Yuxiang, Zhang Huichuan. Fast algorithm of motion state detection based on tri geo-satellites[J]. Journal of Beijing University of Aeronautics and Astronsutics, 2014, 40(10): 1392-1398.
同步三星目标运动状态快速检测方法
杨宇翔, 张汇川    
西南电子电信技术研究所, 成都 610041
收稿日期:2013-11-5; 网络出版日期: 2014-03-13
基金项目：国家高技术研究发展计划(863计划)资助项目(2012AA7074012).
作者简介: 杨宇翔(1984-),男,重庆人,博士生,yyxforever@163.com.
摘要：针对星载无源定位系统难以从定位结果及时准确地检测目标运动状态的问题,利用同步三星时差定位体制的定位误差特性,根据静止假设下同步双星时/频差与三星定位结果应相匹配的原理,提出了基于定位一致性的目标运动状态快速检测算法.先通过定位结果的误差分析掌握目标实际位置所在区域,然后在静止假设下统计该区域的频差范围,并将定位时刻的频差观测值与之比较,实现目标运动状态检测,并且推导了检测概率的理论表达式.仿真和试验结果验证了算法的有效性,时/频差估计误差标准差为10 μs/100 mHz时,对速度大于40 m/s的目标,检测概率高于99%.实测数据表明该算法显著提高了系统目标运动状态检测的准确性和时效性.
关键词： 频差     时差     无源定位     误差椭圆     运动状态检测    
Fast algorithm of motion state detection based on tri geo-satellites
Yang Yuxiang, Zhang Huichuan     
Southwest Electronics and Telecommunication Technology Research Institute, Chengdu 610041, China
Abstract:Aiming at the difficulty to detect the motion state of targets in the satellite-borne passive location system, a fast motion state detection algorithm, based on the principle that the location result of the dual-satellites geolocation using differential time offset (DTO) and differential frequency offset (DFO) should be consistent with that of the tri-satellites geolocation using dual DTOs under the stationary hypothesis, was proposed. Firstly the region of target was obtained by location error analysis. Then the DFO range of this region under the stationary hypothesis was obtained through the statistics. Finally the observed value of DFO at the location time was compared with the DFO range to detect the motion state of target. And the expression of theoretical detection probability was given. The algorithm was verified by the simulation and experiment results. For the targets with velocity above 40 m/s, the detection probabilities are more than 99% when the estimation precision of DTO/DFO is 10 μs/100 mHz. It is demonstrated by the practical data that the proposed algorithm helps the system improve the ability to detect motion state significantly.
Key words: differential frequency offset (DFO)     differential time offset (DTO)     passive location     error ellipse     motion state detection    

基于同步卫星的星载无源定位系统[1,2],利用空间同步卫星作为接收平台,采用无源定位体制[3,4,5,6],能实现静止或运动目标辐射源定位.获取目标位置是其主要任务,但在实际应用中,往往还期望能准确地检测定位目标的运动状态,以区分静止和运动目标:对静止目标可多次观测定位并融合处理,获取精度更高的位置信息;对移动目标则需给予重点关注,及时掌握其动态.

但是,受限于参数测量精度、卫星星历精度和定位几何等原因,星载无源定位的误差较大,同时目标移动引起的位置变化相比同步卫星高度很小,不能及时反映到定位结果中,导致移动和静止目标的定位结果具有类似的分布特性,只有长时间连续定位观测,两者的差异才会显现.然而,目标信号的持续时间往往较短,无法提供足够的定位点用于判断.因此,目标运动状态检测的准确性和时效性都有待提高.

文献[7]认为目标移动必然引起方位角变化,提出基于蚁群聚类的静止目标检测方法,将大量定位结果以方位角进行聚类.归入同类的则为静止目标,分散在不同方位角类别的则是移动目标.但它需要大量定位结果作为样本进行学习进化,并且对本文而言,目标距离卫星太远,移动带来的方位角变化很小,而基于同步卫星无法获得高精度的方位角信息,该方法并不适用.文献[8]针对移动目标的检测问题,提出了广义最大似然比方法,在静止和运动两种假设下通过非线性观测方程对目标的位置和速度估计,并结合参数测量结果计算似然比,最终与门限比较完成检测.但其将目标运动模型严格约束为地面匀速运动,意图通过遍历搜索的方式找出与多组参数测量结果最匹配的目标位置和速度,运算量大,局限性强,并且存在严重的多值解问题[9],难以实现.文献[10]在文献[8]的基础上进行了改善,通过观测方程的线性化处理和新判决准则的选择,避免了运动假设下目标位置和速度的联合估计,提出了拟合度检验和Rao检测方法,大幅降低了算法复杂度,仅需通过静止假设下的目标位置最大似然估计获得检验统计量.但它仍然需要多次测量和足够的观测时间支撑,时效性较差,且由于参数测量精度与星历误差、转发器延迟等诸多因素有关,其误差协方差矩阵将随时间变化,影响目标位置最大似然估计结果的准确性,检测概率不高.

星载平台自身存在运动的特点,使其能在双星组合下,对静止目标定位[11].根据静止假设下双星时/频差和三星双时差定位结果应相匹配的原理,提出了基于定位一致性的目标运动状态快速检测算法,并推导了检测概率的理论表达式.仿真和试验结果表明检测概率统计值与理论值相符,一次测量即可完成检测,在时/频差估计误差标准差10 μs/100 mHz时,对速度大于40 m/s的目标,检测概率高于99%,有效解决了星载无源定位系统中目标运动状态的检测问题. 1 组成及原理

空间3颗同步卫星,分别接收到目标信号,并透明转发至地面接收站,如图 1所示.其中,引入位置已知的参考站,是为了消除和减少传播路径引起的相位噪声、卫星转发器延迟、设备不理想等产生的误差,提高定位的精度.

图 1 定位系统示意图 Fig. 1 Schematic diagram of location system
图选项
1.1 同步三星时差定位原理

由于传播路径距离的不同,信号到达3颗同步卫星的时间也不相同.利用卫星S1和S2间的时差DTO1形成双曲面与地球表面相交,得到一条时差线,同理卫星S1和S3之间的时差DTO2也构成一条时差线,两条时差线交点即为目标位置.

在地固坐标系中,假设卫星位置分别为rS1,rS2和rS3,目标位置为r,参考站位置r0,则时差方程为

其中,τ1(r)和τ2(r)表示目标的DTO;c为光速.

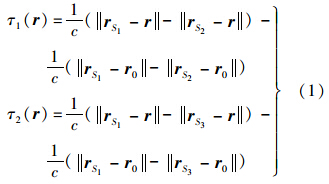
将其联立地球方程,如式(2)所示,便可完成目标位置解算.

其中,a为地球椭球模型长半轴;b为短半轴.

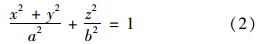
由于方程未涉及目标速度信息,无论目标静止或移动,均能定位. 1.2 同步双星时/频差定位原理

如图 1所示,三星组合中包含两组不冗余的双星组合,结合目标与卫星间径向速度不同引起的频差信息,利用时/频差定位技术[11],可实现双星组合下的静止目标定位.

假设两颗卫星的速度分别为vS1和vS2,目标速度v,则定位方程为

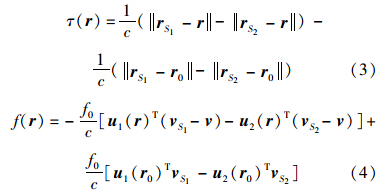
其中,f0表示信号频率;τ(r)和f(r)分别表示目标的DTO和DFO;ui(r),i=1,2,表示卫星i到目标的径向单位矢量;ui(r0),i=1,2，表示卫星i到参考站的径向单位矢量.

目标静止,速度v为零,联立式(2)~式(4),可解算其位置;目标移动,速度v的径向分量给DFO的测量引入较大偏差,若仍以静止目标处理,将出现几百甚至上千公里的定位误差[8].

2 检测算法 2.1 定位一致性检测算法

目标的运动状态检测,就是确定目标速度是否存在,即假设检验问题:

无论哪种假设,同步三星时差定位体制均可实现目标定位,而双星定位技术只有在目标静止时才能完成定位.即目标静止时,同步双星、三星两种方式的定位结果应一致,反之则存在较大差异.

首先,分析三星定位结果的误差分布,掌握目标真实位置所在区域.

目标高程信息相对卫星高度可忽略,通过坐标旋转,可得到正东、正北方向定位误差drS与地固坐标系下定位误差dr的关系:

其中λ和φ为三星定位结果对应的经度和纬度.

将式(1)等式两边取微分,得

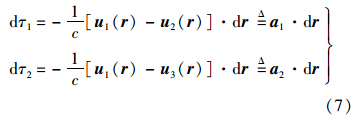
结合式(6)、式(7),得到定位误差与时差测量精度的关系:

其中

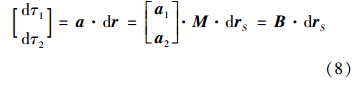
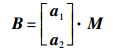
令P为drS的协方差矩阵,则

其中,στi,i=1,2，是时差估计误差标准差,可由时/频差联合估计时的互模糊函数相关输出信噪比估计得到[12,13];σ2E和σ2N为正东、正北方向定位误差方差.

drS服从高斯分布[14,15],其概率密度函数为

显然(ξ－m)TP-1(ξ－m)≤k表示一个椭圆及其内部,定位结果落入此椭圆的概率为

化简可得

由于时差估计误差标准差στi,i=1,2，为实数,则式(9)所示drS的协方差矩阵P为二阶实对称矩阵,其两个特征值均为实数,并且对应的特征向量正交.其特征值λ1,λ2为

假设单位化后的两特征向量为ex,ey,其可构成新坐标系(ex,ey),λ1和λ2则是单位矢量ex和ey上的投影,对应椭圆标准方程的长、短半轴平方.结合概率要求,新坐标系下的误差椭圆见图 2.

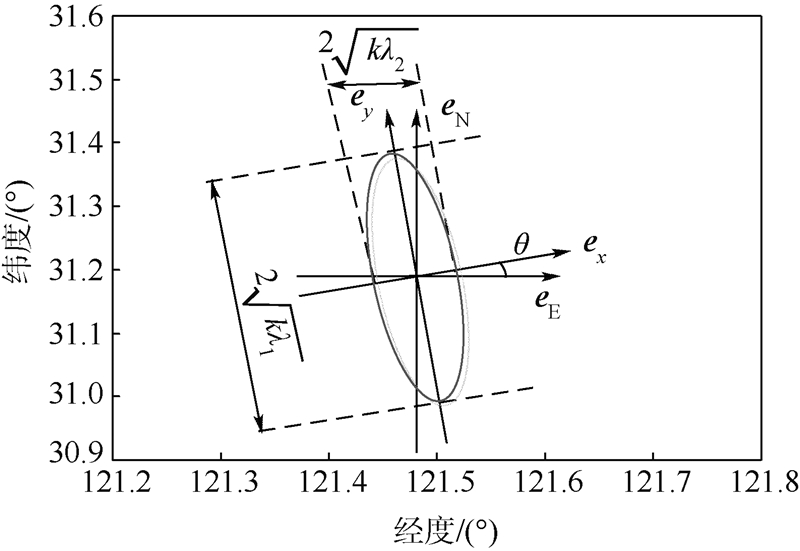图 2 误差椭圆示意图 Fig. 2 Schematic diagram of error ellipse
图选项

其表达式为

设正东、正北方向单位矢量为eE,eN,为便于计算误差椭圆覆盖区域的坐标.可认为新坐标系(ex,ey)是由原坐标系(eE,eN)旋转θ得到：

可得

以σx和σy表示式(14)所示误差椭圆的长、短半轴,则其代表了ex和ey方向上的定位误差标准差.由于正态分布99.7%样本集中在3倍标准差以内,故要覆盖目标真实位置,将其扩展为3σx和3σy,本文定义其为扩展误差椭圆.

综上,定位一致性检测算法的步骤概括如下:

步骤1 输入三星定位结果r、卫星星历和时差估计误差的标准差στi,i=1,2;

步骤2 由式(9)求得协方差矩阵P;

步骤3 根据概率要求(如99.99%),由式(12)得到k;

步骤4 3倍扩展式(14)所示误差椭圆的长、短半轴σx和σy,得到扩展误差椭圆;

步骤5 利用式(16)求得θ,将扩展误差椭圆反向旋转,得到目标真实位置所在区域坐标Se;

步骤6 统计静止假设下目标真实位置区域Se对应的频差范围[L,H];

步骤7 将定位时刻对应的频差观测值与频范围[L,H]比较.超出范围,则判定为移动目标,否则即为静止目标. 2.2 检测性能理论分析

由前所述,定位一致性检测算法的检测概率等于频差观测值超出上述方式获得的频差范围的概率,下面推导其表达式.

在同步卫星和目标位置确定的前提下,假设目标速度大小为v,两颗同步卫星S1,S2与目标连线OS1,OS2的夹角为θ,目标运动方向与目标和两卫星连线的夹角分别为α和β,如图 3所示.

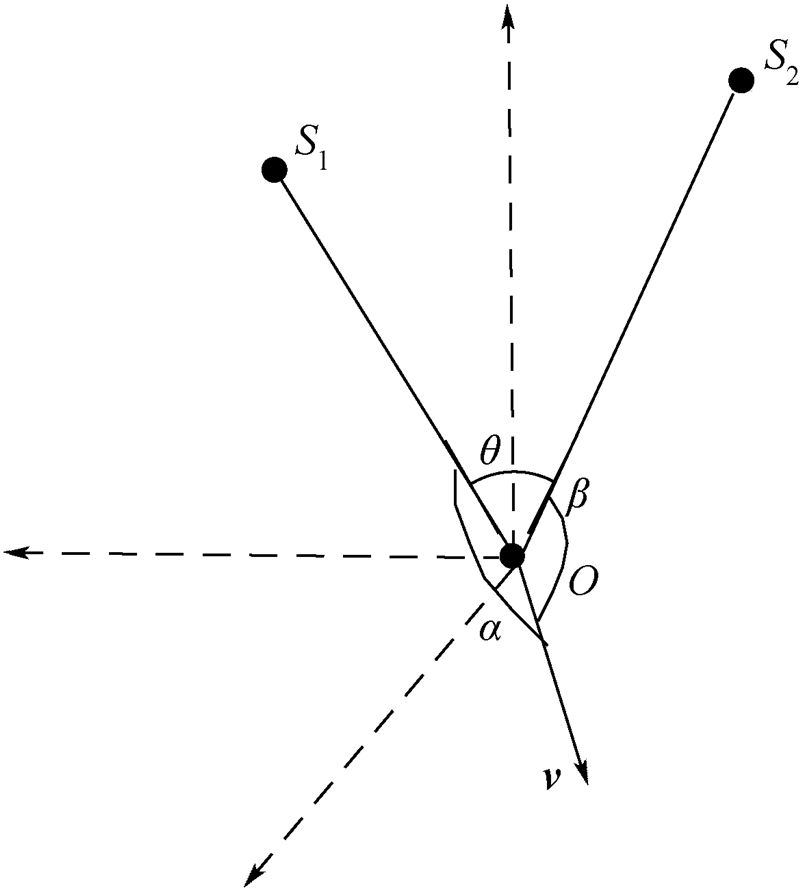图 3 目标与卫星几何关系 Fig. 3 Geometrical relationship of target and satellites
图选项

由于天线旁瓣泄漏的信号功率随着旁瓣角增加而急剧降低,能同时接收到目标辐射源信号的两同步卫星与目标间的夹角θ通常不会太大.另外,目标的运动方向存在约束性,多在地球切面方向附近,而卫星相对目标的仰角较大.不失一般性,假设θ≤40°,α服从[π/3,2π/3]的均匀分布.α一旦确定,运动方向可能是以OS1为轴旋转360°中的任一方向,显然,此时目标运动方向与OS2的夹角β服从[α－θ,α+θ]的均匀分布.

那么,x=cos α的概率密度函数为

由于β的条件概率密度函数为

则y=cos β的条件概率密度函数为

速度引入的额外频差为

根据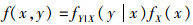可得式(20)所示额外频差的概率分布为

其中

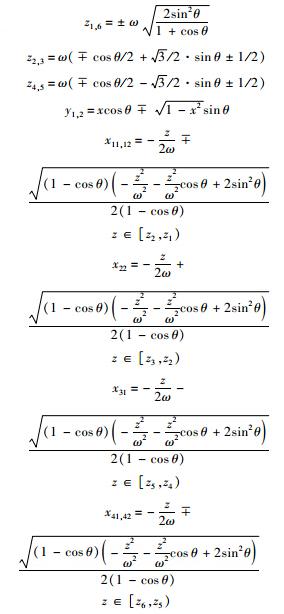
式(21)难以获得解析表达式,可利用数值积分求解.

按照前面描述的检测算法的步骤,根据频差范围统计可得一高一低两个检测门限:

其中,fd(r)为静止假设下的频差公式,即v=0的式(4);Se为分析所得的目标真实位置所在区域.

频差观测值落入两门限值之外的概率即为检测概率:


3 仿真与试验分析 3.1 仿真分析

利用2013-04-24T16:38:00—16:48:00的3颗同步卫星星历仿真,其轨道根数如表 1所示.

表 1 3颗同步卫星星历 Table 1 Ephemeris of three geostationary satellites
卫星编号 轨道根数
a/km e i/(°) ω/(°) Ω/(°) M/(°)
25 40414 7200.000 5631.374 8342.1174.7797.67
31 80014 7210.000 2920.009 6140.23256.3661.69
35696147190.000 1450.006 2274.2591.62258.28
注:a—轨道半长轴;e—轨道离心率;i—轨道倾角;Ω—升交点赤经;ω—近地点幅角;M—平近点角.
表选项

仿真条件:假设目标信号频率6 GHz,目标位置、速度大小v、时/频差估计误差标准差σDTO/σDFO确定,目标的运动方向随机产生,根据目标和卫星的相对位置和速度,计算理论的时差/频差值,并叠加随机误差.利用本文提出的定位一致性检测(LCD,Location Consistency Detection)算法，文献［10]提出的拟合度检验(FD,Fit Detection)和Rao检测(RD,Rao Detection)方法分别进行10 000次蒙特卡洛仿真,统计各自的检测概率.其中,FD和RD方法需利用多组时/频差观测结果,设观测时间间隔为60 s,观测组数N=10,虚警概率Pfa=5%.

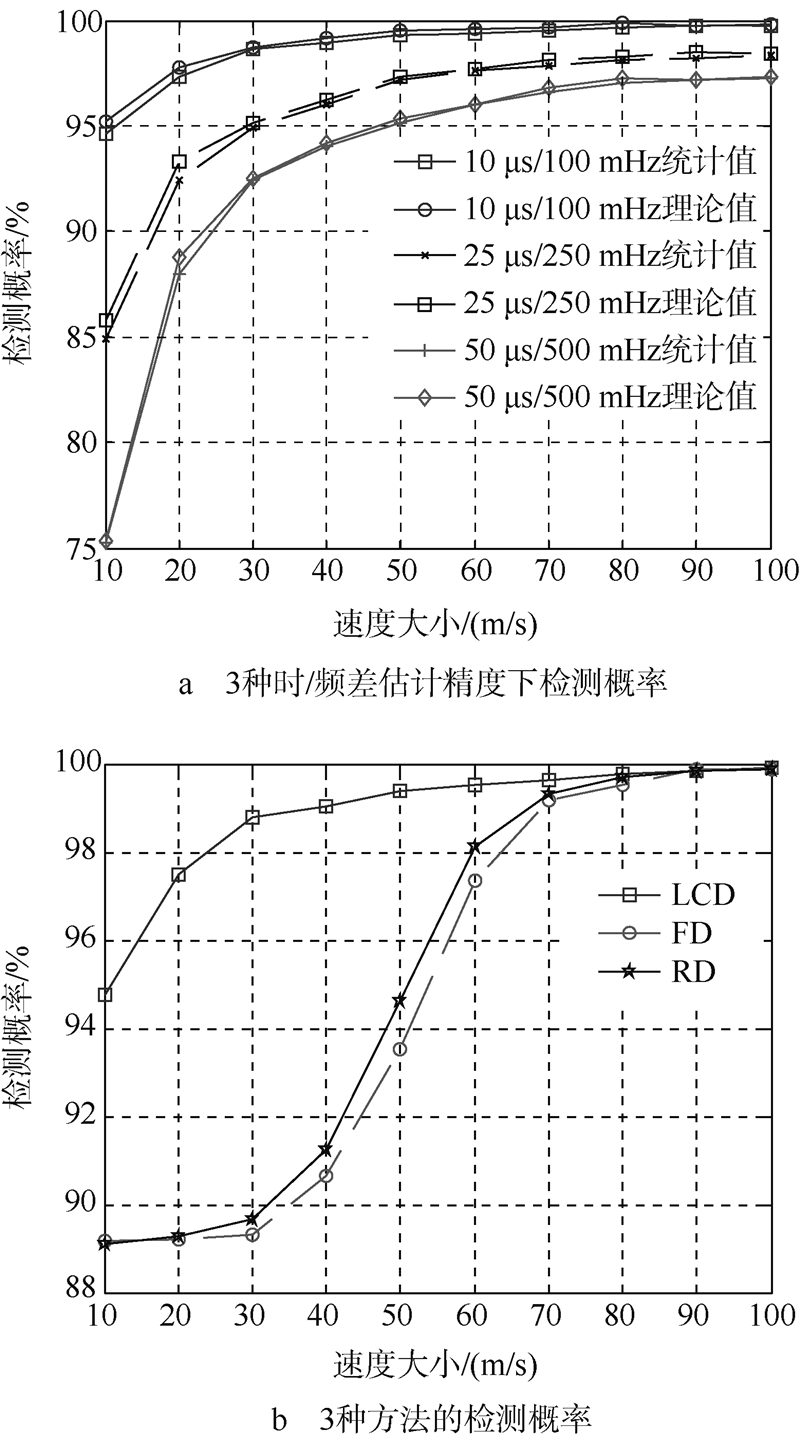
图 4a给出了10 μs/100 mHz,25 μs/250 mHz,50 μs/500 mHz 3种时/频差估计误差标准差条件下,基于本文方法统计得到的检测概率和计算得到的理论检测概率随速度大小变化的曲线.可见,统计值与理论值十分吻合,并且检测概率随着速度的增大和时/频差参数估计精度的提高而增加.因为:①目标速度变大,引入的额外频差变大,超出静止假设下理论频差范围的概率相应增加;②参数估计精度的提高,定位精度提高,误差椭圆变小,对应的理论频差范围,也即检测门限更为准确和精细,检测概率得以提高.

图 4 检测概率随速度变化曲线 Fig. 4 Curves of detection probability vs velocity
图选项

图 4b为时/频差估计误差标准差10 μs/100 mHz时,基于一组参数测量的LCD算法和基于10组参数测量,观测时间约10 min的FD与RD方法的检测概率随速度大小的变化曲线.对比可知,LCD算法检测性能明显高于FD和RD方法,只有当目标速度大于80 m/s时,后两者的检测概率才能接近前者.同时,LCD算法仅需一次参数测量,可做到实时检测,而FD和RD则需利用多组测量结果.故在准确性和时效性方面,本文算法均更出色.

另由图 4可见,本文算法在时/频差估计误差标准差10 μs/100 mHz时,对速度大于20 m/s的目标,检测概率高于97%;速度大于40 m/s的目标,检测概率高于99%. 3.2 试验分析

利用某星载无源定位系统于2013-05-24对某静止目标和2013-10-17对某移动目标的实测数据,基于本文算法进行运动状态检测试验.

图 5给出了系统对静止和移动目标约10 min持续时间的实际定位结果.由于定位几何的原因,移动目标定位结果聚集性反而更好,直接从定位结果难以辨别目标是否移动.

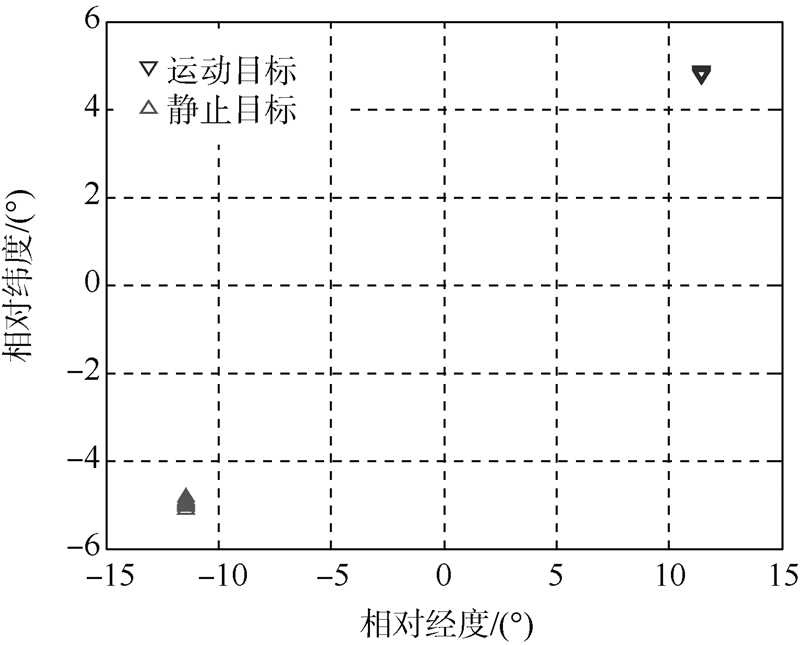图 5 系统对某移动和静止目标定位结果 Fig. 5 Location results of system for moving and stationary targets
图选项

利用本文算法对两目标进行处理,可实现100%的检测区分.

图 6、图 7给出了两个目标的检测结果示意图.为便于说明,图中展示了双星定位结果,而检测过程实际并不需要完成双星定位.图中误差椭圆是利用系统定位结果,参与定位的同步卫星星历,以及根据时差提取过程中互模糊函数的相关输出信噪比大小计算得到的时差估计误差标准差,按照本文方法的步骤1~步骤5计算所得.

图 6 静止目标运动状态检测结果 Fig. 6 Motion state detection results of the stationary
图选项

图 6为静止目标的检测结果:总共16个双星定位点均被包含在误差椭圆内,即每个双星定位点和对应的三星时差定位点相一致,故16次检测均表明目标静止.图 7则是移动目标检测结果,由于目标速度引入了额外频差,导致频差线出现偏离,12个双星定位点沿着时差线散落分布在目标真实位置以外的区域,而没有任何双星定位点落入定位误差椭圆内,即12次结果均成功反映了目标的移动性.因此,本文算法在实际应用中有效.

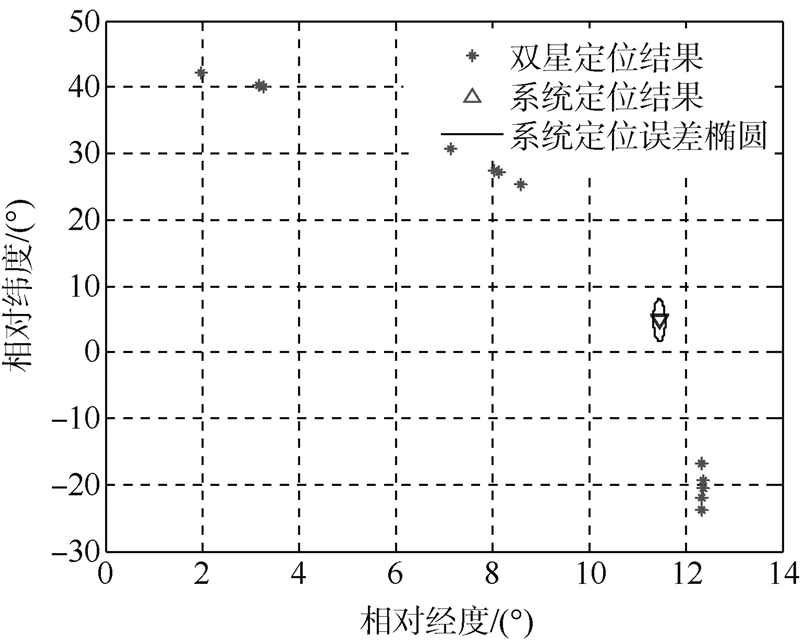图 7 移动目标运动状态检测结果 Fig. 7 Motion state detection results of the moving target
图选项
4 结 论

定位误差大、目标位置变化在定位结果中不能及时体现和观测时间不足等因素,制约了星载无源定位系统目标运动状态检测的准确性和时效性.本文在三星双时差定位结果及其误差特性的基础上,利用星载平台自身运动的特点,引入频差观测量,发挥了双星组合不能对移动目标成功定位的“特点”,提出基于定位一致性的目标运动状态快速检测算法,给出其检测概率理论表达式.仿真和试验结果表明该算法时效性强、检测概率高:仅需一次测量便可完成检测,时/频差估计误差标准差10 μs/100 mHz的条件下,目标速度大于20 m/s时,检测概率高于97%;目标速度大于40 m/s时,检测概率高于99%.

此外,对于检测出的运动目标,可在以系统定位结果为原点的东北天坐标系中,将目标天向速度分量约束为零,进而利用两组频差方程,实现目标速度解算.若能获得多个时刻的时/频差测量结果,还可利用扩展卡尔曼滤波算法对目标位置和速度进行更准确地估计.目前,本文研究成果已成功应用于某星载无源定位系统,实现了目标运动状态的实时检测.

参考文献
[1] Ho K C, Chan Y T.Solution and performance analysis of geolocation by TDOA[J].IEEE Transactions on Aerospace and Electronic Systems,1993,29(4):1311-1322
Cited By in Cnki (8)
[2] 李文华. 三星构型设计与时差定位精度研究[J].宇航学报,2010,31(3):701-706 Li Wenhua.Research on configuration of tri-satellites and location precision of TDOA[J].Journal of Astronautics,2010, 31(3): 701-706(in Chinese)
Cited By in Cnki (0)
[3] Liu K, Chan F,So H C.Semidefinite programming approach for range-difference based source localization[J].IEEE Trans on Signal Processing,2009,57(4):1630-1633
Cited By in Cnki (5)
[4] Yang K, An J P,Xu Z.A quadratic constraint total least-squares algorithm for hyperbolic location[J].International Journal of Communications,Networks and System Sciences,2008,1(2):130-135
Click to display the text
[5] Beck A, Stoica P,Li J.Exact and approximate solutions of source localization problems[J].IEEE Trans on Signal Processing,2008,56(5):1770-1778
Click to display the text
[6] 常啸鸣,张晓林, 张强.基于加权矩阵的TDOA多站无源定位算法[J].北京航空航天大学学报,2011,37(11): 13781383 Chang Xiaoming,Zhang Xiaolin,Zhang Qiang.Method of TDOA multistation passive location based on weighted matrix[J].Journal of Beijing University of Aeronautics and Astronautics,2011,37(11):1378-1383(in Chinese)
Cited By in Cnki (3)
[7] 袁罡,陈鲸. 无源时差定位系统的静止目标聚类检测算法[J].电子与信息学报,2010,32(3):728-731 Yuan Gang,Chen Jing.A clustering detection algorithm of stationary target for passive time difference location system[J].Journal of Electronics & Information Technology,2010,32(3):728-731(in Chinese)
Cited By in Cnki (6)
[8] Ulman R J, Gerantiotis E.Motion detection using TDOA and FDOA measurements[J].IEEE Transactions on Aerospace and Electronic Systems,2001,37(2):759-764
Click to display the text
[9] Pattison T, Chou S I.Sensitivity analysis of dual-satellite geolocation[J].IEEE Transactions on Aerospace and Electronic Systems,2001,36(1):56-71
[10] 魏合文,夏畅雄, 叶尚福.双星定位系统中目标移动性检测与仿真[J].系统仿真学报,2007,19(11):2543-2573 Wei Hewen,Xia Changxiong,Ye Shangfu.Motion detection and simulation in dual-satellite geolocation system[J].Journal of System Simulation,2007,19(11):2543-2573(in Chinese)
Cited By in Cnki (6)
[11] 夏畅雄, 叶尚福,王俊辉.卫星干扰源定位系统中卫星星历校正技术[J].宇航学报,2008,29(3):860-863 Xia Changxiong,Ye Shangfu,Wang Junhui.Ephemeris determination in satellite interference location system[J].Journal of Astronautics,2008,29(3):860-863(in Chinese)
Cited By in Cnki
[12] 严航,朱珍珍. 基于积分抽取的时/频差参数估计方法[J].宇航学报,2013,34(1):95-105 Yan Hang,Zhu Zhenzhen.Fast algorithm for joint estimation of DTO and DFO based on integrate-and-dump filters[J].Journal of Astronautics,2013,34(1):99-105(in Chinese)
Cited By in Cnki
[13] 严航,叶尚福, 朱珍珍.基于解调分选的时分多址信号时/频差参数联合估计方法[J].宇航学报,2013,34(4): 531538 Yan Hang,Ye Shangfu,Zhu Zhenzhen.Algorithm for joint estimation of DTO and DFO for TDMA signals based on signal demodulation and sorting[J].Journal of Astronautics,2013, 34(4): 531-538(in Chinese)
Cited By in Cnki
[14] Torrieri D J. Statistical theory of passive location systems[J].IEEE Transactions on Aerospace and Electronic Systems,1984,AES-20(2):183-198
Click to display the text | Cited By in Cnki (0)
[15] 王艳永,杨功流, 袁二凯,等.四维引导定位TSEP精度评估方法[J].北京航空航天大学学报,2013,39(7):875-879 Wang Yanyong,Yang Gongliu,Yuan Erkai,et al.TSEP positioning accuracy evaluation approach applied in 4D guidance[J].Journal of Beijing University of Aeronautics and Astronautics,2013,39(7):875-879(in Chinese)
Cited By in Cnki (1)
http://dx.doi.org/10.13700/j.bh.1001-5965.2013.0631 北京航空航天大学主办。
0

文章信息

杨宇翔, 张汇川
Yang Yuxiang, Zhang Huichuan
同步三星目标运动状态快速检测方法
Fast algorithm of motion state detection based on tri geo-satellites
北京航空航天大学学报, 2014, 40(10): 1392-1398
Journal of Beijing University of Aeronautics and Astronsutics, 2014, 40(10): 1392-1398.
http://dx.doi.org/10.13700/j.bh.1001-5965.2013.0631

文章历史

收稿日期：2013-11-5
网络出版日期: 2014-03-13

相关文章

工作空间