表1(Table 1)
回归分析是应用极其广泛的数据分析方法之一,经常用于预报、控制等问题.值得注意的是,随着信息采集工具在各领域的充分使用,“数据爆炸”的趋势变得越来越明显.在许多领域,数据的到达呈现出快速、连续的特点[1],并且往往需要系统进行实时的反馈,如网站访问、网络安全信息监测[2]等.在这种情况下,以往针对大数据的批量学习(batch learning),会耗费大量的时间与空间资源,而增量学习(incremental learning)[3]是在充分利用已有数据的基础上,对原有的知识模型进行更新、修正与加强,将更适合海量数据下需要快速反映的情形.对广泛使用的回归模型运用增量式计算有着重要的意义.
Syed等[4]1999提出了衡量增量算法的一个重要标准是能否正确处理概念漂移(concept drift)的问题.有效的增量算法必须保证具有一定的稳健性、计算结果的改进性,以及可恢复性.Gaber等[5]将增量算法分为了基于数据的算法和基于任务的算法两种类型.基于数据的算法主要是采用原数据的某个较优的子集,或者原数据的某种汇总形式进行下一步的增量计算,主要包括样本抽样(sampling)[6]、流数据抽样(load shedding)[7]、草图抽样(sketching)[8, 9]、概要数据结构(synopsis data structures)、聚合表示(aggregation)[10]等.这种方法必须对原数据集的结构进行检验,无法保证选取样本的均衡性.基于任务的算法主要包括近似算法(approximation algorithms)[11]、滑动窗口(sliding window)[8]、算法输出粒度(algorithm output granularity)[12]等,实现相对复杂.
现有的增量算法基本集中在机器学习或计算机领域[13],并已经取得了丰硕的研究成果[14, 15],在实际中的应用也日益广泛[16].而文献对于统计学领域方法的增量算法讨论较少.统计学中的大样本性质都是在样本容量趋于无穷情形下得到的,在目前的技术条件下搜集和存储数据使得样本容量可以无限大.在这种大数据背景下,对传统统计方法的增量运算进行探讨和研究,具有重要的实际应用价值.
本文提出了一种多元线性回归模型的增量算法,可以正确处理概念漂移的问题,并且与用全部数据计算相比,使用了相同量的信息,可以达到同等的精度.算法只需要存储原数据的叉积矩阵,对于变量维度不是很大的数据集,可以大大节省存储空间,缩短数据的载入和传输的时间,提高计算效率.文中给出了基于叉积阵的检验统计量的增量算法,最后通过仿真实验说明了多元线性回归的增量算法的有效性. 1 多元线性回归模型的增量算法 1.1 多元线性回归分析
在多元线性回归分析中,记因变量为Y,自变量集合为X={x1,x2，…,xp},样本容量为n;记第i个样本在第j个变量的观测值为xij(i=1,2,…,n;j=1,2,…,p).
根据自变量和因变量的样本数据,定义矩阵:
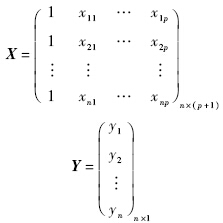
进而定义增广矩阵:
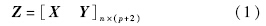
增广矩阵的叉积阵为
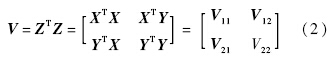
多元线性回归模型的最小二乘估计量可用叉积阵表示:
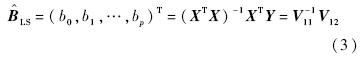
关于模型及估计质量的评价指标可表示为
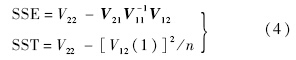
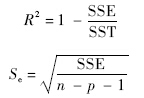
由此可见,多元线性回归分析的关键在于:利用样本数据计算增广矩阵及其叉积阵,利用叉积阵求出回归系数的估计值以及模型的评价指标. 1.2 最小二乘估计的增量算法
在高斯-马尔科夫定理的假设条件下,最小二乘估计是最佳线性无偏估计量.本节探讨最小二乘估计量的增量算法.
在回归分析中,根据已有样本可以得到系数向量的最小二乘估计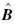
.实际数据处理中,经常会出现得到系数的估计后,又增加了新的样本,需要对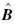进行更新.这时便需要引入增量算法.
记新增加的样本为
采用增广矩阵进行表示为
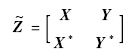
而叉积矩阵则为
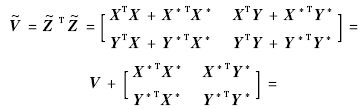
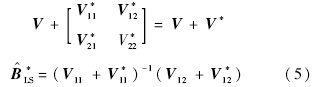
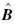时已经得到V11,V12,不需要重新进行计算,只需计算V*11,V*12.由于利用增量算法,可以省去V11,V12的计算,这在已用样本容量n很大时,可以节约大量资源.尤其是只有少量新增样本时,增量计算可以体现更大的优势.
事实上,在进行回归分析时,最小二乘估计是从增广矩阵的叉积阵出发进行模型的估计,并非完全从原始数据出发.因此,采用增量算法时,完全可以对V11,V12进行存储;当有了新增样本时,直接对新增样本部分进行计算,然后再计算更新的回归系数向量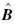.如此处理,避免了对已有样本[X Y]的重复读取.由于在海量样本情形下,V11,V12的大小要远远小于[X Y]的大小,从而可以大大节约读取数据的时间和占用的内存空间.
1.3 模型检验的增量算法
容易知道,线性模型的F检验和t检验的统计量分别可以表示为
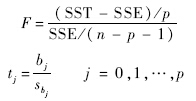
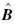LS的第j个元素;sbj=Secjj,cjj是矩阵V-111对角线上第j个元素.在考虑有新增样本情形时,
,
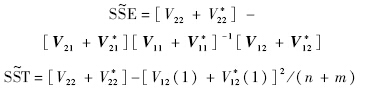
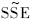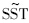均可以基于叉积阵V~计算得到,无需对前n个样本重新进行计算;基于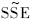,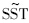容易构造
,
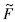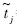等统计量:
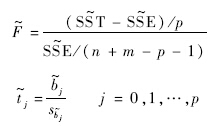
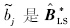的第j个元素;
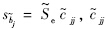是矩阵[V11+V*11]-1对角线上第j个元素.如此,基于叉积阵本文得到了F检验和t检验的增量算法. 1.4 其他估计量的增量算法
在1.2节最小二乘估计的增量算法分析过程中,本文仅利用了叉积阵的相关信息.由此可知,基于叉积阵的估计量都可以利用如此增量算法,如岭回归估计量和加权最小二乘等估计量也可以采用此增量算法.
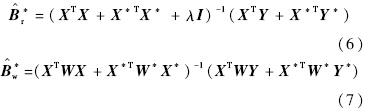
下面进行仿真数据实验,通过数据模拟验证多元线性回归模型增量算法的有效性.
首先,生成3个相互独立且服从标准正态分布的自变量χ1,χ2,χ3.回归系数和常数项均采用(0,2)上的均匀分布生成,得到
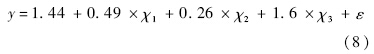
为说明增量算法的适用情形,实验采用了不同的样本量和增量的组合,以比较不同组合下增量算法的效果.在由上述方法生成的5 000 000样本中进行随机抽样,得到样本量分别为(100,1 000,10 000,100 000,200 000,500 000,1 000 000)的数据集,并分别随机抽取每一个数据集的(1%,5%,10%,15%,20%)作为增量,比较使用增量算法和不使用增量算法的时间变化.
实验计算机配置为CPU:3.20 GHz,Intel i5-3470处理器,内存3 556 MB,Windows XP系统.使用Python语言工具,对每种情况分别进行50次独立重复实验,每次独立重复实验的计时结果为连续进行200次计算的时间的加总.表 1为使用增量算法、重复计算50次回归模型系数所用时间的均值与方差.
| 样本量 | 增量 | |||||||||
| 1% | 5% | 10% | 15% | 20% | ||||||
| 均值 | 方差 | 均值 | 方差 | 均值 | 方差 | 均值 | 方差 | 均值 | 方差 | |
| 100 | 10.568 9 | 0.240 0 | 10.671 2 | 0.238 7 | 10.755 6 | 0.697 9 | 10.783 0 | 0.292 2 | 10.813 0 | 0.392 6 |
| 1 000 | 10.642 9 | 0.304 1 | 10.898 1 | 0.235 8 | 11.477 1 | 1.034 5 | 11.477 2 | 0.315 0 | 11.693 8 | 0.289 2 |
| 10 000 | 11.224 5 | 0.283 8 | 13.121 3 | 1.015 2 | 15.195 2 | 0.227 3 | 17.990 0 | 1.326 6 | 23.547 3 | 1.119 5 |
| 100 000 | 18.116 7 | 4.902 4 | 38.030 8 | 2.296 0 | 71.776 3 | 4.987 6 | 106.388 2 | 3.111 1 | 133.911 8 | 1.919 3 |
| 200 000 | 25.214 2 | 5.025 9 | 74.652 4 | 1.709 5 | 134.711 0 | 2.185 3 | 194.796 8 | 2.982 1 | 257.517 8 | 7.332 4 |
| 500 000 | 37.928 1 | 3.405 5 | 165.379 1 | 3.492 1 | 321.290 5 | 5.225 8 | 496.232 6 | 9.952 4 | 689.754 5 | 12.310 9 |
| 1 000 000 | 76.153 9 | 2.126 9 | 320.243 3 | 5.386 3 | 322.993 0 | 12.732 1 | 689.663 9 | 14.807 0 | 1 137.985 5 | 15.297 0 |
图 1中的10条曲线表示非增量方法与增量方法下,当样本的增量所占原样本比例分别为(1%,5%,10%,15%,20%)时,不同的样本量下计算回归模型系数所用时间的差异.回归模型叉积矩阵的计算复杂度是随着样本量线性增加的,从图 1中可以看出非增量算法的实验结果也反映了计算时间的线性增长趋势.而采用增量算法,计算所用时间受样本量影响较小.所以在样本量较大时,计算效率较非增量算法会有明显提高.
 |
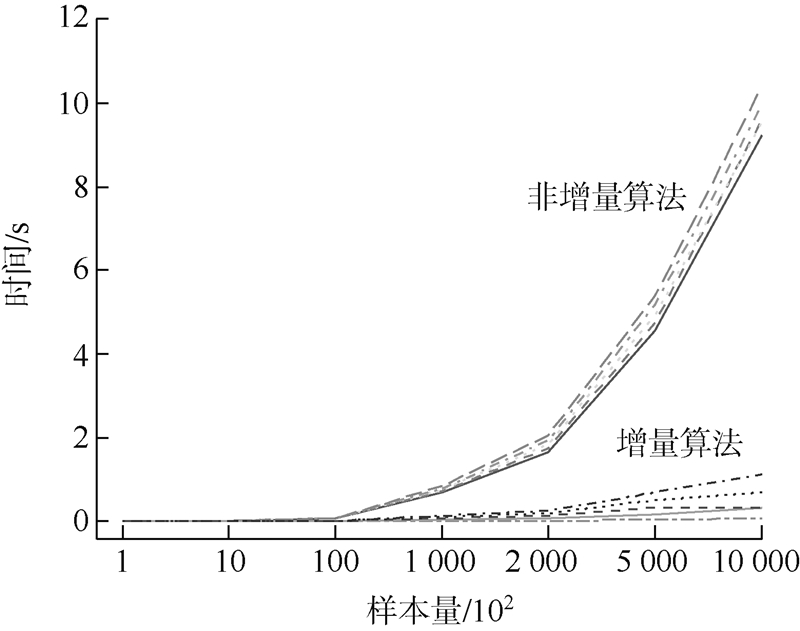| 图 1 回归系数的非增量算法与增量算法计算时间对比图Fig. 1 Comparison chart for the time in calculating coefficients between traditional method and incremental method |
类似地,图 2和图 3分别为回归模型F检验和t检验在两种算法下所用时间的对比图.从图中可以看出,在原样本数量大于10 000时,增量的方法均开始体现出明显的优势.并且随着样本量的增加,增量方法的优势将进一步增大.
 |
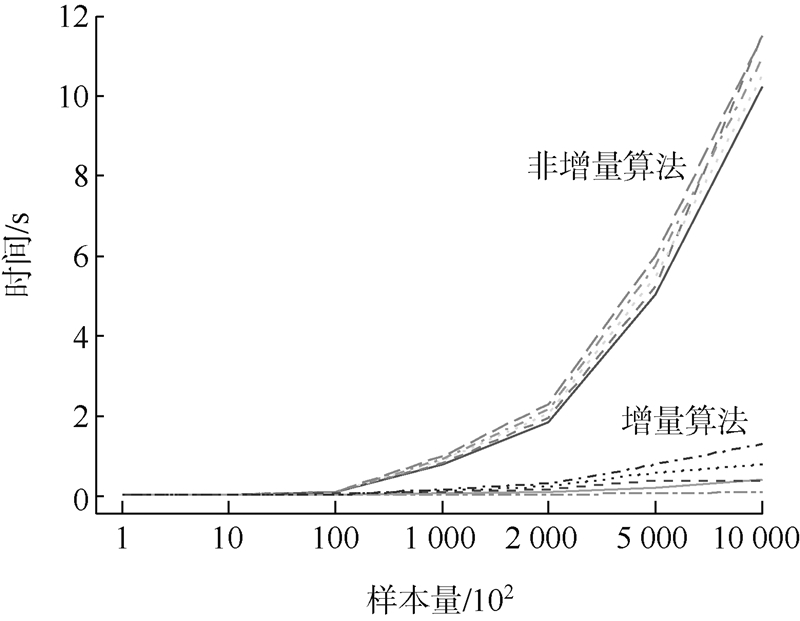| 图 2 检验的非增量算法与增量算法计算时间对比图Fig. 2 Comparison chart for the time of F-test between traditional method and incremental method |
 |
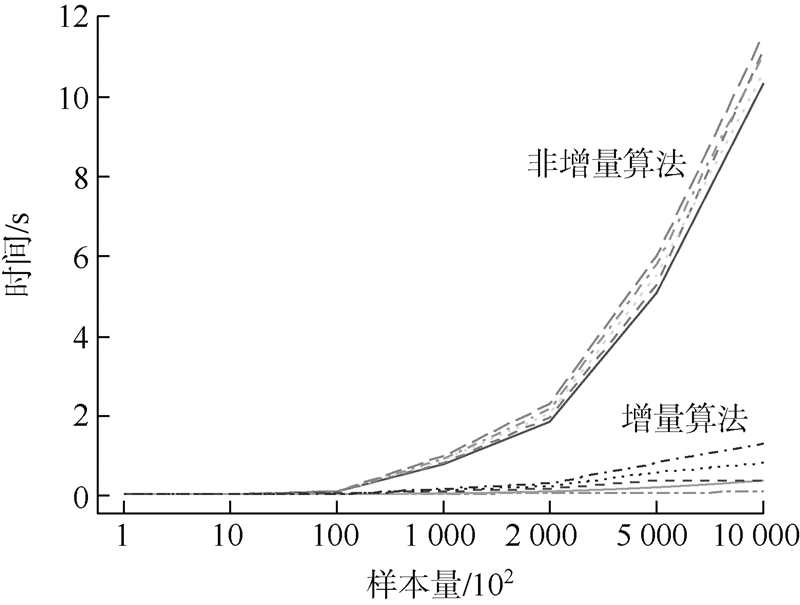| 图 3 检验的非增量算法与增量算法计算时间对比图Fig. 3 Comparison chart for the time of t-test between traditional method and incremental method |
本文从统计的视角,提出了一种多元线性回归模型的增量算法,得到以下主要结论:
1) 该增量算法可以用在基于叉积阵求解的各种统计检验量的计算中,如最小二乘回归估计、t检验和F检验统计量、岭回归估计量和加权最小二乘估计等.
2) 该增量算法只需要存储原数据的叉积矩阵,可以节省大量的存储空间及数据载入时间,加快运算效率.
3) 在线性回归建模过程中,本文的增量方法运用了全部的数据信息,与使用全部数据建模具有完全相同的结果.最后,通过数据仿真实验,证明了算法的有效性.
| [1] | Tomczak J M,Gonczarek A.Decision rules extraction from data stream in the presence of changing context for diabetes treatment[J].Knowledge and Information Systems,2013,34(3):521-546 |
| Click to display the text | |
| [2] | Yang L,Cao J N,Tang S J,et al.A framework for partitioning and execution of data stream applications in mobile cloud computing[C]//IEEE Fifth International Conference on Cloud Computing.Washington,DC:IEEE Computer Society,2012:794-802 |
| Click to display the text | |
| [3] | Coppock H W,Freund J E.All-or-none versus incremental learning of errorless shock escapes by the rat[J].Science,1962,135(3500):318-319 |
| Click to display the text | |
| [4] | Syed N A,Liu H,Sung K K.Handling concept drifts in incremental learning with support vector machines[C]//Proceedings of the Fifth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.San Diego,CA:ACM,1999:371-321 |
| Click to display the text | |
| [5] | Gaber M M,Zaslavsky A,Krishnaswamy S.Mining data streams:a review[J].ACM Sigmod Record,2005,34(2):18-26 |
| Click to display the text | |
| [6] | Domingos P,Hulten G.A general method for scaling up machinelearning algorithms and its application to clustering[C]//Proceedings of the Eighteenth International Conference on Machine Learning(ICML 2001).Williams College,Williamstown,MA:Morgan Kaufmann,2001:106-113 |
| Click to display the text | |
| [7] | Babcock B,Datar M,Motwani R.Load shedding techniques for data stream systems[C]//The 2003 Workshop on Management and Processing of Data Streams.San Diego,CA:ACM,2003 |
| Click to display the text | |
| [8] | Papapetrou O,Garofalakis M,Deligiannakis A.Sketch-based querying of distributed sliding-window data streams[J].Proceedings of the VLDB Endowment,2012,5(10):992-1003 |
| Click to display the text | |
| [9] | GAMA J.Data stream mining:the bounded rationality[J].Informatica,2013,37(1):21-25 |
| [10] | Nath S,Venkatesan R.Publicly verifiable grouped aggregation queries on outsourced data streams[C]//Data Engineering(ICDE),2013 IEEE 29th International Conference on.Washington,DC:IEEE Computer Society,2013:517-528 |
| Click to display the text | |
| [11] | Muthukrishnan S.Data streams:algorithms and applications[M].Hanover,MA:Now Publishers Inc,2005 |
| [12] | Krishnaswamy S,Gama J,Gaber M M.Mobile data stream mining:from algorithms to applications[C]//Mobile Data Management(MDM),2012 IEEE 13th International Conference on.Washington,DC:IEEE Computer Society,2012:360-363 |
| Click to display the text | |
| [13] | 肖智,王明恺,谢林林.基于支持向量机的大学生助学贷款个人信用评价[J].清华大学学报:自然科学版,2006,46(S1):1120-1124 Xiao Zhi,Wang Mingkai,Xie Linlin.Personal credit evaluation of college student loans with support vector machines[J].Journal of Tsinghua University:Science and Technology,2006,46(S1):1120-1124(in Chinese) |
| Click to display the text | |
| [14] | Babcock B,Babu S,Datar M,et al.Models and issues in data stream systems[C]//Proceedings of the Twenty-first ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems.Madison,WI:Association for Computing Machinery,2002:1-16 |
| Click to display the text | |
| [15] | Golab L,Ozsu M T.Data stream management [J].Synthesis Lectures on Data Management,2010,2(1):1-73 |
| [16] | 姚远.海量动态数据流分类方法研究[D].大连:大连理工大学,2013 Yao Yuan.The research on massive and dynamic data stream classification method[D].Dalian:Dalian University of Technology,2013(in Chinese) |
| Cited By in Cnki |
