Turbo码由于其优越的性能,已被空间数据系统咨询委员会(CCSDS,Consultative Committee for Space Data System)组织列为深空通信和卫星通信的标准之一,CCSDS规范定义的Turbo码支持5种信息帧长度,分别是1 784,3 568,7 136,8 920,16 384 bit,其中,前4种均为223 bit的整倍数,主要用于和CCSDS所定义的RS(255,223)编码保持格式上的统一,最后一种长度16 384 bit用于支持高速的数据传输[1].
对于规范所支持的223 bit整倍数的帧长,已有现成的商用IP Core以及大量的研究成果[2].但是,实际的应用环境对编码帧长需要有更灵活的选择.比较典型的取值是将信息数据帧的长度确定为255 bit的整数倍(而不是223),这样,比较容易获得一个完整数据帧长为2的N次方的长度(例如:4倍255 bit再加4 bit同步字节即1 024 bit).本文所要实现的Turbo码编译码器,根据特殊应用的要求,对其支持的信息数据帧长度进行了扩展,不但需要支持规范所确定的4种帧长,同时包括16 384 bit范围内的其他帧长. 1 Turbo编码参数及译码算法 1.1 编码参数
CCSDS规范中,对遥测信道编码器中使用的Turbo码进行了定义.Turbo码的一般参数如下[3].
码型(code type):Systematic Parallel concatenated turbo code;
分量编码器个数:2组;
分量编码:递归卷积码;
分量编码状态:16个;
平均码率:r=1/2,1/3,1/4,或1/6(可选);
信息帧长度:k=1 784,3 568,7 136,8 920,16 384 bit.
另外,交织器参数是Turbo码非常重要的一项参数,为了达到兼容标准参数的目的,本文基本参照CCSDS规范中的算法进行交织计算. 1.2 译码算法
MAP方法是衡量接收序列中,单个符号判决的最佳估计,目的是使译码输出比特错误概率最小[4].MAP译码算法的一个主要特点就是实现了迭代译码.由于有外部信息的参与,信噪比一定时,误码率会随着译码迭代次数增加而减小.循环次数达到一定数目时,译码性能不再有特别明显的提高,此时,可以停止迭代计算,整理输出译码结果[5, 6].
log-MAP算法是MAP算法的对数化形式,将MAP算法中的变量都转换为对数形式,从而把乘法运算转换为加法运算[7].同时译码器的输入输出相应地修正为对数似然比形式,再对算法进行必要的修改就得到了log-MAP算法.
SW-MAP算法与MAP算法的主要区别是将数据帧分成多个数据块,译码针对长度为D(小于数据帧长度)的数据块进行,在接收到D个信道符号后开始译码[8, 9]. 2 软件设计与算法实现 2.1 算法实现框图
MAP算法的实现具有一定的复杂性,另外两种算法则是在其基础之上进行改进而来,MAP算法基本框架图如图 1所示.
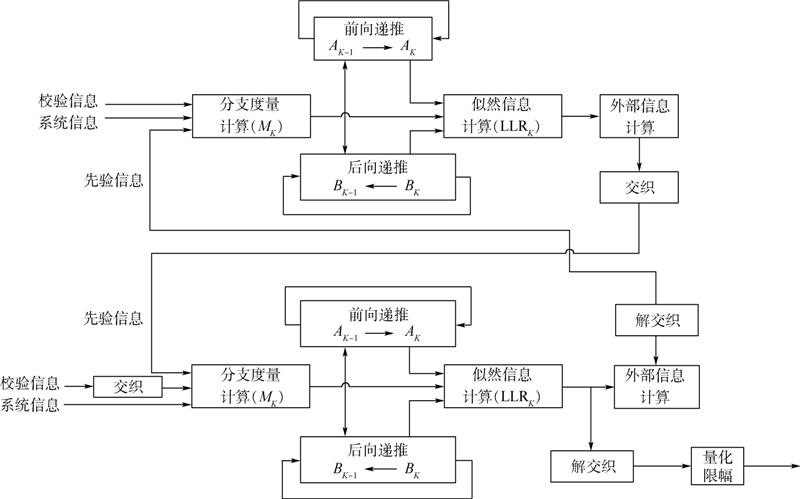 |
| 图 1 算法实现框图Fig. 1 Block diagram of algorithm |
本文中Turbo码编译码算法MAP,log-MAP和SW-MAP算法均用C++实现,并且程序以动态链接库的形式存在,然后编写Python测试程序,改变相应的参数,通过仿真测试各项译码性能.仿真环境框图如图 2所示.
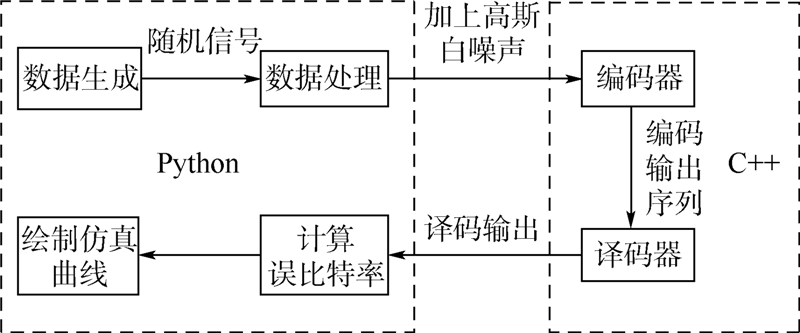 |
| 图 2 仿真环境框图Fig. 2 Block diagram of simulation |
测试过程中能改变的相关参数主要包括:码率、信息帧长度、信噪比、仿真起始点、仿真步长、最大半迭代次数、出错帧数、SW-MAP算法中的窗格大小.
测试的最终结果是要绘制出特定参数和算法下的信噪比(SNR,Signal Noise Ratio)与误码率(BER,Bit Error Rate)的关系曲线图. 3 仿真结果分析 3.1 通用性检测
本文所设计的编译码器主要特点之一就是具有通用性,除CCSDS标准参数外,还要覆盖非标准参数.就整个实现过程而言,编译码器的各项参数及性质都不存在明显的跳跃性和突变,因此仿真前可以根据实际情况和经验做出评估,对于码长相近的标准与非标准参数,此款编译码器所表现出来的译码性能应该非常接近.
采用MAP算法,对1 784,2 040,8 920,8 160 bit的帧长进行编译码仿真,r=1/2,迭代次数为20次.仿真结果如图 3所示.
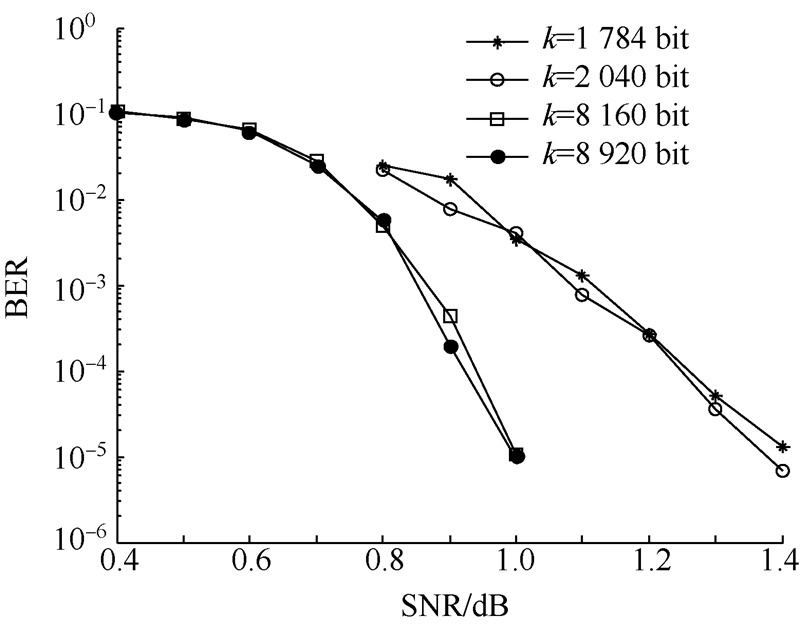 |
| 图 3 通用性检测MAP算法仿真图Fig. 3 Commonality test result in MAP algorithm |
仿真时,选取了两组长度相近的标准和非标准参数的信息序列,分别为1 784(223×8)bit和2 040(255×8)bit,8 920(223×5×8)bit和8 160(255×4×8)bit.同时,保持其他各项参数如码率、迭代次数等一致.
以文献[10, 11]中对标准参数进行的仿真结果作为参考,可以证实,上述仿真中符合CCSDS标准参数的序列长度(即k=1 784 bit和k=8 920 bit)的译码结果是符合实际情况的,具有一定参考价值.而从上述仿真数据可以看出,非标准参数的信息序列和与其长度相近的标准信息序列的译码性能非常接近.由此可以从一定程度上说明,本文所设计的编译码器具有通用性,不仅能够覆盖标准参数,也能实现非标准参数的译码. 3.2 不同算法的性能比较
本文选用MAP,SW-MAP,log-MAP算法对4 080 bit帧长进行仿真测试,r=1/3,迭代次数为20次. 仿真结果如图 4所示.
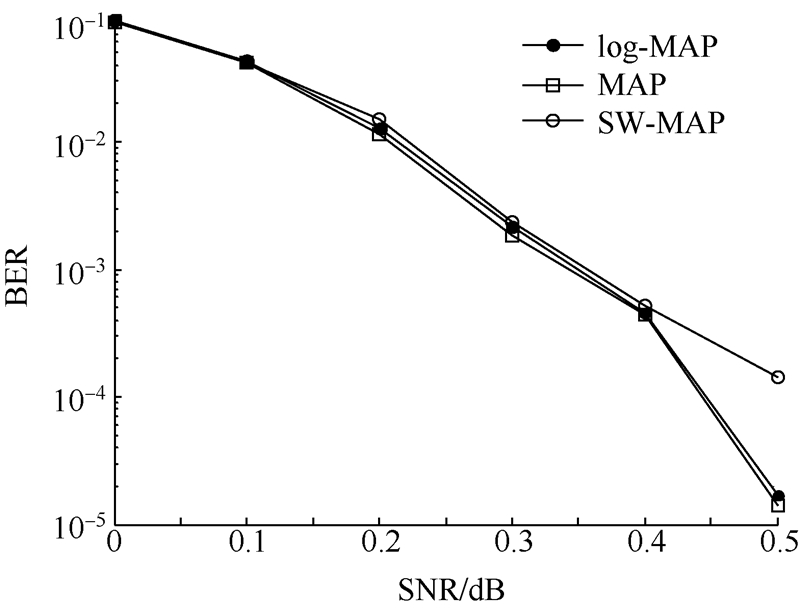 |
| 图 4 不同算法仿真比较图Fig. 4 Comparison of different algorithms |
可以明显看出,3种算法中,MAP算法的译码性能较好,log-MAP算法与MAP算法的性能非常接近,而SW-MAP算法则略差.尤其是当信噪比升高时,3种算法的差异性表现得愈加明显.MAP算法的复杂度最高,是最原始最准确的译码算法.而log-MAP算法则是通过对数运算实现将乘法转换为加法,为硬件实现做准备,其软件仿真性能与MAP算法非常接近[12].SW-MAP算法特点在于以牺牲部分译码性能来换取减少延时[13].在一次迭代中,MAP算法整体递归,对于其中两个重要的中间变量——前向递推联合条件概率α和后向递推联合条件概率β,只需设定一次初始值;而SW-MAP算法分块递归,每个分块都无法再利用前一个块的结果,需重新设定初始值,因而形成累积误差,从而导致SW-MAP译码性能的降低.
在实际应用中,应根据需求选择合理的译码算法,既能保证译码性能达到相应标准,又要使得算法复杂性在能接受的范围之内. 3.3 参数值对译码性能的影响
1) 不同信息序列长度对Turbo码译码性能的影响.
信息序列长度是影响Turbo码的误码率在10-6~10-2之间性能的关键因素.本文选用MAP算法,对2 040,4 080,6 120,8 160 bit的帧长进行仿真,r=1/3,迭代次数为20次. 仿真结果如图 5所示.
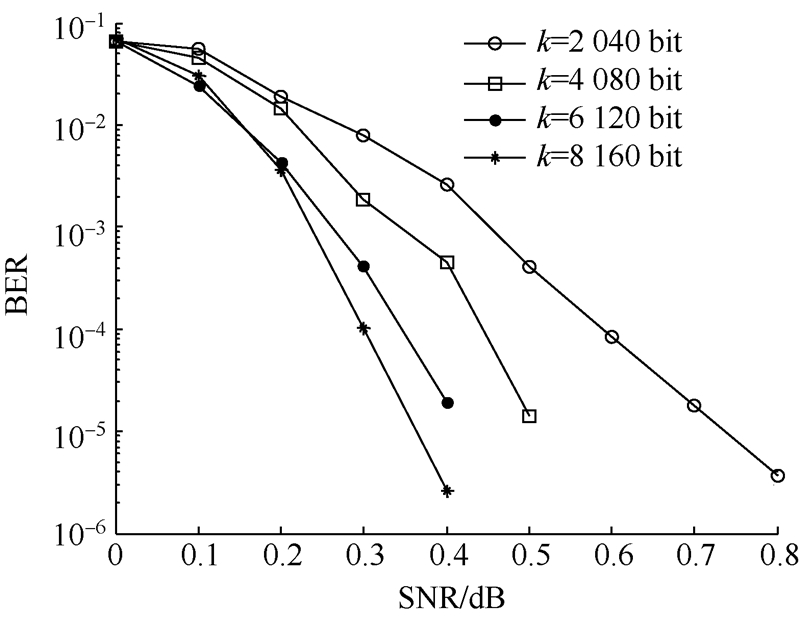 |
| 图 5 不同帧长比较图(MAP算法)Fig. 5 Comparison of different frame sizes in MAP algorithm |
可以看出,在一定范围内,信息序列长度越长,误码率越低.并且,当信噪比较低时,信息序列长度对误码率影响不是很大,但是当信噪比逐渐增大时,增加信息序列长度就能很明显地提高译码性能.
在发送端,其伪随机性是由交织器以及并行级联方式来实现的.在接收端,各译码器输出的外信息之所以能被互相利用进行多次迭代来增强纠错能力,还得归功于交织和解交织器的置乱作用[14].在CCSDS参数中,交织块的长度取决于信息序列长,因此,信息序列越长,则交织的伪随机性越充分,外信息的交换越能发挥作用,从而提高译码性能.
2) 码率对Turbo码译码性能的影响.
选用不同的码率,通常会对译码性能造成很大影响.本文选用MAP算法,对2 040 bit帧长进行1/2,1/3,1/4,1/6 4种码率的编译码仿真,迭代次数为20次.仿真结果如图 6所示.
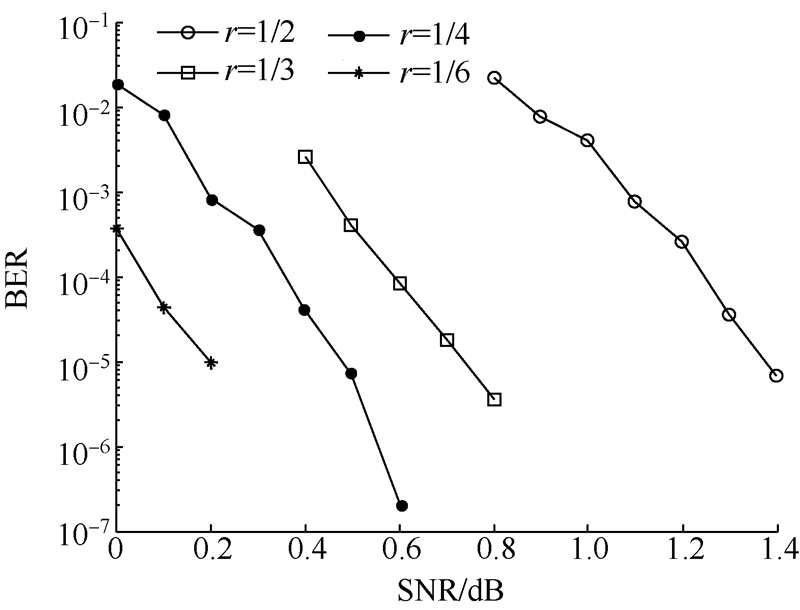 |
| 图 6 不同码率比较图(MAP算法)Fig. 6 Comparison of different bitrates in MAP algorithm |
仿真过程中,保证信息序列长度、算法、迭代次数等其他参数全部相同,选用1/2,1/3,1/4,1/6共4种码率.从上述一组仿真结果可以得到结论:在其他条件相同的情况下,码率越小,即编码长度越长,Turbo码译码性能越好,而且这种差异性表现得非常明显.
Shannon编码定理指出:如果采用足够长的随机编码,就能逼近Shannon信道容量.这个仿真结果正好是符合香农编码定理的,当然编码长度的增加也会增大译码的复杂性,因此也应当根据实际情况,合理地选择码率,既保证译码性能,又使得计算复杂度在可接受的范围内[15].
3) 不同迭代次数对Turbo码译码性能的影响.
Turbo码通过迭代译码来提高译码性能,因此译码次数是决定Turbo码译码性能的关键性因素之一.通过仿真来考察迭代次数对Turbo码译码性能的影响.
本文选用MAP算法,对4 080 bit帧长进行仿真,r=1/3,迭代次数n分别设置为5,10,15,20次. 仿真结果如图 7所示.
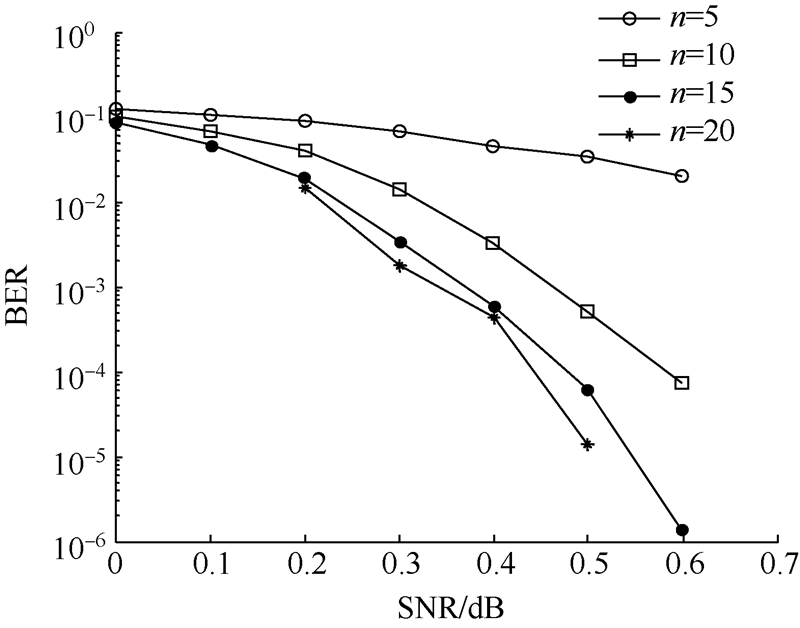 |
| 图 7 不同迭代次数仿真图Fig. 7 Comparison of different iterations in MAP algorithm |
从图 7的仿真结果可以看出,在一定范围内,随着迭代次数的增加,Turbo码误码率不断下降,性能趋于更优;并且,信噪比越高,这种影响越明显.在BER≥10-2时,迭代次数对译码误码率影响比较小;在10-6≤BER≤10-2时,迭代次数增加,使得外信息多次交换,得到充分利用,从而显著改善译码性能.但是,当迭代次数增加到一定数目时,对于译码性能的提高已经没有特别明显的促进作用了,继续进行迭代所带来的增益是非常小的,反而会增加译码计算复杂度[16].因此,在译码时不能盲目地加大迭代次数,而应该根据实际需求选择合理的参数. 4 结 论
综上,可以得出如下结论:
1) 所实现的Turbo码译码器,具备通用性,对于CCSDS非标准参数也能实现正常编译码.
2) Turbo码3种较为典型的译码算法中,log-MAP算法仅仅只是对数据做了对数处理,因此译码特性与MAP算法相近,而SW-MAP算法由于涉及多处分段设定初始值,因而引起误差,译码特性略差.
3) 参数的设置对于译码性能有着重要的影响.在一定范围内,帧长越长,码率越低,迭代次数越高,则Turbo码译码性能越好.
有关Turbo码更多的性质和功用,还需进一步深入的探讨.
| [1] | Berrou C,Glavieux A.Near optimum error correcting coding and decoding:Turbo-codes[J].Communications,IEEE Transactions on,1996,44(10):1261-1271 |
| Click to display the text | |
| [2] | Divsalar D,Pollara F.Turbo codes for deep-space communications[R].TDA Progress Report 42-121,1995,42:66-77 |
| Click to display the text | |
| [3] | Studer C,Benkeser C,Belfanti S,et al.Design and implementation of a parallel turbo-decoder ASIC for 3GPP-LTE[J]. IEEE Journal of Solid-State Circuits,2011,46(1):8-17 |
| Click to display the text | |
| [4] | CCSDS 101.0-B-6 Telemetry channel coding[S] |
| [5] | Vucetic B,Yuan J.Turbo codes:principles and applications[M].Dordrecht:Kluwer Academic Publishers,2000:12-14 |
| [6] | Bahl L R,Cocke J,Jelinek F,et al.Optimal decoding of linear codes for minimizing symbol error rate[J].IEEE Transactions on Information Theory,1974,IT-20(2):284-287 |
| [7] | 刘东华,梁光明.Turbo码设计与应用[M].北京:电子工业出版社,2011:24-27 Liu Donghua,Liang Guangming.Turbo design and application[M].Beijing:Publishing House of Electronics Industry,2011:24-27(in Chinese) |
| [8] | 王新梅,肖国镇.纠错码——原理与方法(修订版)[M].西安:西安电子科技大学出版社,2002:12-15 Wang Xinmei,Xiao Guozhen.Error correction code:principle and method(revised edition)[M].Xi'an:Xidian University Press,2002:12-15(in Chinese) |
| [9] | Halunga S V,Vizireanu N,Fratu O.Imperfect cross-correlation and amplitude balance effects on conventional multiuser decoder with turbo encoding[J].Digital Signal Processing:A Review Journal,2010,20(1):191-200 |
| Click to display the text | |
| [10] | Hanzo L L,Liew T H,Yeap B L,et al.Turbo coding, Turbo equalisation and space-time coding:EXIT-chart-aided near-capacity designs for wireless channels[M].New Jersey:John Wiley & Sons,2011:11-12 |
| [11] | 李涛护,李建东,周旭.CCSDS标准的Turbo译码器的硬件设计[J].无线电工程,2006,35(11):59-61 Li Taohu,Li Jiandong,Zhou Xu.Implementation and simulation of CCSDS Turbo-codes decoder in hardware[J].Radio Engineering,2006,35(11):59-61(in Chinese) |
| Cited By in Cnki (1) | |
| [12] | Douillard C,Jezequel M,Berrou C,et al.Iterative correction of intersymbol interference:Turbo-equalization[J].European Transactions on Telecommunications,1995,6(5):507-511 |
| Click to display the text | |
| [13] | EI Gamal H,Hammons A R Jr.Analyzing the turbo decoder using the Gaussian approximation[J].IEEE Transactions on Information Theory,2001,47(2):671-686 |
| Click to display the text | |
| [14] | Sun J,Takeshita O Y.Interleavers for turbo codes using permutation polynomials over integer rings[J].IEEE Transactions on Information Theory,2005,51(1):101-119 |
| Click to display the text | |
| [15] | Lottici V,Luise M.Embedding carrier phase recovery into iterative decoding of turbo-coded linear modulations[J].Communications,IEEE Transactions on,2004,52(4):661-669 |
| Click to display the text | |
| [16] | Pyndiah R M.Near-optimum decoding of product codes:block turbo codes[J].IEEE Transactions on Communications,1998,46(8):1003-1010 |
| Click to display the text |


