目前高超声速飞行器已成为未来国防装备发展和民用空天技术的重要方向,特别是临近空间高超声速飞行器,由于其具备传统航空与航天飞行器所不具备的战略、战术以及效费比方面的优势,是目前各国争夺空天权争相发展的重点,已经成为21世纪世界航空航天领域一个极其重要的发展方向[1].
与传统飞行器相比,高超声速飞行器再入过程中呈现强烈的非线性动态特性和强耦合特性,使得控制系统的研究任务更具挑战性.当前针对高超声速飞行器的控制系统设计普遍采用的是非线性控制方法,如鲁棒控制[2]、滑模自适应控制[3]和神经网络自适应控制[4]以及轨迹线性化(TLC,Trajectory Linearization Control)[5, 6]等方法,由于TLC采用开环控制器(求伪逆)+闭环控制器(跟踪误差稳定调节器)的控制策略,该结构保证了其具有一定的鲁棒性和较强的抗干扰能力,目前已被成功应用于空天飞行器[5, 6]等系统.其中文献[5]提出了基于TLC的X-33再入飞行控制系统设计方法,文献[6]在文献[5]的基础上给出了基于动压的实时调整时变带宽的算法,降低了对执行机构要求的同时却牺牲了系统响应的快速性;当飞行过程中不确定性增加至一定程度时,TLC方法本质上的鲁棒性将会遭到破坏甚至失效.针对此问题,目前的研究成果均采用干扰观测器与控制器结合的设计思路,并取得了较好的控制效果.文献[7]采用非线性干扰观测器+TLC的控制方法,利用观测器的输出来抵消气动参数摄动对系统的影响;文献[8]则结合单隐层神经网络与TLC方法设计了空天飞行器的姿态控制系统,但文献[7, 8]在干扰重构的快速性和准确性方面均有所欠缺.由于滑模干扰观测器(SMDO,Sliding-Mode Disturbance Observer)具有设计简单、易于实现和收敛速度快等优点,近年来受到众多学者的广泛关注.文献[9]针对光盘驱动系统采用SMDO重构了干扰,但设计的干扰重构项包含符号函数,导致了干扰补偿的不连续且存在抖振现象.针对此问题,文献[10, 11]针对飞控系统设计了基于双扭曲算法的SMDO,取得了较好的重构效果.与文献[9]相比,文献[10, 11]的干扰重构抖振现象减弱,但重构项中仍包含符号函数,且算法相对复杂.
为此,针对高超声速飞行器再入段快时变、强耦合以及存在参数不确定和外部干扰情况下的姿态控制问题,同时考虑到执行机构动态和输入受限,首先,结合非线性跟踪微分器,通过对姿态制导指令及其微分信号安排合理的过渡过程,将非线性微分-跟踪器应用于解决过渡过程中执行机构的饱和问题;接着,针对文献[7, 8, 9]中存在的问题,以减少抖振为目标,分别在姿态和角速率回路设计了二阶滑模干扰观测器(SOSMOD,Second Order Sliding-Mode Disturbance Observer),利用符号函数积分来重构内外回路的复合干扰.最后通过仿真比较,验证了本文提出的基于滑模干扰观测器的高超声速滑翔飞行器控制方法的有效性.
1 模型及问题描述本文主要研究再入段高超声速飞行器的大范围机动控制问题,此时发动机已关闭,仅靠气动舵提供操纵力矩.在建模过程中忽略飞行器结构弹性模态的影响,同时充分考虑系统的不确定、建模误差及外部干扰,选取状态变量x1=Ω=[α β μ]T,x2=w=[p r q]T,飞行器的执行机构仅考虑气动舵,控制量δ=[δeδaδr]T,则高超声速飞行器姿态动力学模型可描述如下[12, 13, 14]:
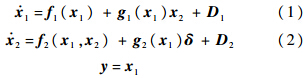
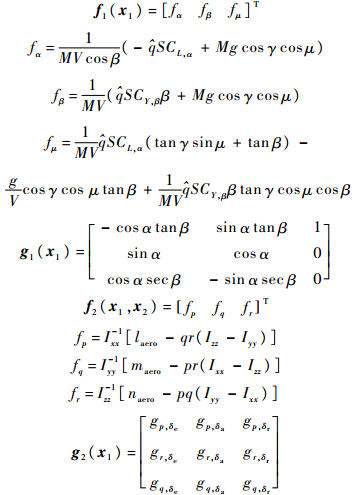
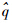为动压;D1=Δf1+Δg1w+ds(t),D2=Δf2+Δg2δ+df(t)为系统的复合干扰;Δf1,Δf2,Δg1,Δg2为不确定性和建模误差;ds(t)和df(t)为外部干扰;gi,j为气动参数项,具体表达形式详见文献[12, 13, 14].控制系统设计的目的是在考虑复合干扰、执行器输入受限的情况下,根据期望的制导指令Ωd设计合适的舵偏角指令δcmd,使得飞行器的姿态角Ω渐进跟踪Ωd.为清晰说明本文的设计思路,其基本原理如图 1所示,本文的控制方案可分为两部分:
 |
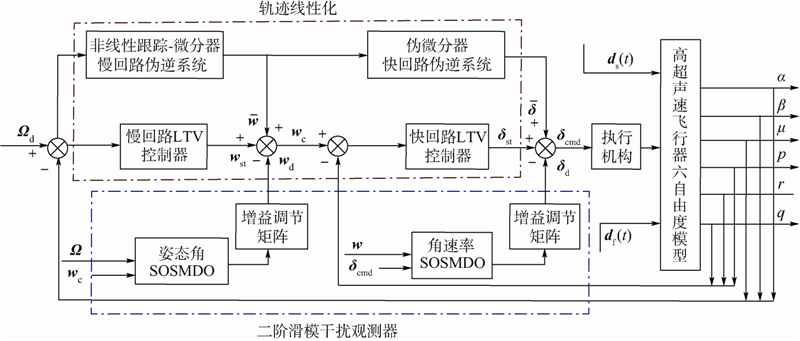| 图 1 基于SMDO-TLC的高超声速飞行器姿态控制Fig. 1 Attitude control for hypersonic vehicle based on SMOD-TLC |
1) 开环伪逆控制中利用韩式跟踪微分器求取姿态回路的标称指令及其微分信号,改善了执行机构过渡期间的控制品质,同时避免了执行机构饱和现象的发生.
2) 针对存在参数不确定和外部干扰情况下的姿态控制问题,以给出能保证姿态稳定跟踪的舵偏角指令为目标,设计了二阶滑模干扰观测器以及补偿控制律.
2 轨迹线性化方法(TLC)简介首先针对形如式(1)的动态系统对TLC方法作简单回顾[2, 3],令D1=0,若标称的系统状态x-,输入u满足:
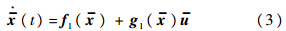
若定义x=x-+e,u=u+ust,则跟踪误差动态特性可描述如下:
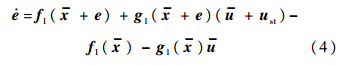
将式(4)沿标称状态和输入(x-,u)的邻域范围内泰勒级数展开可得到:
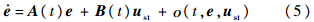
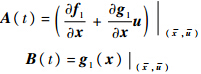
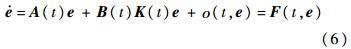
假设1 e=0为式(5)的孤立平衡点,F:[0,∞)×De→Rn,De={e∈Rne
假设2 线性时变系统式(5)中{A(t),B(t)}一致完全可控.
若动态特性方程(4)、方程(6)满足上述假设，则根据文献[2, 3]可利用PD谱理论设计时变反馈控制律ust,使得误差在原点处指数稳定,即系统状态在控制律ust和u的共同作用下以指数形式收敛于期望的标称轨迹状态,记Ac(t)=A(t)+B(t)K(t),显然Ac(t)为赫尔维茨矩阵,则根据文献[13]中例4.21可知存在连续可微、有界的正定对称矩阵P(t),即
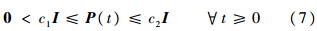
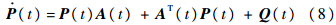
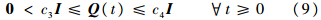
当前轨迹线性化控制系统设计包括以下两个部分:伪微分器的设计以及对非线性标称系统求伪逆;利用PD谱配置方法对误差LTV系统设计时变控制器.通过选取合适的PD谱配置参数,可保证稳态误差指数收敛于原点.详细的设计步骤可参见文献[2, 3],这里不再赘述.
3 基于滑模干扰观测器的TLC设计 3.1 非线性跟踪-微分器设计根据TLC方法的设计思想和步骤,标称控制量可由式(3)推导出:
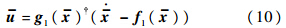
需要注意的是,上式中参与计算的均为状态变量的标称值.式中符号†表示伪逆运算符,其计算表达式为A†=AT(AAT)-1.为了保证系统的因果性,当前TLC方法中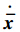
将由x经过如下伪微分器求得[1, 2, 3, 4, 5, 6, 7, 8]
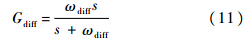
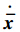,这里不失一般性,令一阶惯性环节的时间常数为T,则指令信号v(t)至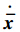的传递函数为
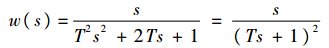
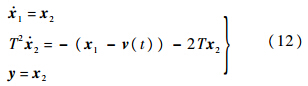
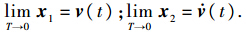
其形式等价于二阶线性积分链式微分器[15],并且T等效于摄动参数ε.当式(12)的状态初始值x1(0)与v(0)有较大误差时,由于微分器的高增益影响,使得初始时刻附近,微分器的导数估计会存在峰值现象.故T足够小时微分信号近似程度较高的同时,过渡阶段会引起标称指令的微分信号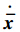乃至标称输入u的剧烈跳变,可见该峰值现象是当前TLC方法无法避免的.
考虑到非线性跟踪-微分器[16]具有根据系统输入能力事先安排过渡过程的优点,并且能够保证过渡过程的快速性且无超调,故可以采用加速度受限的跟踪微分器对姿态制导指令安排过渡过程.这里采用二阶最速离散跟踪微分器[16]:
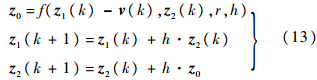
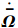,快回路的角速率标称指令w由式(10)直接获取,类似地,标称舵偏指令δ也可通过式(10)求出.
3.2 二阶滑模干扰观测器设计首先给出如下合理的假设.
假设3 复合干扰Di(i∈{1,2})关于时间的偏导数是连续且有界的,且存在已知的有界常数Ci>0满足:
定理1 针对姿态动力学模型式(1)和模型式(2),满足假设3,考虑如下的二阶滑模动态:
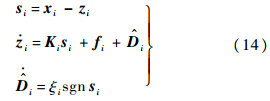
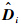i为内外回路观测器对复合干扰的估计,即干扰重构值;
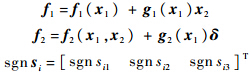
当选取ξi>Ci时,辅助滑模向量si及其导数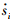
均渐近收敛于原点.
证明 将式(1)和式(2)代入式(14),综合有
对式(14)求导,并代入式(13)可得
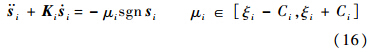
选取如下的Lyapunov函数:
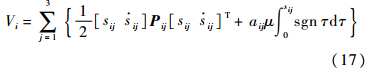
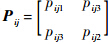为待设计的对称正定矩阵,且满足pij1pij2>p2ij3,pij1=kijpij3,pij2=aij,pij2kij>pij3.对式(17)求导,并代入式(14)及正定参数矩阵Pij可得
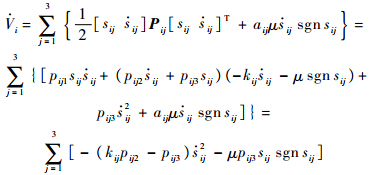
显然当sij≠0或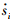ij≠0时,
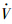i<0,因此二阶滑模观测器的辅助滑模向量si及其导数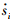均渐近收敛于原点. 证毕
以上证明借鉴了动态滑模控制器的设计思想,将滑模变量si通过微分环节构成新的滑模变量,使得不连续项以积分形式转移至滑模变量的一阶导数中,能够得到在时间上本质连续的干扰重构值,在一定程度上削弱抖振现象.
3.3 姿态及角速率回路控制律设计由于文献[2]已给出基于TLC方法的再入飞行器标称状态下内外回路的非线性飞行控制律,即文献[2]中的式(5)和式(6),本文直接引用如下.
姿态回路:
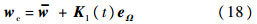
角速率回路:
式(18)和(19)中符号具体表达式详见文献[2],快、慢回路增益矩阵的求取由Ac(t)=A(t)+B(t)K(t)得出,其中Ac(t)为由PD谱理论设计的期望闭环跟踪误差动态特性,A(t)与B(t)均可由MATLAB符号工具箱快速获取.下面针对姿态回路给出补偿控制律,由3.2节可以看出,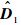
为观测器对复合干扰的估计,定义新的姿态回路控制律为
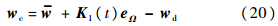
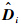为姿态回路的补偿控制律,g-11为增益调节矩阵.将式(20)代入式(1),则式(6)可改写成
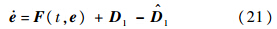
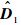,然后根据估计值设计出有效的补偿控制律,以抵消复合干扰对系统的影响.角速率回路的控制律设计方法与此类似,这里不再赘述.
4 稳定性分析记干扰误差重构向量：
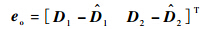
由定理1可知,当选取ξi>Ci时,辅助滑模向量si及其导数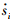均渐进收敛于原点,则由式(14)可知eo将于有限时间内渐进收敛于原点,根据文献[13]定理4.14可知,存在Lyapunov函数Vo(t,e)满足:
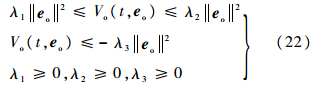
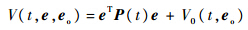
将式(8)和式(20)代入上式,经整理得到:
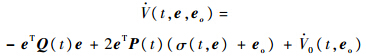
由式(7)和式(9)可知
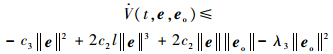
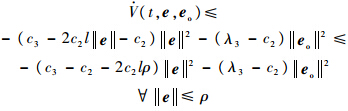
选择ρ<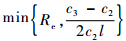
,λ3≥c2,以保证当‖e‖≤ρ时有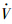(t,e,eo)≤0成立,此时复合系统误差动态特性局部指数稳定.
仿真中高超声速飞行器初始状态选择如下:飞行速度Ma=6.5,飞行高度H=30.9 km,初始姿态角和角速率分别为α0=0°,β0=0.3°,μ0=0°,p0=q0=r0=0 rad/s,姿态制导指令Ωd=[6 0 1 0]T(°),舵偏角限幅以及动态约束为
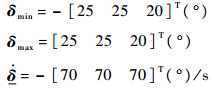
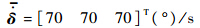
针对执行机构过渡期间的饱和问题,为检验本文方案的合理性,将本文提出的引入非线性跟踪-微分器的轨迹线性化方法与文献[14]的轨迹线性化方法进行仿真比较.其中轨迹线性化方法的设计参数与文献[14]相同,非线性跟踪-微分器选取的参数如下:积分步长h=0.005 s,加速度饱和值的绝对值r=5.73(°)/s2.考虑到控制品质,文献[14]对三通道均设计了指令滤波器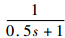
.下面以俯仰通道为例,分别给出无复合干扰情况下本文方案与文献[14]方案的飞行姿态控制系统的仿真曲线，如图 2、图 3所示.
 |
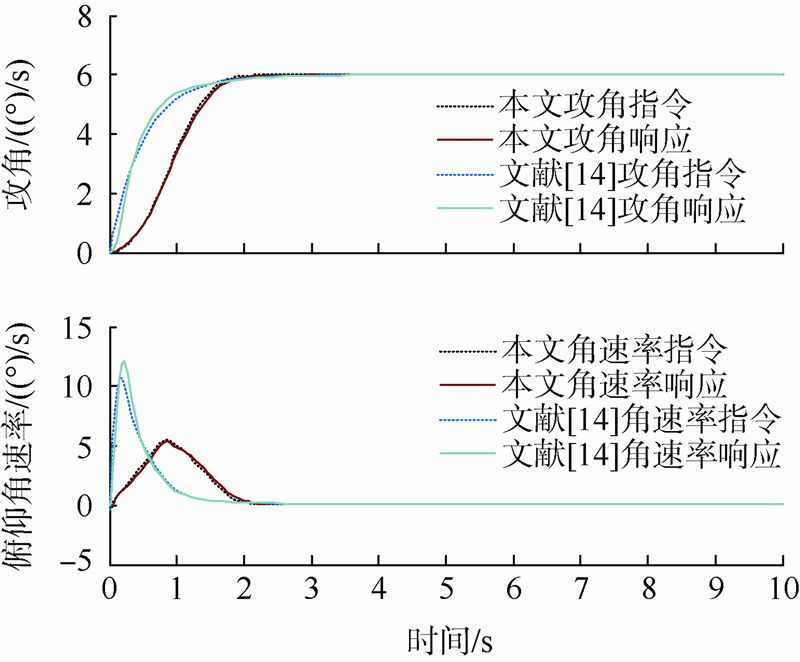| 图 2 两种控制方案的姿态回路响应曲线Fig. 2 Attitude loop response for two control schemes |
 |
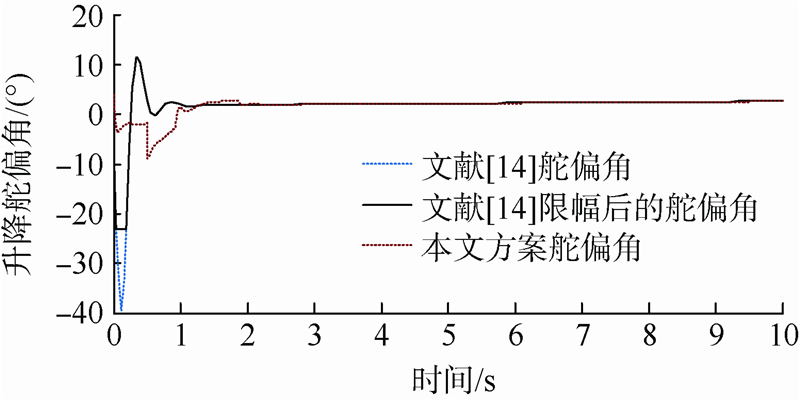| 图 3 两种控制方案的升降舵偏角响应曲线Fig. 3 Deflection angle response for two control schemes |
由上述对比可以看出,在相同的飞行条件和制导指令下,两种控制方案的攻角响应均呈现出较好的动态特性,调节时间均约为2 s,但文献[14]的俯仰角速率响应在过渡期间出现剧烈跳变,导致升降舵偏角迅速跳变至-40°,同时过渡期间存在一定的跟踪误差;相反,由于本文的控制方案中引入了加速度受限的跟踪-微分器,在舵偏角约束范围内合理地安排了角速率的过渡过程,解决了原先TLC方法中的微分信号在过渡阶段的峰值现象;在不牺牲系统的动态特性与跟踪误差的基础上,舵偏量的变化范围约为文献[14]的1/4,因此本文的方案具有更好的控制性能.
5.2 滑模干扰观测器性能仿真
为验证本文设计的二阶滑模干扰观测器对复合干扰的重构效果,以角速率回路为例,三通道的复合干扰分别取时变正弦、时变余弦以及正弦与方波瞬间切换信号,所需的设计参数如下:K2=diag{400,400,400},ξ2=diag{2.1,2.3,2}.为了更好地说明本文设计的观测器的效果,分别与文献[17]提出的非线性干扰观测器(NDO)和文献[10]提出的基于双扭曲算法的SMDO进行了对比,NDO设计参数参考文献[17],即角速率回路的观测器增益l21=l22=l23=50.为减少SMDO的干扰重构抖振,采用滤波器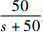
对文献[10]的重构值进行滤波.图 4给出了文献[17]的NDO以及文献[10]的SMDO与本文的SOSMDO的角速率回路复合干扰重构值对比曲线.
 |
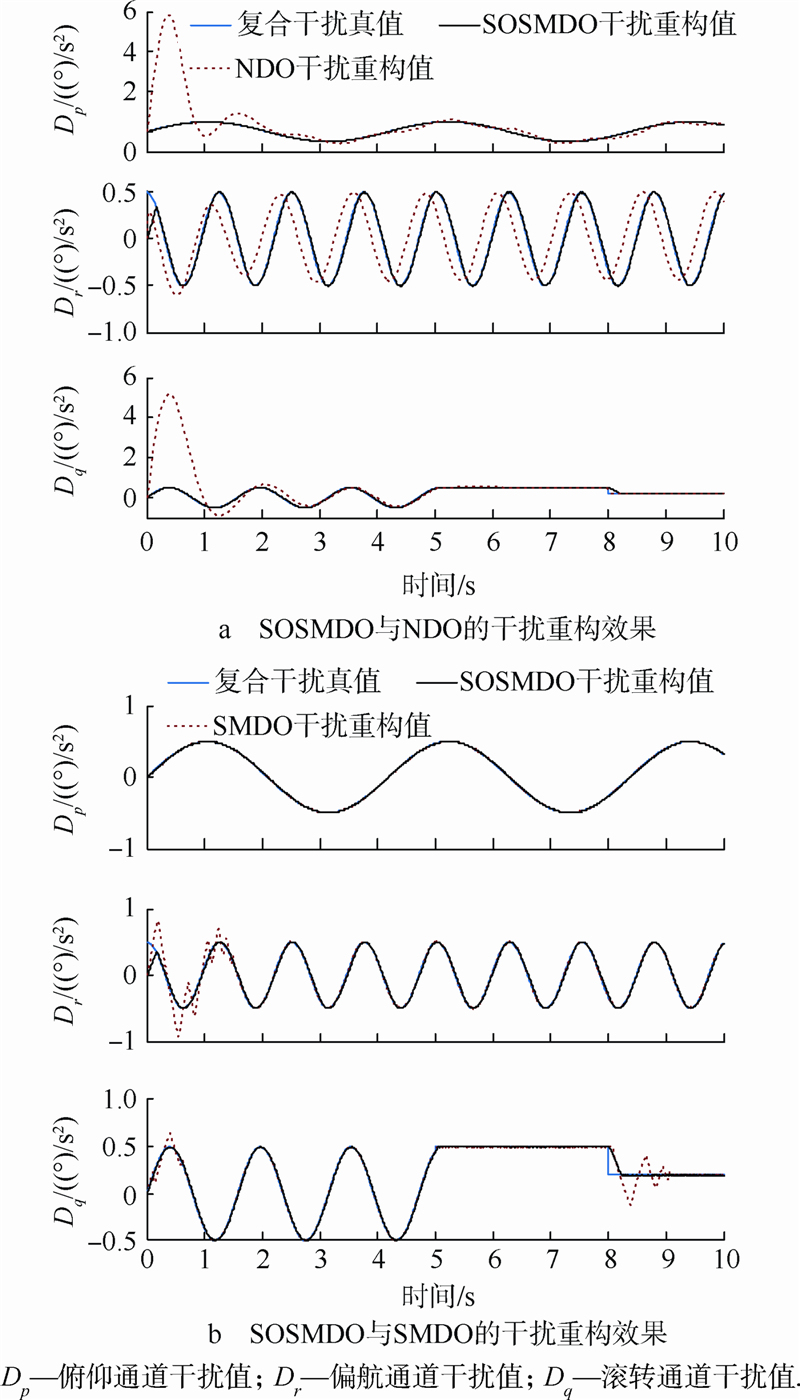| 图 4 角速率回路复合干扰重构效果Fig. 4 Reconstruction effects of disturbances in angular rate loop |
可以看出所设计的SOSMDO与文献[17]的NDO以及文献[10]的SMDO相比,SOSMDO能够迅速重构角速率回路的复合干扰,其动态性能以及重构效果更好,抖动现象得到了充分地抑制.同时,由于NDO重构误差指数收敛,故初始阶段会出现强烈的超调,对于高频干扰,重构存在滞后;SMDO在快变信号瞬间切换处因符号函数的作用会呈现颤振行为.
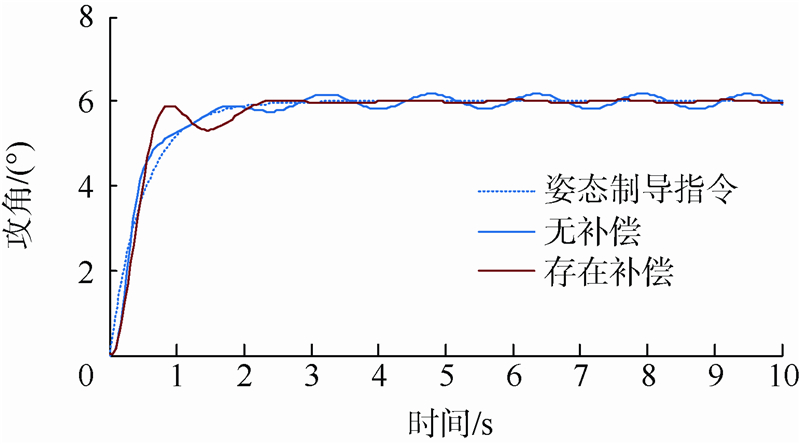
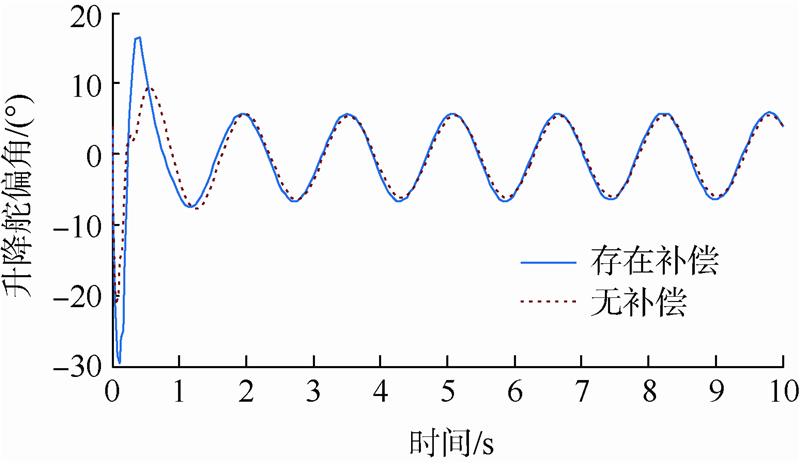
5.3 存在复合干扰情况下的飞行器姿态跟踪控制仿真仿真中假设气动力以及力矩系数存在-60%的不确定性,角速率回路在t=0 s加入外界干扰df(t)=[0.5sin(1.5t),0.5cos(5t),0.5sin(4t)]T,单位为(°)/s2.综合考察控制系统在存在气动参数摄动及外界干扰情况下的控制性能，如图 5~图 8所示.
 |
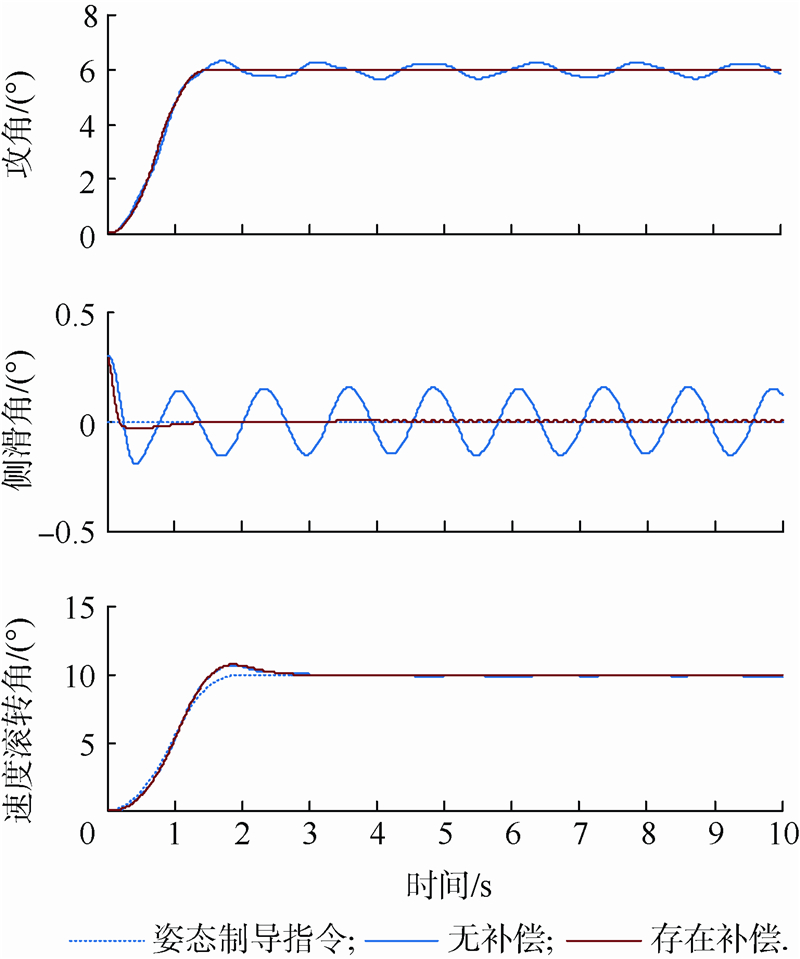| 图 5 存在复合干扰情况下的姿态响应曲线Fig. 5 Attitude response in the presence of compound disturbances |
 |
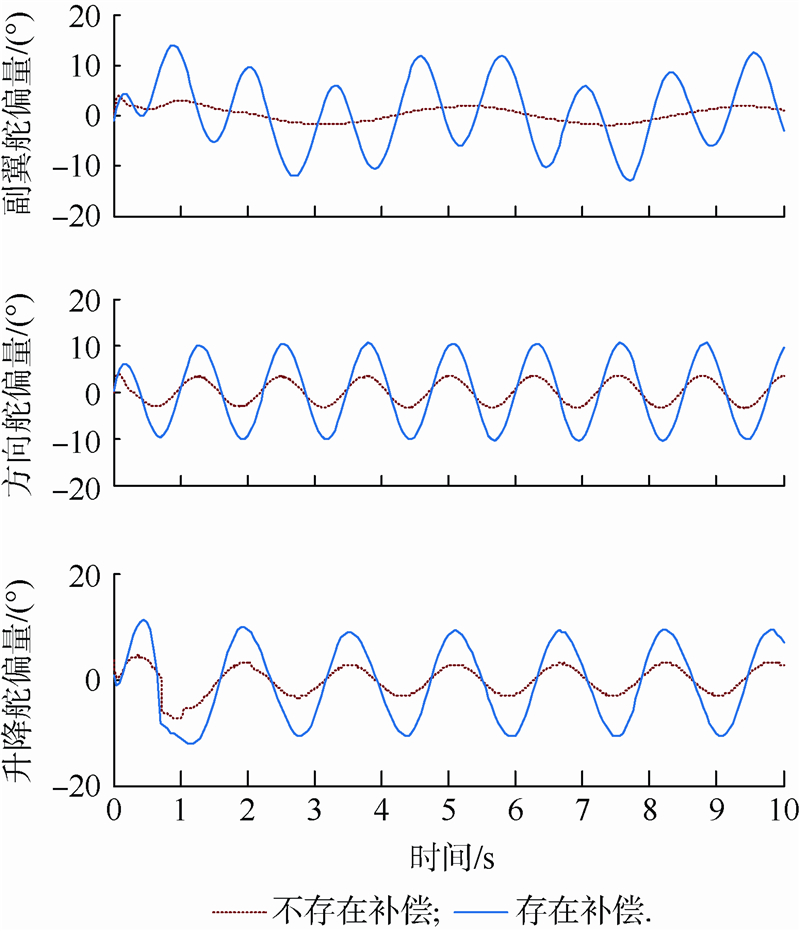| 图 6 存在复合干扰情况下的舵偏角响应曲线Fig. 6 Deflection angle response in the presence of compound disturbances |
上述仿真结果表明,在有外界时变干扰和气动参数大范围摄动的情况下,文献[7]以及本文的方案均能平稳且迅速地跟踪给定的参考指令,但文献[7]不足之处在于:一方面,由于非线性干扰观测器无法快速且精准地对干扰进行重构,导致过渡期间攻角响应超调较大;另一方面,由于文献[7]未采用TD对姿态标称指令安排过渡过程,微分信号的峰值现象无法避免,两种因素综合起来导致飞控系统在初始阶段付出更多的控制量.相反,由于滑模干扰观测器能对复合干扰快速精确地补偿,控制量均在合理约束范围内,整个系统表现出良好的控制性能和鲁棒性,进一步有力证明了本文控制方案的优越性.
6 结 论本文针对高超声速飞行器再入过程强鲁棒、强自适应的姿态控制需求,提出了基于SMDO-TLC的高超声速飞行器复合姿态控制方法.
1) 通过将姿态回路中的伪微分器替换为非线性跟踪微分器,有效改善了低动压飞行条件下的控制品质,避免了执行机构饱和现象的发生,该思路同样适用于执行机构较少且需要获取指令微分信号的控制系统;
2) 借鉴动态滑模控制器的设计思想,设计了二阶滑模干扰观测器,其具有重构误差收敛速度快、重构精度高、抖振效应微弱等优点;
3) 与现有方法相比,本文提出的控制策略能够解决控制约束条件下受扰再入飞行器的姿态跟踪问题,具有更好的暂态特性和静态品质,可以适应高超声速飞行器快时变、高精度以及强鲁棒的控制需求.
| [1] | 黄琳,段志生,杨剑影.近空间高超声速飞行器对控制科学的挑战[J].控制理论与应用,2011,28(10):1496-1505 Huang Lin,Duan Zhisheng,Yang Jianying.Challenges of control science in near space hypersonic aircrafts[J].Control Theory and Applications,2011,28(10):1496-1505(in Chinese) |
| Cited By in Cnki (22) | Click to display the text | |
| [2] | Wang Q,Stengel R F.Robust nonlinear control of a hypersonic aircraft[J].Journal of Guidance,Control and Dynamics,2000,23(4):577-584 |
| Click to display the text | |
| [3] | Xu H J,Ioannou P A.Adaptive sliding mode control design for a hypersonic flight vehicle[J].Journal of Guidance,Control and Dynamics,2004,25(5):829-838 |
| Click to display the text | |
| [4] | Xu H J,Mirmirani M. Robust neural adaptive control of a hypersonic flight vehicle[C]//AIAA Guidance,Navigation and Control Conference and Exhibit.Austin,Texas:AIAA,2003:1-8 |
| Click to display the text | |
| [5] | Zhu J J,Banker D.Hall C E.X-33 ascent flight control design by trajectory linearization-a singular perturbation approach[C]//AIAA Guidance,Navigation and Control Conference and Exhibit.Denver:AIAA,2000:1-19 |
| [6] | Bevacqua T,Best E,Huizenga A.Improved trajectory linearization flight controller for reusable launch vehicles[C]//AIAA Guidance,Navigation and Control Conference and Exhibit.Reno:AIAA,2004:875-887 |
| Click to display the text | |
| [7] | 朱亮,姜长生.基于非线性干扰观测器的空天飞行器轨迹线性化控制[J].南京航空航天大学学报,2007,39(4):490-495 Zhu Liang,Jiang Changsheng.Nonlinear disturbance observer-enhanced trajectory linearization control for aerospace vehicle[J].Journal of Nanjing University of Aeronautics & Astronautics,2007,39(4):490-495(in Chinese) |
| Cited By in Cnki (4) | Click to display the text | |
| [8] | 朱亮,姜长生,陈海通,等.基于单隐层神经网络的空天飞行器直接自适应轨迹线性化控制[J].宇航学报,2006,27(3):338-344 Zhu Liang,Jiang Changsheng,Chen Haitong,et al.Direct TLC for aerospace vehicle using single hidden layer NN[J].Journal of Astronautics,2006,27(3):338-344(in Chinese) |
| Cited By in Cnki (29) | |
| [9] | Lu Y S.Sliding-mode disturbance observer with switching-gain adaptation and its application to optical disk drives[J].IEEE Transactions on Industrial Electronic,2009,56(9):3743-3750 |
| Click to display the text | |
| [10] | Hall C E,Shtessel Y B.Sliding-mode disturbance observer based control for a reusable launch vehicle[J].Journal of Guidance,Control,and Dynamics,2006,29(6):1315-1328 |
| Click to display the text | |
| [11] | Besnard L,Shtessrel Y B,Landrum B.Quadrotor vehicle control via sliding mode controller driven by sliding mode disturbance observer[J].Journal of the Franklin Institute,2012,349(2):658-684 |
| Click to display the text | |
| [12] | Shaughnessy J D,Pinckney S Z,McMinn J D.Hypersonic vehicle simulation model:winged-cone configuration[R].NASA TM-102610,1990 |
| Click to display the text | |
| [13] | Khalil H K.Nonlinear systems[M].3rd ed.Uppe Saddle River,New Jersey:Prentice-Hall,2002 |
| [14] | 陈小庆.高超声速滑翔飞行器机动技术研究[D].长沙:国防科技大学,2011:108-124 Chen Xiaoqing.The key technology relative to the manuverability of hypersonic gliding vehicle[D].Changsha:National University of Defense Technology,2011:108-124(in Chinese) |
| Cited By in Cnki (0) | |
| [15] | Ibrir S.Linear time-derivative trackers[J].Automatica,2004,40(3):397-405 |
| Click to display the text | |
| [16] | 韩京清.自抗扰控制技术[M].北京:国防工业出版社,2008:56-66 Han Jingqing.Active disturbance rejection control technique[M].Beijing:National Defense Industry Press,2008:56-66(in Chinese) |
| [17] | Chen W H.Nonlinear disturbance observer enhanced dynamic inversion control of missiles[J].Journal of Guidance,Control and Dynamics,2003,26(1):161-166 |
| Click to display the text |
