随着现代飞行器气动设计要求的提高,工程界对CFD(Computational Fluid Dynamics)数值模拟的精度提出了更高要求.2009年欧洲ADIGMA项目研究表明[1],当流动较为复杂时,目前广泛使用的二阶格式无法获得满足精度要求的计算结果.而高阶格式由于具有计算精度高、数值耗散低的特点,能够较为精确地刻画流场中的间断,并保证光滑流动区域的计算精度,在流动结构复杂的情况下具有明显优势.因此,高阶格式已成为计算流体力学数值方法的研究趋势[2].
ENO(Essential Non-Oscillatory)格式[3,4,5]作为高阶、高精度格式的典型代表,自1987年提出以来[3]得到了广泛关注,并在此基础上发展了WENO(Weighted-ENO)格式[6,7,8]、CENO(Central-ENO)[9]等多种高阶格式.Huynh[10]基于ENO格式提出一种无振荡高精度格式,以减小ENO格式的耗散性.Suresh和Huynh[11,12]则将该格式扩展到高阶精度.本文研究了这种无振荡格式的三阶格式(Cn3,Centered nonoscillatory scheme of thrid order)在计算精度、激波捕捉等方面的性能,并将其与目前常用的三阶、五阶WENO格式进行对比.重点分析了格式的间断分辨率、计算稳定性和数值耗散等性能,以期对该格式有较为全面的认识,为今后格式构造和应用提供思路.
1 控制方程和离散方法
二维无黏可压欧拉方程可以写成如下形式:
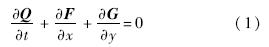
定义单元Iij为
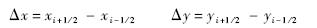
在单元Iij上对式(1)进行积分,得有限体积法的半离散形式方程:
,
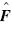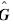为对守恒通量的近似Riemann求解,本文使用Roe格式;QL,QR为单元界面左右两侧的守恒通量,由插值格式获得.除了以下介绍的Cn3格式外,本文还使用了三阶和五阶WENO格式进行对比.2 Cn3格式
为了获得三阶精度的插值格式,需要进行抛物线插值[11].以i方向为例,对于每个网格单元Ii,使用该单元的5个相邻单元进行插值,即[Ii-2,…,Ii+2].令vi为每个单元格心原始变量值,Ri(x)为单元内原始变量的插值函数,给出抛物线插值公式:
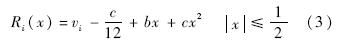
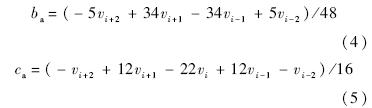
在光滑区域,式(4)、式(5)的参数取值能得到非常精确的计算结果,但在间断区域,这样的插值会出现振荡.为了抑制间断区域的振荡,需要对插值参数加以修正,以同时满足单调性和精度的双重要求[11].
1) 确定单调区域.
根据Harten等人[3]的ENO格式给出分段线性斜率:
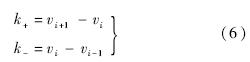
对于单调递增数据,为保持单调性,要求：
对于单调递减数据,将式(7)中的≥改成≤即可.这样就得到了插值所需的单调区域.
2) 确定精确区域.
使用经过(vi-2,vi-1,iv),(vi-1,vi,vi+1),(vi,vi+1,vi+2)的3条抛物线,可以得到3组二次项和三次项系数b和c.将这些系数用下标-,0,+进行区分,得到
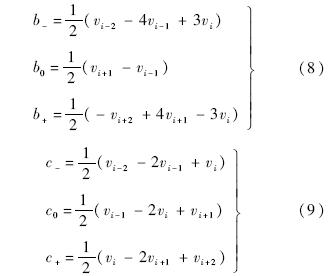
进一步定义:
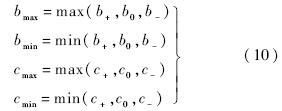
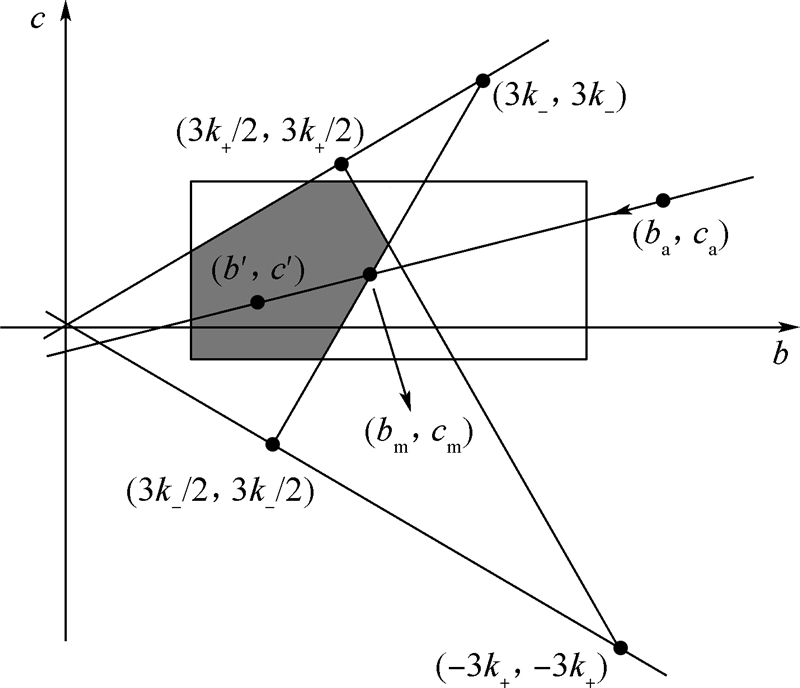
可以证明[11],当插值参数b和c处在单调区域和精确区域的重叠部分时(如图 1),既能抑制数值振荡,又能保证插值公式的精度.
3) 修正ba,ca.
取该重叠区域的一点(b′,c′),使得
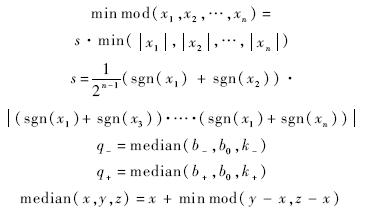
将式(4)和式(5)计算得到的插值参数点(ba,ca)与(b′,c′)相连,所得直线与前述重叠区域将有2个交点,其中处在(ba,ca)和(b′,c′)之间的即为修正后的插值参数(bm,cm)(如图 1,详见文献[11]).将(bm,cm)代入式(3),求得单元界面的原始变量值,进而能够得到守恒变量Q的值.
3 计算结果与分析 3.1 Sod激波管
计算域为[0,1],网格点数为100,初始条件为[13]
计算终止时间为t=0.2.
图 2给出了三阶WENO(weno3)和三阶中心无振荡格式(Cn3)计算结果的无量纲密度关于计算域X∈[0,1]的分布曲线.从图中可以看出,2种格式对间断的分辨率相当.但三阶WENO格式在间断附近出现明显的数值振荡,Cn3格式的结果则较为稳定.
 |
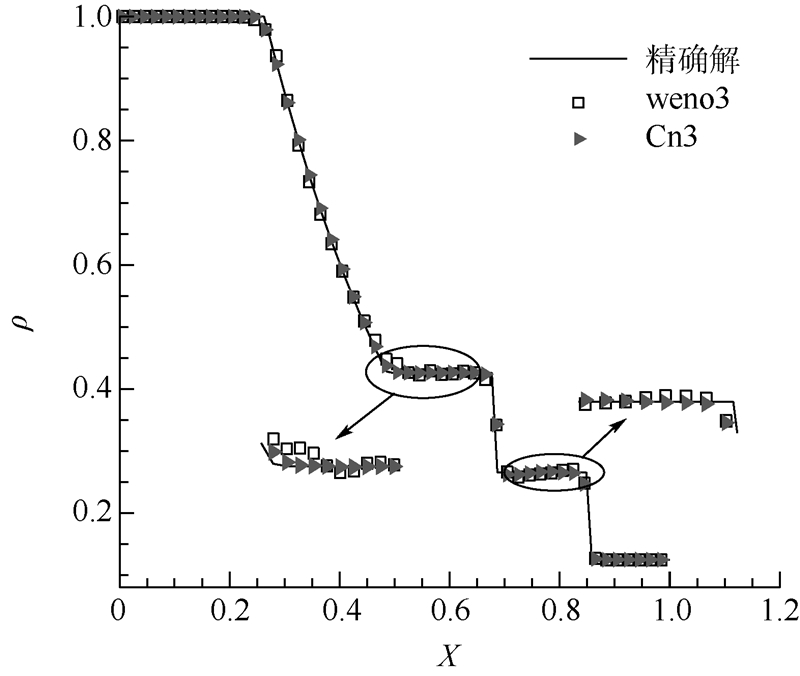| 图 2 Sod问题密度分布曲线Fig. 2 Density distributions of Sod’s problem |
Shu-Osher问题[5]是一维的激波湍流相互干扰问题.在区间[-5,5]中,一道移动的马赫数为3的激波与一道密度正弦波相交,初始流场描述如下:
计算终止时间为t=1.8.使用三阶、五阶WENO格式及Cn3格式进行计算,网格单元数量为400,并采用密网格(网格单元数为1600)的计算结果作为参照(如图 3所示,纵坐标为无量纲密度).
 |
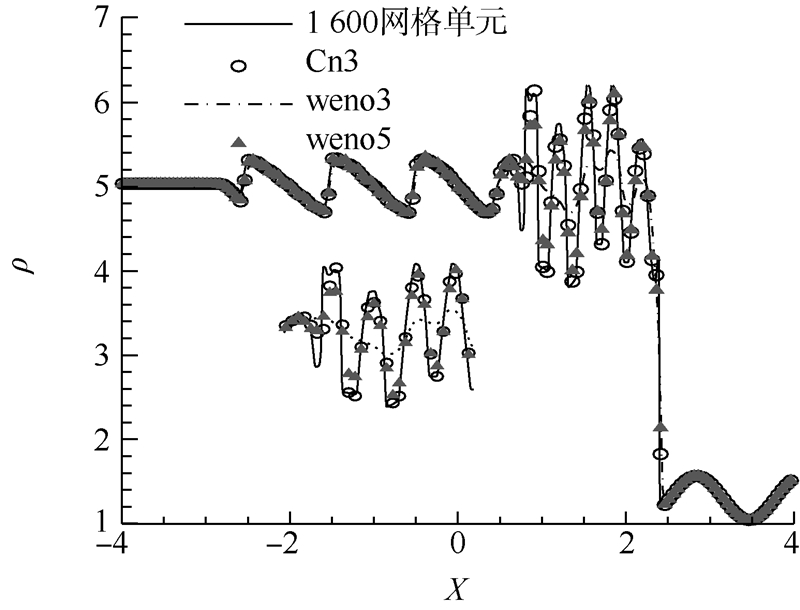| 图 3 Shu-Osher问题密度分布曲线Fig. 3 Density distributions of Shu-Osher’s ploblem |
通过比较发现,在x<0区域(即小激波区域),3种格式对激波的捕捉精度相似,且与密网格的计算结果相近.在x>0区域(即熵波区域),三阶WENO格式会将小尺度流动结构“抹平”;五阶WENO格式虽然能够捕捉到部分小尺度流动结构,但极值点附近的计算精度较低;Cn3格式对该部分流动结构的捕捉精度最高,且与密网格的计算结果较接近.可见,Cn3格式能够在抑制非物理振荡的同时保证对光滑区域流动结构的高精度计算.
3.3 二维周期涡输运
本算例[14]是用来检验格式耗散特性的典型算例.初始流场为在均匀流场上添加了一个等熵涡,该涡的强度为Γ=5,并将随主流向下游输运.计算区域为10×10的方形区域,网格点数为100×100.扰动的形式如下:
 |
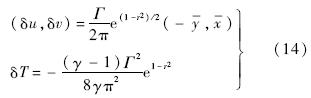
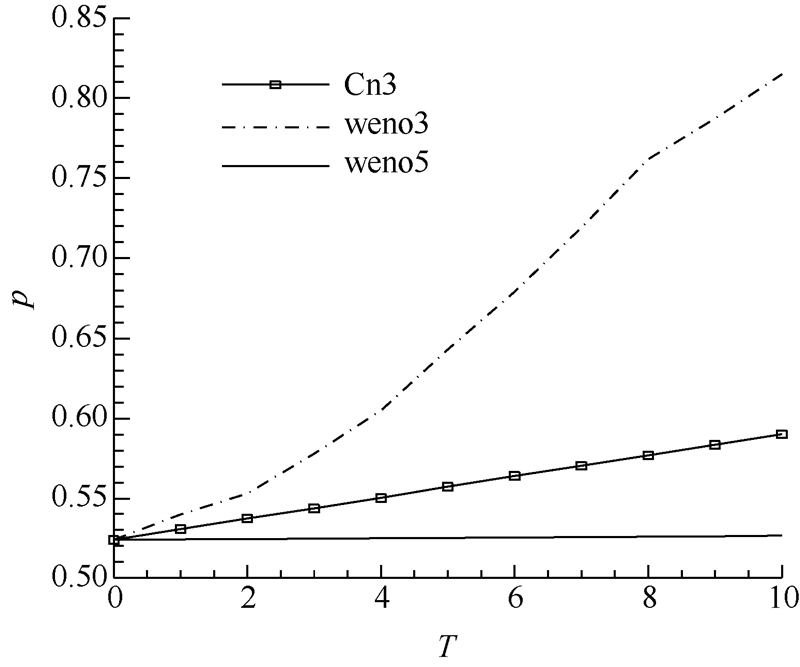| 图 4 涡核压力变化曲线Fig. 4 Variation curves of the vortex’s center |
 |
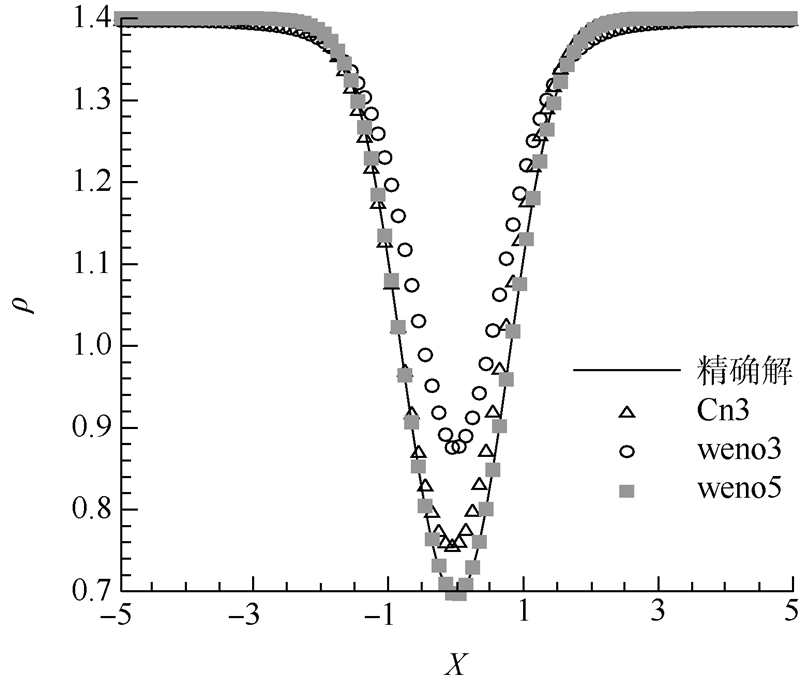| 图 5 涡中心线密度分布曲线Fig. 5 Density distributions along the center-line of the vortex |
该算例[15]求解的是Euler方程,计算域为[0,4]×[0,1],其中下边界[0,1/6]的区域以及左边界均给定激波的波后条件,下边界[1/6,4]的位置为滑移壁面条件,右边界给定出流条件,上边界根据激波每一时刻所处的位置分别给定激波的波前和波后条件.初始时刻,在计算域中给定一个与x轴成60°夹角的马赫数为10的激波,该激波从x=1/6,y=0的位置一直延伸到上边界,并向右侧快速移动.计算时间推进到t=0.2,网格量为480×120.图 6、图 7给出了3种格式计算结果密度等值线.比较看出,Cn3格式能够计算出三叉点出发的滑移线的部分不稳定结构,在壁面喷流结构的捕捉上也较为清晰,这是2种WENO格式都未能计算出来的.可见Cn3格式接触间断的计算分辨率高于2种WENO格式.
 |
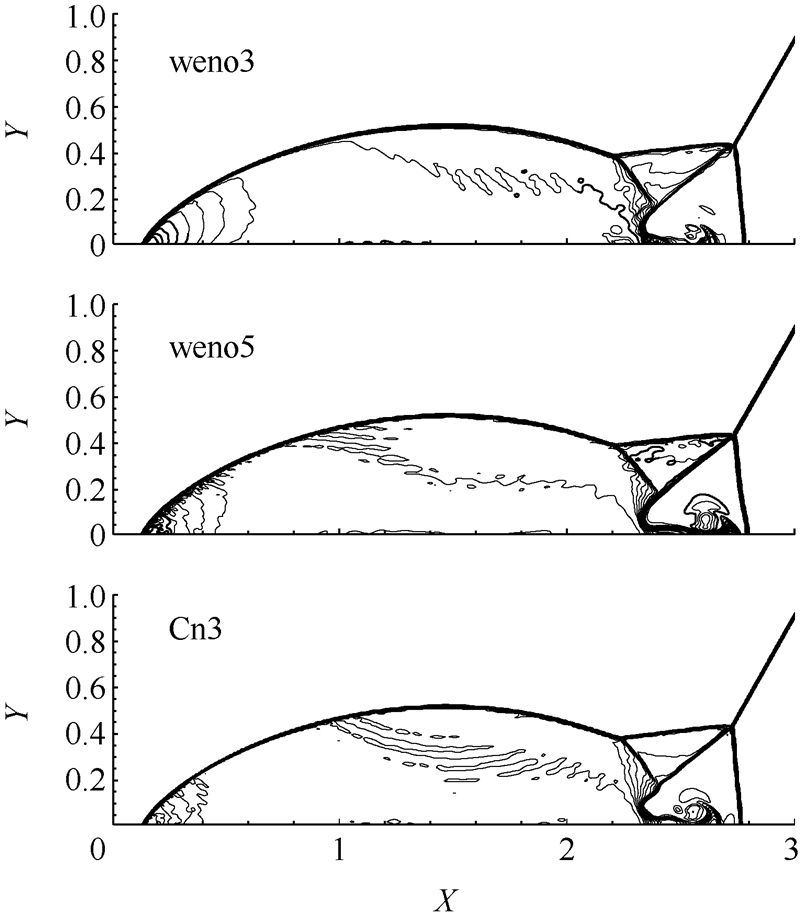| 图 6 双马赫反射密度等值线计算结果Fig. 6 Density contours of double Mach reflection |
 |
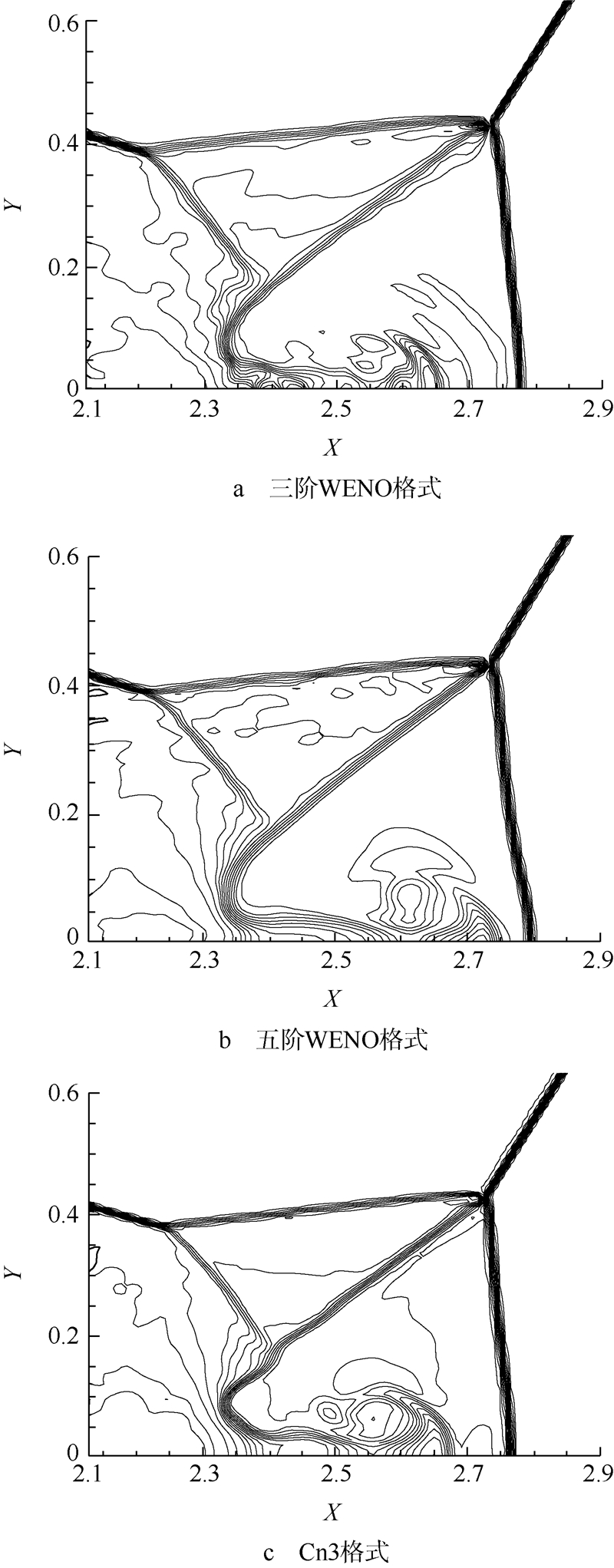| 图 7 双马赫反射密度等值线计算结果细节Fig. 7 Details of density contours of double Mach reflection |
1) 对比三阶WENO格式,Cn3格式能够较好地抑制数值振荡;同时,Cn3格式的数值耗散小于前者;
2) Cn3格式能够保证光滑流动区域的计算精度,对熵波等小尺度流动结构的污染较小;
3) Cn3格式对激波和接触间断的捕捉精度较高,尤其是在双马赫反射算例中,该格式能够捕捉到部分滑移线的不稳定结构,这种对间断的捕捉能力甚至优于五阶WENO格式.
综合上述分析,认为Cn3格式间断分辨率较高、计算稳定性较强、数值耗散较小,具有继续研究和推广应用的价值.
| [1] | Kroll N.ADIGMA-A European project on the development of adaptive higher-order variational methods for aerospace applications[C]//47th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition.Reston,VA:AIAA,2009 |
| Click to display the text | |
| [2] | 阎超,于剑,徐晶磊,等.CFD模拟方法的发展成就与展望[J].力学进展,2011,41(5):562-589 Yan Chao,Yu Jian,Xu Jinglei,et al.On the achievements and prospects of the methods for computational fluid dynamics[J].Advances in Mechanics,2011,41(5):562-589(in Chinese) |
| Cited By in Cnki (44) | |
| [3] | Harten A,Engquist B,Osher S,et al.Uniformly high order accurate essentially non-oscillatory schemes,III[J].Journal of Computational Physics,1987,71(2):231-303 |
| Click to display the text | |
| [4] | Shu C W,Osher S.Efficient implementation of essentially non-oscillatory shock-capturing schemes[J].Journal of Computational Physics,1988,77(2):439-471 |
| Click to display the text | |
| [5] | Osher S,Shu C.Efficient implementation of essentially non-oscillatory shock-capturing schemes,II[J].Journal of Computational Physics,1989,83(1):32-78 |
| Click to display the text | |
| [6] | Liu X D,Osher S,Chan T.Weighted essentially non-oscillatory schemes[J].Journal of Computational Physics,1994,115(1):200-212 |
| Click to display the text | |
| [7] | Jiang G S,Shu C W.Efficient implementation of weighted ENO schemes[J].Journal of Computational Physics,1996,126(1):202-228 |
| Click to display the text | |
| [8] | Shu C W.High order weighted essentially nonoscillatory schemes for convection dominated problems[J].SIAM Review,2009,51(1):82-126 |
| Click to display the text | |
| [9] | Ivan L,Groth C P T.High-order solution-adaptive central essentially non-oscillatory (CENO) method for viscous flows[J].AIAA Paper,2011:2011-367 |
| Click to display the text | |
| [10] | Huynh H T.Accurate upwind schemes for the Euler equations[C]//12th Computational Fluid Dynamics Conference.San Diego,CA:AIAA,1995:1022-1039 |
| Click to display the text | |
| [11] | Suresh A.Centered nonoscillatory schemes of third order[C]//12th Computational Fluid Dynamics Conference.San Diego,CA:AIAA,1995:1292-1305 |
| Click to display the text | |
| [12] | Suresh A,Huynh H T.Accurate monotonicity-preserving schemes with Runge-Kutta time stepping[J].Journal of Computational Physics,1997,136(1):83-99 |
| Click to display the text | |
| [13] | Sod G A.A survey of several finite difference methods for systems of nonlinear hyperbolic conservation laws[J].Journal of Computational Physics,1978,27(1):1-31 |
| Click to display the text | |
| [14] | Nichols R H,Tramel R W,Buning P G.Evaluation of two high-order weighted essentially nonoscillatory schemes[J].AIAA Journal,2008,46(12):3090-3102 |
| Click to display the text | |
| [15] | Woodward P,Colella P.The numerical simulation of two-dimensional fluid flow with strong shocks[J].Journal of Computational Physics,1984,54(1):115-173 |
| Click to display the text |
