Download PDF  
文章快速检索  
  高级检索
引用本文
陈磊, 黄翔, 赵乐乐, 李泷杲. 飞机装配坐标系公共基准点粗差检测与修正方法[J]. 北京航空航天大学学报, 2014, 40(11): 1589-1594
Chen Lei, Huang Xiang, Zhao Lele, Li Shuanggao. Gross error detection and correction method of public reference point in aircraft assembly coordinate system[J]. Journal of Beijing University of Aeronautics and Astronsutics, 2014, 40(11): 1589-1594.
飞机装配坐标系公共基准点粗差检测与修正方法
陈磊, 黄翔, 赵乐乐, 李泷杲    
南京航空航天大学 机电学院, 南京 210016
收稿日期:2013-11-21; 网络出版日期: 2014-03-21
基金项目：国家自然科学基金资助项目(51275234);航空科学基金资助项目(20132252038).
作者简介: 陈磊(1970-),男,上海人,在职博士生,上海飞机制造有限公司研究员,chenlei@comac.cc.
摘要：针对因厂房地基下沉等因素引起的飞机数字化装配体系中公共基准点产生偏差的问题,提出一种飞机装配坐标系公共基准点粗差检测与校正方法.该方法通过泰勒展开布尔沙-沃尔夫空间坐标转换模型形成了适用于大旋转角的坐标系转换线性模型,并结合拟准检定法检测并估算偏差较大的基准点,进而给出了公共基准点在装配全局坐标系下的坐标修正模型.采用激光跟踪仪对公共基准点进行测量并用上述方法修正公共基准点坐标.实验证明,该方法能有效检测粗差并修正,提高飞机装配坐标系的精度.
关键词： 飞机装配     坐标系     泰勒展开     粗差检测     坐标修正    
Gross error detection and correction method of public reference point in aircraft assembly coordinate system
Chen Lei, Huang Xiang, Zhao Lele, Li Shuanggao     
College of Mechanical and Electrical Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China
Abstract:A gross error detection and correction method of the public reference point in an aircraft assembly coordinate system was proposed for such deviations of a public reference point in a digitalized aircraft assembly system as resulted from foundation sinking of a workshop or other factors. In this method, a coordinates transformation linear model applicable to a large rotation angle was built by expanding the Bursa-Wolf coordinates transformation model in Taylor' s expansion, and in combination with the method of quasi-accurate detection (QUAD), the reference point with a relatively large deviation was detected and estimated, and further a coordinates correction model of the public reference point was put forward in a global coordinates for assembly. The public reference point was measured with a laser tracker and then the public reference point coordinates was corrected by the abovementioned method. Experiments prove that the gross error could be effectively detected and corrected by this method, thus the precision of the aircraft assembly coordinate system could be improved.
Key words: aircraft assembly     coordinate system     Taylor expansion     gross error detection     coordinate correction    

现代飞机装配技术以数字化技术为基础,通过构建飞机装配坐标系来精确定位装配工装夹具进而实现飞机零部件的精确装配,尤其是以飞机大部件自动对接为代表的柔性装配技术[1],由于完全采用自动定位控制技术来实现部件对接装配,为保证柔性定位系统的定位协调和精度,对装配坐标系构建的准确性有着更高的要求.

目前通用的装配坐标系构建方法是以数字化测量设备为基础,构建公共基准点阵列,将其测量坐标与全局设计坐标相对应,进而形成与设计模型一致的直观装配环境的方法.公共基准点阵列的布设精度会对最终的装配精度产生重要影响.因此在利用公共基准点构建装配坐标系时,需对公共基准点布设精度进行检测,校正或剔除偏差大的基准点.为此,牛琳等研究了在微小旋转角度下[2],以拟合误差最小为目标的公共基准点选择方法.赵宝峰等研究了坐标转换模型和公共基准点分布对平面坐标系转换精度的影响[3].王建民等运用经典的平差方法结合可靠性理论采用搜索法进行粗差定位[4].Ricardo等研究了一种基于多元线性回归模型的参数校准问题,运用线性最小二乘法解决测量数据中的冗余性及粗差识别问题[5].Gonzalez等提出一种应用于油砂开采过程在线动态贝叶斯粗差检测方法[6].Paolo则基于小波分析研究无先验知识的信号粗差检测问题[7].Amirreza等研究数字地面模型中的数据测量粗差[8].Bretas等运用经典的加权最小二乘方法从几何学的角度研究电力系统状态预估中的粗差检测、识别与修改问题[9].此外这些研究都针对大地测量,适用于小旋转角空间坐标转换及其坐标系精度校正,而飞机装配坐标系之间的转换是大旋转角、空间直角坐标系的坐标系转换,与上述研究有着较大差异,因此上述研究结果不能直接应用于飞机装配.以我国自主研发制造的支线客机ARJ21-700翼身柔性对接装配为例,由于地基沉降、长期振动等原因,公共基准点的空间坐标偏差最高可达0.8~1.0mm,进而不可避免引入误差.长期以来,一直使用对所有的公共基准点进行人工重新测量标定的方法,以消除公共基准点偏移.该方法虽然从一定程度上避免公共基准点偏移,但无差别的重新标定势必使得飞机制造效率和精度都难得到保证.

针对上述问题本文提出一种飞机装配坐标系公共基准点的粗差检测与修正方法,通过建立大旋转角的坐标系转换模型与拟准检定算法,检测公共基准点的测量坐标和理论坐标是否存在测量粗差,进而给出公共基准点坐标修正模型对其进行坐标修正.实际检验证明,此方法能够有效检测出飞机装配坐标系公共基准点粗差并予以一定程度的校正.

1 坐标系转换模型线性化

通过公共基准点测量坐标与理论坐标的映射,将测量坐标转换到全局设计坐标系,所形成的坐标转换为非线性模型(式(1)),为使得后续粗差检测方便,利用泰勒级数展开将坐标转换模型转换成线性模型.

构建基于布尔沙-沃尔夫(Bursa-Wolf)模型的坐标转换模型[10]:记空间任一公共基准点pi在测量坐标系和全局坐标系中的坐标分别为

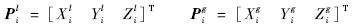
测量坐标系原点在全局坐标系中的坐标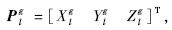测量坐标系相对于全局设计坐标系的旋转参数分别为εx,εy,εz,尺度缩放因子为k,则有坐标转换模型:

式中

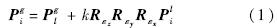
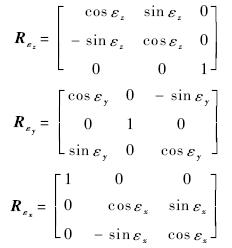
为方便描述,记旋转矩阵Rgl:

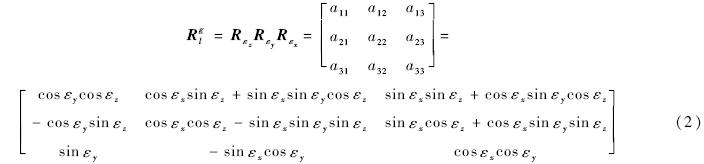
布尔沙模型对旋转参数的三角函数做了近似处理,仅适用于旋转角是微小角度的情况,无法用于飞机装配坐标系构建过程中大旋转坐标的转换.为此本文将Rgl中的9个方向余弦都作为未知参数,以适用于任意旋转角的坐标系转换.此外,由于三维直角坐标转换为正交变换,因此9个方

向余弦满足正交条件[11],即9个未知参数仅3个独立变量.将Rgl代入式(1),对其进行泰勒展开,省略二阶以上分量得:

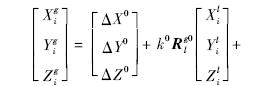
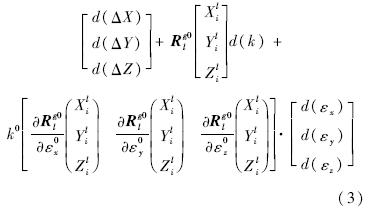
式中,上标为0的表示取近似值,d(ΔX),d(ΔY),d(ΔZ),d(k),d(εx),d(εy),d(εz)为坐标系转换参数的改正数,其中d(ΔX),d(ΔY),d(ΔZ)为测量坐标系原点在全局坐标系中的坐标分量偏差.

记:

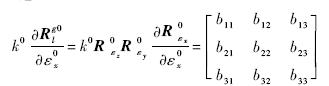
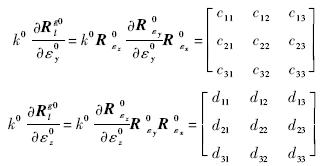
式(3)忽略高阶小量可获得坐标系转换线性化模型:

其中,Bi为坐标系转换系数矩阵;Li为布设误差：

考虑到布设误差,将式(4)写成误差方程的形式:

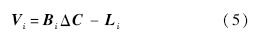
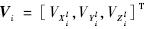式中,表示第i个公共基准点pi布设误差Li的观测值.记n个公共基准点的测量坐标矩阵:

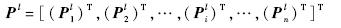
全局理论坐标矩阵:

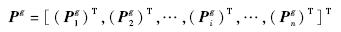
拟合误差矩阵:

坐标系转换系数矩阵:

将式(5)扩展得到拟合误差的观测残差:

利用间接平差原理[12]求解式(6),即可解算出坐标系转换参数的改正数ΔC:

式中W是基准点的观测权重矩阵.

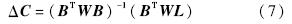
解算出的参数改正数与上次的坐标系转换参数近似值相加作为下次解算用到的参数近似值,如此循环迭代,直至d(ΔX),d(ΔY),d(ΔZ),d(k)小于10-5,d(εx),d(εy),d(εz)小于10-7,将最终的近似值作为转换参数[13].

2 粗差检测与修正

设共选用n个公共基准点构建全局坐标系,由式(6)得到线性观测方程:

式(8)的估值形式为

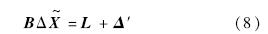
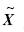式(8)、式(9)中,Δ为ΔX的估值;Δ′为拟合误差的真误差.

记观测值的平差因子为J,则有

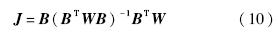
利用式(10)可较易证明:JB=B,此处省略证明过程.利用JB=B,可得

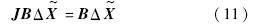
联立式(8)和式(11),可得

化简式(12),可得

式中I为单位矩阵.

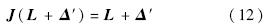
记R′=I-J,将R′=I-J代入式(13),可推导出拟合误差的真误差与拟合误差的观测值的关系式:

记拟准测量值的真误差为Δr,坐标系转换系数矩阵为Br,附加的约束方程组的系数矩阵GQ=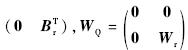.综合GQ和WQ的表达式和式(14),可得

利用R′=I-J和JB=B,可较易证明R′B=0.利用R′B=0,可计算得R′GQ=0.由附加约束条件法解算秩亏线性方程可知,如果GQ满足R′GQ=0,则由此解算得到的误差估值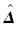是式(15)的加权最小范数解.

进一步推导式(15),可得

利用式(16)可得

利用式(17),得

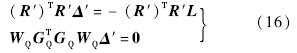
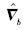假设根据判断条件认定观测值中含有b个粗差,可得到b个3n×1维的向量ej=[0,…,0,1,0,…,0]T,ej表示第j个观测值含有粗差.记Eb=[e1，e2，…，eb],设粗差估值为,则含有粗差的观测方程为

式中N为分离了粗差的真值向量.利用最小二乘法,可求出粗差估值:

由式(20)可得协因数矩阵为

利用式(21),可得公共基准点拟合误差的修正计算式：

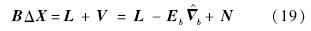
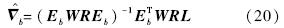
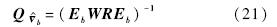
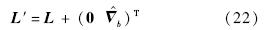
因为与布设误差相比,激光跟踪仪测量误差高阶小量,所以应对布设误差进行修正.利用式(22),可得公共基准点在测量坐标系下的修正坐标为

利用坐标变换,公共基准点在装配全局坐标系下的修正坐标为

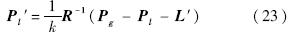
坐标修正后,坐标系转换参数的改正的估值为

式中B是3n×7的矩阵.

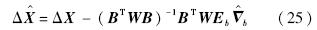
假设最终确定了观测值中含有b个粗差,可得到b个n维单位向量ej=(0,…,0,1,0,…，0)T,对应第j个观测值有粗差,即第j个分量为1,其余为0,令Cb=(e1,e2,…,eb).利用粗差的拟准检定法[14,15,16],即含有粗差的公共基准点的布设误差修正值为

由式(9),公共基准点的布设误差L的修正结果为

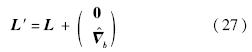
由式(4),可得公共基准点的测量坐标系下的修正坐标:

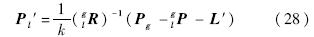
对多次测量结果均含有粗差的公共基准点,公共基准点在装配全局坐标系下的修正坐标为

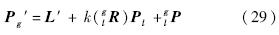
3 应用分析

本文利用Leica AT901-B激光跟踪仪完成ARJ21-700右机翼和中机身的对接装配.利用表 1中的8个公共基准点建立激光跟踪仪测量坐标系与全局设计坐标系之间的转换关系,公共基准点的测量坐标和全局理论坐标如表 1所示.

表 1 公共基准点测量坐标和全局理论坐标 Table 1 Measurement and global theory coordinate marks of public datum points
mm
公共基准点测量坐标全局理论坐标
XYZXYZ
ERS183232.724811589.2308-1509.0511-1796.776322703.6194-2769.4782
ERS27-3604.26214273.6995-1482.4198-4689.263413118.6141-2778.7923
ERS31-3003.32308393.8849-1507.6824-5973.772417078.9115-2775.3322
ERS37-6835.159913079.5816-1557.8352-11483.475019584.3944-2780.5446
ERS431597.11772011.9014-1054.2638977.734213390.1892-2381.2093
ERS53211.91703538.40521612.3583-924.792414131.3982299.9791
TB1-1000.8758-1046.7569-1385.749409500.0000-2728.3635
TB4-3964.87069894.3803-1474.5040-7499.918317998.4181-2728.3783
表选项

利用粗差检测方法,检测上述数据发现基准点ERS31含[0.1808,0.0011,0.1395]T的粗差,基准点ERS43含有[0.0004,0.1701,0.0012]T的粗差,其他基准点不含粗差.对基准点ERS31和ERS43的测量坐标进行修正,计算坐标系转换参数.修正前后坐标系转换参数如表 2所示.

表 2 修正前后坐标系转换参数Table 2 Coordinate transformation parameters before and after correction
转换参数修正前修正后
ΔX/mm-8129.51672843-8129.50643786
ΔY/mm11473.2372768411473.23395897
ΔZ/mm-1394.29425468-1394.31038105
εx/rad-0.00831567-0.00822497
εy/rad0.001472470.00146373
εz/rad-0.45903455-0.45852335
k1.000052381.00002009

表选项

坐标系转换参数微小的变化,在坐标系转换之后可能会带来不容忽视的误差.利用装配空间内,选择若干个没有用于构建转换关系的公共基准点对飞机装配坐标系进行检验验证.选择3个公共基准点ERS20,ERS35,TB7,根据修正前后的坐标系转换参数计算全局位置坐标.坐标系修正前后,3点X,Y,Z各向计算坐标与理论坐标的偏差的绝对值如图 1所示.

图 1 修正前后基准点各向偏差Fig. 1 Deviation of the datum points before and after correction
图选项

从图 1中可以看出,粗差修正前,基准点ERS35的Z方向坐标偏差达到0.23mm,这在飞机大部件装配中是不容忽视的.剔除粗差后,经过修正的坐标系,将基准点ERS35Z方向的偏差由0.23mm降至0.067mm,满足飞机装配公共基准点测量精度要求.该实验说明,粗差检测有效提高了飞机装配坐标系的精度,在飞机装配测量中是必不可少的重要过程.

4 结 论

1) 飞机装配数字化过程中,测量数据转换采用布尔沙-沃尔夫七参数空间坐标转换模型,利用泰勒级数展开将坐标转换模型转换成线性模型.

2) 利用拟准检定法(QUAD)对公共基准点测量数据进行粗差检测,得到公共基准点在装配全局坐标系下的修正坐标公式和坐标系转换参数的改正的估值.

3) 采用Leica激光跟踪仪测量ARJ 21-700右机翼和中机身的对接装配公共基准点坐标,利用本文方法计算粗差估值,对测量数据进行修正.结果表明:基准点偏差最大由0.23mm降至0.067mm,有效提高了飞机装配公共基准点测量精度.

参考文献
[1] 梅中义,朱三山,杨鹏.飞机数字化柔性装配中的数字测量技术[J].航空制造技术,2011(17):44-49 Mei Zhongyi,Zhu Sanshan,Yang Peng.The digital measurement technology of flexible assembly of plane[J].Aeronautical Manufacturing Technology,2011(17):44-49(in Chinese)
Cited By in Cnki (4)
[2] 牛琳,陈建平,田毅.三维坐标转换的公共点选择方法[J].北京测绘,2007(4):9-11 Niu Lin,Chen Jianping,Tian Yi.The selection method of three-dimensional coordinate conversion common point[J].Beijing Surveying and Mapping,2007(4):9-11(in Chinese)
Cited By in Cnki (16)
[3] 赵宝锋,张雪,蒋廷臣.坐标转换模型及公共点选取对转换成果精度的影响[J].淮海工学院学报:自然科学版,2009(4):54-56 Zhao Baofeng,Zhang Xue,Jiang Tingchen.Coordinate transformation model and the common point selection effects on transformation precision[J].Journal of Huaihai Institute of Technology:Natural Science,2009(4):54-56(in Chinese)
Cited By in Cnki (8)
[4] 王建民,张锦,苏巧梅.观测数据中的粗差定位与定值算法[J].武汉大学学报:信息科学版,2013,38(10):1225-1228 Wang Jianmin,Zhang Jin,Su Qiaomei.Algorithm for location and evaluation of gross errors in surveying data[J].Journal of Wuhan University:Information Science,2013,38(10):1225-1228(in Chinese)
Cited By in Cnki
[5] Maronna R,Arcas J.Reconciliation and gross error diagnosis based on regression[J].Computers and Chemical Engineering,2009,33(1):65-71
Click to display the text
[6] Gonzalez R,Huang B,Xu F W,et al.Dynamic bayesian approach to gross error detection and compensation with application toward an oil sands process[J].Chemical Engineering Science,2012(67):44-56
Click to display the text
[7] Paolo M.A wavelet based algorithm without a priori knowledge of noise level for gross errors detection[J].International Conference on Advances in Intelligent Systems,2014:7-12
[8] Amirreza S,Hossein A,Michael S,et al.Statistically robust detection and evaluation of errors in DTMs[C]//2011-Joint Urban Remote Sensing Event.Munich:IEEE,2011:305-308
Click to display the text
[9] Bretas N G,Piereti S A,Bretas A S,et al.A geometrical view for multiple gross errors detection,identification,and correction in power system state estimation[J].IEEE Transactions on Power Systems,2013,28(3):2128-2135
Click to display the text
[10] Kutoglu H S.A comparison of two well known models for 7-parameter transformation[J].The Australian Surveyor,2001,47(1):24-30
Click to display the text
[11] 刘东明,郭际明,施展,等.大角度三维基准转换及公共点的确定[J].测绘通报,2010(1):11-14 Liu Dongming,Guo Jiming,Shi Zhan,et al.Large angle determination of 3D datum transformation and common point[J].Bulletin of Surveying and Mapping,2010(1):11-14(in Chinese)
Click to display the text
[12] 王穗辉.误差理论和测量平差[M].上海:同济大学出版社,2010 Wang Suihui.The error theory and measuring adjustment[M].Shanghai:Tongji University Press,2010(in Chinese)
[13] Li H,Zhong C,Zhi Z.A comprehensive quality evaluation system for coordinate transformation[C]//Proceedings-2nd International Symposium on Data,Privacy,and E-Commerce.Piscataway,NJ:IEEE Computer Society,2010(8):15-20
Click to display the text
[14] 欧吉坤.粗差的拟准检定法(QUAD法)[J].测绘通报,1999(1):15-19 Ou Jikun.The quasi accurate detection method of gross error[J].Bulletin of Surveying and Mapping,1999(1):15-19(in Chinese)
Cited By in Cnki (109)
[15] 欧吉坤.再论拟准检定法的原理、实施与应用[J].测绘工程,2002,11(4):3-6 Ou Jikun.Futher on the principle,implementation and application of the quasi accurate detection method[J].Engineering of Surveying and Mapping,2002,11(4):3-6(in Chinese)
Cited By in Cnki (10)
[16] 柴艳菊,欧吉坤,卢秀山.用MATLAB语言实现粗差的拟准检定法[J].山东科技大学学报:自然科学版,2000,19(3):34-38 Chai Yanju,Ou Jikun,Lu Xiushan.Using MATLAB language to achieve gross error verification[J].Journal of Shandong University of Technology:Natural Science,2000,19(3):34-38(in Chinese)
Cited By in Cnki (3)
http://dx.doi.org/10.13700/j.bh.1001-5965.2013.0672
北京航空航天大学主办。
0

文章信息

陈磊, 黄翔, 赵乐乐, 李泷杲
Chen Lei, Huang Xiang, Zhao Lele, Li Shuanggao
飞机装配坐标系公共基准点粗差检测与修正方法
Gross error detection and correction method of public reference point in aircraft assembly coordinate system
北京航空航天大学学报, 2014, 40(11): 1589-1594
Journal of Beijing University of Aeronautics and Astronsutics, 2014, 40(11): 1589-1594.
http://dx.doi.org/10.13700/j.bh.1001-5965.2013.0672

文章历史

收稿日期：2013-11-21
网络出版日期: 2014-03-21

相关文章

工作空间