2. 北京宇航系统工程研究所, 北京 100076;
3. 北京航空航天大学 飞行器控制一体化技术重点实验室, 北京 100191;
4. 北京航空航天大学 航空科学与工程学院, 北京100191
2. Beijing Astronautics Systems Engineering Institute, Beijing 100076, China;
3. Science and Technology on Aircraft Control Laboratory, Beijing University of Aeronautics and Astronautics, Beijing 100191, China;
4. School of Aeronautic Science and Engineering, Beijing University of Aeronautics and Astronautics, Beijing 100191, China
目前,针对非线性高超声速飞行器动力学模型的控制系统设计,国内外文献主要采用反馈线性化[1,2]、滑模控制[3,4,5,6]、反步法[7,8,9]等实现.反馈线性化的主要缺点在于要求系统参数准确可知,当实际系统参数与名义系统存在较大差别时,闭环性能严重下降,因此鲁棒性不强[10].滑模控制一般与反馈线性化或反步法结合使用.为了避免复杂的虚拟控制变量求导,在反步法中引入了指令滤波器,继而产生了动态面控制方法.在存在不确定项的情况下,动态面控制一般与自适应控制结合使用,即自适应动态面控制.传统的自适应动态面控制通过自适应参数更新律消除Lyapunov函数导数中不确定项估计误差带来的影响,从而保证闭环系统的全局稳定性和跟踪误差的有界性.
传统自适应参数更新律依赖于状态的跟踪误差,估计器与被控对象之间存在很强的耦合,因此将对控制器与估计律参数设计带来很大困难,一个较大的更新律增益并不一定能带来系统性能的改善.目前,一种基于不变流形原理的自适应估计方法得到了广泛研究[11,12,13,14].文献[12]将该方法应用于未知状态的估计.文献[13]将该方法应用到存在未知参数的导弹自动驾驶仪设计.采用该自适应估计方法可以使未知参数估计误差收敛到一个不变流形上,且参数估计器和控制器分离,不存在耦合关系,因此是对传统等价自适应方法的改进.
本文将基于不变流形的估计方法引入到存在未知参数的动态面控制方法中,并将该方法应用到高超声速飞行器的控制上.本文在理论上证明了该方法使闭环系统有界稳定,且跟踪误差能够收敛到原点附近的邻域,并可以通过参数选取保证该邻域足够小.仿真表明本文所提控制方案具有良好的控制效果,实现了存在未知参数情况下的高超声速飞行器跟踪控制,且在未知参数估计上优于传统自适应方法.
1 高超声速飞行器动力学模型
本文采用文献[1]中给出的高超声速飞行器动力学模型,并对该模型作以下假设:
假设1 推力项Tsinα远小于升力L;在升力L中,忽略控制舵偏δe对其的影响.
假设2 忽略推力T对俯仰力矩M的影响.
假设3 认为质心运动方程中力系数不确定性对飞行器运动影响较小,仅考虑绕质心转动方程中力矩系数的不确定性.
将高超声速飞行器动力学模型分成弹道倾角子系统和速度子系统,分别实现对弹道倾角指令和速度指令的跟踪.
针对弹道倾角子系统,定义状态变量:
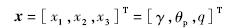
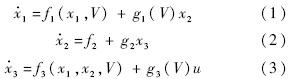
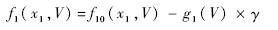
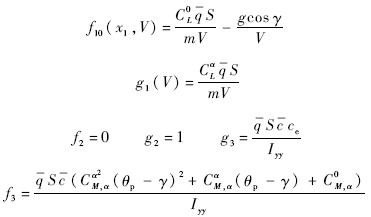
针对速度子系统,建立模型如下：
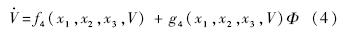
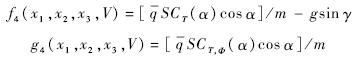
2 弹道倾角子系统控制设计
在第1节中,通过适当假设将整个系统的设计分为弹道倾角子系统和速度子系统,本节采用基于不变流形的自适应动态面控制方法进行弹道倾角子系统的控制设计.
基于不变流形的自适应动态面控制具有模块化的结构,由未知参数估计模块和控制模块两部分组成,两部分的设计过程相互分离.与传统的自适应估计方法不同,估计模块提供的未知参数估计值由两部分之和构成,一部分是由未知参数估计更新律提供的值,另外一部分为设计者给定的已知函数.该估计器设计保证了未知参数估计误差收敛到已知的不变流形上,继而保证了闭环控制系统对参考指令的跟踪效果.
下面首先进行未知参数估计器设计.式(1)~式(3)给出了严反馈形式的弹道倾角子系统模型,根据假设3,式(3)中f3,g3为未知函数,将其表达为以下形式:
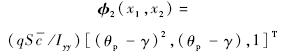
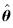为θ的估计值,定义估计误差z=[zT2,z3]T为
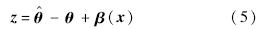
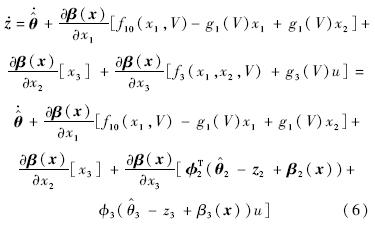
由以上估计误差的导数,选择未知参数自适应更新律为
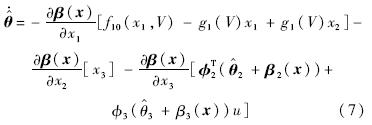
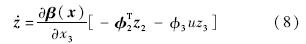
通过选取非线性函数β2(x),β3(x)保证上述误差方程的稳定.选择满足如下偏导数关系的非线性函数：
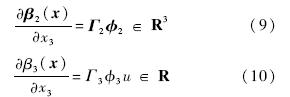
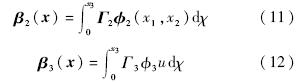
定义Γ=diag{Γ2,Γ3}∈R4,Ψ=[-φT2,-φ3u]T,并将式(9)~式(10)代入误差方程中,得到误差方程为
为了验证估计器误差动力学方程的稳定性,定义正定Lyapunov函数:
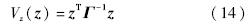
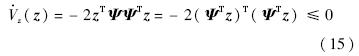
从而z(t)∈L∞,误差系统全局一致稳定.给出以下引理.
引理1[15] (Barbalat引理)设连续可微函数V(x,t):Rn×[0,∞)→R存在下界,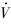
(x,t)≤0,并且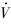(x,t)在［0,∞)是一致连续的,则可以得到结论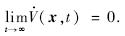
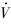z(z)是半负定的,Vz(z)≥0,且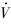z(z)在［0,∞)的全部时间区间上是一致连续的,从而由引理1可得
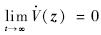,则
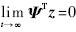.从上面的分析可以看出ΨTz=0是一个不变流形.
在未知参数估计器设计完成后,按如下步骤完成弹道倾角子回路动态面控制器的设计.
步骤1 定义跟踪误差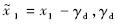
为弹道倾角的指令信号,由方程(1)得
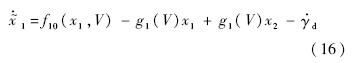
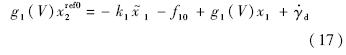
为了避免对解析模型的依赖,采用如下一阶指令滤波器实现对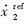
的计算:
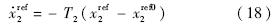
步骤2 定义跟踪误差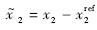
,由方程(2)得
以x3作为虚拟控制变量,选择该步名义虚拟控制值xref03满足如下等式:
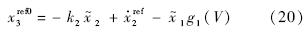
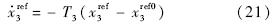
步骤3 定义跟踪误差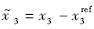
,由方程(3)得
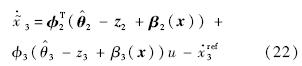
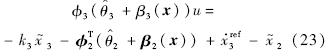
在进行稳定性证明之前,先对指令滤波器带来的影响进行分析.定义指令滤波器带来的参考指令改变为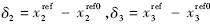
.将x2=
分别代入式(16)、式(19)及式(22)得到
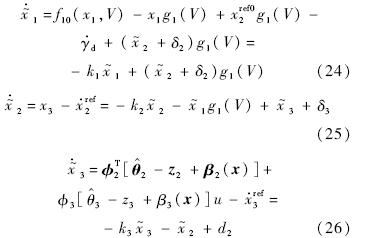
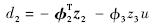由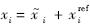
(i=2,3)可以得到
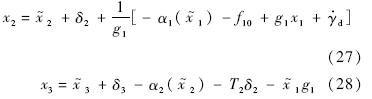
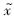1的定义及式(27)和式(28)可以得到
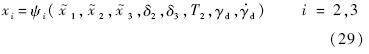
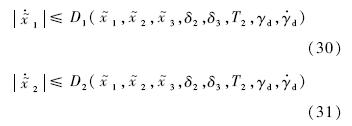
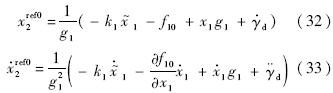
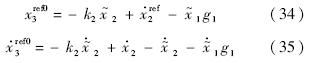
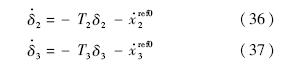
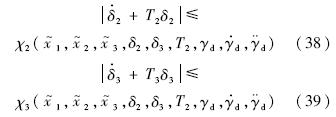
以下分析闭环系统的稳定性.
定理1 对于存在未知参数的弹道倾角子系统式(1)~式(3),在虚拟控制量式(17)、式(20)和实际控制输入式(23),以及未知参数更新律式(7)下,闭环系统对参考指令的跟踪误差有界稳定.
证明 定义Lyapunov函数为
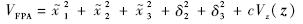
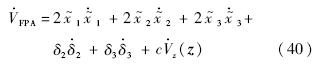
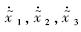的方程代入式(40),得到
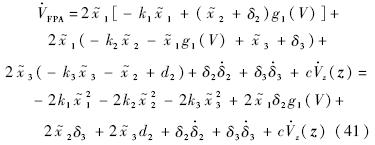
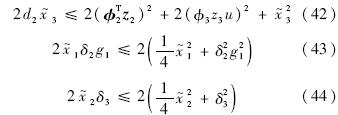
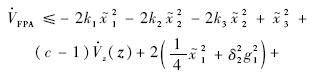
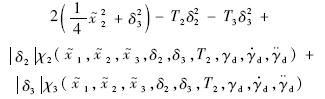
考虑集合
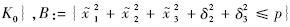,A和B分别为R3和R5上的一个紧集,因此A×B是R8上的一个紧集,因此在A×B上χi(i=2,3)存在一个最大值Mχi.由Young不等式可以得到
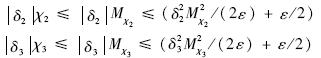
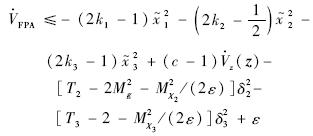
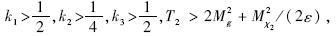
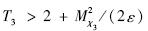,则可得到
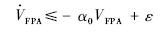
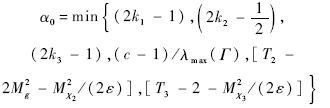
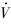FPA≤-α0VFPA+ε,选择合理的控制增益和指令滤波器时间常数,能保证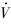FPA≤0,从而A×B的边界为一个不变集,因此闭环系统有界稳定.证毕3 速度子系统控制设计
采用动态逆控制的方法设计速度子系统控制器.定义跟踪误差zV=V-Vd,对其进行求导并将推力T的表达式代入可得
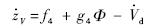
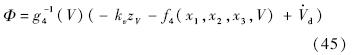
可以证明该控制律保证了速度子系统的稳定性.
4 仿真验证
为了验证上述基于不变流形的自适应动态面控制器的效果,采用文献[1]中的非线性模型进行仿真分析.飞行器跟踪方波变化的弹道倾角信号同时保持速度不变.
飞行器在速度保持不变的情况下,实现高度两次爬升.两次阶跃指令经过两个频率为0.3,阻尼为0.95的二阶环节转化为提供给控制系统的高度指令信号.通过下式将高度指令信号转化为弹道倾角指令信号:
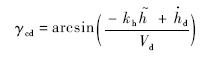
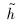为转化为该弹道倾角指令下的高度误差;kh为增益,选择为kh=0.8.采用本文提出的基于不变流形方法实现对弹道倾角指令的跟踪.飞行器初始条件选择为V0=2347.6m,h0=25908m,γ0=0°.弹道倾角子系统3个增益系数分别为k1=1,k2=1,k3=6.速度通道的增益系数为kv=0.8.指令滤波器时间常数为T2=T3=20.选取未知参数的初值为θ20=[5,2,0.16]T,θ30=0.5,自适应参数估计增益选择为Γ2=diag(7,7,7),Γ3=20.为了验证本文提出方法的优势,进行与传统自适应方法的对比,选择传统自适应估计更新律为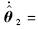
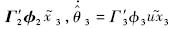,增益选择为Γ′2=Γ2,Γ′3=Γ3.在俯仰角速率方程中前100s加入1°附加攻角的力矩,得到仿真结果如图 1~图 6所示.
 |
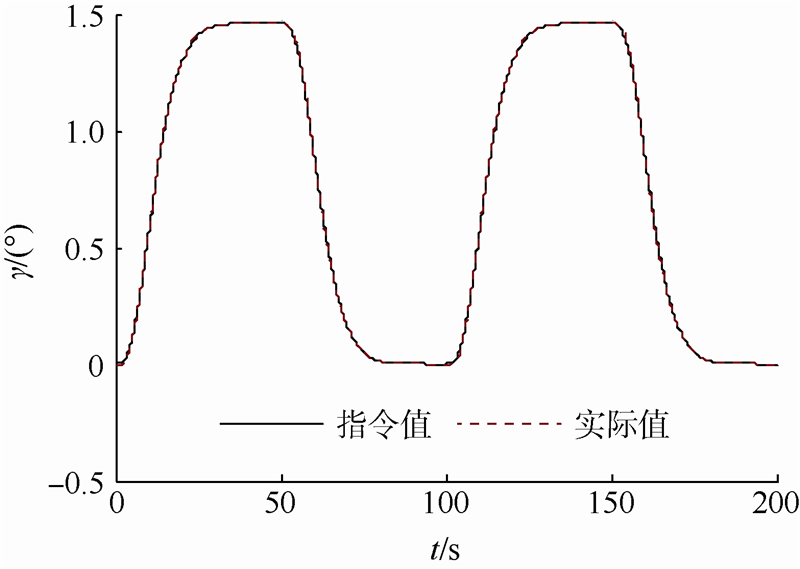| 图 1 弹道倾角跟踪曲线Fig. 1 Tracking curve of flight-path angle |
 |
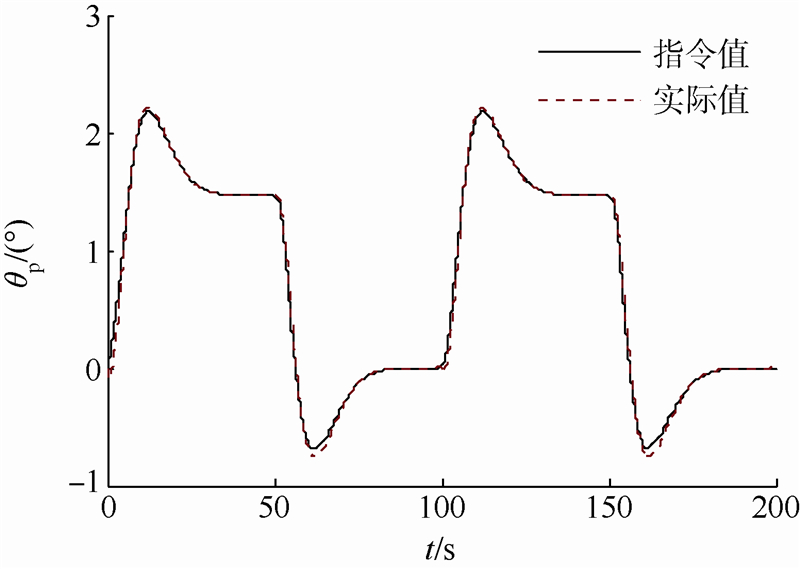| 图 2 俯仰角跟踪曲线Fig. 2 Tracking curve of pitch angle |
 |
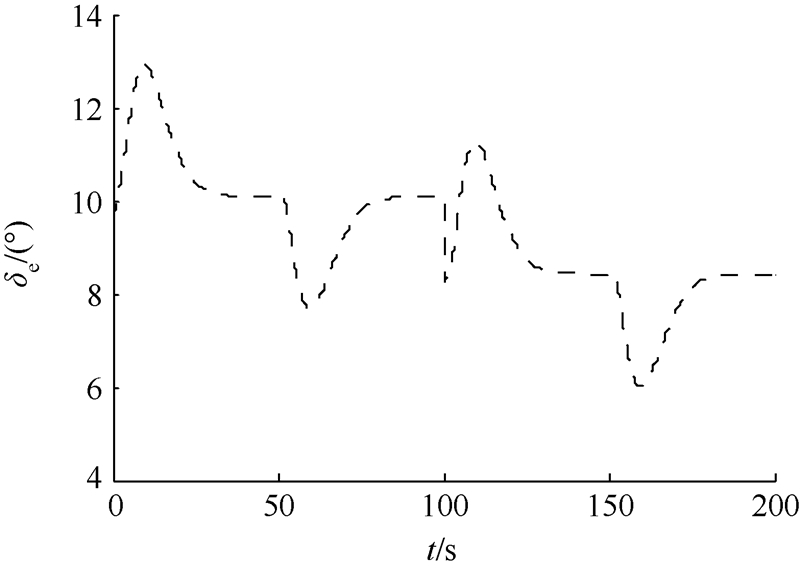| 图 3 舵偏角曲线Fig. 3 Tracking curve of deflection angle |
 |
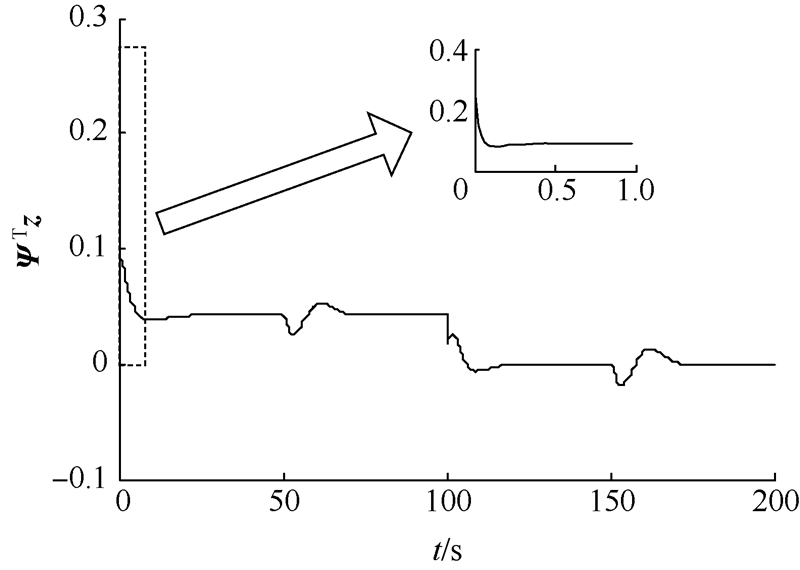| 图 4 ΨTz曲线Fig. 4 Curve of ΨTz |
 |
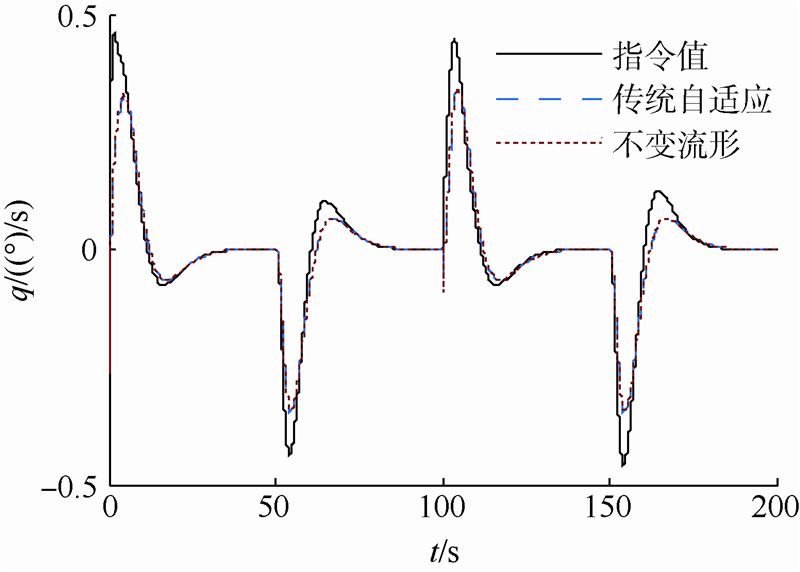| 图 5 俯仰角速率跟踪曲线Fig. 5 Tracking curve of pitch rate |
 |
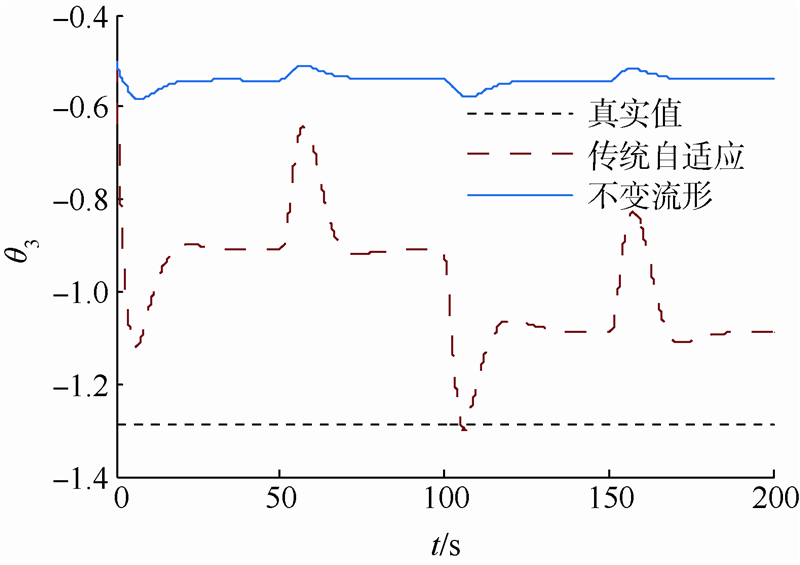| 图 6 θ3估计曲线Fig. 6 Evaluation curve of θ3 |
图 1给出了弹道倾角曲线的跟踪效果,从参考指令信号和跟踪曲线的对比上看,在初始时刻跟踪曲线存在一定的误差,但很快闭环系统实现对参考指令信号的精确跟踪.初始的跟踪误差也可以从图 2给出俯仰角指令的跟踪曲线看出.
图 3给出了舵偏角曲线,其值在合理的范围内.图 4给出了不变流形自适应估计方法中的ΨTz曲线,从曲线可以看出,ΨTz从0.25开始收敛到一个较小的值,但不为0,在100s以后,干扰消失,ΨTz收敛到0,这与理论证明的结论相符.
图 5给出了基于不变流形的自适应动态面方法和传统自适应动态面方法的q跟踪值对比曲线,图 6给出了两者θ3估计值的对比曲线,从对比曲线可以看出,本文提出的方法在参数估计上存在显著优势,在相同干扰条件和相同增益下θ3收敛到较小的误差范围内,而传统自适应方法的估计误差较大.另外,由于本文提出的方法中,参数估计器与控制器分离,因此,参数估计器的增益还可提高,且不必和控制器增益系数协同设计.仿真结果验证了本文所提方法的良好性能.
5 结 论
1) 不确定等价自适应反步控制相比于传统确定等价自适应方法在参数估计上具有显著优势,且由于估计器与控制器设计分离,不需要协同设计,因此参数设计更加容易;
2) 闭环系统的稳定性对控制器增益以及指令滤波器的时间常数提出了要求;
3) 仿真结果表明闭环系统对参考指令具有良好的跟踪效果,参数估计更加准确,验证了本文所提控制方案的有效性.
| [1] | Parker J T,Serrani A,Yurkovich S,et al.Control-oriented modeling of an air-breathing hypersonic vehicle[J].Journal of Guidance,Control,and Dynamics,2007,30(3):856-869 |
| Click to display the text | |
| [2] | 李惠峰,李昭莹.高超声速巡航飞行器在线自适应反馈控制设计[J].北京航空航天大学学报,2010,36(11):1382-1386 Li Huifeng,Li Zhaoying.Adaptive feedback control design for hypersonic cruise flight vehicle[J].Journal of Beijing University of Aeronautics and Astronautics,2010,36(11):1382-1386(in Chinese) |
| Cited By in Cnki (4) | |
| [3] | Xu H J,Mirmirani M D,Ioannou P A.Adaptive sliding mode control design for a hypersonic[J].Journal of Guidance,Control,and Dynamics,2004,27(5):829-838 |
| Click to display the text | |
| [4] | Hu X X,Wu L G,Hu C H,et al.Adaptive sliding mode tracking control for a flexible air-breathing hypersonic vehicle[J].Journal of the Franklin Institute,2012,349(2):559-577 |
| Click to display the text | |
| [5] | 曾宪法,王小虎,张晶,等.高超声速飞行器的干扰补偿Terminal滑模控制[J].北京航空航天大学学报,2012,38(11):1454-1458 Zeng Xianfa,Wang Xiaohu,Zhang Jing,et al.Disturbance compensated terminal sliding mode control for hypersonic vehicles[J].Journal of Beijing University of Aeronautics and Astronautics,2012,38(11):1454-1458(in Chinese) |
| Cited By in Cnki (5) | |
| [6] | 李静,左斌,段洣毅,等.输入受限的高超声速飞行器自适应Terminal滑模控制[J].航空学报,2012,33(2):220-233 Li Jing,Zuo Bin,Duan Miyi,et al.Adaptive terminal sliding mode control for air-breathing hypersonic vehicles under control input constraints[J].Acta Aeronautica et Astronautica Sinica,2012,33(2):220-233(in Chinese) |
| Cited By in Cnki (8) | |
| [7] | 黄喜元,王青,董朝阳.基于Backstepping的高超声速飞行器鲁棒自适应控制[J].系统工程与电子技术,2011,33(6):1321-1326 Huang Xiyuan,Wang Qing,Dong Chaoyang.Robust adaptive control of hypersonic vehicles via backstepping method[J].Systems Engineering and Electronics,2011,33(6):1321-1326(in Chinese) |
| Cited By in Cnki (9) | Click to display the text | |
| [8] | 后德龙,王青,王通,等.高超声速飞行器抗干扰反步滑模控制[J].北京航空航天大学学报,2014,40(1):80-85 Hou Delong,Wang Qing,Wang Tong,et al.Disturbance rejection sliding mode control of hypersonic vehicle based on backstepping method [J].Journal of Beijing University of Aeronautics and Astronautics,2014,40(1):80-85(in Chinese) |
| Cited By in Cnki | |
| [9] | 刘燕斌,陆宇平.基于反步法的高超音速飞机纵向逆飞行控制[J].控制与决策,2007,22(3):313-317 Liu Yanbin,Lu Yuping.Longitudinal inversion flight control based on backstepping for hypersonic vehicle[J].Control and Decision,2007,22(3):313-317 |
| Cited By in Cnki (46) | Click to display the text | |
| [10] | Fiorentini L,Serrani A,Bolender M A,et al.Nonlinear robust adaptive control of flexible air-breathing hypersonic vehicles[J].Journal of Guidance,Control,and Dynamics,2009,32(2):401-416 |
| Click to display the text | |
| [11] | Karagiannis D,Astolfi A.Nonlinear adaptive control of systems in feedback form:an alternative to adaptive backstepping[J].System & Control Letters,2008,57(9):733-739 |
| Click to display the text | |
| [12] | Fu J.Extended backstepping approach for a class of non-linear systems in generalised output feedback canonical form[J].IET Control Theory and Applications,2009,3(8):1023-1032 |
| Click to display the text | |
| [13] | Lee K W,Singh S N.Noncertainty-equivalent adaptive missile control via immersion and invariance[J].Journal of Guidance,Control,and Dynamics,2010,33(3):655-665 |
| Click to display the text | |
| [14] | Zhang J M,Li Q,Cheng N,et al.Adaptive dynamic surface control for unmanned aerial vehicles based on attractive manifolds[J].Journal of Guidance,Control,and Dynamics,2013,36(6):1776-1782 |
| Click to display the text | |
| [15] | Lu K F,Xia Y Q,Fu M Y.Controller design for rigid spacecraft attitude tracking with actuator saturation[J].Information Sciences,2013,220(20):343-366 |
