2. 中国航天空气动力技术研究院, 北京 100074;
3. 北京航空航天大学 航空科学与工程学院, 北京 100191
2. China Academy of Aerospace Aerodynamics, Beijing 100074, China;
3. School of Aeronautic Science and Engineering, Beijing University of Aeronautics and Astronautics, Beijing 100191, China
动力翼伞飞行器通常采用动力操纵来控制飞行器的航迹倾角.在伞体后缘不动的情况下,每一个推力值都对应一种定直飞行状态,且推力值越大,航迹倾角和迎角也越大.因此在有限的迎角范围内,必然存在推力值的上限,过大的推力会导致伞体达到失速迎角而发生倾覆[1]. 然而在一款小型动力翼伞飞行器的试飞过程中,尽管推力已经限制在按照上述方法要求的上限以内,但由于动力增加速度过快,初期还是很容易出现伞体倾覆的现象.因此非常有必要建立纵向动力学模型,研究翼伞动态操纵初期翼伞参数的变化过程.研究翼伞纵向平面的运动可以采用三自由度模型,即将整个翼伞系统视作一个刚体,在纵向平面内有两个平动和一个转动自由度[2,3,4].但是此类模型忽略了伞体和载荷物之间的相对运动,当载荷物在运动过程中和伞体发生剧烈的相对俯仰时,三自由度模型就无法精确模拟翼伞的动力学响应.因此多数翼伞的动力学仿真均考虑了伞体相对于载荷物的纵向俯仰自由度[5,6,7,8].当只研究翼伞的推力响应时,可以假设所有的运动都在纵向平面内.
本文首先建立动力翼伞纵向四自由度模型.该模型将伞体和伞绳作为一个整体,在纵向具备3个自由度,载荷物具有绕系挂点的一个摆动自由度.用所建立的动力学模型,分析翼伞在快速大动力操纵下所带来的迎角剧增的问题,提出较为合适的动力操纵速率.同时通过仿真计算,证明利用这种快速动力操纵在着陆时实现雀降减速的可行性. 1 纵向动力学建模 1.1 模型描述
某带动力的七气室翼伞(图 1),平面形状为矩形,采用相对厚度为12%的Clark-Y翼型,展长lw=1.68 m,弦长c=0.7 m,前缘切口长h=0.07 m,下反角β=32.5°,伞体质量m1=0.25 kg.载荷物为圆柱形,质量,载荷物前方带有一个电机直驱螺旋桨的推进系统,最大拉力为8 N.
 |
| 图 1 翼伞外形 Fig. 1 Shape of parafoil |
分析翼伞纵向运动,可以将其简化为图 2中模型进行分析.其中AB代表伞体,OA和OB代表伞绳边界,其他伞绳均在其中,坐标原点O为伞绳与载荷物的系点,O1为伞体的重心,O2为载荷物的重心,F为伞体的焦点,C为线段OO1的中点.图 2中其余小写字母均表示所指的长度或角度.伞体受到的气动力和力矩的作用点选为F;伞绳的阻力则近似假设作用在C点.
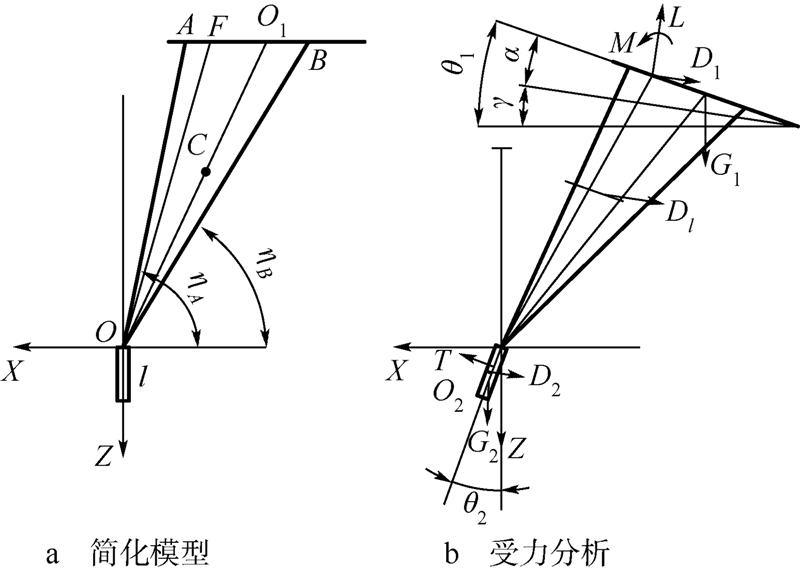 |
| 图 2 翼伞的参数定义 Fig. 2 Definition of parafoil parameters |
翼伞在纵向的运动中,伞绳始终处于绷紧状态,因此可以将“伞-伞绳”系统看作一个整体,且由于伞绳较轻,故忽略其质量,仅考虑其阻力. 1.2 动力学方程推导
在平面大地的假设下,忽略所有转动部件,伞体伞绳和载荷物分别可以视为两个六自由度刚体.建立两个刚体的体轴系,原点均为各自质心.其中伞体伞绳体轴系的X1轴和AB平行,方向向前;Z1轴在对称面内垂直X1轴向下;Y1轴垂直对称面向右.载荷物体轴系的X2轴垂直于载荷物长度方向,向前为正;Z2轴在对称面内垂直X2轴向下;Y2轴垂直对称面向右.
除两个体轴系外还需要建立一个绝对轴系,原点、X轴和Z轴如图 2所示,Y轴垂直对称面向右.
在上述坐标系下,列写两个刚体通用的动力学方程:
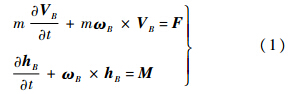
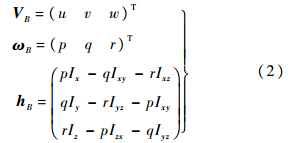
式(2)中和I有关的均为物体的惯量和惯性积.将(2)式代入式(1),只考虑纵向平面的运动,化简得
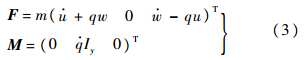
根据式(3)可以分别写出两个刚体的纵向动力学方程:
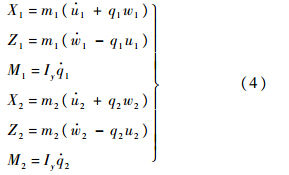
根据几何关系,可以获得两个刚体之间的牵连方程:
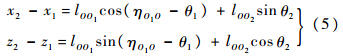
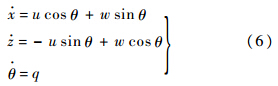
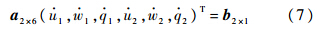
式(4)中等号左边代表合外力和合外力矩,均由相应物体状态参数决定,故结合式(4)、式(6)的第3式、式(7),通过化简,可以得到以下形式的表达式:
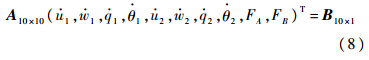
本文中的升力系数和诱导阻力系数采用自编涡格法程序进行求解.与工程估算公式相比,涡格法可以充分反映翼伞的小展弦比、大下反角的特点对气动性能的影响.由于涡格法基于流体定常、无黏、无旋、不可压的假设,因此只能对升力和诱导阻力做出估算.但是该方法仍具有计算快捷、在小迎角下精度较高的特点.因此替代工程估算公式来对翼伞的升力特性做出快速估算,并具有很好的效果[9,10].
本翼伞采用自编涡格法程序计算的气动力包括升力、诱导阻力、俯仰力矩.其他成分的阻力采用Lingard的工程估算方法进行计算[11],包括伞体零升阻力CD0、伞绳阻力CDl和载荷物阻力CDS.
伞体零升阻力CD0=0.07.其作用点近似认为是伞体的焦点,其组成如表 1所示.
| 阻力类型 | 阻力系数 |
| 基本翼型的阻力 | 0.015 |
| 表面粗糙造成的阻力 | 0.004 |
| 前缘切口阻力 | 0.5 h/c |
| 伞绳与翼面固定端、翼稍稳定幅的阻力 | 0.001 |
伞绳阻力CDl=nRdlcos3αl/S.其中n为伞绳数目,R为伞绳的平均长度,dl为伞绳直径,S为翼伞的面积,αl为伞绳的法面与来流的夹角.在本文的计算中近似将所有伞绳的空气阻力视为相等,且αl=α+(π+θ1+θ2)/2.同时将其合力作用点近似认为是△ABO中位线的中点.
载荷物阻力CDS=ld/S.其中l为载荷物的长度,d为载荷物的直径.由于载荷物形状为简单圆柱体,其作用点近似认为在圆柱的中心. 1.5 附加质量求解
翼伞在空气中做变速运动时,周围流体的动量和动量矩也在发生改变,因此作用于翼伞上的除了通常考虑的定常气动力以外,还有非定常气动力部分.非定常气动力在位势流理论中可以处理为附加质量考虑,即在合外力中增加由于附加质量引起的力[12,13,14].
翼载荷较小的飞行器,其附加质量不能忽略.而若物体的外形为伞状,其附加质量往往会数倍于其实际质量.故在研究翼伞动力学特性时伞体的附加质量力不能忽略.
本文的附加质量求解采用Lissaman的估算方法[15]:
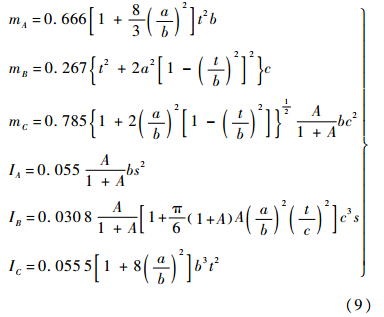
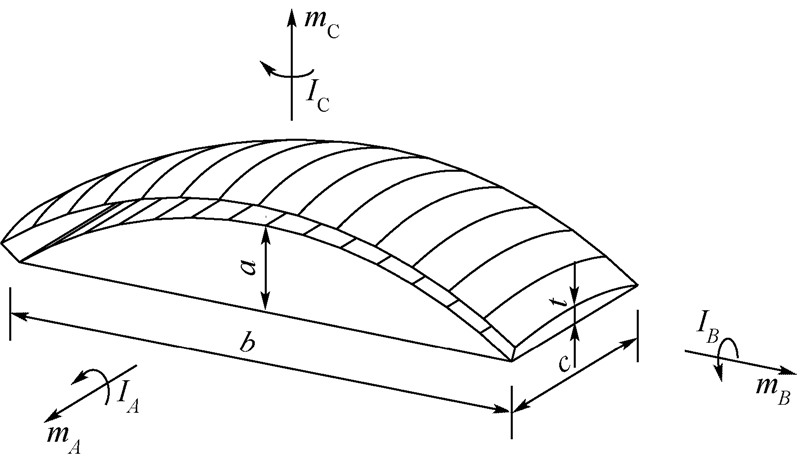 |
| 图 3 伞体尺寸 Fig. 3 Size of canopy |
在文中的纵向动力学模型中只需用到其中的3个值:mA,mC,IB.
根据Lissaman的推导,由于物体变速运动而使周围流体发生动能的变化,在本文的纵向运动中其大小为[15]
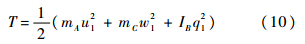
物体对流体的冲量和冲量矩为[15]
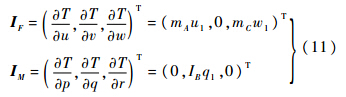
流体对物体的附加质量力和力矩为[15]
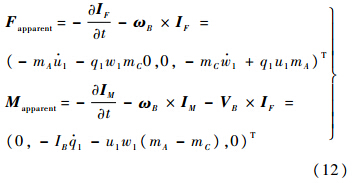
2 推力操纵响应 2.1 推力操纵初期的翼伞失速问题
在翼伞的飞行过程中,如果缓慢增加推力,翼伞各项参数变化缓慢,整个过程可以引入准静态假设,采用静力学分析方法可以简化问题并获得较好的结果.此方法往往被用来分析飞行器的静操纵性.采用上述方法可以得到翼伞飞行的迎角随推力增大而增大的结论,翼伞的失速迎角则导致推力上限的存在.而在实际操纵过程中,动力增加往往不符合准静态假设,过快的操纵推力会导致各个状态参数剧烈变化,并且出现大于最终稳态值的超调量.迎角作为翼伞的一个状态参数,不可避免地也会出现超调,如果迎角变化的峰值超过了其失速迎角,则伞体将发生失速倾覆.
对于飞行状态较为简单的动力翼伞飞行器,需要增加动力的情况往往集中于翼伞起飞爬升阶段或在空中的爬升阶段,因此研究定直平飞状态下的动力输入响应.对于推力输入增量,其参数变化情况如图 4~图 8所示.翼伞的动力输入采用线性增加模型:
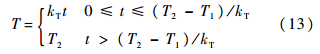
利用上述模型解出本文中翼伞飞行器的定直平飞状态为α=6.99°,θ2=6.81°,v=6.3 m/s,T=4.15 N.在上述平飞状态的基础上进行动力操纵,推力终值T2=6 N,增加速率kT=3.7 N/s,伞体的迎角、爬升角、伞体和载荷物的速度和俯仰角、物-伞的相对转角随时间的变化情况如图 4~图 8所示. 可以从图中看出动力输入初期伞体各个状态量迅速变化,并在此后的震荡中逐渐收敛至稳态值.翼伞从平飞状态转为定直爬升状态.在动力输入初期伞体和载荷物会出现较大的相对摆动,并逐渐衰减.计算结果反应出了物伞相对运动过程.
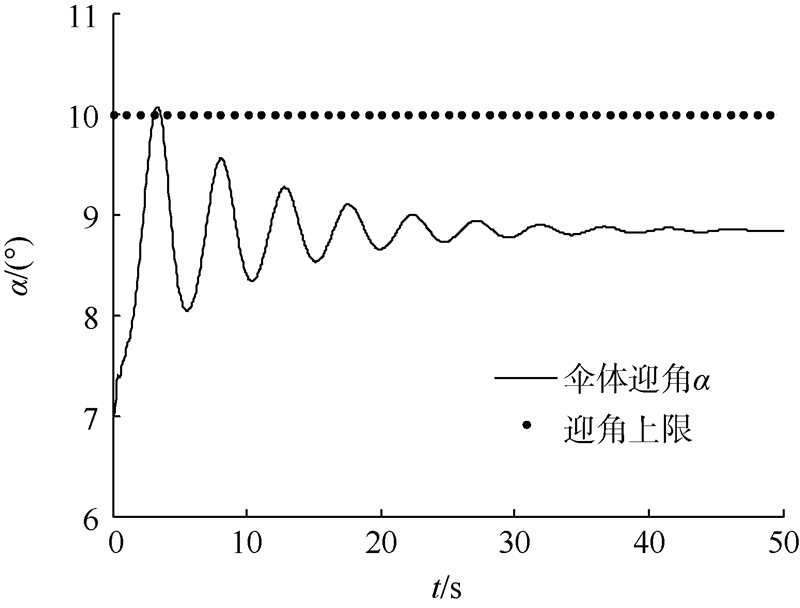 |
| 图 4 伞体的迎角随时间的变化 Fig. 4 Angle of attack of canopy vs time |
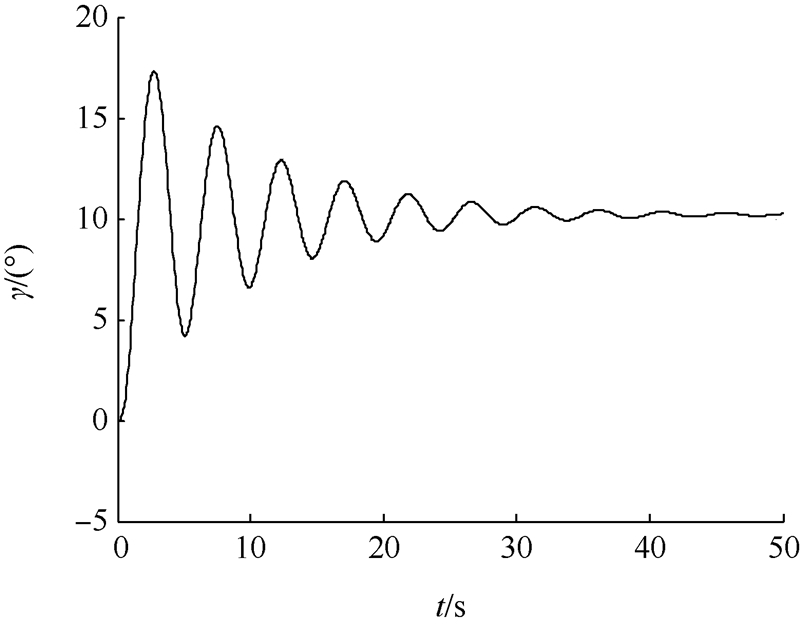 |
| 图 5 伞体的爬升角随时间的变化 Fig. 5 Climbing angle of canopy vs time |
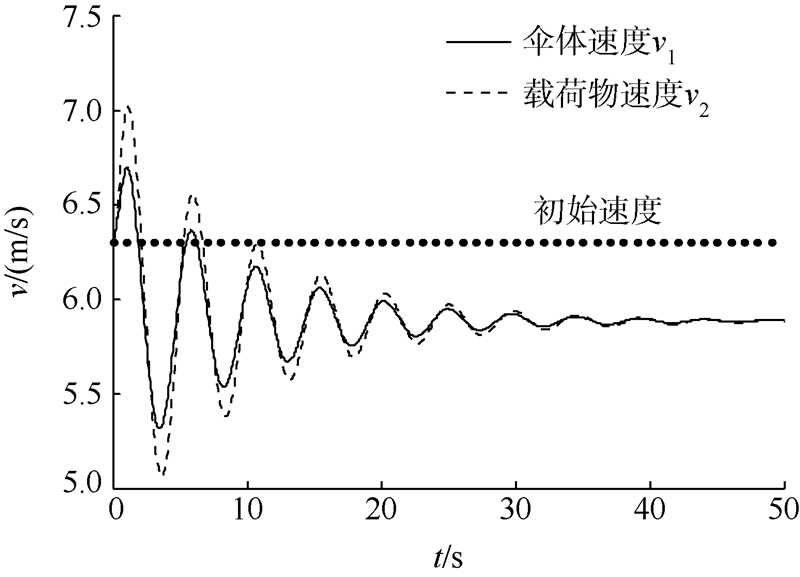 |
| 图 6 伞体和载荷物的速度随时间的变化化 Fig. 6 Velocity of canopy and payload vs time |
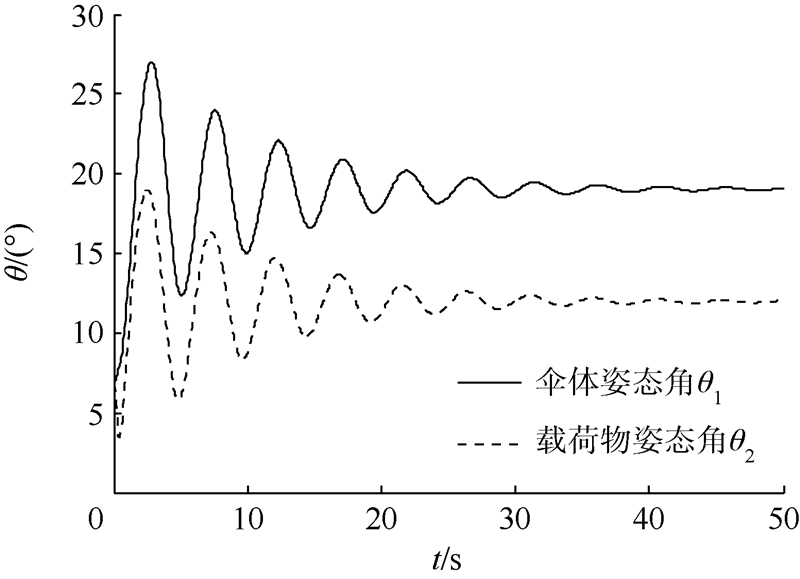 |
| 图 7 伞体和载荷物的姿态角随时间的变化 Fig. 7 Attitude angle of canopy and payload vs time |
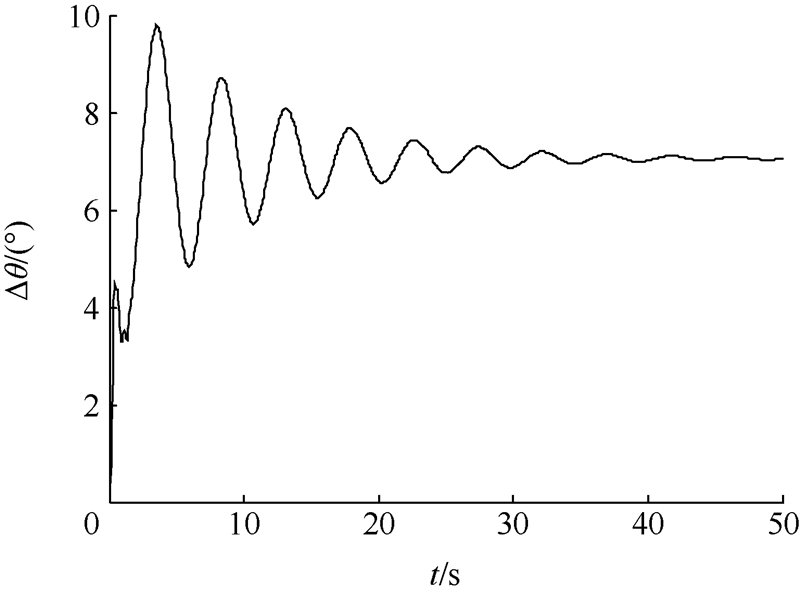 |
| 图 8 物-伞的相对转角随时间的变化 Fig. 8 Relative attitude angle between canopy and payload vs time |
本文中的翼伞失速迎角约为10°[16].在迎角的变化过程中,尽管最后的稳态值低于上限,但是初期的快速增长很可能使峰值超出上限而失速.因此在进行动力操作时,应对典型动态过程深入研究以避免操纵过程中发生的伞体失速倾覆现象. 2.2 推力操纵包线
在上述算例中当操纵速率逐渐减慢,各个状态量的峰值也随之下降,图 9为相同推力终值T2=6 N,不同操纵速率下迎角的变化情况.kT分别取值为3.7,0.8,0.5 N/s.
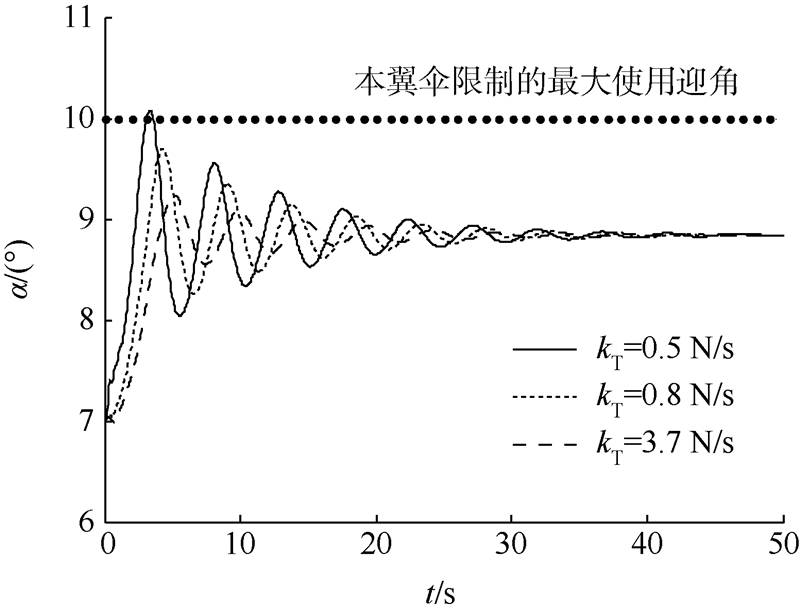 |
| 图 9 不同推力操纵速率情况下的迎角响应 Fig. 9 Angle of attack response after different throttle control rates |
由图 9可知,随着推力增速的减小迎角的最大峰值也逐渐减小.对于构型确定的翼伞飞行器,若想从平飞状态转为一定爬升角飞行状态,并且此过程中保持迎角始终不超过上限值,则动力输入的速率必须满足一定条件.即在确定的最终推力值下推力增长速率有上限.图 10为计算获得的本翼伞飞行器由平飞转爬升的推力操纵包线.图中的推力操纵边界左侧和平飞需用推力线右侧所包含的区域为操纵可行域.
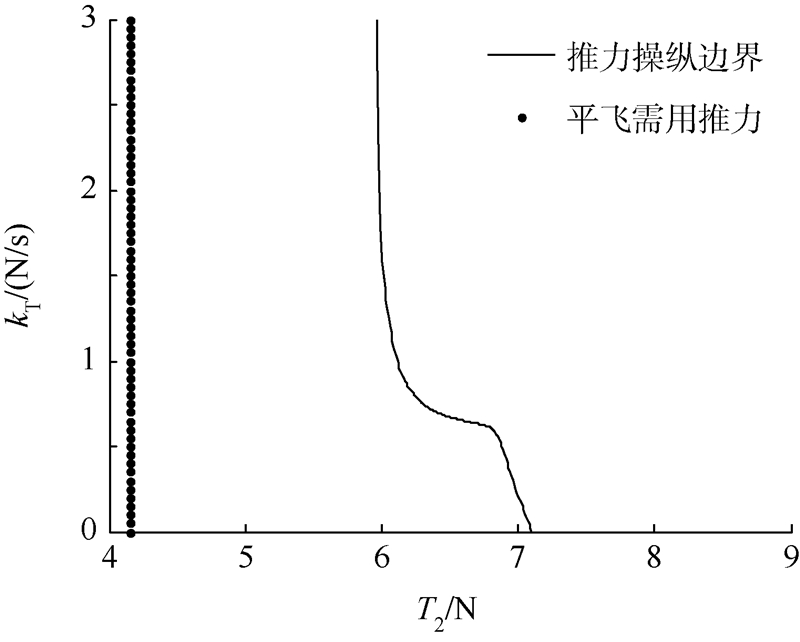 |
| 图 10 平飞状态下推力操纵包线 Fig. 10 Throttle control envelope of level flight |
由图 10可知,在平飞状态下,当推力终值小于5.9 N时,可以以任意速率增加推力;推力终值不应超过7.1 N,否则迎角的稳态值超过翼伞的迎角上限. 3 推力操纵下的雀降着陆 3.1 着陆接地分析
由于本翼伞飞行器的载荷物长细比较大,接地碰撞后会产生额外的运动向前倾倒.而动力系统位于载荷物的前端,因此有必要对接地后的运动进行分析,研究载荷物接地前后的能量变化情况,以选择合适的方法减缓对载荷物前端的冲击.在本翼伞试飞过程中载荷物下端包裹着较软的泡沫获得缓冲.因此本文中假设载荷物在接地碰撞后不再上跳,只是绕底端旋转,同时伞绳立刻处于松弛状态而忽略其对载荷物的拉力.
图 11为接地前的示意图.其中P点为接地点;v的第1位下标为2代表是载荷物的状态,第2位下标为x和z分别代表水平和竖直方向,第3位下标为1和2分别代表接地碰撞前和碰撞后;IPx和IPz表示接地时地面对载荷物的冲量;ω21表示载荷物接地前后的角速度;θ21表示载荷物接地时的俯仰姿态角.对载荷物运用冲量定理和冲量矩定理:
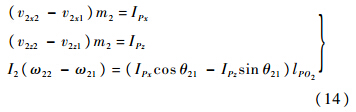
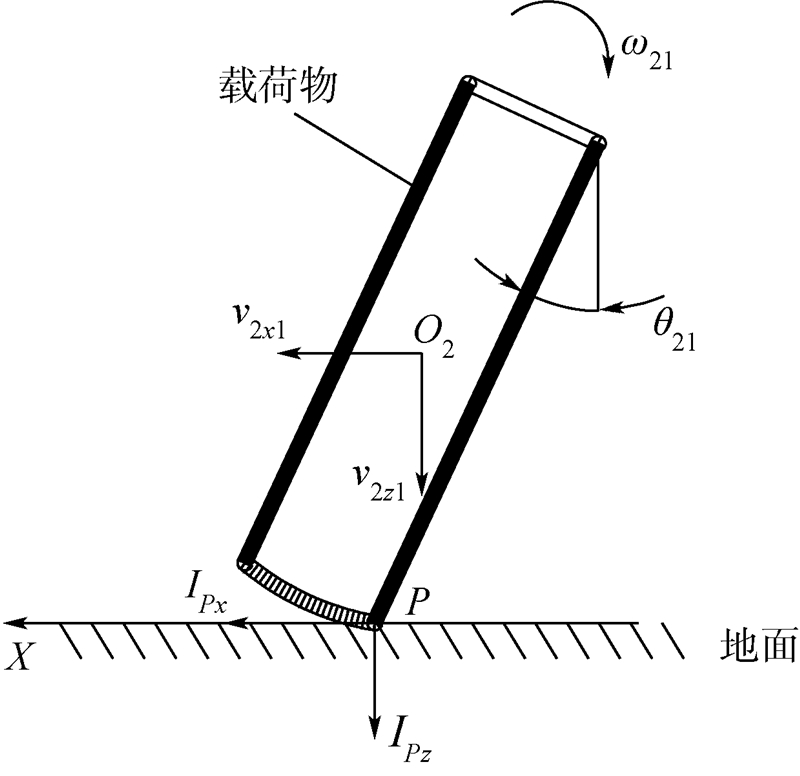 |
| 图 11 载荷物着陆分析 Fig. 11 Landing analysis of payload |
由于载荷物底部包裹软质泡沫材料,碰撞后瞬间的运动方式为绕接地点旋转,因此质心速度和角速度具有如下关系:
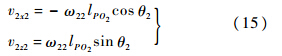
接地碰撞后载荷物旋转角速度为
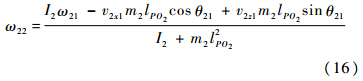
以地面为重力势能参考面,接地碰撞后载荷物的机械能为
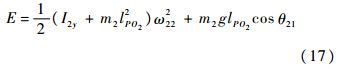
由于动力翼伞主要设计要求为获得最长的续航时间,即平飞时伞体处于升阻比最高的迎角状态.伞体和载荷物之间的相对几何位置就依据此条件设计.但这将导致翼伞在无动力滑翔状态时,始终处于不合适的迎角.若采用传统后缘下拉方式实现雀降[3,17],将导致前伞绳松弛而使伞体倾覆.
以本翼伞为例,无动力状态的稳定飞行迎角约为3°.在此状态下以120 (°)/s的速度输入10°幅值的后缘操纵量,并以此速度恢复后缘的偏转量.图 12、图 13为操纵后伞体迎角和伞绳拉力的变化情况.可以看出在大约0.15 s后前伞绳拉力为负,故此后伞体塌陷,仿真结果无意义.造成这种情况的原因主要是初始滑翔状态迎角过小,后缘操纵后伞体在低头力矩的作用下先开始转动,伞体迎角减小.在翼伞整体获得减速前,前伞绳已经到达松弛状态,故后缘操纵方式较难实现动力翼伞的雀降.
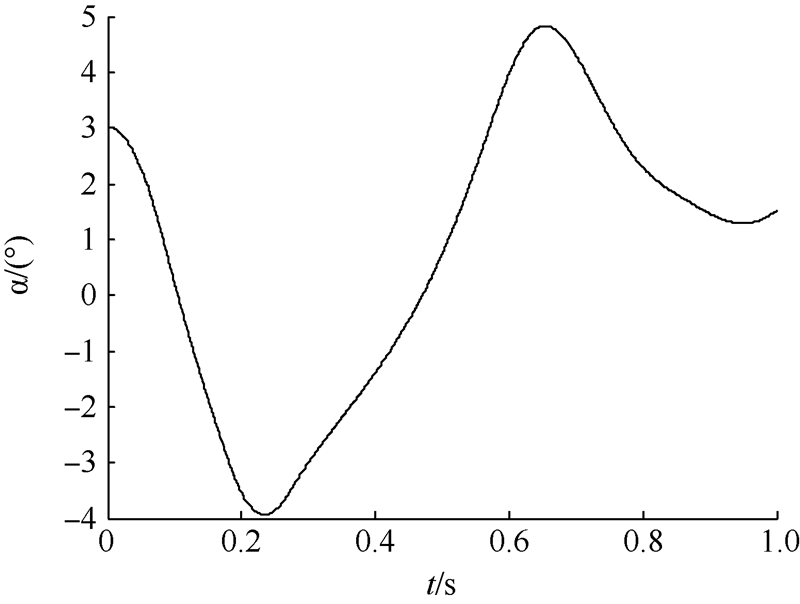 |
| 图 12 后缘下偏雀降方式中伞体迎角响应曲线 Fig. 12 Angle of attack response of flap down flare |
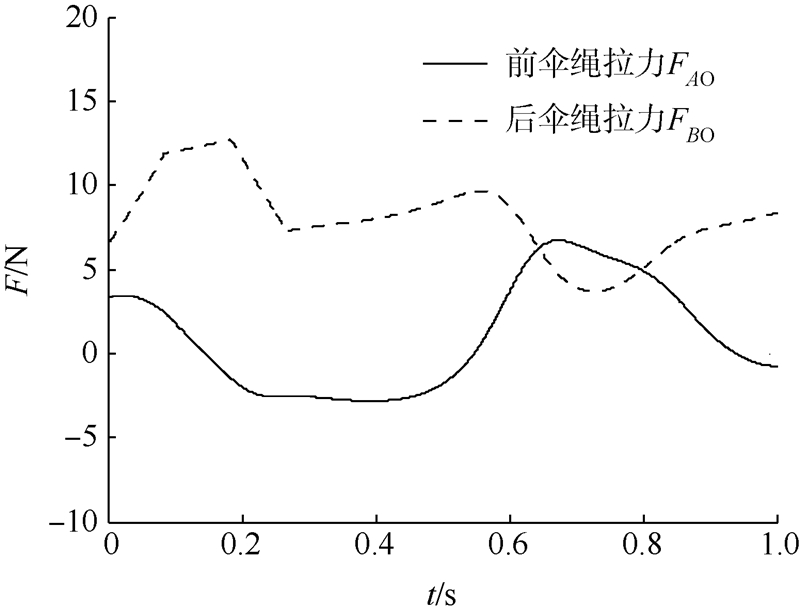 |
| 图 13 后缘下偏雀降方式中伞绳拉力响应曲线 Fig. 13 Suspension line tension response of flap down flare |
因此对于动力翼伞需要采取一种更为安全的雀降方式.本文研究一种短时间增加动力以改变翼伞状态参数的操纵,即接近地面时迅速增大动力,并将此作为另一种雀降方法.本文采用梯形波输入操纵,动力线性增加和减少速率相等,并在峰值保持一段时间,具体表达式为
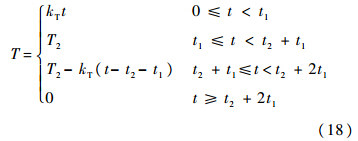
本文算例中取峰值推力T2=7 N,推力增长率kT=20 N/s,推力增长时间t1=T2/kT,推力峰值保持时间t2=0.5 s,见图 14.无动力滑翔阶段的状态参数为α=3.01°,θ2=-5.02°,γ=-25.55°,v=7.74 m/s.
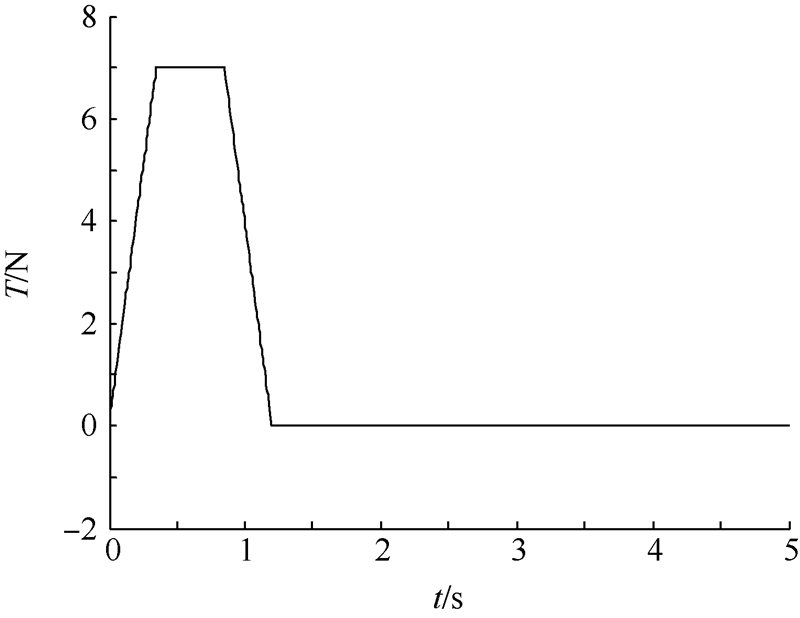 |
| 图 14 推力操纵曲线 Fig. 14 Throttle control curve |
对于上述操纵输入,求得载荷物最低点的高度和接地前后的机械能变化情况如图 15~图 17所示.
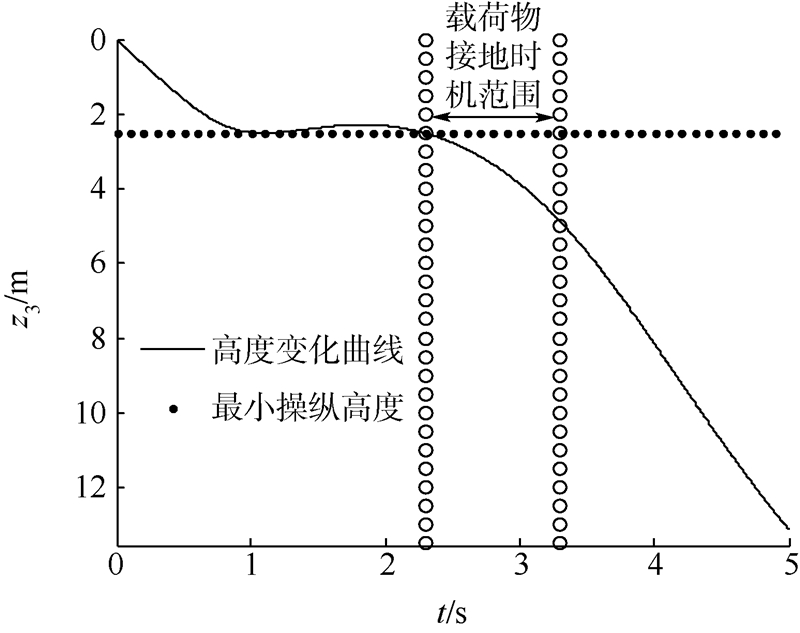 |
| 图 15 载荷物最低点高度随时间的变化 Fig. 15 Position of the lowest point of payload vs time |
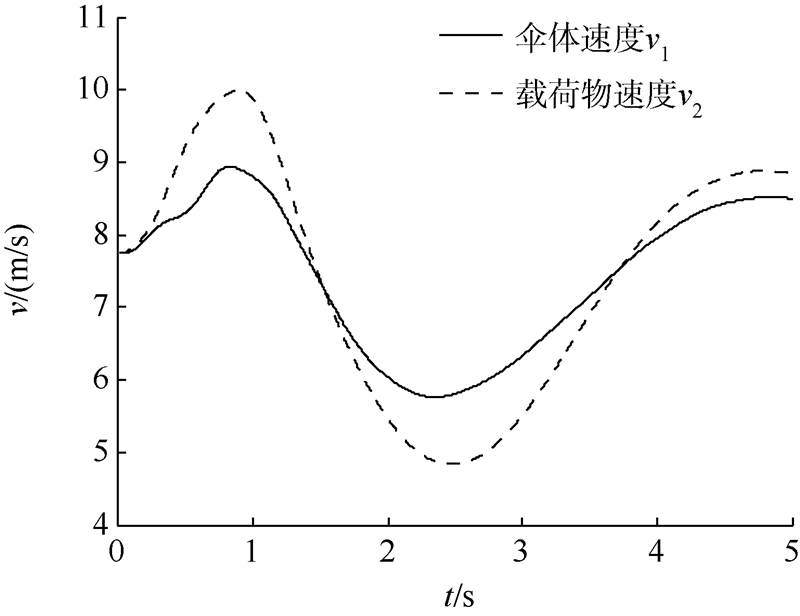 |
| 图 16 雀降操纵后物伞速度随时间的变化 Fig. 16 Velocity of canopy and payload vs time after flare control |
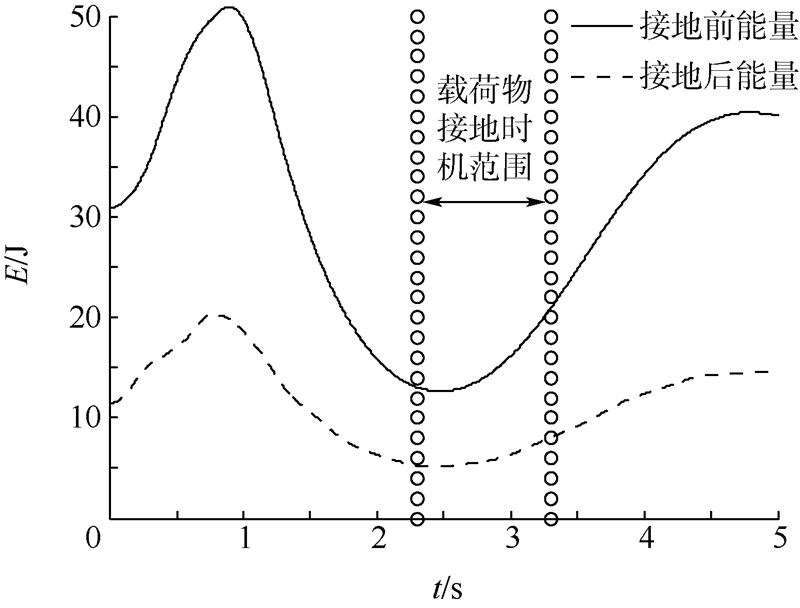 |
| 图 17 载荷物机械能随时间的变化 Fig. 17 Mechanical energy of payload vs time |
由图 17可知,载荷物在接地前后的能量随时间的变化趋势基本一致,因此当接地前能量较小时,接地后载荷物的能量也很小,对载荷物正面的动力系统的冲击也较弱.
从上述轨迹线和能量变化曲线图中选择接地时机,需要满足以下条件:
1) 高度应低于之前所有轨迹点的高度,保证此前不碰到地面;
2) 能量值应尽可能低,减少冲击载荷;
3) 该点前后能量值增长不是很剧烈,以便有足够长的窗口时间来操控;
4) 该点应该在动力关闭之后,以防接地冲击时损坏螺旋桨和电机.
图 15和图 17中两条带圈线的区间为可以作为接地时机,按照图 14的动力操纵方式,本翼伞最佳接地时间大概在动力操纵后的2.3~3.3 s,即在距地面2.6~4.8 m的高度输入图 14中的动力操纵.计算结果证明采用推力操纵的方法可以实现动力翼伞的雀降,能达到较好的减速效果,同时具有较宽的窗口时间. 4 结 论
本文用所建立的纵向四自由度模型,计算求解了平飞状态下动力阶跃输入后翼伞状态参数的动力学响应.各参数出现波动并最终稳定于新的爬升状态下的参数.在波动过程中伞体的迎角较容易超过失速迎角,这就解释了翼伞飞行器大动力操纵初期翼伞倾覆的现象.
通过对多种推力增量下的翼伞动力学响应计算,得到平飞状态的推力操纵包线.当推力增幅较小时,操纵时推力增加速率并无限制;当推力增幅较大时,增加速率必须小于限制值才能使翼伞从水平状态安全过渡至爬升状态,并且这个限制值随着推力增幅变大而减小;当推力增幅最大时,翼伞稳定飞行的迎角恰好为失速迎角.
由于动力翼伞和普通翼伞设计状态的不同,动力翼伞在采用普通雀降方式(后缘下偏)时,较易进入前伞绳松弛的状态,影响飞行安全.因此提出短暂的动力操纵实现雀降的方法.计算表明,在降落阶段短时间的推力操纵可以大幅度地改变翼伞的状态参数.通过载荷物接地前后机械能变化情况以及最低点的轨迹求解,可以获得一个较宽的雀降窗口时间,在该阶段内载荷物的机械能处于较低水平,可以有效减少对载荷物尤其是前部动力系统的冲击.因此利用短时间动力操纵实现动力翼伞的雀降着陆是可行的.
| [1] | Yang H,Song L,Liu C,et al.Study on powered-parafoil longitudinal flight performance with a fast estimation model[J].Journal of Aircraft,2013,50(5):1660-1668 |
| Click to display the text | |
| [2] | 张俊韬,侯中喜.动力翼伞系统纵向动力学建模研究[J].系统仿真学报,2010,22(11):2541-2544 Zhang Juntao,Hou Zhongxi.Research on longitudinal dynamic modeling of powered parafoilsystem[J].Journal of System Simulation,2010,22(11):2541-2544(in Chinese) |
| Cited By in Cnki (1) | |
| [3] | 张兴会,朱二琳.翼伞系统雀降性能及控制研究[J].航天控制,2012,30(1):29-32 Zhang Xinghui,Zhu Erlin.Thestudy of the flare-landing performance and control of parafoilsystem[J].Aerospace Control,2012,30(1):29-32(in Chinese) |
| Cited By in Cnki | |
| [4] | Goodrick T F.Simulationstudies of the flight dynamics of gliding parachute systems[R].AIAA-79-0417,1979 |
| [5] | 熊菁.翼伞系统动力学与归航方案研究[D].长沙:国防科学技术大学,2005 Xiong Jing.Research on the dynamics and homing project of parafoilsystem[D].Changsha:National University of Defense Technology,2005(in Chinese) |
| Cited By in Cnki (29) | |
| [6] | Strickert G,Witte L.Analysis of the relative motion in a parafoil-load-system[R].AIAA-2001-2013,2001 |
| Click to display the text | |
| [7] | Yakimenko O A.On the development of a scalable 8-DOF model for a generic parafoil-payload delivery system[R].AIAA-2005-1665,2005 |
| Click to display the text | |
| [8] | Prakash O,Ananthkrishnan N.Modeling and simulation of 9-DOF parafoil-payload system flight dynamics[R].AIAA-2006-6130,2006 |
| Click to display the text | |
| [9] | 熊菁,秦子增.涡格法计算全展开翼伞的气动力[J].湖北航天科技,2005(5):5-11 Xiong Jing,Qin Zizeng.Calculation of full-span parafoil with vortex lattice method[J].Aerospace Science and Technology of Hubei Province,2005(5):5-11(in Chinese) |
| [10] | 钱翼稷.空气动力学[M].北京:北京航空航天大学出版社,2009:150-169 Qian Yiji.Aerodynamics[M].Beijing:Beijing University of Aeronautics and Astronautics Press,2009:150-169(in Chinese) |
| [11] | Lingard J S.Ram-air parachute design[C]//Precision Aerial Delivery Seminar,13th AIAA Aerodynamic Decelerator Systems Technology Conference.Clearwater Beach:ADS Technical Committee,1995 |
| [12] | Barrows T M.Apparentmass of parafoils with spanwisecamber[J].Journal of Aircraft,2002,39(3):445-451 |
| Click to display the text | |
| [13] | Cockrell D J.Apparentmass:its history and its engineering legacy for parachute aerodynamics[R].AIAA-91-0827,1991 |
| Click to display the text | |
| [14] | 熊菁,秦小波,程文科.降落伞系统附加质量的研究[J].中国空间科学技术,2002(4):34-40 Xiong Jing,Qin Xiaobo,Cheng Wenke.The added mass research in parachute system[J].Chinese Space Science and Technology,2002(4):34-40(in Chinese) |
| Cited By in Cnki (17) | |
| [15] | Lissaman P B S,Brown G J.Apparentmass effects on parafoildynamics[R].AIAA-93-1236,1993 |
| Click to display the text | |
| [16] | Nicolaides J D.Parafoilwind tunnel tests[R].AD731564,1971 |
| Click to display the text | |
| [17] | 赵秋艳.翼伞雀降技术[J].航天返回与遥感,1999(2):5-9 Zhao Qiuyan.Flaremaneuver of ram-air parafoil[J].Spacecraft Recovery & Remote Sensing,1999(2):5-9(in Chinese) |
| Cited By in Cnki (9) |




