随着遥感探测技术和制导技术的飞速发展,导弹的突防受到了越来越严重的威胁.为了有效地提高导弹的生存能力和突防能力,以美国为首的各军事强国都在积极研究隐身技术[1].由于隐身性能与飞行器外形密切相关[2],因此飞行器外形设计不仅要考虑气动特性,同时也要考虑隐身特性,飞行器气动隐身一体化设计成了一个重要的研究问题[3]. 廖炎平等提出基于多属性决策的多目标优化方法对跨声速前掠翼的气动隐身特性进行了细致研究[4];张昆等分析了导弹截面形状对导弹隐身特性的影响[5];楚亮等实现了基于Pareto遗传算法的非圆截面弹体气动隐身多目标优化[6].
战术导弹的气动隐身性能属于多目标优化问题,常用的多目标优化算法有加权系数法、Pareto多目标遗传算法和物理规划法等.加权系数法在求解多目标问题时需要反复调节权重,计算耗时.Pareto多目标遗传算法能准确地求出多目标问题的非劣解集,但如果约束条件不够准确,计算量偏大.而物理规划,能与任何优化算法结合,灵活性高,并且不需要设置权值,只要给定偏好就可以获得满足偏好的结果[7]. 将物理规划与遗传算法相结合,在求解战术导弹气动隐身多目标优化问题时,设计者无需对气动隐身性能进行折衷,只要根据工程需求给定偏好,就能得到满足工程需求的非劣解.通过变量筛选,将战术导弹外形尺寸对气动隐身综合特性的影响度进行排序,不仅降低了设计变量维度,减少了计算成本;而且忽略了不重要的尺寸因素,降低了战术导弹优化复杂程度.最后,采用径向基函数(RBF,Radial Basis Function)代理模型[8, 9]代替耗时的高精度仿真模型,进一步减少了计算成本,提高了计算效率.
1 战术导弹气动隐身性能分析方法 1.1 气动分析模型
常用的战术导弹气动分析方法有工程估算法与计算流体力学方法.本文采用基于DATCOM[10]气动估算软件解算导弹的气动参数.DATCOM的计算速度快,在满足精度要求的前提下,用来代替漫长的CFD计算,能有效减少计算成本.
以文献[11]中的导弹模型为例,计算其在马赫数为1.75,雷诺数为2.00×106的工况下,不同攻角下导弹的法向力系数.如图 1所示,在战术导弹的方案设计阶段,DATCOM计算所得的气动参数值能满足设计精度要求.
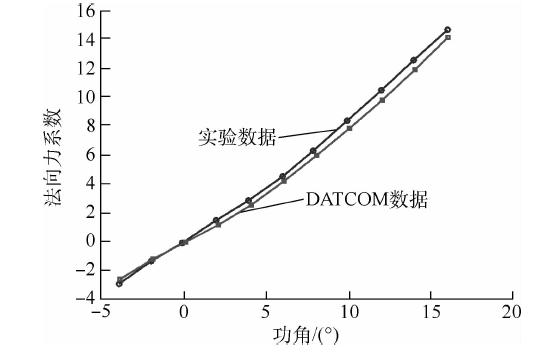 |
| 图 1 法向力系数的DATCOM计算数据与实验数据对比Fig. 1 Comparison of normal force coefficient from DATCOM and experiment |
常用的雷达散射截面积(RCS,Radar Cross Section)解算方法有绕射法、光学法、追踪法和矩量法等.本文采用基于矩量法的FEKO电磁计算软件解算战术导弹的隐身性能.为保证与气动分析模型的一致性,本文利用DATCOM对导弹几何参数的命名标准,通过UG二次开发创建了战术导弹的三维隐身分析几何模型.
为验证FEKO解算RCS的精度.利用NASA金属杏仁体[12]在入射波频率为7 GHz,采用水平极化和垂直极化两种扫描方式下求解的RCS值与实验数据对比如图 2所示.FEKO计算所得的RCS能满足设计精度要求.
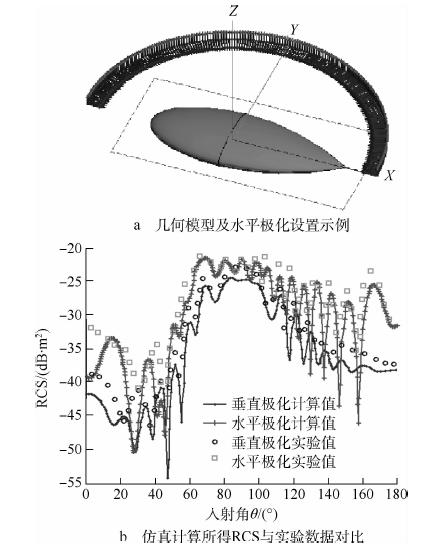 |
| 图 2 NASA杏仁体RCS的FEKO计算结果与实验数据对比Fig. 2 Comparison of RCS between NASA almond’s results from FEKO and experiment |
战术导弹气动隐身多目标优化问题可以用如下数学形式描述:
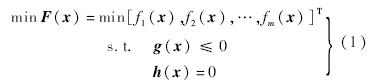
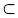 Rm是m维目标函数矢量,x=[x1,x2,…,xn]∈X
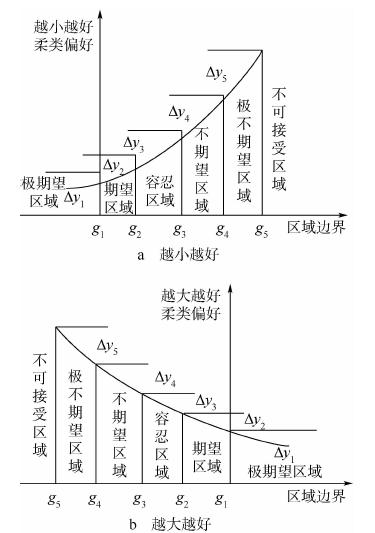
Rm是m维目标函数矢量,x=[x1,x2,…,xn]∈X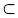 Rn是n维设计变量,针对气动隐身多目标优化问题,X即为战术导弹的几何外形参数;
h(x)=[h1(x),h2(x),…,hp(x)]定义了p个等式约束;g(x)=[g1(x),g2(x),…,gq(x)]定义了q个不等式约束.
Rn是n维设计变量,针对气动隐身多目标优化问题,X即为战术导弹的几何外形参数;
h(x)=[h1(x),h2(x),…,hp(x)]定义了p个等式约束;g(x)=[g1(x),g2(x),…,gq(x)]定义了q个不等式约束.2.2 物理规划方法
物理规划(physical programming)[13]是Messac于1996年提出的一种处理多目标优化设计问题的策略,基本思想是引入偏好函数,将不同的目标函数转化为同量级的“满意度”目标函数,即将多目标问题转化为单目标问题处理.
物理规划的核心思想是偏好函数,所谓偏好函数是指用户可自行根据设计优化思想决定目标函数取到何值时为好,取到何值时为不好,即规定了“好与坏”的界限.战术导弹气动隐身多目标优化的目标函数可归纳为:阻力系数最小,升阻比最大,RCS最小(前向、后向或全向)等.物理规划的偏好函数可分为3类:越小越好(SIB),越大越好(LIB),越趋于某值越好(CIB),针对战术导弹气动隐身多目标优化问题选取SIB和LIB作为主要叙述对象(如图 3所示).
 |
| Δy1~Δy5—穿越该区域时偏好函数的变化值.区域划分应遵循均分原则,即保证每个目标函数在穿越该区间内造成的偏好函数变化值相等.图 3 偏好函数区域划分图Fig. 3 Preference function regions for ith generic criterion |
SIB和LIB偏好函数方程的构造,需要给定5个边界值,利用边界值可以准确地描述各偏好函数,进而求解出多目标问题的总偏好,最后将总偏好代入优化函数中进行优化,得到相应的非劣解.物理规划优化方法的流程如图 4所示.
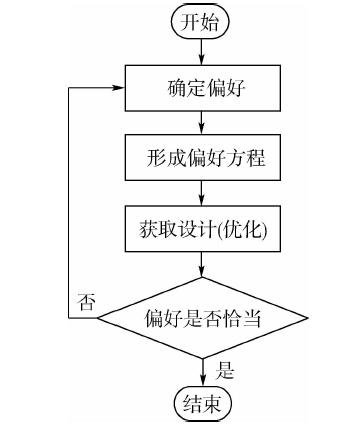 |
| 图 4 物理规划流程Fig. 4 Flowchart of physical programming |
与线性加权法相比,物理规划具有以下优势:①无需反复调节权重,减少了计算成本;②线性加权法无论如何调整权重都无法获得非凸Pareto非劣解,而物理规划通过偏好函数去逼近Pareto非劣解,能很好地获得非凸Pareto非劣解.
2.3 变量筛选
针对战术导弹气动隐身多目标优化,其设计变量维度常在几十到上百的数量级.优化问题的计算成本随设计变量维度的增加而呈几何级数增长,造成“维度灾难”.为了降低战术导弹气动隐身多目标优化问题的计算成本,有必要对设计变量进行筛选,去掉对优化目标影响小的设计变量,以降低优化问题的维数.
利用试验设计方法(DoE,Design of Experiment)对问题进行采样,结合方差分析(ANOVA,Analysis of Variance)可以很好地筛选出问题的关键因素.变量筛选的流程如图 5所示.
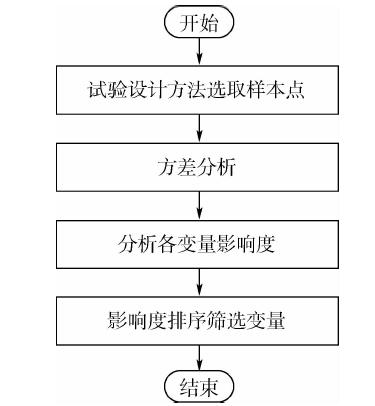 |
| 图 5 变量筛选流程Fig. 5 Flowchart of variable selection |
经分析发现,选取Box-Behnken为基于方差分析的变量筛选的DoE时,能达到样本规模小、结果精确度高的要求,而基于投影均布性的DoE不适用于基于方差分析的变量筛选.
2.4 代理模型
针对战术导弹气动隐身多目标优化高精度仿真模型计算成本高的问题,采用代理模型(surrogate model)来降低计算成本.代理模型,是指通过数学手段构造的计算量小、计算结果与数值分析或物理实验结果相近的近似数学模型,以代替原分析模型或物理实验用于优化设计[14].
径向函数是以未知点与数据点之间的欧式距离为自变量的一类函数.以径向函数为基函数,通过线性叠加构造出来的代理模型即为径向基函数代理模型.该方法通过径向函数将多维问题转化为一维问题,从而大大简化了建立模型的计算成本,并保证了较高的精度.
径向基函数的基本形式如下:
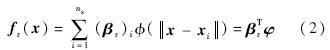
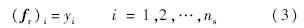
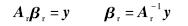
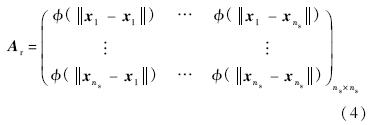
类BGM-109由二次曲线型弹头、圆柱形弹身、略收缩圆柱形弹尾、2副成一字型布局主翼(NACA64系列翼型)和4副成十字型布局尾翼组成[15].忽略进气道和助推器,创建的参数化类BGM-109模型与真实模型对比如图 6所示.
 |
| 图 6 类BGM-109模型与真实模型对比图Fig. 6 Quasi/real BGM-109 model geometry differences |
类BGM-109的气动计算工况为:马赫数0.7、攻角4.8°、飞行高度60 m.类BGM-109的隐身计算工况为:入射波频率450 MHz(参考美国“铺路爪”预警雷达的工作频率)、水平极化前向扫描、入射角90°~270°.其中,导弹模型的参考面积为1.114 8 m2,参考长度为0.52 m.
选取阻力系数Cd(初值为0.055)作为气动性能评价指标,选取前向RCS均值(用σ表示,初值为-10.859 dB·m2)作为隐身性能评价指标,根据期望与目标初值按均分原则划分的目标偏好如下所示:
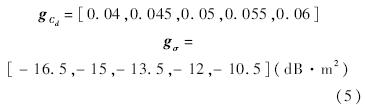
选取升力系数大于初始升力系数作为约束条件,导弹模型几何参数为设计变量(为保证导弹外形的拓扑关系不变,几何参数的变化范围选定在原尺寸的±20%),问题可用式(6)描述:
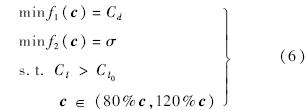
3.2 基于方差分析的变量筛选
采用Box-Behnken方法对式(6)所描述的问题进行采样(16维问题,共采取396个样本点),得到的重要度排序如表 1所示.综合考虑设计变量对偏好函数和约束条件的影响度大小,选取c3,c6,c8,c10和c13为筛选后的设计变量.筛选出的5个设计变量代表偏好函数的重要度之和为94.92%,代表约束条件的重要度之和为96.15%,能反映实际问题的基本情况.
| 设计变量 | 参数名称 | 重要度/% | |
| 偏好函数 | 约束条件 | ||
| c1 | 弹头长度 | 0.00 | 0.00 |
| c2 | 钝头半径 | 2.01 | 0.00 |
| c3 | 弹身直径 | 71.35 | 18.05 |
| c4 | 弹身长度 | 0.00 | 0.00 |
| c5 | 弹尾长度 | 0.00 | 0.00 |
| c6 | 尾部直径 | 10.62 | 1.83 |
| c7 | 主翼安装位置 | 1.00 | 0.00 |
| c8 | 主翼翼展 | 6.09 | 61.75 |
| c9 | 主翼根弦长 | 0.00 | 0.00 |
| c10 | 主翼稍弦长 | 1.40 | 7.89 |
| c11 | 主翼前缘后掠角 | 0.19 | 2.47 |
| c12 | 尾翼安装位置 | 0.49 | 0.00 |
| c13 | 尾翼翼展 | 5.46 | 6.63 |
| c14 | 尾翼根弦长 | 0.00 | 0.00 |
| c15 | 尾翼稍弦长 | 1.32 | 1.11 |
| c16 | 尾翼后缘后掠角 | 0.00 | 0.11 |
| 注:c3,c6,c8,c10和c13为筛选后的设计变量,加粗显示. | |||
优化流程(如图 7所示),可简述为以下6步: ①问题采样(用于变量筛选),并解算战术导弹气动隐身特性;②设置气动隐身综合偏好函数;③结合方差分析进行变量筛选;④对筛选后的问题进行采样,并解算战术导弹气动隐身特性;⑤构建代理模型并检验精度,若精度不满足要求则重复执行第⑤步;⑥将代理模型代入遗传算法进行优化,若结果满足设计要求则输出,反之则返回第②步.
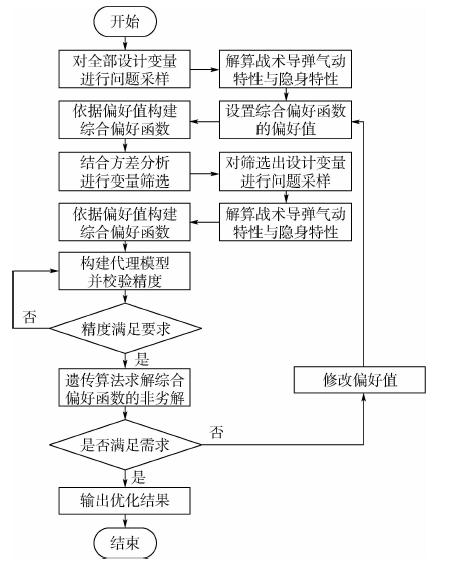 |
| 图 7 战术导弹气动隐身多目标优化流程Fig. 7 Flowchart of aerodynamic stealthy coupled multi-objective optimization for tactical missile |
考虑到DATCOM解算气动系数的平均耗时小于1 s,因此仅对较为耗时的隐身分析模型构建RBF代理模型.用拉丁超方试验设计方法采取220个样本点,随机选取200个样本点构造RBF代理模型,剩余的20个作为测试样本点.RBF为三次函数,代理模型的精度校验结果如表 2所示.相对误差均值为1.68%,复相关系数为0.943 4,代理模型的构造精度完全满足设计要求,即能很好地反映实际模型(入射波水平极化前向扫描的RCS均值)的真实情况.
利用物理规划构造类BGM-109气动隐身综合偏好函数,将综合偏好函数代入本文方法和标准遗传算法中,对类BGM-109的气动隐身性能进行有约束的多目标优化,优化结果与初始方案的比较如表 3、表 4及图 8所示.
| 方案 | Cd | σ/(dB·m2) | Cl | |
| 初始方案 | 初始数据 | 0.055 | -10.859 | 0.477 |
| 遗传算法 | 优化结果 | 0.046 | -15.946 | 0.481 |
| 变化量 | -16.4% | -46.8% | +1% | |
| 本文方法 | 优化结果 | 0.048 | -15.358 | 0.548 |
| 变化量 | -12.7% | -41.4% | +15.3% | |
| 项目 | c3 | c6 | c8 | c10 | c13 |
| 初值 | 0.520 | 0.240 | 1.055 | 0.300 | 0.270 |
| 最优值 | 0.416 | 0.192 | 1.266 | 0.320 | 0.284 |
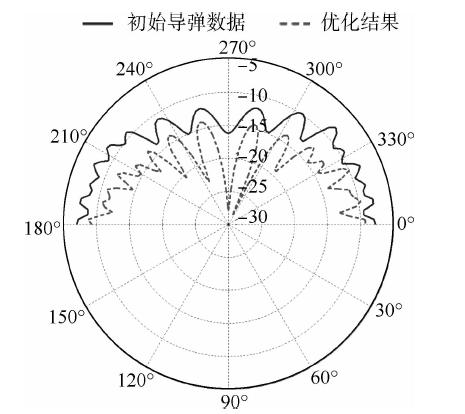 |
| 径向数据表征前向散射的RCS,dB·m2;周向数据表征入射角度. 图 8 RCS前向散射特性对比Fig. 8 Change of heading RCS |
在Intel(R)Xeon(R)X5570 2.93 GHz 8核计算机上本文方法优化耗时约12 h,标准遗传算法优化耗时约71 h.导弹阻力系数由0.055降为0.048(标准遗传算法为0.046),导弹水平极化前向扫描RCS(dB·m2)均值由-10.859降到-15.358(标准遗传算法为-15.946).在两者优化结果基本一致的情况下,节约了83%的计算成本.
4 结 论
本文将物理规划、变量筛选技术与GA相结合,提出了一种快速求解战术导弹气动隐身多目标优化问题的方法,经实例计算分析表明:
1) 经过变量筛选,设计者能直观地获得几何外形参数对气动隐身性能影响的重要度排序,即给出了改善气动隐身性能的努力方向;
2) 本文算法将参考模型的阻力系数降低了12.7%,前向RCS降低了41.4%,与遗传算法相比,在优化结果相差小于6%的情况下,减少了83%的计算量;
3) 筛选出的5个设计变量中有3个设计变量取到了边界值,可预计若适当放宽约束条件,得到的优化结果会更好.
为使本文方法在工程中得到运用,还应进行诸如蒙特卡洛试验等设计试验,使设计变量的取值范围更加合理.
| [1] | 彭瑾,徐兴柱,宋艳波,等.国外导弹隐身技术现状与发展趋势[J].飞航导弹,2009(3):23-27 Peng Jin,Xu Xingzhu,Song Yanbo,et al.The development of the abroad missile in stealthy technology[J].Aerodynamic Missile Journal,2009(3):23-27(in Chinese) |
| Cited By in Cnki (5) | |
| [2] | 戴全辉.一种隐身无人飞行器外形的电磁散射特性的实验研究[J].宇航学报,2001,22(1):65-69 Dai Quanhui.Expermental research on the electromagnetic scattering characteristics of stealthy UAV[J].Journal of Astronautics,2001,22(1):65-69(in Chinese) |
| Cited By in Cnki (3) | |
| [3] | 胡添元,余雄庆.基于参数化CAD模型的飞行器气动/隐身一体化设计[J].宇航学报,2009,30(1):123-127 Hu Tianyuan,Yu Xiongqing.Integrated design of aerodynamic and stealthy performance based on parametric CAD model[J].Journal of Astronautics,2009,30(1):123-127(in Chinese) |
| Cited By in Cnki (12) | |
| [4] | 廖炎平,刘莉,龙腾.基于多属性决策的气动隐身多目标优化[J].机械工程学报,2012,48(13):132-140 Liao Yanping,Liu Li,Long Teng.Multi-objective aerodynamic and stealthy performance optimization based on multi-attribute decision making[J].Journal of Mechanical Engineering,2012,48(13):132-140(in Chinese) |
| Cited By in Cnki (7) | |
| [5] | 张昆,薛晓春.截面形状与战术导弹隐身设计[J].战术导弹技术,2008(2):4-8 Zhang Kun,Xue Xiaochun.The shape of section and design of radar stealth of tactical missile[J].Tactical Missile Technology March,2008(2):4-8(in Chinese) |
| Cited By in Cnki | |
| [6] | 楚亮,马东立,刘忠铁.非圆截面弹体气动隐身一体化设计方法[J].北京航空航天大学学报,2009,35(10):1268-1272 Chu Liang,Ma Dongli,Liu Zhongtie.Integrated design of aerodynamic and stealthy performance for missiles with non-circular cross section[J].Journal of Beijing University of Aeronautics and Astronautics,2009,35(10):1268-1272(in Chinese) |
| Cited By in Cnki | |
| [7] | 刘莉,邢超,龙腾.基于物理规划的弹道多目标优化[J].北京理工大学学报,2013,33(4):357-362 Liu Li,Xing Chao,Long Teng.Study of multi-objective trajectory optimization based on physical programming[J].Transactions of Beijing Institute of Technology,2013,33(4):357-362(in Chinese) |
| Cited By in Cnki (1) | |
| [8] | Peng L,Liu L,Long T.Study of sequential radial basis function for computation-intensive design optimization problem[C]//12th AIAA Aviation Technology,Integration and Operations(ATIO)Conference and 14th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference.Reston,VA:AIAA,2012 |
| Click to display the text | |
| [9] | 龙腾,郭晓松,彭磊,等.基于信赖域的动态径向基函数代理模型优化策略[J].机械工程学报,2014,50(5):161-167 Long Teng,Guo Xiaosong,Peng Lei,et al.Optimization strategy using dynamic radial basis function metamodel based on trust region[J].Journal of Mechanical Engineering,2014,50(5):161-167(in Chinese) |
| Cited By in Cnki | |
| [10] | Blake W B.Missile datcom:user's manual[R].AFRL-VA-WP-TR-1998-3009,1998 |
| [11] | Blair Jr A B,Dillon J L,Watson C B.Experimental study of tail-span effects on a canard-controlled missile[J].Journal of Spacecraft and Rockets,1993,30(5):635-641 |
| Click to display the text | |
| [12] | Volakls J L,Woo A C,Wang H T G,et al.Benchmark radar targets for the validation of computational electromagnetics programs[J].IEEE Antennas and Propagation Magazine,1993,35(1):84-89 |
| Click to display the text | |
| [13] | Messac A.Physical programming:effective optimization for computational design[J].AIAA Journal,1996,34(1):149-158 |
| Click to display the text | |
| [14] | 龙腾.飞行器多学科设计优化方法与集成设计平台研究[D].北京:北京理工大学,2009 Long Teng.Research on methods of multidisciplinary design optimization and integrated design[D].Beijing:Beijing Institute of Technology,2009(in Chinese) |
| [15] | Craig R E,Reich R J.Flight test aerodynamic drag characteristics development and assessment of in-flight propulsion analysis methods for the AGM-109 cruise missile[C]//1st Flight Test Conference.New York:AIAA,1981 |


