现代飞行器具有大柔性的特点,飞行时在升力方向产生变形的同时也在展向产生一定变形.较大的弹性变形会引起气动力产生不可忽略的损失[1].为了满足现代飞行器气动弹性计算的精度要求,基于计算流体力学(CFD)/计算结构力学(CSD)的耦合仿真方法正逐步取代基于小变形假设的结构分析方法和传统的升力面气动力计算方法,并逐渐成为主要研究手段[2].
气动弹性CFD/CSD耦合计算涉及气动和结构两套网格,一般而言,两套网格在飞行器表面是不一致的.气动网格要求在气动力变化较大的部位布置密网格,如机翼的前、后缘和翼尖等处,因而气动网格能够很好地体现飞行器的曲面外形.而结构力学分析则基于传力特性进行力学简化,较多采用一些梁、壳等单元以便进行力学分析,此时已不能够准确反应飞行器的曲面外形.尤其是当结构模型为梁模型时,已经不存在曲面外形.因而要实现气动/结构的耦合计算,需要很好地处理两套网格之间的数据传递问题.Harder[3]等人提出了无限平板样条方法(IPS),并得到广泛应用[4, 5].常体积转换法(CVT)方法[6]通过保持气动点与结构点组成的四面体体积守恒来完成的流/固耦合的位移插值[7].近年来,以径向基函数(RBF)方法[8]及其改进的方法[9]为基础的插值方法逐渐用于气动弹性的数据插值中并取得了令人满意的结果[10, 11].然而,当数据从固体到流体插值时,需要选取适当的结构模型样本点建立结构模型网格到流体网格的映射关系;当数据从流体到结构插值时,需要选取适当的流体样本点建立流体网格到结构模型网格的映射关系.显然,分别建立流体/固体之间的映射关系增加了CFD/CSD耦合计算的复杂度.
本文将自主研发的N-S方程计算程序与大型通用有限元软件NASTRAN耦合[12],开展某机翼静气动弹性CFD/CSD计算分析.同时简化气动/结构的双向映射过程,采用MPC方法[13]建立气动/结构的双向数据传递.构建结构单元到机翼表面气动点的MPC,实现结构模型到气动表面网格的映射关系.有限元方法计算结构变形,通过MPC方法插值出气动表面点的变形,利用基于扰动衰减规律的弹性变形技术快速生成变形网格.CFD计算弹性机翼气动表面点的节点力,通过所建立的MPC,采用虚功原理将气动点的节点力传递到结构有限元模型上,进行下一轮有限元计算.MPC的变形插值和节点力传递可由NASTRAN软件计算,因此本文方法可以快捷地实现现有CFD求解器与NASTRAN软件的耦合计算.由于插值过程与NASTRAN求解序列无关,因而可以快捷地实现结构线性/非线性的静气动弹性计算分析.
1 气动力与结构变形计算 1.1 定常气动力N-S方程计算
采用有限体积法求解三维N-S方程:
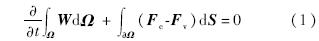
采用Runge-Kutta显式方法对式(1)进行时间推进.基于雷诺平均N-S方程模拟紊流,紊流模型选用S-A一方程模型.利用块结构网格并行技术提高计算效率[14],基于分块网格的基本块分配计算任务,计算区域的划分尽量满足负载平衡和通讯量最少化这两个基本要求.
1.2 结构变形计算
采用有限元方法计算结构变形.应用NASTRAN进行某大展弦比机翼结构有限元建模,其中结构模型为考虑弯曲和扭转的梁模型.CFD计算的气动力以节点力的形式通过MPC加载到有限元模型上,进而提交NASTRAN求解.NASTRAN线性101求解器求解线性静力学方程:

对于柔度法,求解刚度矩阵的逆矩阵,采用IPS插值方法得到机翼表面气动网格单元的柔度矩阵C,求解静力学方程:
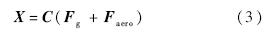
NASTRAN非线性106求解序列则求解考虑几何大变形和跟随力的非线性静力学方程[15].
2 流/固耦合双向数据传递MPC方法
为了实现流场与结构场之间的双向数据传递,针对每一个气动表面点搜寻距离其最近的机翼主梁单元,构建气动点到结构梁单元的MPC,如图 1所示.
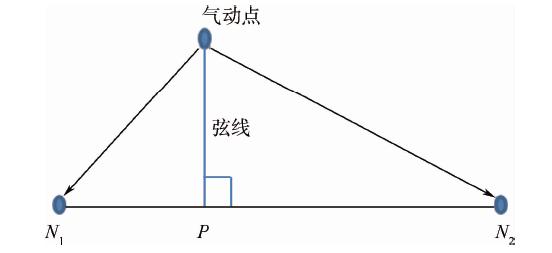 |
| 图 1 梁单元的多点约束Fig. 1 MPC of a beam element |
机翼表面气动网格点的气动载荷以节点力的形式通过虚功原理加载到结构单元用于结构有限元分析.通过有限元分析计算得到节点N1和N2的位移.假设节点Ni的平动、转动位移向量分别为Ti和Ri,气动点相对于N1和N2点的初始位置向量为r1和r2.关联气动点的3个平动自由度到N1和N2点3个平动自由度和3个转动自由度上.则当N1点产生了位移时,由N1点引起的气动点位移为
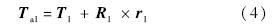
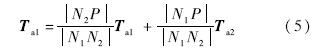
对于复杂有限元模型,一般而言飞行器具有蒙皮结构,因而需要构建气动点到蒙皮的多点约束.简化蒙皮为二维的壳单元,构建气动点到二维单元的MPC.以四边形单元为例,搜寻距离气动点最近的四边形单元,构建点到单元的映射关系如图 2所示.
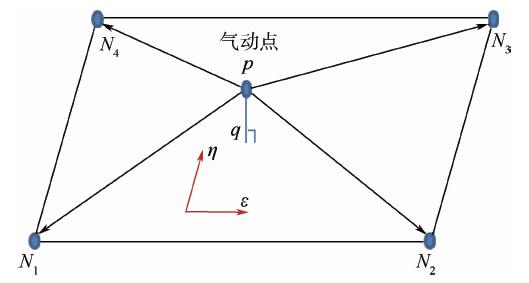 |
| 图 2 四边形单元的多点约束Fig. 2 MPC of a quadrilateral element |
投影气动点p到结构单元内于q点,则q点在单元内的二维参数坐标为(ε,η).通过式(6)中四边形等参单元的形函数可以计算出q点在四边形内的插值系数N1~N[16]4:
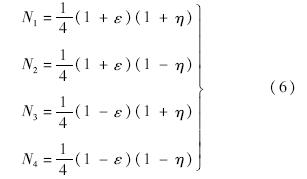

类似文献[14]的柔度法,采用定常气动力和结构变形交替迭代的静气动弹性计算方法.定常气动力采用自主研发的N-S方程求解器计算,结构变形采用有限元方法计算,并利用MPC方法完成流/固耦合双向数据传递,考虑结构几何非线性,建立CFD/NASTRAN耦合的大展弦比机翼静气动弹性数值计算方法.显然,文献[14]提出的保持结构收敛过程与气动收敛过程同步进行的紧耦合迭代方法也适用于CFD/NASTRAN耦合的静气动弹性计算分析,具体计算流程如下:
1) 构建结构模型,划分气动网格,设定计算状态参数;
2) 提取所有气动表面网格点,构建气动点到结构单元的MPC,生成NASTRAN线性101/非线性106求解序列的BDF文件;
3) N-S方程计算机翼气动表面点的节点力;
4) 通过MPC,采用虚功原理将气动节点力加载到结构有限元模型,利用NASTRAN线性或非线性求解序列进行结构计算;
5) 结构计算得到结构点位移,通过MPC计算得到气动表面点的位移,利用弹性变形技术生成新的气动网格;
6) 重复步骤3)~5),直至收敛,得到给定迎角α、马赫数Ma、雷诺数Re、速压Q下考虑弹性影响的气动特性.
4 计算结果及讨论
分别采用CFD/柔度法、CFD/NASTRAN线性求解器、CFD/NASTRAN非线性求解器耦合的方法计算某大展弦比机翼静气动弹性,其中耦合柔度法采用IPS插值方法,耦合NASTRAN采用本文的MPC插值方法.计算状态为马赫数Ma=0.785、迎角α=2.465°、飞行高度H=11.28 km.柔度法采用只考虑纵向变形的传统计算方法,NASTRAN非线性求解序列考虑几何非线性影响,以此分析展向变形和几何非线性对其静气动弹性特性的影响.
利用Gridgen软件生成机翼的分块结构网格.图 3给出了机翼的气动表面网格.
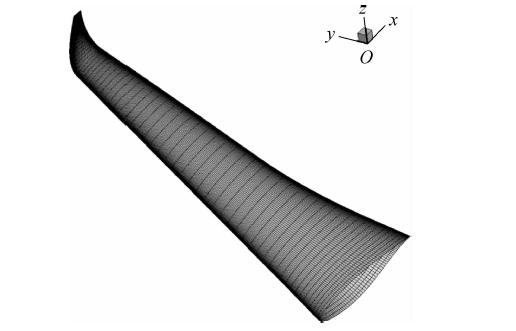 |
| 图 3 机翼表面的气动网格Fig. 3 Aerodynamic grids of the wing surface |
结构模型为考虑弯曲刚度和扭转刚度的梁模型,质量部分考虑机翼以及吊舱质量,结构模型如图 4所示.
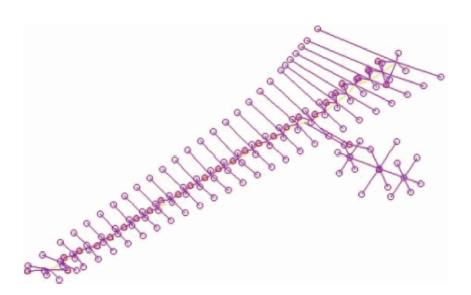 |
| 图 4 机翼的有限元模型Fig. 4 Finite element model of the wing |
柔度法计算静气动弹性问题时需要机翼表面气动网格单元的柔度阵,采用辅助单元将机翼梁模型的柔度插值到机翼平面上,见图 5.继而采用IPS方法插值到机翼表面气动网格.柔度法计算时采用IPS插值法只进行一次柔度插值,插值后气动力和变形计算均在气动网格上进行.
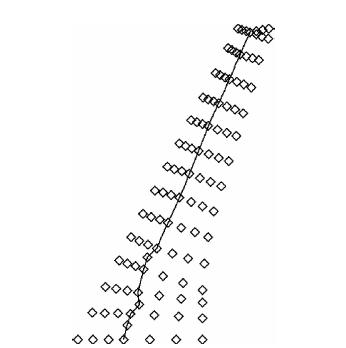 |
| 图 5 柔度矩阵插值点分布Fig. 5 Point distribution of flexibility method |
采用多点约束计算静气动弹性问题时需要构建气动点到结构模型的多点约束,图 6、图 7分别给出了翼型截面上的气动点到结构点的多点约束和机翼气动表面点到结构单元的多点约束.
 |
| 图 6 翼型截面多点约束Fig. 6 MPC of a airfoil section |
 |
| 图 7 机翼表面的多点约束Fig. 7 MPC of the wing surface |
CFD/柔度法、CFD/NASTRAN耦合计算得到的机翼静平衡构型比较如图 8所示,图 9进一步给出了翼尖处的变形图.其中红色为没有发生结构变形的初始外形,蓝色、绿色和灰色分别代表柔度法、NASTRAN线性和非线性求解器计算的静平衡构型.图 8表明在翼根处变形很小,柔度法与NASTRAN线性、非线性求解器计算的静平衡构型有重叠区域.图 9表明在翼尖处NASTRAN线性、非线性求解器计算的静平衡构型基本重合,几何非线性影响很小;而NASTRAN线性求解序列与只考虑纵向z方向的柔度法的静平衡构型存在一定差异.
 |
| 图 8 柔度法和有限元法计算的机翼静平衡构型比较Fig. 8 Static aeroelastic sharp comparison of the flexibility and the FEM method |
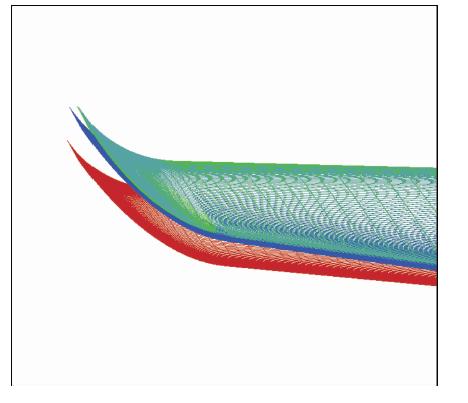 |
| 图 9 柔度法和有限元法计算的翼尖变形比较Fig. 9 Wing tip deformation comparison of the flexibility and the FEM method |
图 10~图 12进一步对比了CFD/柔度法、CFD/NASTRAN耦合计算得到的机翼前缘处纵向z方向、展向y方向的变形和扭角分布.图 10表明柔度法和NASTRAN线性、非线性求解器计算的纵向变形相吻合.图 11表明NASTRAN结果带有展向变形,非线性求解序列由于考虑了跟随力效应其展向变形较线性结果大;柔度法只采用了z方向柔度,没有展向变形,因而图 9中NASTRAN与柔度法的静平衡构型间的差别主要来自于展向变形.图 12表明NASTRAN线性、非线性求解器的扭角分布结果差异甚小;柔度法与NASTRAN结果走势相同,但NASTRAN计算的扭角较大,其中NASTRAN线性求解器计算的最大扭角为2.702°,柔度法为2.607°,相差3.5%;在展向坐标4 m处,由于在将机翼梁模型的柔度插值到机翼平面过程中采用了光滑的插值方法,故柔度法结果未能很好地体现出扭角的不光滑性.
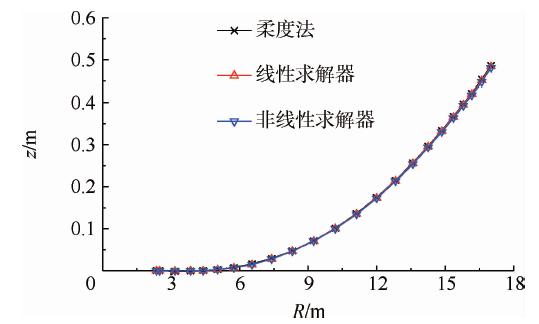 |
| 图 10 机翼z方向变形比较Fig. 10 Deformation distribution of the wing in z direction |
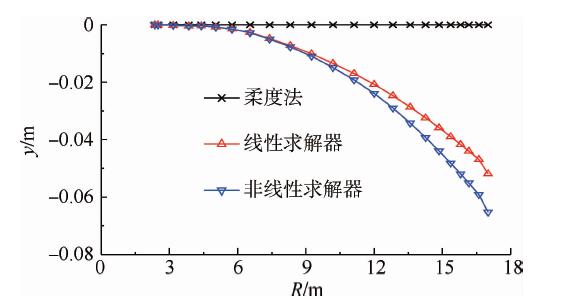 |
| 图 11 机翼y方向变形比较Fig. 11 Deformation distribution of the wing in y direction |
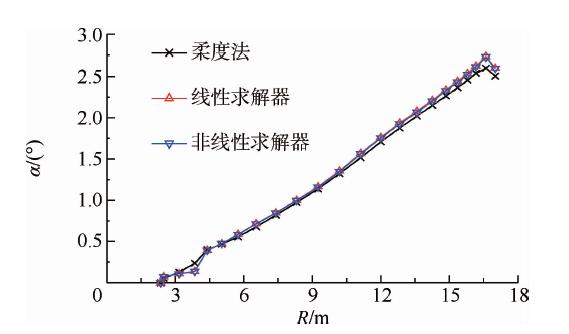 |
| 图 12 机翼扭角分布比较Fig. 12 Torsion angle distribution of the wing |
表 1给出了CFD/柔度法和CFD/NASTRAN耦合计算得到的升阻力系数对比.耦合NASTRAN线性、非线性求解器计算的升阻力系数相差均在1‰左右,相差很小.而柔度法相对于耦合NASTRAN线性求解器的升力系数相差1.38%,阻力系数相差0.47%.柔度法计算出的升阻力系数均相对较大,这是由于本文柔度法计算只考虑纵向变形而忽略展向变形,致使弹性变形后的机翼面积相对较大,而本文CFD/NASTRAN耦合计算方法更能体现机翼的真实弹性变形,结果更为可靠.
| 计算方法 | 升力系数 | 阻力系数 |
| 柔度法 | 0.463 3 | 0.012 85 |
| NASTRAN线性求解器 | 0.457 0 | 0.012 79 |
| NASTRAN非线性求解器 | 0.456 5 | 0.012 78 |
本文建立的基于多点约束插值方法对某单梁结构机翼进行静气动弹性计算分析,结果表明:
1) MPC流固耦合数据交换方法只需建立气动点到结构单元的映射关系.部分MPC插值计算可以由NASTRAN完成且与Bdf文件内的求解序列无关,因而可以快速方便地与NASTRAN软件的线性、非线性求解器进行耦合计算.
2) 机翼变形只考虑升力方向会使机翼面积有所增大,使得气动力在一定程度上产生偏差.飞行器气动弹性计算时需要精确考虑三维变形.
3) 本文算例巡航状态的升力方向翼尖变形量只有半展长3%左右,几何非线性对机翼的变形以及气动力的影响较小,可以忽略不计.
| [1] | 马铁林,马东立,张华.大展弦比柔性机翼气动特性分析[J].北京航空航天大学学报,2007,33(7):781-784 Ma Tielin,Ma Dongli,Zhang Hua.Aerodynamic characteristic analysis of high-aspect ratio elastic wing[J].Journal of Beijing University of Aeronautics and Astronautics,2007,33(7):781-784(in Chinese) |
| Cited By in Cnki (14) | Click to display the text | |
| [2] | 谢亮,徐敏,安效民,等.基于径向基函数的网格变形及非线性气动弹性时域仿真研究[J].航空学报,2013,34(7):1501-1511 Xie Liang,Xu Min,An Xiaomin,et al.Research of mesh deforming method based on radial basis functions and nonlinear aeroelastic simulation[J].Acta Aeronautica et Astronautica Sinica,2013,34(7):1501-1511(in Chinese) |
| Cited By in Cnki (2) | |
| [3] | Harder R L,Desmarais R N.Interpolation using surface splines[J].Journal of Aircraft,1972,9(2):189-191 |
| Click to display the text | |
| [4] | Liu F,Cai J,Zhu Y,et al.Calculation of wing flutter by a coupled fluid-structure method[J].Journal of Aircraft,2001,38(2):334-342 |
| Click to display the text | |
| [5] | Smith M J,Hodges D H.Evaluation of computational algorithms suitable for fluid-structure interactions[J].Journal of Aircraft,2000,37(2):282-294 |
| Click to display the text | |
| [6] | Goura G S L,Badcock K J,Woodgate M A,et al.A data exchange method for fluid-structure interaction problems[J].Aeronautical Journal,2001,105(1046):215-221 |
| Click to display the text | |
| [7] | 徐敏,陈士橹.CFD/CSD耦合计算研究[J].应用力学学报,2003,21(2):33-36 Xu Min,Chen Shilu.Study of date exchange method for coupling computational CFD/CSD[J].Chinese Journal of Applied Mechanics,2003,21(2):33-36(in Chinese) |
| Cited By in Cnki (51) | Click to display the text | |
| [8] | Wendland H.Computational aspects of radial basis function approximation[J].Studies in Computational Mathematics,2006,12:231-256 |
| Click to display the text | |
| [9] | Wendland H.Piecewise polynomial,positive definite an compactly supported radial basis functions of minimal degree[J].Adv Comput Math,1995,4:389 |
| Click to display the text | |
| [10] | Frank R.Scattered data interpolation:tests of some methods[J].Math Comp,1982,38:191 |
| Click to display the text | |
| [11] | 杨国伟,郑冠男.基于静气动弹性效应的飞机型架外形修正方法研究[J].航空工程进展,2011,2(2):143-150 Yang Guowei,Zheng Guannan.Aircraft jig shape correction method based on static aeroelastic analyses[J].Advances in Aeronautical Science and Engineering,2011,2(2):143-150(in Chinese) |
| Cited By in Cnki (1) | |
| [12] | 林言中,陈兵,徐旭.基于径向基函数插值的气动弹性计算方法[J].北京航空航天大学学报,2013,39(1):1-7 Lin Yanzhong,Chen Bing,Xu Xu.Numerical method of aeroelasticity based on radial basis function interpolation[J].Journal of Beijing University of Aeronautics and Astronautics,2013,39(1):1-7(in Chinese) |
| Cited By in Cnki | Click to display the text | |
| [13] | 曲晓锐,钱才富.多点约束(MPC)法与换热器整体有限元分析[J].压力容器,2013,30(2):54-58 Qu Xiaorui,Qian Caifu.Multipoint constrain method and finite element analysis of whole heat echangers[J].Pressure Vessel Technology,2013,30(2):54-58(in Chinese) |
| Cited By in Cnki (3) | Click to display the text | |
| [14] | Huang W,Lu Z L,Guo T Q,et al.Numerical method of static aeroelastic correction and jig-shape design for large airliners[J].Science China,2012,55(9):2447-2452 |
| Click to display the text | |
| [15] | 谢长川,吴志刚,杨超.大展弦比柔性机翼的气动弹性分析[J].北京航空航天大学学报,2003,29(12):1087-1090 Xie Changchuan,Wu Zhigang,Yang Chao.Aeroelastic analysis of flexible large aspect ratio wing[J].Journal of Beijing University of Aeronautics and Astronautics,2003,29(12):1087-1090(in Chinese) |
| Cited By in Cnki | |
| [16] | 徐敏,史志军,陈士橹.一种流体-结构耦合计算问题的网格数据交换方法[J].西北工业大学学报,2003,21(5):532-535 Xu Min,Shi Zhijun,Chen Shilu.A suitable method for transferring information between CFD and CSD grids[J].Journal of Northwestern Poly Technical University,2003,21(5):532-535(in Chinese) |
| Cited By in Cnki (38) | Click to display the text |




