当今战场环境复杂多变,电磁环境愈发复杂,采用单一传感器信息对导弹进行制导必然面临探测不精确、易受敌欺骗干扰、目标信息易中断等问题[1],因此采用网络瞄准,将多源信息进行融合,为导弹提供制导信息从而实现网络化制导成为未来信息化战争的必然选择[2].在对多源信息进行融合的过程中,由于传感器探测存在系统误差、传感器平台自身定位误差以及定姿误差等因素,需要进行空间配准处理[3],以提高数据融合精度.当只有一种误差被估计时,通常可以得到满意的估计性能,而涉及两种或两种以上误差源的结果由于解耦问题都得不到满意的结果.
现有空间配准算法可以简单地分为两类,即离线空间配准与在线空间配准.离线空间配准算法主要基于最小二乘算法和最大似然算法;在线空间配准算法主要基于滤波算法[4].导弹的制导过程对实时性要求较强,因此网络瞄准环境下的空间配准算法应采用在线空间配准算法.在线空间配准算法分为两类[5],一类是Nabaa和Bishop在文献[6]中提出的基于扩展卡尔曼滤波(EKF，Extend Kalman Filter)的扩展状态向量空间配准算法,将目标的状态与传感器的误差合成一个扩展状态向量进行估计;但此算法由于状态向量维数较大,因此存在计算量较大的问题,针对此问题,文献[7]讨论了两级滤波算法,但只有在特定条件下才发挥作用,因此实时性仍然难以保证.另一类是基于地心地固(ECEF,Earth Fixed Earth Center)坐标系的伪量测算法[8],此类算法相对扩展状态向量法具有运算量小的优点.但是无论以上哪种算法,均以传感器量测数据的时间同步为前提,异步传感器的空间配准算法研究较少.文献[9, 10]均对异步空间配准算法进行了深入研究.其中比较有代表性的为文献[9]中提出的将时间分片,并将时间片内数据率较高的传感器的量测数据通过线性加权得到与数据率较低的传感器数据率相同的量测数据,由此得到与目标状态无关的伪量测.文献[10]也是考虑对多个量测进行加权以实现量测同步,加权系数的确定以伪量测与目标状态无关为准则,但是以上两种算法都是以目标作匀速直线运动为假设基础,若目标作非匀速直线运动,则由上述方法构建的伪量测依然与目标的运动状态有关,且文中算法并未对此问题进行深入考虑.
本文算法首先采用内插外推时间配准算法对各量测进行时间配准,随后采用基于ECEF的在线空间配准算法,证明了内插外推时间配准后的量测在计算伪量测时也与目标状态无关.根据得到的伪量测,结合卡尔曼滤波即可实现在线的异步空间配准,对传感器的系统误差进行估计.
1 基于伪量测的同步空间配准算法 1.1 量测模型假设k时刻目标在本地直角坐标系下真实位置为X′1(k)=[x′1(k),y′1(k),z′1(k)]T,极坐标系下对应的量测值为[r(k),θ(k),φ(k)],转换至本地直角坐标系下为X1(k)=[x1(k),y1(k),z1(k)]T.传感器系统偏差为ξ(k)=[Δr(k),Δθ(k),Δφ(k)]T,于是有
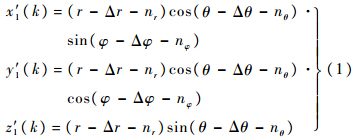
式(1)可以用一阶近似展开并写成矩阵形式：
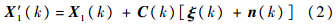
设两部传感器A和B,则对于同一个公共目标(设地心地固坐标系下为X′e=[x′e,y′e,z′e]T),可得[8, 9, 10, 11]
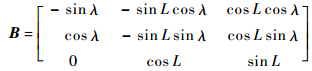
定义伪量测为
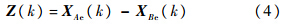
将式(2)、式(3)代入式(4)可以得到关于传感器偏差的伪测量方程:
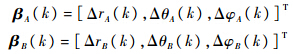
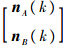,为测量噪声.由于nA(k),nB(k)为零均值、相互独立的高斯型随机变量,其噪声协方差矩阵分别为RA(k),RB(k),则O(k)同样是零均值高斯型随机变量,其协方差矩阵为
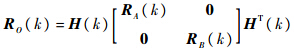
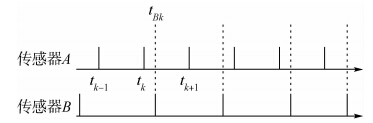
时间配准算法主要有内插外推法[12]、最小二乘法[13]、曲线拟合法[14].其中内插外推法和最小二乘法均为加权算法,但是最小二乘法的推导过程基于目标作匀速运动,所以采用内插外推法进行时间配准.假设传感器A、传感器B在本地直角坐标系下的量测数据分别为YA(ti)和YB(ti),且传感器A的采样频率大于传感器B的采样频率,则由传感器A向传感器B的采样时刻进行配准,如图 1所示.
 |
| 图 1 内插外推时间配准算法Fig. 1 Algorithm of interpolation time registration |
内插外推时间配准算法的原理是[12]:在同一时间片内将各传感器观测数据按测量精度进行增量排序,然后将传感器A的观测数据分别向传感器B的时间点内插、外推,以形成一系列等间隔的目标观测数据,采用常用的三点抛物线插值法进行内插外推时间配准算法可得传感器A在tBk时刻在本地直角坐标系下的量测值为
YA(tk－1),YA(tk),YA(tk+1)分别为传感器A对目标在tk－1,tk,tk+1时刻的本地笛卡儿坐标系下的量测值,分别为
将式(7)~式(9)代入式(6),可得
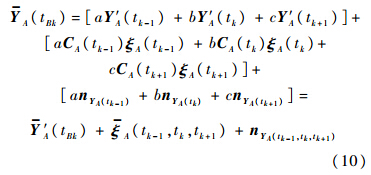
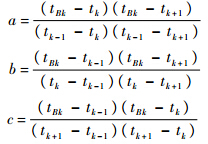
而tBk时刻,传感器B的量测为
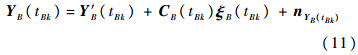
根据基于ECEF的空间配准算法,定义伪量测为
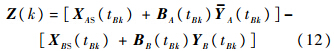
对于同一公共目标,其在ECEF坐标系下的位置为Xe则有
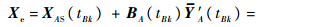
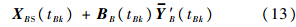
将式(11)、式(13)代入式(12),则有
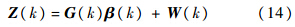
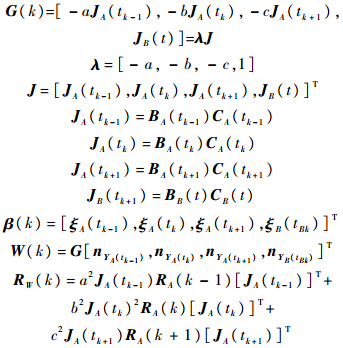
由式(14)可以看出,由此方法构建的伪量测仅与传感器的位置、传感器的量测值、传感器的数据时间、传感器的系统误差、传感器的随机噪声相关,而与目标的状态信息无关.因此利用内插外推时间配准后的传感器数据进行空间配准的方法是可行的.
可以得到传感器系统误差的状态方程和量测方程:
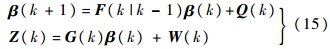
根据式(15)构建的伪量测方程采用卡尔曼滤波进行递推,即可得到传感器的系统误差.
首先进行一步预测:
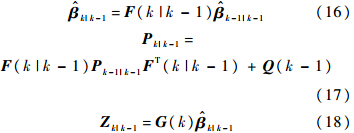
随后计算滤波增益:
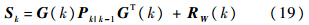
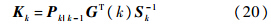
最后完成更新:
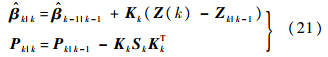
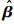k|k即为传感器的量测系统误差估计.
2.3 算法步骤根据前文分析,本文提出的异步传感器空间配准算法步骤如下:
1) 确定低采样率传感器的数据时刻(如前文中的传感器B的数据时刻tBk);
2) 采用内插外推时间配准算法,根据式(6)计算高采样率传感器的时间配准结果;
3) 根据式(12)计算伪量测方程.
采用卡尔曼滤波,根据式(16)~式(21)估计传感器的系统误差.
3 仿真分析假定传感器A的系统误差为ξA(k)=[100 m,0.01 rad,0.01 rad]T,随机噪声为均值为0、协方差为diag[102,0.0022,0.0022]的白噪声,采样周期为0.08 s.传感器B的系统误差为ξB(k)=[－150 m,0.05 rad,－0.02 rad]T,随机噪声为均值为0、协方差为diag[102,0.0022,0.0022]的白噪声,采样周期为0.1 s.传感器A在ECEF坐标系下的位置为(0,0,0),传感器B在ECEF坐标系下的位置为(10 000,10 000,5 000).目标在ECEF坐标系下的初始位置为(5 000,5 000,2 000).
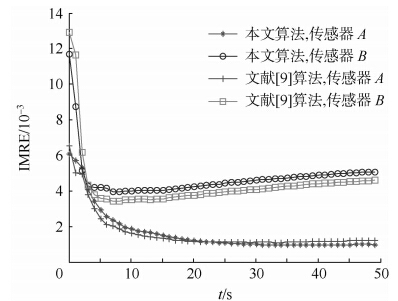
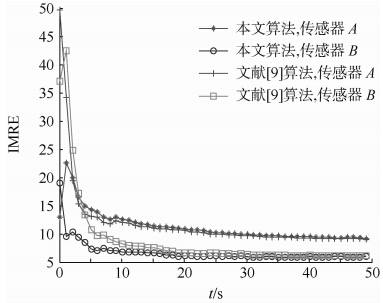
3.1 目标匀速直线运动假定目标尚未发现被导弹锁定,仍然保持匀速直线运动状态,速度为[100 m/s,200 m/s,10 m/s].分别采用本文算法和文献[9]中的算法对传感器的系统误差进行估计,结果如图 2~图 4所示.此处所采用的评价方式为迭代中值误差(IMRE，Interative Mid-Range Error)[15],可避免均方根误差(RMSE，Root Mean Square Error)在结果评估中的悲观性,且具有较好的鲁棒性.
 |
| 图 2 匀速条件下距离误差估计IMREFig. 2 IMRE of range bias estimation with CV motion |
 |
| 图 3 匀速条件下方位角误差估计IMREFig. 3 IMRE of azimuth bias estimation with CV motion |
 |
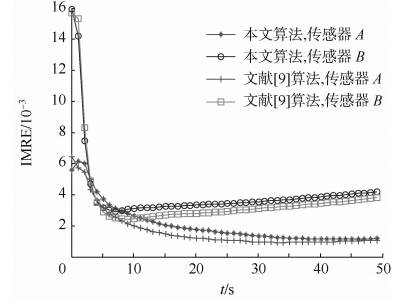| 图 4 匀速条件下俯仰角误差估计IMREFig. 4 IMRE of elevation bias estimation with CV motion |
由图 2~图 4可以发现,当目标匀速运动时,本文算法对传感器的系统误差估计的IMRE和文献[9]中的算法对传感器的系统误差估计的IMRE相差不大.传感器A的距离系统误差的估计精度在10 m左右,传感器B的距离系统误差的估计精度在3 m左右;传感器A的方位角系统误差的估计精度在0.002 rad左右,传感器B的方位角系统误差的估计精度在0.004 rad左右;传感器A的俯仰角系统误差的估计精度在0.002 rad左右,传感器B的俯仰角系统误差的估计精度在0.004 rad左右.
3.2 目标蛇形机动假定目标发现被锁定,立即采取蛇形机动,现分别采用本文算法和文献[9]中算法对传感器的系统误差进行估计,结果如图 5~图 7所示.
 |
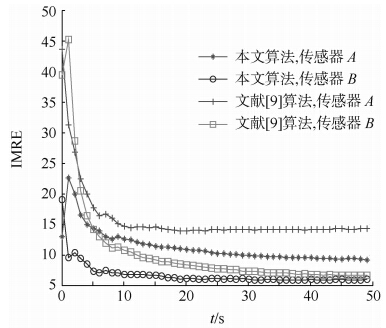| 图 5 机动条件下距离误差估计IMREFig. 5 IMRE of range bias estimation with snake-maneuver motion |
 |
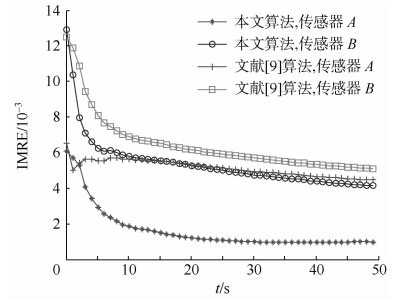| 图 6 机动条件下方位角误差估计IMREFig. 6 IMRE of azimuth bias estimation with snake-maneuver motion |
 |
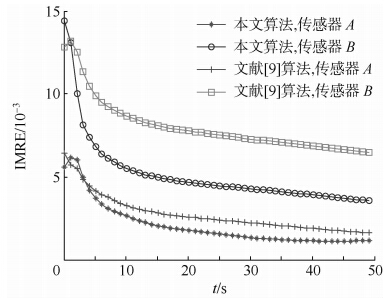| 图 7 机动条件下俯仰角误差估计IMREFig. 7 IMRE of elevation bias estimation with snake-maneuver motion |
由图 5~图 7可以看出,当目标作蛇形机动时,本文算法受影响很小,仍然可以较好地估计传感器的系统误差,但文献[9]算法的估计精度略有下降.本文算法对传感器距离误差的估计精度仍然能维持在10 m以下,但文献[9]中算法对传感器A的距离误差的估计精度已经恶化到15 m左右;在方位角和俯仰角系统误差的估计精度上,本文算法和文献[9]中的算法均有所恶化,但文献[9]中的算法明显受目标机动影响较大.
这是由于文献[9]的算法在在伪量测推导过程与目标的状态向量密切相关,且状态向量为位置和速度分量,因此难以抵抗目标机动可带来的误差.而本文的伪量测推到过程完全基于传感器对目标的量测,仅与目标的位置相关,并不受目标运动状态影响,因此在目标蛇形机动时,本文算法仍然可以较好地实现空间配准.
3.3 算法实时性验证导弹攻击目标的过程瞬息万变,因此需验证本文算法的实时性是否满足需求.本文算法在进行估计时状态向量的维数较文献[9]增加3维,因此滤波时间应稍有增加.本文仿真环境中的计算机配置如下,CPU为i3-2120,主频3.30 GHz,内存2 GB.在进行500步滤波的情况下,本文算法总的滤波时间需消耗0.008 2 s，文献[9]需消耗 0.007 8 s,本文算法仅增加 0.000 5 s,可认为未增加实时性负担.
4 结 论本文将内插外推时间配准算法应用于异步传感器空间配准算法中,推导了在此情况下的伪量测方程,实现了非同步传感器空间配准.本文算法的优越性在于推导伪量测方程的过程中未利用目标运动状态进行外推,从而减轻了目标的机动对伪量测方程的影响.仿真表明:本文算法在目标蛇形机动与非机动时均能实现对传感器系统误差的准确估计;算法实时性满足要求.但是,本文算法的局限性在于仍然只考虑了传感器的探测系统误差,定姿误差与定位误差都未考虑.
| [1] | 孙松斌,宋建梅,张婧.超低空拦截导弹武器系统的UKF-IMM目标跟踪算法[J].系统工程与电子技术,2009,31(10):2367-2371 Sun Songbin,Song Jianmei,Zhang Jing.Target tracking algorithm of super-low altitude interceptors based on UKF-IMM[J].Systems Engineering and Electronics,2009,31(10):2367-2371(in Chinese) |
| Cited By in Cnki (9) | Click to display the text | |
| [2] | 王琳,于雷,王小强,等.网络瞄准环境下最优分布式航迹融合算法[J].系统工程与电子技术,2011,33(11):2517-2521 Wang Lin,Yu Lei,Wang Xiaoqiang,et al.Optimal distributed track fusion method in network targeting[J].Control Theory and Applications,2011,33(11):2517-2521(in Chinese) |
| Cited By in Cnki (0) | Click to display the text | |
| [3] | Besada J A,de Miguel G,Bernardos A M,et al.Generic multisensor multitarget bias estimation architecture[J].IET Radar Sonar and Navigation,2012,6(5):365-378 |
| Click to display the text | |
| [4] | Besada P J A,García H J,De Miguel V G.New approach to online optimal estimation of multisensor biases[J].IEE Proceedings:Radar,Sonar and Navigation,2004,151(1):31-40 |
| Click to display the text | |
| [5] | Ristic B E,Gordon N.Calibration of multi-target tracking algorithms using non-cooperative targets[J].IEEE Journal of Selected Topics in Signal Processing,2013,7(3):390-398 |
| Click to display the text | |
| [6] | Nabaa N,Bishop R H.Solution to a multisensor tracking problem with sensor registration errors[J].IEEE Transactions on Aerospace and Electronic Systems,1999,35(1):354-363 |
| Click to display the text | |
| [7] | Hsieh C S.General two-stage extended Kalman filters[J].IEEE Transactions on Automatic Control,2003,48(2):289-293 |
| Click to display the text | |
| [8] | 李达,李少洪.基于地心坐标系的多传感器动态偏差估计算法[J].北京航空航天大学学报,2007,33(9):1082-1085 Li Da,Li Shaohong.Multisensor dynamic bias estimation with earth-centered earth-fixed coordinate system[J].Journal of Beijing University of Aeronautics and Astronautics,2007,33(9):1082-1085(in Chinese) |
| Cited By in Cnki (1) | |
| [9] | Lin X,Bar-Shalom Y,Kirubarajan T.Multisensor-multitarget bias estimation for general asynchronous sensors[J].IEEE Transactions on Aerospace and Electronic Systems,2005,41(3):899-921 |
| Click to display the text | |
| [10] | Hu Y Y,Zhou D H. Bias fusion estimation for multi-target tracking systems with multiple asynchronous sensors[J].Aerospace Science and Technology,2013,27(1):95-104 |
| Click to display the text | |
| [11] | Ristic B,Okello N.Sensor registration in ECEF coordinates using the MLR algorithm[C]//Proceedings of the 6th International Conference on Information Fusion,FUSION 2003.Cairns:IEEE Computer Society,2003,1:135-142 |
| Click to display the text | |
| [12] | Yang W J,Cui F,Li X,et al.Research on time registration algorithms of multi-sensor fusion system[C]//Proceedings of the Conference on Computer Science and Automation Engineering,2011:446-449 |
| Click to display the text | |
| [13] | 王宝树,李芳社.基于数据融合技术的多目标跟踪算法研究[J].西安电子科技大学学报,1998,25(3):269-272 Wang Baoshu,Li Fangshe.The research on multiple targets tracking based on the data fusion technique[J].Journal of Xidian University,1998,25(3):269-272(in Chinese) |
| Cited By in Cnki (89) | |
| [14] | 梁凯,潘泉,宋国明,等.基于曲线拟合的多传感器时间对准方法研究[J].火力与指挥控制,2006,31(12):51-53 Liang Kai,Pan Quan,Song Guoming,et al.The study of multi-sensor time registration method based on curve fitting[J].Fire Control and Command Control,2006,31(12):51-53(in Chinese) |
| Cited By in Cnki (18) | |
| [15] | Yin H L,Lan J,Li X R.New robust metrics of central tendency for estimation performance evaluation[C]//15th International Conference on Information Fusion,FUSION 2012.Washington D C:IEEE Computer Society,2012:2020-2027 |
| Click to display the text |
