表1(Table 1)
随着计算机技术的飞速发展,数值模拟方法在湍流研究中起到越来越重要的作用.其中,RANS/LES混合方法对传统RANS(Reynolds Averaged Navier-Stokes)方法感到棘手的大尺度分离问题特别有效,其网格需求量远小于理想的LES(Large Eddy Simulation)方法,仅略大于三维的RANS,并且对于耗散大的数值格式也能够给出令人满意的结果,是当前计算资源有限条件下的合理选择和切实可行的方法.因此自问世起就受到国内外湍流研究界的广泛关注,引发了RANS/LES混合方法的研究热潮[1,2].
SAS(Scale Adaptive Simulation)模型最早是由Menter等人于2003年提出[3],其核心思想是将冯卡门长度尺度(von Karman length scale)引入到RANS模型的尺度方程中.冯卡门长度尺度是由Rotta K-KL模型推导而来,具体形式为当地速度的一阶导数与二阶导数的比值.它能够依据当地流动结构动态地调整模型的长度尺度,从而使模型在稳定流动区域保持原有RANS模型的性能,而在不稳定流动区域允许大尺度非定常结构猝发到湍流能谱,具有类似LES的计算性能.相比于DES(Detached Eddy Simulation)方法,SAS模型由RANS到LES计算区域的过渡不依赖于网格尺度,不存在DES类方法的RANS/LES交界面问题,开辟了计算非定常湍流的新途径.目前Menter等人已将SAS模型推广到二方程SST,k-ε,k-ω模型中并广泛应用于工程问题的计算[4,5,6,7,8].
在此基础上,北京航空航天大学的徐晶磊、阎超等人将SAS模型推广到广泛应用于航空航天领域CFD计算的一方程SA模型中,构造了XY-SAS(Xu & Yan Scale Adaptive Simulation)模型[9].该模型提出了一个新型的、基于平均涡量与涡量梯度比值的三维冯卡门长度尺度.相比于Menter-SAS模型,XY-SAS模型构造的冯卡门长度尺度包含更丰富的流动信息、具有更直观的物理意义;同时,该模型的计算量要显著小于Menter等人构造的两方程SAS模型.但是,由于冯卡门长度尺度在湍流能谱的高波数区域无法提供足够的耗散,SAS类模型预测的湍流能谱存在高波数衰减不足的缺陷,需要进一步在湍流尺度中引入网格尺度作为限制器来提高SAS类模型的耗散.
本文采用不同形式的网格尺度限制器构造了3种XY-SAS模型,对Re=3 900的圆柱绕流展开数值模拟,分析不同形式的网格尺度限制器对模型计算性能的影响;并与DES方法及实验结果进行比较,评估XY-SAS模型对于大分离流动的模拟能力. 1 模型描述 1.1 SA模型
SA模型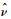
的输运方程[10]如下:
SA模型中涡黏性系数μt由下式给定:
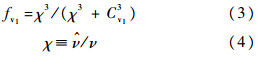
输运方程右端第1项是黏性的产生项,第2项是黏性的耗散项,最后两项为黏性的扩散项.耗散项中包含壁面距离d作为SA模型的湍流尺度. 1.2 冯卡门长度尺度
XY-SAS模型的三维冯卡门长度尺度定义为
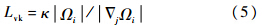
XY-SAS模型的核心思想是将冯卡门长度尺度引入到SA模型的湍流尺度——壁面距离d中,构造新的湍流尺度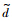
如下:
XY-SAS模型的优点在于不存在显式的RANS/LES转换开关,稳态的RANS和非稳态的LES区域过渡不依赖于网格形态,模型的湍流尺度能够根据当地流动结构自动调整.
但是,由于SAS类模型预测的湍流能谱存在高波数衰减不足的缺陷,需要进一步在湍流尺度中引入网格尺度Δ作为限制器,Cctr为调整限制器大小的控制参数.采用不同的网格尺度与控制参数可以构造出不同的限制器.
1.3.1 XY-SAS1
类比DES方法的网格尺度,以3个方向上的网格最大间距构造限制器,保证XY-SAS模型的涡黏性不小于DES方法的亚格子尺度涡黏性,与文献[11]中原始XY-SAS模型的构造方法一致.将Cctr设置为0.5,小于Spalart用各向同性衰减湍流标定的Smagorinsky常数(CDES=0.65),用以尽可能地激活冯卡门长度尺度,即SAS的计算.
仿照文献[3]中的早期SAS模型,以3个方向上的网格最小间距构造限制器,保证XY-SAS模型的冯卡门长度尺度不小于最小网格间距.与DES方法不同的是,此时网格尺度在XY-SAS模型中仅仅起到高波数衰减限制器的作用,对计算结果影响很小.Cctr经过各向同性衰减湍流标定为0.6.
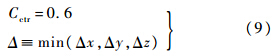
将Cctr设置为零,即不采用限制器,湍流尺度中完全不包含网格间距[12]. 2 结果与分析
圆柱绕流是典型的绕钝体流动,它既有不固定的分离点,又有分离后的尾流和脱体涡,具有丰富的流动现象,是湍流数值模拟中一个很有挑战性的经典算例.文献[13]分别对流动条件为Re=3 900的圆柱绕流做过模型实验,并且提供了尾涡在近壁面与远壁区不同站位处的时均速度场的实验结果.本文选择相同流动条件下的三维圆柱绕流展开数值模拟,来流Ma=0.2.
计算域在笛卡儿坐标系下表示,选取圆柱底部中心为坐标原点,x坐标轴方向与来流方向一致,y方向平行于圆柱横截面,沿圆柱展向取为z方向.根据Kravchenko和Moin[14]的数值实验研究,计算域中沿圆柱展向的长度取πD,此时流动可以充分发展,能较好地体现流动的三维性.圆柱绕流网格展向截面如图 1所示.计算网格在xy平面内采用O型网格,节点数为137×137,并在圆柱的边界层和尾迹区进行网格加密,保证第1层网格高度y+<1.壁面设置为无滑移的绝热壁,展向边界设为周期性边界条件.
 |
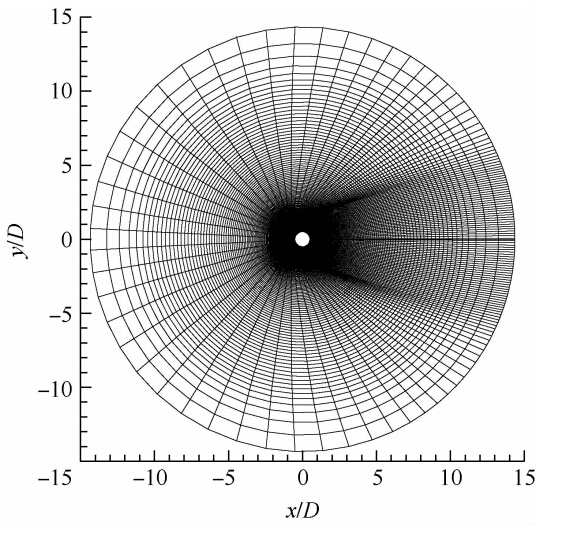| 图 1 圆柱绕流展向截面网格 Fig. 1 Two-dimensional grid of the z-slice domain |
图 2采用Q等值面显示了圆柱绕流的瞬时空间流场.从图 2可以看到,3种XY-SAS模型都得到了类似于DES的三维流场结构.绕流不仅在流向方向有旋涡的卷起和脱落,而且在展向方向也有大尺度的脉动.表明冯卡门长度尺度在大分离区允许大尺度非定常结构猝发到湍流能谱,具有类似LES的计算性能.
 |
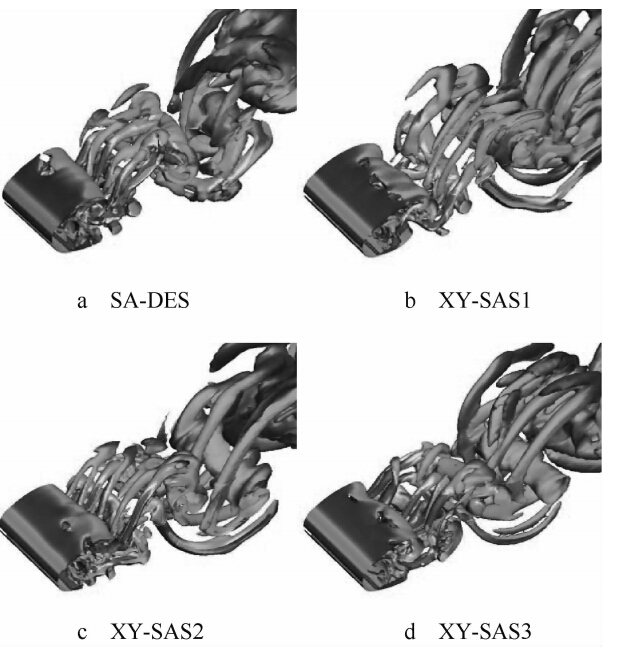| 图 2 瞬时流场结构图(Q=S2-Ω2=0.1/s2) Fig. 2 Instant turbulent structures(Q=S2-Ω2=0.1/s2) |
图 3比较了3种XY-SAS模型与DES的升力系数功率谱,通过升力系数自相关函数的Fourier变换得到,描述了信号功率随频率的分布特点.表 1列出了相应的阻力系数与表征圆柱尾流区涡脱落主频率的斯特劳哈尔数,并与文献[13,14,15]中的LES及实验结果相比较.由图 3、表 1可以看出,XY-SAS2的阻力系数及升力系数功率谱与DES,LES及实验结果最为接近;XY-SAS1计算的阻力系数较大,升力系数主频率偏高;XY-SAS3的阻力系数也略偏大,虽然准确预测了升力系数主频率,但在高频区功率谱明显偏高.
 |
| 图 3 升力系数功率谱密度分布 Fig. 3 Power spectral density (PSD) of the lifting coefficient |
| 计算模型 | CD | St |
| SA-DES | 1.046 | 0.208 |
| XY-SAS1 | 1.110 | 0.213 |
| XY-SAS2 | 1.039 | 0.208 |
| XY-SAS3 | 1.056 | 0.208 |
| LES | 1.04 | 0.208±0.01 |
| EXP | 0.98±0.05 | 0.208±0.02 |
图 4为圆柱壁面平均压力系数分布.图 5为尾迹中心线平均流向速度分布.从实验结果可以看出,流体绕过圆柱后,在圆柱尾部约D的范围内形成回流区,之后沿x正方向流速逐渐增大,最终达到较为平衡的状态,流速接近来流速度.其中XY-SAS2与DES及实验结果吻合较好.XY-SAS1计算得到的压力系数明显偏低,回流区长度最短,尾迹区中心线上的回流速度最小.虽然XY-SAS3预测的压力系数较为准确,但回流区长度也略小,回流速度偏低.
 |
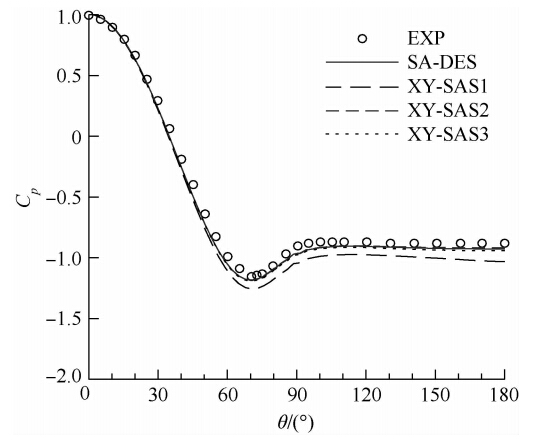| 图 4 壁面平均压力分布 Fig. 4 Pressure coefficients on the cylinder surface |
 |
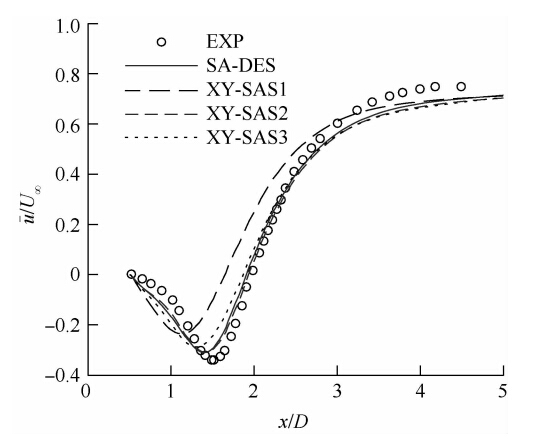| 图 5 尾迹区中心线流向平均速度分布 Fig. 5 Streamwise mean velocity on the centreline in the wake region |
图 6为近壁面尾迹区不同站位的流向与法向平均速度分布.图 7为不同站位的雷诺应力分布曲线.由图 6、图 7可以看出,XY-SAS2计算的平均速度分布与DES及实验结果吻合较好,雷诺应力与实验结果略有差异,但与DES结果相符合.当x/D=1.06时流向速度呈“U”型分布,相应的流向雷诺应力呈“M”型分布,且峰值较小.由此可见,采用最小网格间距可以为XY-SAS模型提供较好的高波数衰减限制,对于大分离流动能够达到DES的模拟能力,且不存在DES的RANS/LES交界面问题.
 |
| 图 6 近壁面尾迹区平均速度分布 Fig. 6 Mean velocity profile in the near wake region |
 |
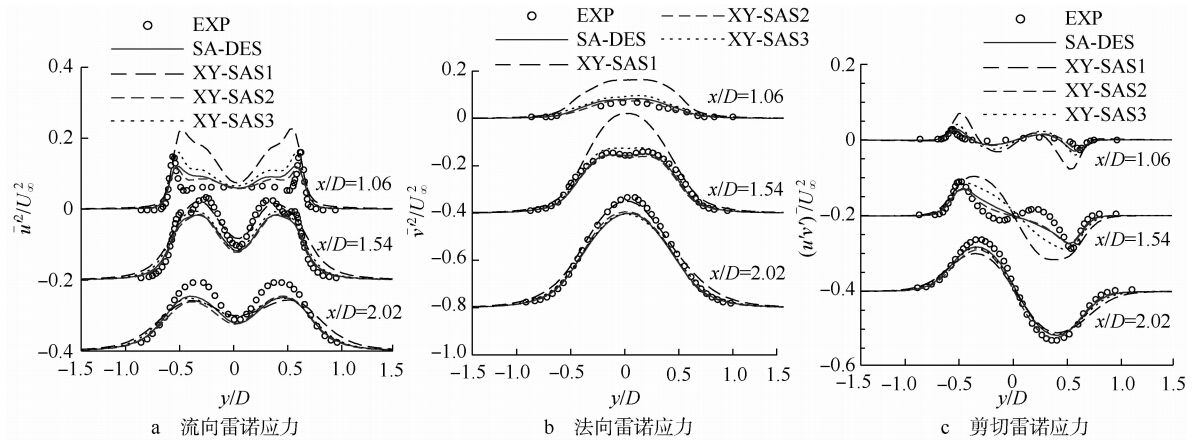| 图 7 近壁面尾迹区平均雷诺应力分布 Fig. 7 Mean Reynolds stress profile in the near wake region |
图 6中XY-SAS1计算得到的平均流向速度明显偏大,当x/D=1.06时近似“V”型分布,图 7中相应的流向雷诺应力峰值最大,法向及剪切雷诺应力与DES有明显差异.由此可见,文献[11]中原始XY-SAS采用的最大网格间距提供的限制过大,导致模型在高波数区域衰减太快,从而造成雷诺应力预测过大,对应的阻力系数偏大(表 1)、恢复压力系数不准确(图 4)、回流区长度变短(图 5).
XY-SAS3的计算结果总体与XY-SAS2相接近,但由于没有采用网格尺度限制器,XY-SAS3模型计算的雷诺应力略偏高,对应的阻力系数略偏大,回流区长度略短、回流速度偏低.因此,适当地引入网格尺度作为限制器可以改善模型在大分离区域的计算性能. 3 结 论
本文采用不同形式的网格尺度限制器构造了3种XY-SAS模型,对Re=3 900的圆柱绕流进行数值模拟,通过与DES方法及实验结果的比较,可以得出以下结论: ①采用网格尺度限制器可以改善XY-SAS模型在大分离流动区域的计算性能. ②采用最大网格间距提供的限制过大,导致模型在高波数区衰减太快,从而造成雷诺应力预测过大,回流区长度变短. ③采用最小网格间距可以提供较好的高波数衰减限制,对于大分离流动能够达到DES的模拟能力,且不存在DES的RANS/LES交界面问题,是较为合理的选择.
| [1] | Fröhlich J,von Teryi D.Hybrid LES/RANS methods for the simulation of turbulent flows[J].Progress in Aerospace Sciences,2008,44(5):349-377 |
| Click to display the text | |
| [2] | 阎超,于剑,徐晶磊,等.CFD模拟方法的发展成就与展望[J].力学进展,2011,41(5):562-589 Yan Chao,Yu Jian,Xu Jinglei,et al.On the achievements and prospects for the methods of computational fluid dynamics[J].Advance in Mechanics,2011,41(5):562-589(in Chinese) |
| Cited By in Cnki (46) | |
| [3] | Menter F R,Kuntz M,Bender R.A scale-adaptive simulation model for turbulent flow predictions[C]//41st Aerospace Sciences Meeting and Exhibit.Reston,VA:American Institute of Aeronautics and Astronautics Inc,2003-0767 |
| Click to display the text | |
| [4] | Menter F R,Egorov Y.A scale-adaptive simulation model using two-equation models[C]//43rd AIAA Aerospace Sciences Meeting and Exhibit.Reston,VA:American Institute of Aeronautics and Astronautics Inc,2005:271-283 |
| Click to display the text | |
| [5] | Menter F R,Egorov Y.The scale-adaptive simulation method for unsteady turbulent flow predictions.Part 1:theory and model description[J].Flow,Turbulence and Combustion,2010,85(1):113-138 |
| Click to display the text | |
| [6] | Egorov Y,Menter F R,Lechner R,et al.The scale-adaptive simulation method for unsteady turbulent flow predictions.Part 2:application to complex flows[J].Flow,Turbulence and Combustion,2010,85(1):139-165 |
| Click to display the text | |
| [7] | Menter F R,Schütze J,Kurbatskii K A,et al.Scale-resolving simulation techniques in industrial CFD[C]//6th AIAA Theoretical Fluid Mechanics Conference.Reston,VA:American Institute of Aeronautics and Astronautics Inc,2011-3474 |
| Click to display the text | |
| [8] | Menter F R.Review of the shear-stress transport turbulence model experience from an industrial perspective[J].International Journal of Computational Fluid Dynamics,2009,23(4):305-316 |
| Click to display the text | |
| [9] | 徐晶磊,阎超.一个一方程Scale-Adaptive Simulation模型的构造[C]//第14届全国计算流体力学会议.贵阳:[s.n.],2009:113-117 Xu Jinglei,Yan Chao.A one-equation scale-adaptive simulation model[C]//14th National Conference on CFD.Guiyang:[s.n. ],2009:113-117(in Chinese) |
| [10] | Spalart P R,Allmaras S R.A one-equation turbulence model for aerodynamic flows[C]//30th AIAA Aerospace Sciences Meeting and Exhibit.Reno,NV:American Institute of Aeronautics and Astronautics Inc,1992-0439 |
| Click to display the text | |
| [11] | 高瑞泽,徐晶磊,赵瑞,等.XY-SAS模型对分离流动的性能分析[J].北京航空航天大学学报,2010,36(4):414-418 Gao Ruize,Xu Jinglei,Zhao Rui,et al.Evaluation of XY-SAS model for separated flows[J].Journal of Beijing University of Aeronautics and Astronautics,2010,36(4):414-418(in Chinese) |
| Cited By in Cnki (1) | |
| [12] | Xu J L,Hu N,Gao G.A high-fidelity turbulence length scale for flow simulation[C]//Progress in Hybrid RANS-LES Modelling.Berlin:Springer,2012:141-145 |
| Click to display the text | |
| [13] | Ong L,Wallace J.The velocity field of the turbulent very near wake of a circular cylinder[J].Exp Fluids,1996,20(6):441-453 |
| Click to display the text | |
| [14] | Kravchenko A G,Moin P.Numerical studies of flow over a circular cylinder at ReD=3 900[J].Phys Fluids,2000,12(12):403-417 |
| Click to display the text | |
| [15] | Shim Y M,Sharma R N,Richards P J.Numerical study of the flow over a circular cylinder in the near wake at Reynolds number 3 900[C]//39th AIAA Fluid Dynamics Conference.Reston,VA:American Institute of Aeronautics and Astronautics Inc,2009-4160 |
