2. 中国航空工业集团公司 第一飞机设计研究院, 阎良 710000;
3. 西北工业大学 自动化学院, 西安 710129
2. The First Aircraft Institute, Aviation Industry Corporation of China, Yanliang 710000, China;
3. School of Automation, Northwestern Polytechnical University, Xi'an 710129, China
在实际工程中,系统可靠度优化是一项非常重要的研究内容,且多年来,对系统可靠度优化的研究已有大量文献[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13].为了设计一个具有高可靠度的系统,通常采用两种方式提高系统的可靠度:一是采用冗余形式,二是提高组件单元的可靠度.而提高组件单元的可靠度,不仅需要更精进的制造工艺,且需要更长的研制周期,从而使制造成本呈指数增加,但组件单元可靠度增加的非常有限.因此,在实际应用中,通常采用组件冗余的方式,提高整个系统的可靠度.
过去对系统可靠度的优化主要集中在假定构成组件的可靠度一定,在某种约束条件下,对系统的冗余进行分配.为了设计一个高可靠度的系统,Misra等人[4]提出了一个新的观点,即对组件的可靠度和冗余量同时进行优化分配.Garg等人[5]采用两阶段方法对系统可靠度-冗余度分配进行了研究,首先在第1阶段,基于蜂群免疫算法得到可靠度-冗余度优化分配的最优解,在此基础上,在冗余量固定的前提下得到组件可靠度的分配结果.高仁璟等人[6]采用遗传算法对电力系统的可靠度和余度进行了分配研究.文献[7]采用布谷鸟算法和遗传算法相结合的混合算法对4种类型的系统进行了可靠度-余度的分配与优化;Valian等人[8]提出基于惩罚引导的布谷鸟启发算法,用于系统可靠度-冗余度的优化和分配;为了更有效
地解决可靠度-冗余度的分配问题,Tan等人[9]提出了一种将粒子群(PSO)算法与差分进化(DE)和混沌局部搜索相结合的混合算法;而Wang等人[10]则将差分进化与协调搜索相结合解决可靠度-冗余度的连续优化和整数优化,使系统具有最优的可靠度.以上对可靠度-冗余度的分配研究均没有考虑具有表决结构的冗余度的分配对系统可靠度的影响.文献[13]对电路系统的交叉多表决器对冗余系统可靠度的影响进行了分析.
在前人研究的基础上,本文对飞行控制系统可靠度和冗余度的优化与分配进行了研究,并同时考虑了表决器对系统可靠度的影响.优化算法采用基于鱼群算法的混合算法,鱼群算法作为一种新型的群体智能优化方法,具有全局收敛性好,鲁棒性强等优点. 1 系统可靠度数学模型与分配算法
本文的研究对象为飞行控制系统,且假定该系统由4个子系统构成,即指令传感器组成的子系统、飞行控制计算机组成的子系统、作动器组成的子系统和速率陀螺组成的子系统.为了得到高可靠度的系统,各子系统均有冗余,且各冗余子系统均带有表决器.具有表决的冗余系统可靠度框图如图 1所示.
 |
| 图 1 具有表决的冗余系统可靠度框图Fig. 1 Reliability-redundancy diagram of voting system |
图 1中,mi表示第i子系统组件单元的冗余量,i=1,2,3,4.其中表决结构采用2/m表决进行系统可靠度的优化与分配.在进行系统可靠度的优化与分配前,先进行如下假设:
1) 各组件单元只有两种状态,即工作或失效;
2) 同一子系统的组件具有相同的可靠度;
3) 各组件单元以及各子系统相互独立;
4) 各表决器的结构和失效率具有一致性.
除作动器按照威布尔分布外,其余组件均按照指数分布. 1.1 可靠度数学模型
本文考虑在给定成本约束下,使系统的可靠度最大.具有表决的冗余系统可靠度模型如下.
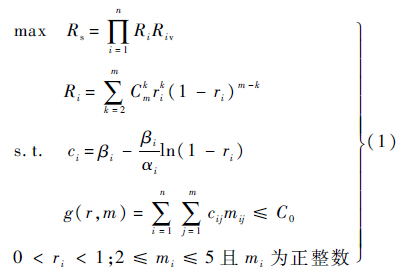
根据表达式(1)的形式,冗余数为3,4,5时的子系统可靠度和系统可靠度可以分别表示为
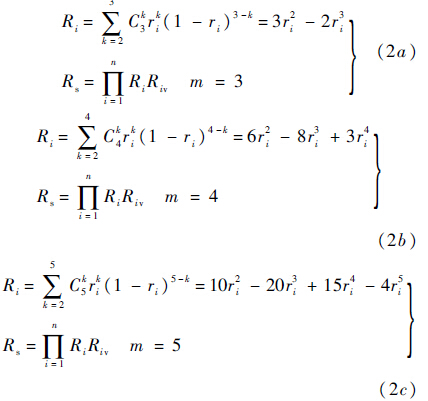
参照文献[14]中提出的方法,采用鱼群算法和增广拉格朗日乘子法相结合的混合算法进行系统可靠度的分配与优化. 1.2 分配算法
增广拉格朗日乘子法常用于约束函数的优化求解,而鱼群算法作为一种新型的群体智能优化方法,具有全局收敛性好、鲁棒性强等优点,且无需设定决策变量的初始值.
定义增广拉氏函数为
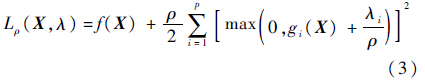

将约束优化问题转化成了无约束优化问题.
首先,定义惩罚参数初值为
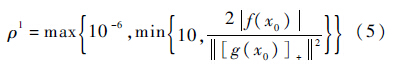
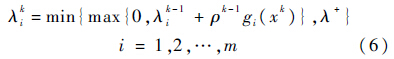
设定算法精度为ε*,迭代终止条件更新表达式为
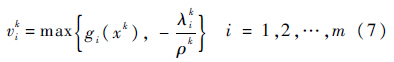
若满足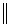 vik
vik ≤ε*或外部迭代达到最大迭代次数Kmax,则算法停止.否则,若
≤ε*或外部迭代达到最大迭代次数Kmax,则算法停止.否则,若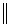 vk
vk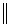 ≤α
≤α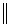 vk-1(
vk-1(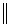 0<α<1),则停止惩罚;否则,按照一定的条件增大惩罚或减小惩罚.εk用于限制每次迭代过程中内部鱼群算法迭代的收敛精度.εk需满足k→∞时,εk→0.因此在本文中定义εk=max{ε*,10-k}.算法程序如图 2所示.
0<α<1),则停止惩罚;否则,按照一定的条件增大惩罚或减小惩罚.εk用于限制每次迭代过程中内部鱼群算法迭代的收敛精度.εk需满足k→∞时,εk→0.因此在本文中定义εk=max{ε*,10-k}.算法程序如图 2所示.
 |
| 图 2 分配算法流程Fig. 2 Allocation algorithm process |
程序的内部算法采用鱼群算法,用鱼群算法寻找增广拉氏函数的最优解,并将该最优解用于惩罚参数和拉氏参数等的更新.并需注意,将第k次得到的最优解作为第k+1次鱼群的一条人工鱼,其余人工鱼则随机生成.
鱼群算法的实现程序主要包括:初始化操作、觅食行为实现、聚群行为实现、追尾行为实现以及随机行为等.其中随机行为是觅食行为的一种缺省操作.影响算法的主要参数有:鱼群规模、迭代次数、视距、步长和拥挤度因子等.在本文中,视距参数采用自适应的方式实现,步长采用和决策变量有关的随机步长.
仿真说明本文采用的混合鱼群算法在处理约束优化问题中具有优良的全局收敛性能.选取文献[15]中的3个测试函数,仿真参数设定如下[9].鱼群算法的参数设定:鱼群规模Psize=160,最大迭代次数Gmax=100,g为迭代次数,拥挤度因子η=9,移动步长s=rand·max(Xmax-Xmin),遍历次数为10,视距v=δ·max(Xmax-Xmin).其中 仿真结果如表 1所示,并和文献[16]中的方法对比,说明本文所采用的优化方法能够较好地解决非线性函数的优化问题,优化得到的可行解具有较高的计算精度,且算法具有较好的稳定性,甚至对于较高维的优化函数也可以得到比较满意的可行解,如测试函数G02,维数为20.
仿真结果如表 1所示,并和文献[16]中的方法对比,说明本文所采用的优化方法能够较好地解决非线性函数的优化问题,优化得到的可行解具有较高的计算精度,且算法具有较好的稳定性,甚至对于较高维的优化函数也可以得到比较满意的可行解,如测试函数G02,维数为20.
以某型飞机的纵向俯仰运动控制系统为例,在成本约束下,采用本文提出的优化算法,对具有冗余和表决的系统进行可靠度的优化与分配.
系统参数设定如下:组件常数α=(1,3.5,2,5),β=(0.3,0.55,0.4,0.65).指令传感器的失效率λc=2.2×10-5,飞行控制计算机的失效率λfc=2.5×10-4,作动器失效率λa=1.449 2×10-3,速率陀螺失效率λr=5×10-4,且给定系统总成本为30. 2.1 冗余对系统可靠度的影响分析
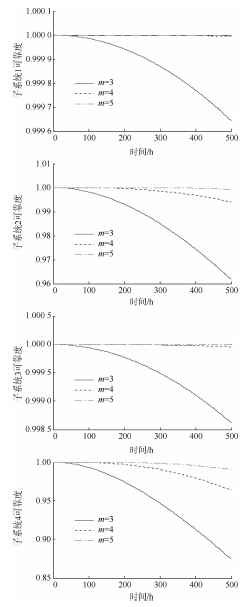
需要指出的是,表 2~表 5中的组件1,2,3,4分别代表组成子系统1,2,3,4的各组件单元.在对未优化系统进行可靠度分配时,本文采用[4, 4, 4, 5]的余度结构为例对比优化前与优化后的分配结果.同时不考虑表决器的失效,认为其完全可靠工作.系统未进行优化时分配的系统可靠度、各子系统可靠度以及各组件单元的可靠度如表 2所示,表 3说明未优化系统分配后的各组件的成本、子系统成本以及系统成本等,优化分配后的系统可靠度、各子系统可靠度以及各组件可靠度如表 4所示.优化后的系统成本、子系统成本和各组件成本如表 5所示.图 3和图 4分别说明了冗余对系统可靠度和子系统可靠度的影响.图 5表示了组件可靠度与成本间的函数关系.
| 组件可靠度 | 子系统可靠度 | 冗余 | 系统可靠度 | ||||||
| 组件1 | 组件2 | 组件3 | 组件4 | 子系统1 | 子系统2 | 子系统3 | 子系统4 | ||
| 0.827 870 35 | 0.517 855 84 | 0.924 564 65 | 0.966 996 62 | 0.982 233 71 | 0.713 794 43 | 0.998 380 09 | 0.999 994 22 | 4,4,4,5 | 0.699 973 17 |
| 0.839 367 58 | 0.878 870 07 | 0.871 566 23 | 0.696 113 51 | 0.985 418 3 | 0.993 536 75 | 0.992 342 1 | 0.967 726 3 | 4,4,4,5 | 0.940 196 25 |
| 0.827 738 95 | 0.585 593 34 | 0.853 023 04 | 0.515 916 42 | 0.982 195 01 | 0.803 807 55 | 0.988 699 85 | 0.831 762 51 | 4,4,4,5 | 0.649 252 48 |
| 0.847 414 31 | 0.658 549 74 | 0.975 111 02 | 0.517 223 04 | 0.987 415 97 | 0.881 542 09 | 0.999 939 48 | 0.833 287 65 | 4,4,4,5 | 0.725 290 28 |
| 0.827 549 | 0.581 305 87 | 0.559 498 84 | 0.749 182 03 | 0.982 138 97 | 0.798 598 97 | 0.771 054 43 | 0.984 182 45 | 4,4,4,5 | 0.595 199 2 |
| 组件可靠度 | 子系统可靠度 | 系统总成本 | 系统可靠度 | ||||||
| 组件1 | 组件2 | 组件3 | 组件4 | 子系统1 | 子系统2 | 子系统3 | 子系统4 | ||
| 0.827 852 19 | 0.664 376 2 | 0.916 895 86 | 1.093 448 9 | 3.313 408 77 | 2.658 550 48 | 3.667 583 46 | 5.467 244 52 | 15.104 787 2 | 0.699 973 17 |
| 0.848 590 98 | 0.881 711 52 | 0.810 468 39 | 0.804 843 13 | 3.394 363 94 | 3.526 846 07 | 3.241 873 56 | 4.024 215 67 | 14.187 299 2 | 0.940 196 25 |
| 0.827 623 26 | 0.688 428 33 | 0.783 495 89 | 0.744 314 70 | 3.310 493 03 | 2.753 713 30 | 3.133 983 57 | 3.721 573 51 | 12.919 763 4 | 0.649 252 48 |
| 0.864 008 68 | 0.718 858 37 | 1.138 666 06 | 0.744 666 07 | 3.456 034 74 | 2.875 433 48 | 4.554 664 26 | 3.723 330 33 | 14.609 492 8 | 0.725 290 28 |
| 0.827 292 65 | 0.686 810 87 | 0.563 968 44 | 0.829 793 61 | 3.309 170 58 | 2.747 243 48 | 2.255 873 76 | 4.148 968 07 | 12.461 255 9 | 0.595 199 2 |
| 组件可靠度 | 子系统可靠度 | 冗余 | 系统可靠度 | ||||||
| 组件1 | 组件2 | 组件3 | 组件4 | 子系统1 | 子系统2 | 子系统3 | 子系统4 | ||
| 0.993 563 65 | 0.993 563 65 | 0.989 348 52 | 0.991 963 44 | 0.999 999 06 | 0.999 999 99 | 0.999 999 94 | 0.999 999 98 | 5,5,5,5 | 0.999 998 971 |
| 0.993 449 59 | 0.992 592 15 | 0.985 354 14 | 0.981 125 91 | 0.999 999 99 | 0.999 998 38 | 0.999 999 77 | 0.999 999 38 | 5,4,5,5 | 0.999 997 522 |
| 0.972 748 35 | 0.989 807 77 | 0.999 681 12 | 0.987 508 11 | 0.999 997 30 | 0.999 999 95 | 0.999 999 999 9 | 0.999 999 88 | 5,5,5,5 | 0.999 997 13 |
| 0.986 005 09 | 0.980 471 15 | 0.975 740 703 | 0.997 153 12 | 0.999 999 81 | 0.999 999 28 | 0.999 998 302 | 0.999 999 999 6 | 5,5,5,5 | 0.999 997 396 |
| 0.995 826 63 | 0.999 420 99 | 0.998 936 37 | 0.993 428 72 | 0.999 999 71 | 0.999 999 999 | 0.999 999 995 | 0.999 999 991 | 4,4,4,5 | 0.999 999 695 |
| 组件可靠度 | 子系统可靠度 | 系统总成本 | 系统可靠度 | ||||||
| 组件1 | 组件2 | 组件3 | 组件4 | 子系统1 | 子系统2 | 子系统3 | 子系统4 | ||
| 1.460 582 2 | 1.342 910 46 | 1.308 411 28 | 1.277 088 07 | 7.302 911 01 | 6.714 552 3 | 6.542 056 38 | 6.385 440 36 | 26.944 960 1 | 0.999 998 971 |
| 1.808 468 3 | 1.320 819 49 | 1.244 719 48 | 1.166 095 51 | 9.042 341 7 | 5.283 277 97 | 6.223 597 38 | 4.945 748 56 | 26.379 694 6 | 0.999 997 522 |
| 1.380 792 4 | 1.270 677 55 | 2.010 140 25 | 1.219 747 78 | 6.903 962 01 | 6.353 387 75 | 10.050 701 26 | 6.098 738 91 | 29.406 789 9 | 0.999 997 13 |
| 1.580 718 48 | 1.168 492 65 | 1.1437 910 7 | 1.411 999 27 | 7.903 592 37 | 5.842 463 23 | 5.718 955 35 | 7.059 996 37 | 26.525 007 3 | 0.999 997 396 |
| 1.943 709 6 | 1.721 372 07 | 1.769 212 71 | 1.303 256 13 | 7.774 838 42 | 6.885 488 29 | 7.076 850 82 | 6.516 280 66 | 28.253 458 2 | 0.999 999 695 |
 |
| 图 3 冗余对系统可靠度的影响Fig. 3 Iimpact of redundancy on system reliability |
 |
| 图 4 冗余对子系统可靠度的影响Fig. 4 Impact of redundancy on subsystems reliability |
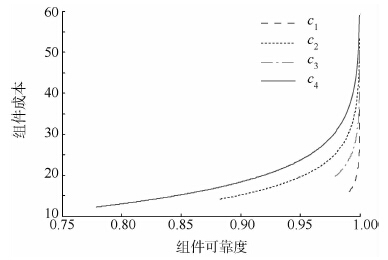 |
| 图 5 成本与组件可靠度的关系Fig. 5 Reliability relationship between costs and components |
首先,通过表 2~表 5中的数据对比,虽然未优化系统的成本降了下来,但系统可靠度最高仅达0.940 196 25;表 4的数据说明优化后系统的可靠度主要集中分布0.999 997~0.999 999,表 5中的系统总成本主要集中分布在26~29,数据分布比较均匀,说明文中采用的算法具有较强的全局收敛性,且算法的稳定性较好;其次,如果没有采用冗余结构,优化后的系统可靠度最高仅达到0.987 658,而采用冗余后的系统可靠度最高可以达到0.999 999 695,说明在现有制造工艺和成本限制下,冗余大大提高了系统的可靠度.得到的系统可靠度最优为0.999 999 695的优化结果中,系统冗余数为[4, 4, 4, 5],反而比其他几组数据的冗余度要少,这是因为组件可靠度比其他几的要高,这证明了提高系统可靠度的两种途径,即提高组件可靠度或采用冗余.综合表 4和表 5的结果,以组件1的可靠度和成本优化结果为例,在组件可靠度提高0.023 1时,成本就增加0.562 9,说明组件可靠度的提高要以花费高昂的成本为代价,图 5很好地证明这一点.
同时从图 3和图 4可以清楚地看到,冗余度的不同对系统可靠度和子系统可靠度的显著影响,同时发现冗余度为4和5的系统可靠度曲线几乎完全重合,说明系统可靠度的提高并不是采用冗余越多越好.另外,在系统可靠度不小于0.99的要求下,冗余度为3的系统能够维持时间约为107 h,而冗余度为4和5的系统可以持续到288 h.因此,在可用资源有限的条件下,目前飞行控制系统大多选用4余度配置结构. 2.2 表决器对系统可靠度的影响分析
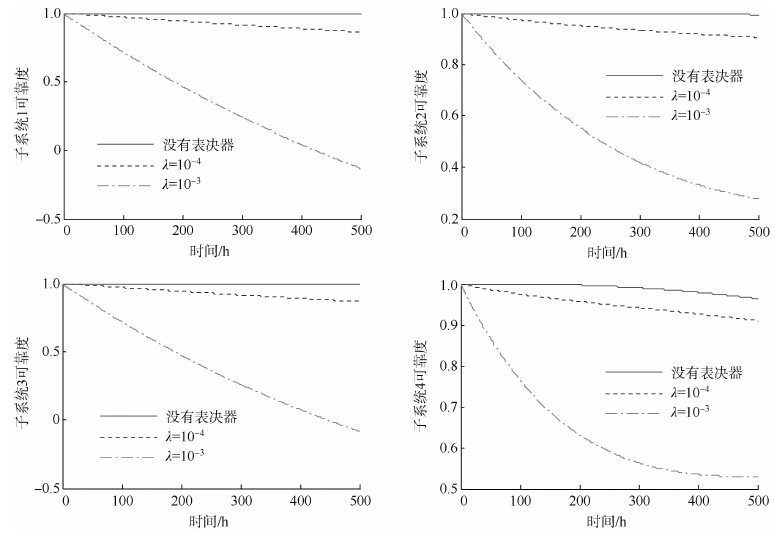
以4余度配置系统为例,时间设定为500 h,分析表决器失效率对系统可靠度和子系统可靠度的影响.图 6中表决器的失效率设定为: λv1=10-7,λv2=10-5,λv3=10-4,λv4=10-3.图 7中以λv=10-4为例,分析说明表决器的失效率对子系统可靠度影响.
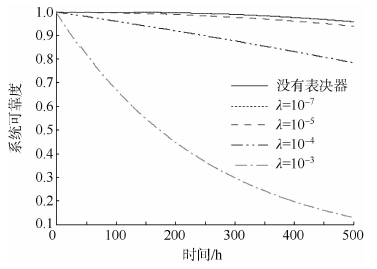 |
| 图 6 表决器对系统可靠度的影响Fig. 6 Impact of voters on system reliability |
 |
| 图 7 表决器对子系统可靠度的影响Fig. 7 Impact of voters on subsystems reliability |
从图 6中,可以清楚地看到,在表决器失效率λv≤10-7的条件下,系统可靠度曲线几乎和不考虑表决器失效时完全重合.当不考虑组成系统单元组件失效时,随着表决器失效率的增大,系统可靠度急剧下降,当表决器失效率λv≥10-3时,系统能够保持在可靠度不小于0.99的时间不足2.5 h,这是因为随着表决器失效率的增大,子系统的可靠度急剧下降,图 6清晰地说明了这种变化.
综合图 6和图 7的表决器对系统可靠度和子系统可靠度的影响变化曲线,发现,即使组件单元工作完好,一旦表决器出现故障,则系统将出现故障.因此,为了使系统能够在比较长的时间内保持较高的任务可靠度,除了使用组件单元冗余配置结构外,还应设法提高表决器的可靠度. 3 结 论
通过测试函数的仿真分析,说明了本文提出的鱼群算法和增广拉格朗日乘子法相结合的混合优化算法能够有效地处理函数极值问题的优化求解,同时将该混合算法用于飞行控制系统可靠度和冗余度的同时优化与分配,通过仿真分析可以得出:
1) 分配结果进一步证明了该算法具有较强的全局收敛性和较好的算法稳定性;
2) 证明了采用余度配置可以大大提高系统的可靠度,改善系统的可靠性;
3) 仿真分析了表决器的失效率对系统可靠度的影响,说明改善系统的可靠度不仅要恰当地配置系统冗余,同时也要注意改善表决器的可靠度.因此,目前在实际工程中,除了采用组件系统冗余,同时也注重表决器结构的冗余配制,保证系统更可靠地工作.
| [1] | Fyffe D E,Hines W W,Lee N K.System reliability allocation and a computational algorithm[J].Reliability,IEEE Transactions on,1968,17(2):64-69 |
| Click to display the text | |
| [2] | Ravi V,Reddy P J,Zimmermann H J.Fuzzy global optimization of complex system reliability[J].Fuzzy Systems,IEEE Transactions on,2000,8(3):241-248 |
| Click to display the text | |
| [3] | Lim M H,Teoh A B J,Toh K A.An efficient dynamic reliability-dependent bit allocation for biometric discretization[J].Pattern Recognition,2012,45(5):1960-1971 |
| Click to display the text | |
| [4] | Misra K B,Ljubojevic M D.Optimal reliability design of a system:a new look[J].Reliability,IEEE Transactions on,1973,22(5):255-258 |
| Click to display the text | |
| [5] | Garg H,Rani M,Sharma S P.An efficient two phase approach for solving reliability-redundancy allocation problem using artificial bee colony technique[J].Computers & Operations Research,2013,40(12):2961-2969 |
| Click to display the text | |
| [6] | 高仁璟,刘书田.基于遗传算法的复杂系统可靠度和冗余数设计分配优化[J].大连理工大学学报,2002,42(6):741-744 Gao Renjing,Liu Shutian.Reliability and redundancy optimal planning for complex system using genetic algorithm[J].Journal of Dalian University of Technology,2002,42(6):741-744(in Chinese) |
| Cited By in Cnki (4) | |
| [7] | Kanagaraj G,Ponnambalam S G,Jawahar N.A hybrid cuckoo search and genetic algorithm for reliability-redundancy allocation problems[J].Computers & Industrial Engineering,2013,66(4):1115-1124 |
| Click to display the text | |
| [8] | Valian E,Valian E.A cuckoo search algorithm by Lévy flights for solving reliability redundancy allocation problems[J].Engineering Optimization,2013,45(11):1273-1286 |
| Click to display the text | |
| [9] | Tan Y,Tan G,Deng S.Hybrid particle swarm optimization with differential evolution and chaotic local search to solve reliability-redundancy allocation problems[J].Journal of Central South University,2013,20(6):1572-1581 |
| Click to display the text | |
| [10] | Wang L,Li L.A coevolutionary differential evolution with harmony search for reliability-redundancy optimization[J].Expert Systems with Applications,2012,39(5):5271-5278 |
| Click to display the text | |
| [11] | Sheikhalishahi M,Ebrahimipour V,Shiri H,et al.A hybrid GA-PSO approach for reliability optimization in redundancy allocation problem[J].The International Journal of Advanced Manufacturing Technology,2013,68(1-4):317-338 |
| Click to display the text | |
| [12] | Mahato S K,Sahoo L,Bhunia A K.Reliability-redundancy optimization problem with interval valued reliabilities of components via genetic algorithm[J].J Inf Comput Sci,2012,7(4):284-295 |
| [13] | 伊小素,邓燕,潘雄,等.表决器对分层三模冗余系统可靠性影响分析[J].中国惯性技术学报,2011,19(4):494-498 Yi Xiaosu,Deng Yan,Pan Xiong,et al.Voter's influence on reliability of partitioned triple modular redundancy system[J].Journal of Chinese Inertial Technology,2011,19(4):494-498(in Chinese) |
| Cited By in Cnki (5) | |
| [14] | Rocha A M A C,Martins T F M C,Fernandes E M G P.An augmented Lagrangian fish swarm based method for global optimization[J].Journal of Computational and Applied Mathematics,2011,235(16):4611-4620 |
| Click to display the text | |
| [15] | Thomas P R,Yao X.Stochastic ranking for constrained evolutionary optimization[J].IEEE Transactions on Evolutionary Computation,2000,4(3):284-294 |
| Click to display the text | |
| [16] | Barbosa H J C,Lemonge A C C.An adaptive penalty method for genetic algorithms in constrained optimization problems[M].Vienna:In Tech Education and Publishing,Vienna Austria,2008:9-34 |


