表1(Table 1)
航行体在水下高速运动时,其表面附近的水因为低压而发生空化现象.当航行体速度很高时,空泡会完全包裹航行体,形成超空泡[1].超空泡的形成使得航行体在水下运动的阻力明显减小,从而可大幅度提高航行体的水下航行速度[2].
当超空泡射弹在水中运动时,任何微小的扰动,
如射弹在发射出膛或不稳定流动引起的微小扰动等都可能使射弹尾部与空泡壁面发生连续撞击,称之为尾拍现象[3].近年来,高速超空泡射弹的尾拍运动引起了国内外学者的广泛关注和研究,主要集中于研究其流体动力学特性等[4].Ruzzene等人[5, 6]建立了尾拍运动的撞击力学模型,分析了尾拍力作用下航行体的结构响应.Savchenko等人利用开放式水洞测试了圆柱形航行体在空泡内部滑行时的尾部流体动力[7, 8, 9, 10, 11].国内方面,曹伟等人[12]通过高速射弹试验对超空泡的形态特性和发展规律进行了深入研究.金大桥等人[13]设计了一种通气超空泡水下射弹试验,对射弹的空泡形态进行了试验研究.何乾坤等人[14]对超空泡射弹尾拍运动结构动力学响应和空泡摆动对超空泡射弹尾拍运动的影响进行了分析.对于不同用途和性能的超空泡射弹,其局部构造具有一定的差异,相应地，射弹质心位置也不同,表现为射弹的转动惯量有所差异,导致射弹发生尾拍运动时的转动周期不同,进而影响射弹的流体动力学和结构动力学性能,可能会因共振或强度、抗弯刚度不足而导致结构失效,因此研究不同质心位置对超空泡射弹结构运动参数和空泡形态的影响具有重要的实际工程意义.
本文对超空泡射弹尾拍运动引起的射弹转动、空泡形态变化等开展了数值模拟研究,对比分析了质心位置对射弹尾拍运动弹体转动、空泡形态、尾拍阻力和升力等的影响,从而加深对超空泡射弹运动过程中尾拍现象的认识,同时为超空泡射弹结构设计提供参考.
1 数值计算方法 1.1 控制方程
连续性方程:
动量方程:
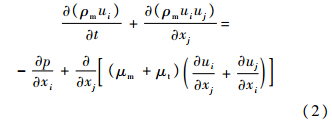
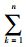αkρk为混合物的密度;μm=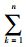αkμk为混合物的动力黏性系数.1.2 湍流模型
湍流是流场结构中的一种强非线性流体状态,是空化流场的主要特征之一.在空泡的发展尤其是尾部闭合阶段均存在着湍流现象.文中所采用的湍流模型为SST(Shear Stress Transport).基于Baseline k-ω的SST湍流模型通过计算湍流剪切应力的输运方式,对于逆压梯度下的流动分离问题有了更为精准的预测.Baseline k-ω湍流模型的控制方程如下[15]:
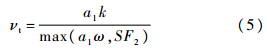
1.3 空化模型
对于多相流场的空化问题而言,空化数是描述流场空化强弱的特征参数,表示为
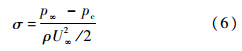
当流场中发生空化现象时的水蒸汽和水两相之间的质量转换输运方程为
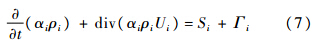
空化模型采用基于Rayleigh-Plesset方程的简化形式:
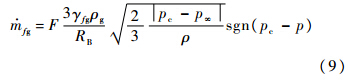
1.4 刚体运动方程与网格变形方法
超空泡射弹尾拍运动的影响因素较多,使得研究尾拍运动比较复杂,国内外对超空泡射弹尾拍运动的研究往往假设射弹的轴线为一直线,在计算过程中也采用此假设.计算时将射弹头部切除一层网格的厚度以与主体分离,固定射弹头部,转动中心于头部截面中心位置,这样做可以消除头部攻角引起的空泡形态变化对尾拍流场研究的影响.同时将射弹主体简化为刚体,引入刚体运动方程实现射弹在流场力作用下的运动规律求解.射弹运动方程定义如下:
超空泡射弹尾拍运动的研究涉及动网格的计算问题,本文使用位移扩散模型(displacement diffusion model)计算尾拍运动中的动网格问题.具体定义如下:
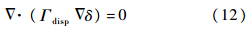
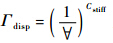为网格刚度,衡量网格变形的能力,文中取值为10，∀为网格体积.2 计算模型与方法验证 2.1 计算模型与网格
本文计算采用的射弹模型为具有大长细比的圆柱体,头部空化器为圆盘形,空化器直径与弹体直径相同,均为8mm,弹体长度为160mm,弹体长细比为20.射弹模型如图 1所示.
 |
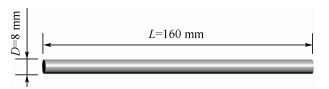| 图 1 射弹模型 Fig. 1 Model of projectile |
射弹尺寸及属性如表 1所示.
| 参数 | L/mm | D/mm | 密度ρs/(kg/m3) | 转动惯量Iz/(kg·m2) |
| 数值 | 160 | 8 | 7820 | 5.369×10-4 |
计算流域及边界条件设置如图 2所示,坐标原点位于射弹头部中心处,x轴与射弹轴线重合,在入口处采用速度入口的边界条件,在侧壁和出口均采用压力出口的边界条件,计算域的参考压力为101325Pa,高速运动时重力对空泡形态的影响较小,文中计算忽略重力作用.
 |
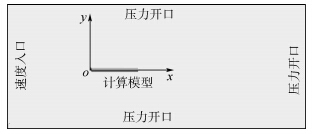| 图 2 计算域及边界条件设置 Fig. 2 Computational domain and boundary conditions |
计算域网格划分如图 3所示.本文采用的计算网格均为六面体结构化网格,在射弹头部和空泡闭合区域附近等压力梯度变化较大的流场区域对网格进行加密处理,考虑到需要对尾拍运动撞击空泡壁面时的精确捕捉,对射弹尾部也进行了加密处理,边界层网格厚度为0.2mm.
 |
| 图 3 计算域网格划分 Fig. 3 Mesh of computational domain |
针对图 1所示的射弹模型,建立了精细(50万)、中等精细(35万)、粗糙(13万)3种不同精度的网格,对3种精度网格的计算结果进行了对比分析.
不同网格精度下射弹超空泡尾部闭合区域的压力系数变化如图 4所示.射弹头部的压力系数变化如图 5所示.从图中可以看出,对于头部附近区域的压力系数变化,不同网格数量的计算结果差异较小,而对于空泡闭合区域3种网格的计算结果有所差别,其中精细网格(50万)和中等精细网格(35万)的计算结果几无差异,而粗糙网格(13万)的计算结果与精细网格和中等精细网格的计算结果有着明显差异,因此为了节省计算资源,并且达到计算所需求的精度,下文选用中等精细网格(35万)进行计算.
 |
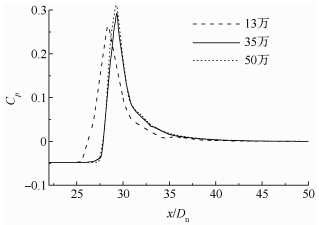| 图 4 不同网格精度下空泡闭合区域压力系数对比 Fig. 4 Comparison of pressure coefficient of cavity closure area with different mesh density |
 |
| 图 5 不同网格数量下射弹头部附近压力系数对比 Fig. 5 Comparison of pressure coefficient of projectile head area with different mesh density |
首先使用不同的湍流模型(k-ε湍流模型、k-ω湍流模型、SST湍流模型)对射弹的空化流场进行计算得到流场压力及空泡轮廓,如图 6所示.从图中可以看出,3种模型的头部流场压力差别不大,主要差别在于空泡的长度和射弹尾部回射流的强弱.SST湍流模型的空泡长度和回射流的强弱介于其他二者之间.为验证计算结果的有效性,将3种湍流模型计算的空泡外形与Lognovinch独立膨胀原理[16]所得的空泡外形对比,如图 7所示. 由图 7可以看出,数值计算与独立膨胀原理所得的空泡外形在空泡前体几乎一致,但在空泡闭合区域附近有一定的差异,SST湍流模型的空泡外形与独立膨胀原理计算所得的空泡外形差别较小.超空泡尾部闭合区域的压力系数分布如图 8所示.SST湍流模型的计算结果也介于其他两种模型之间.综合以上因素,本文选用SST湍流模型进行计算.
 |
| 图 6 不同湍流模型计算的射弹空化流场 Fig. 6 Comparison of the projectile cavitation flow field using different turbulence models |
 |
| 图 7 不同湍流模型及独立膨胀原理所得空泡轮廓比较 Fig. 7 Comparison of cavity profiles using different turbulence models and principle of independence cavity section expansion |
 |
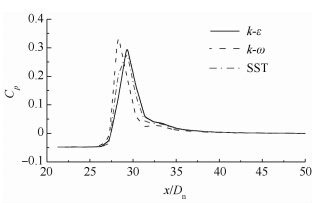| 图 8 不同湍流模型空泡闭合区域压力系数分布 Fig. 8 Comparison of pressure coefficient of cavity closure area using different turbulence models |
本文针对4种不同质心位置(如图 9所示)的超空泡射弹尾拍运动问题开展了相关研究,I1~I4为不同质心位置下弹体相对于头部转轴的转动惯量(如表 2所示),I2为质心位于几何中心时的转动惯量.空化数为0.048,初始扰动角速度假设为θ·0=8rad/s.
 |
| 图 9 射弹不同质心位置示意图 Fig. 9 Schematic of different mass centers of projectile |
| 参数 | I1 | I2 | I3 | I4 |
| 数值 | 4.846 | 5.369 | 5.637 | 6.215 |
以空化数σ=0.048,绕弹体头部转轴的转动惯量I2=5.369×10－4kg·m2,θ·0=8rad/s的射弹运动为例来分析射弹尾拍运动在一个周期T的空泡形态变化,如图 10所示.
 |
| 图 10 射弹尾拍运动空泡形态变化 Fig. 10 Change of cavity shape due to tailslap of projectile |
由图 10可以看出,射弹的尾拍运动将引起空泡形态变化,破坏空泡原有的对称壁面.在弹体尾部与空泡壁面碰撞的位置,空泡形态发生显著的改变,弹体与空泡壁面碰撞位置之后的空泡形态发生改变.弹体与空泡壁面的碰撞增大了尾部空泡的截面面积,同时也破坏了空泡的对称性.发生碰撞期间,射弹尾部的空泡朝着弹体运动的方向发展.
3.2 质心位置对射弹刚体运动的影响分析
图 11~图 14分别给出了不同质心位置的射弹在尾拍运动过程中的转角、转动角速度、角加速度以及尾拍周期随时间的变化规律.
图 11~图 13表明,不同质心位置下的超空泡射弹尾拍运动的转角、转动角速度和角加速度都呈现出周期性的变化.这种周期性变化是由初始扰动引起的射弹在空泡内的转动与空泡壁面的碰撞所产生.该碰撞过程涉及汽、液、固等多相之间的能量传递和转换,存在能量耗散,因此会引起射弹转动角速度、角加速度等的迅速衰减.不同质心位置下射弹转角、转动角速度以及角加速度的时间历程曲线表明,射弹的转动惯量越大,即质心离射弹头部越远,射弹刚体运动的参量变化越滞后,体现为射弹的转角、角速度、角加速度的周期越长.图 14表明了尾拍周期随着尾拍次数的增加而变大,且质心与头部距离越大,周期也越大.
 |
| 图 11 不同质心位置下的射弹转角变化 Fig. 11 Change of projectile rotation angle of different mass centers |
 |
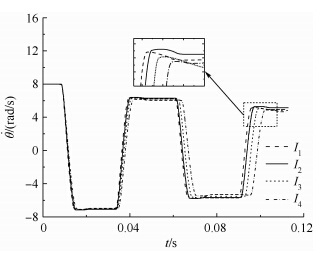| 图 12 不同质心位置下的射弹转动角速度变化 Fig. 12 Change of projectile angular velocity of different mass centers |
 |
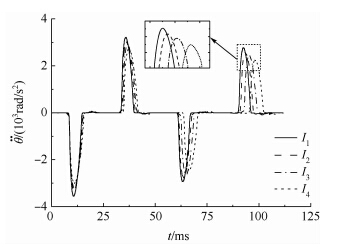| 图 13 不同质心位置下的射弹转动角加速度变化 Fig. 13 Change of projectile angular acceleration of different mass centers |
 |
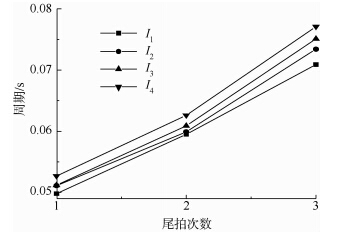| 图 14 射弹尾拍周期随尾拍次数的变化 Fig. 14 Change of projectile tailslap cycle with tail-slaps numbers |
通过开展超空泡射弹以在同一空化数(σ=0.048)不同质心位置下的三维数值计算,得到了超空泡射弹尾拍运动中的射弹尾拍阻力(射弹撞击空泡壁面的撞击力在射弹前进速度方向上的分力)的变化如图 15所示,射弹尾拍升力(射弹撞击空泡壁面的撞击力在垂直于射弹前进速度方向上的分力)如图 16所示.
 |
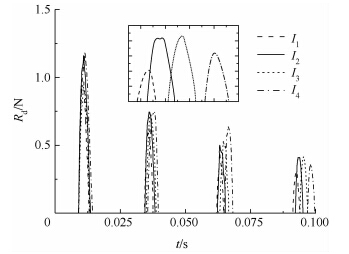| 图 15 不同质心下射弹尾拍阻力的变化 Fig. 15 ChangeChange of projectile tailslap resistance force of different mass centers |
 |
| 图 16 不同质心下射弹尾拍升力的变化 Fig. 16 Change of projectile tailslap lift force of different mass centers |
图 15和图 16表明,射弹在空泡内的转动,使得射弹与空泡壁面的撞击力呈现出明显的周期性变化,具体体现在射弹尾拍阻力和尾拍升力的周期性变化.同时,随着射弹质心距头部越远,转动惯量越大,射弹尾拍运动的周期越大.从图 15和图 16中可以看出,射弹转动惯量越大,尾拍阻力和尾拍升力的变化周期也越大.
4 结 论
本文通过求解混合介质的RANS方程、SST湍流方程和不同介质之间的质量输运方程,研究了超空泡射弹尾拍运动的空泡形态变化,对比分析了不同质心位置下的刚体运动参量和尾拍力的变化,得到如下结论：
1) 超空泡射弹的尾拍运动将破坏空泡形态的对称性,弹体与空泡壁面发生碰撞的位置,空泡壁面朝着弹体转动的方向发展.
2) 超空泡射弹尾拍运动的转动角度、角速度和角加速度都表现出周期性.当射弹的质心位置越靠后,射弹的转动惯量越大时,射弹尾拍运动的转动角度、角速度和角加速度的周期越大.
3) 超空泡射弹尾拍运动时的尾拍阻力和尾拍升力都呈现出周期性,且射弹的质心越靠后,转动惯量越大,尾拍阻力和尾拍升力的变化周期也越大.
| [1] | 孟庆昌,张志宏,刘巨斌,等.水下高速航行体超空泡流动研究进展[J].船海工程,2006(6):26-29 Meng Qingchang,Zhang Zhihong,Liu Jubin,et al.Research development of high-speed underwater vehicle[J].Journal of Marine Science and Application,2006(6):26-29(in Chinese) |
| Cited By in Cnki (12) | |
| [2] | Savchenko Y N.Control of supercavitation flow and stability of supercavitating motion of bodies[C]//VKI Special Course on Supercavitating Flows.Brussels:RTO2AVT and VKI,2001:313-341 |
| [3] | 孟庆昌,张志宏,顾建农,等.超空泡射弹尾拍分析与计算[J].爆炸与冲击,2009,29(1):56-60 Meng Qingchang,Zhang Zhihong,Gu Jiannong,et al.Analysis and calculation for tail-slaps of supercavitating projectiles[J].Explosion and Shock Waves,2009,29(1):56-60(in Chinese) |
| Cited By in Cnki (23) | |
| [4] | Kulkarni S S,Pratap R.Studies on the dynamics of a supercavitating projectile[J].Applied Mathematical Modeling,2000,24(2):113-129 |
| Click to display the text | |
| [5] | Ruzzene M,Soranna F.Impact dynamics of elastic stiffened supercavitating underwater vehicles[J].Journal of Vibration and Control,2004,10(2):243-267 |
| Click to display the text | |
| [6] | Ruzzene M,Kamada R,Bottasso C L,et al.Trajectory optimization strategies for supercavitating underwater vehicles[J].Journal of Vibration and Control,2008,14(5):611-644 |
| Click to display the text | |
| [7] | Savchenko Y N.Experimental investigation of supercavitating motion of bodies[C]//Van den Braembussche R.RTO AVT Lecture Series on“Supercavitating Flows”.Brussels:VKI,2001(4):1-24 |
| [8] | Vasin A D.Immersion of a cylinder in a fluid through a cylindrical free surface[J].Fluid Dynamics,2001,36(2):169-177 |
| Click to display the text | |
| [9] | Kubenko V D.Impact of a long thin body on a cylindrical cavity in liquid:a plane problem[J].International Applied Mechanics,2006,42(6):32-53 |
| [10] | Kubenko V D,Gavrilenko O V.Impact of a spherical rigid body on the surface of a cavity in a compressible liquid an axisymmetric problem[J].International Applied Mechanics,2008,44(1):8-15 |
| Click to display the text | |
| [11] | Kubenko V D,Gavrilenko O V.Impact interaction of cylindrical body with a surface of cavity during supercavitation motion in compressible fluid[J].Journal of Fluids and Structures,2009,25(5):794-814 |
| Click to display the text | |
| [12] | 曹伟,王聪,魏英杰,等.自然超空泡形态特性的射弹试验研究[J].工程力学,2006,23(12):175-187 Cao Wei,Wang Cong,Wei Yingjie,et al.High-speed projectile experimental investigations on the characteristics of natural supercavitation[J].Engineering Mechanics,2006,23(12):175-187(in Chinese) |
| Cited By in Cnki (72) | |
| [13] | 金大桥,王聪,魏英杰,等.通气超空泡水下射弹实验研究[J].工程力学,2011,28(9):214-222 Jin Daqiao,Wang Cong,Wei Yingjie,et al.Experimental study of ventilated supercavity by underwater projectile[J].Engineering Mechanics,2011,28(9):214-222(in Chinese) |
| Cited By in Cnki (7) | |
| [14] | 何乾坤,魏英杰,尤天庆,等.空泡摆动对超空泡航行体尾拍影响分析[J].北京航空航天大学学报,2012,38(4):509-512 He Qiankun,Wei Yingjie,You Tianqing,et al.Analysis of tail-slaps of supercavitating vehicle influenced by distortion of cavity shape[J].Journal of Beijing University of Aeronautics and Astronautics,2012,38(4):509-512(in Chinese) |
| Cited By in Cnki (12) | |
| [15] | Menter F R.Two-equation eddy-viscosity turbulence models for engineering applications[J].AIAA-Journal,1994,32(8):1598-1605 |
| Click to display the text | |
| [16] | Savchenko Y N,Semenenko V N,Serebryakov V V.Experimental study of the supercavitation flows at subsonic flow velocities[J].Doklady AN Ukrainy,1992,2(2):64-69 |
