SDUV方法中组织振动信号提取算法比较

Download PDF 打印本文

文章快速检索

高级检索

引用本文

蔡夕然, 樊璠, 李晓斐, 牛海军. SDUV方法中组织振动信号提取算法比较[J]. 北京航空航天大学学报, 2014, 40(12): 1761-1766 复制到剪切板

Cai Xiran, Fan Fan, Li Xiaofei, Niu Haijun. Comparison of tissue vibration signal extraction algorithms in shearwave dispersion ultrasound vibrometry[J]. Journal of Beijing University of Aeronautics and Astronsutics, 2014, 40(12): 1761-1766. 复制到剪切板

SDUV方法中组织振动信号提取算法比较

蔡夕然, 樊璠, 李晓斐, 牛海军

北京航空航天大学生物与医学工程学院, 北京 100191

收稿日期:2014-01-08; 网络出版日期: 2014-04-11

基金项目：国家自然科学基金资助项目(31170896).

作者简介: 蔡夕然(1989-),男,江西鹰潭人,硕士生,colepfieffer08@gmail.com

通讯作者：牛海军,hjniu@buaa.edu.cn

摘要：组织振动信号的提取是剪切波频散超声振动成像技术(SDUV)方法中的重要步骤.目前,SDUV方法中有两种常用的组织振动信号提取算法,正交解调法(QDM)和互功率谱法(CSM),但是未见比较这两种算法提取质量差异的相关研究.因此,构造了不同信噪比(SNR_U)的参数化仿真超声回波信号模型,分别使用QDM和CSM从超声回波信号中提取组织振动信号,比较了两种方法的提取效果与计算效率.实验结果表明,当SNR_U≥35 dB,两种算法在相同信噪比下提取出的信号所分离出的振动相位结果相近,标准差均小于1°,对于剪切波波速的计算结果没有太大影响.CSM的计算效率低于QDM的计算效率.因此,当SNR_U<35 dB,为了减小振动信号初始相位的提取误差,应该使用CSM提取组织的振动信号.当SNR_U≥35 dB,应该选择QDM提取组织的振动信号,以减少信号处理时间.本研究的发现有助于提高SDUV方法的检测效率.

关键词： SDUV 信噪比振动信号提取正交解调法互功率谱法

Comparison of tissue vibration signal extraction algorithms in shearwave dispersion ultrasound vibrometry

Cai Xiran, Fan Fan, Li Xiaofei, Niu Haijun

School of Biological Science and Medical Engineering, Beijing University of Aeronautics and Astronautics, Beijing 100191, China

Abstract:Vibration extraction is an important step in shearwave dispersion ultrasound vibrometry (SDUV). There are two primary algorithms for vibration extraction in SDUV, the quadrature demodulation method (QDM) and the cross-spectrum method (CSM). However, the extraction qualities of QDM and CSM are under appropriate comparison. This study aimed at comparing the performance of QDM and CSM for tissue vibration extraction based on a parameterized model under various signal-to-noise ratio of ultrasound echoes (SNR_U). Results show that when SNR_U≥35 dB, the standard deviations of the estimated vibration phase using the vibration extracted by the two methods are close, which has no significant influence on the calculation result of the shear wave speed. The computation efficiency of CSM for vibration extraction is lower than that of QDM. As a conclusion, when SNR_U<35 dB, the tissue vibration should be extracted by CSM to suppress the error of vibration phase estimation. However, when SNR_U≥35 dB, the tissue vibration should be extracted by QDM to reduce the signal processing time. The findings may provide some strategy in SDUV, which can optimize the examination protocol and make it more efficient.

Key words: SDUV signal-to-noise ratio (SNR) vibration extraction quadrature demodulation method (QDM) cross-spectrum method (CSM)

一般来说,当组织发生病变时,组织的黏弹性等力学特性的变化往往早于组织形态的改变,因此,有效提取组织的力学特征对于疾病的早期诊断具有重要的临床价值^{[1, 2]}.1991年Ophir等提出了超声弹性成像(ultrasound elastography)的概念与技术,该技术主要运用超声测量受压组织不同位置的位移,通过超声回波估计组织形变状况,进一步计算组织相对弹性模量,并应用组织不同位置的相对弹性模量来成像,进行疾病的早期诊断^[3].

近年来,超声弹性成像技术得到了迅速的发展,一些技术已经应用于临床.迄今为止,超声弹性成像技术,按照施加激励的方式或检测方法的不同,可以大致分为静态/准静态压缩弹性成像^[4]、剪切波弹性成像^[1]、振动声成像^[5]和快速剪切波成像^[6]等.上述大部分成像方法应用的前提是首先假设所检测的组织是一个线弹性体,它们的主要缺陷是仅估计了组织的弹性,而忽略了黏性.实际上,人体大部分软组织都表现出黏弹性特征,忽略黏性,不但会造成组织弹性系数估计的偏差,而且易造成对组织病变特征判断不准确^[7].

为了弥补上述不足,Chen等人提出了剪切波频散超声振动成像技术(SDUV,Shearwave Dispersion Ultrasound Vibrometry)^[8],可以同时估计组织的剪切弹性模量与剪切黏性系数.通过超声聚焦,在组织内施加周期性的声辐射力,可使焦点处的组织产生简谐振动,从而引起背离激励点向外传播的平面剪切波.该剪切波含有多种谐振频率成分,且频率越大波速越大,满足Yamakoshi提出的各项同性均匀介质中平面剪切波与介质力学性质之间的关系模型^[9].因此,通过检测传播路径上不同位置不同频率剪切波的相位变化,估计剪切波波速,就可以拟合得到组织的弹性系数和黏性系数.

在SDUV方法中,剪切波相位估计的准确与否对剪切波波速的计算结果起着决定性的作用,而剪切波的相位需要从组织振动信号中提取出来.组织振动信号提取算法的原理都是基于组织产生相对运动时,超声回波在频域上会有相应的频移,通过获取该频移信息便可以提取出组织的振动信息.目前提取组织振动信号的方法主要有互相关估计法^[3]、正交解调法^[10]和互功率谱法^[11].互相关估计法需要确定最佳的时窗窗长和重叠率^[3],增加了算法提取效果的不确定性.同时,互相关估计法的算法复杂度高,计算效率低,在SDUV方法中不常使用,因此本文不做讨论.正交解调法通过频谱搬移,将待解调信号搬移到低频后滤除高频成分留下有用的信号,这样便可以获取相邻回波的相位变化以提取出组织的振动信号.而互功率谱法则是直接获取相邻回波互功率谱峰值处的相位,从而提取出组织的振动信号.尽管这两种方法都可以从原始超声回波中提取组织振动信号,但是应用于不同信噪比的超声回波信号时,它们的提取效果如何,方法的应用环境如何,以及算法的复杂度如何,都缺乏系统的研究和比较.

本文首先构造不同信噪比的参数化仿真超声回波信号模型,然后分别使用正交解调法和互功率谱法从超声回波信号中提取组织振动信号,进一步分离出组织振动信号的初始相位,比较两种方法的提取效果与计算效率,并对两种算法的实际应用予以讨论. 1 方法 1.1 正交解调法

由声辐射力在组织内产生的简谐振动可以由公式(1)表示^[5]:

其中,D₀是振动幅度;t_s是振动时间;φ_s是振动相位.当组织振动速度和振动频率分别远小于检测超声波的传播速度和频率时,振动信号的频谱可以用频率调制的模型表示^[12].因此,若检测探头的中心角频率为ω_f,包含有组织振动信息的反射回波可以表示为^[13]

其中,t_f是回波的采样时间;A(t_f,t_s)是回波的复包络;φ_f是回波的初相位.

其中,θ是多普勒角,默认为0;c是超声在介质中的纵向波速.在SDUV方法中,该模型(式(2))可以用来仿真组织振动时的超声回波检测信号^{[10, 12, 14]}.对超声回波信号r(t_f,t_s)做正交解调后,可以得到包含组织振动信息的同相分量式(4)和正交分量式(5):

其中φ₀是一个相位常量.组织振动信息就是利用相邻回波的相位差计算得到的.Zheng等人利用正交解调后相邻回波的同相分量和正交分量定义了复速度量^[10]:

其中,X为复速度量的实部;Y为复速度量的虚部.计算复速度量v(t_f,t_s)的复角,即相位信息,就可以提取出相邻回波的相位差,所以组织振动信号可以表示为

1.2 互功率谱法

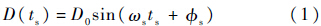
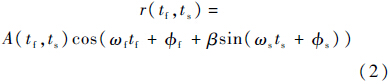
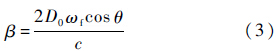
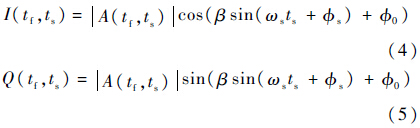
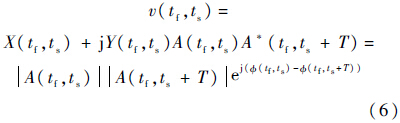
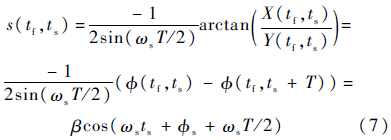
Hasegawa和Kanai提出计算相邻回波的互功率谱,使用互功率谱幅度最大处的频率作为实际的中心频率,在该频率处所对应的相位差作为相邻回波的相移^[11].若相邻回波r_n和r_n+1的功率谱分别是R_n(f)和R_n+1(f),则它们的互功率谱可以表示为

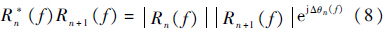
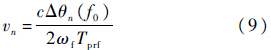
其中,Δθ_n(f)是相邻回波间的相移;*是复共轭运算.为了使得功率谱幅度在中心频率处达到最大值,所有回波运算前需要使用汉宁窗加窗.得到相邻回波的互功率谱后,可以找到谱幅度最大处的频率,分离出该频率所对应的互功率谱相位,即由组织位移引起的相位变化.组织的振动速度可以表示为

其中,f₀是互功率谱的中心频率;T_prf是检测脉冲的检测时间间隔;ω_f是检测探头的中心角频率;c是组织中的声速.对式(1)求导可以获得组织振动位移与振动速度间的关系.由于组织以ω_s谐振,所以,振动位移信号可以表示为

超声波在生物组织内传播时,会产生非线性效应,不同频率的超声波在组织的衰减系数不同,检测到的超声回波的中心频率可能会发生偏移.Kanai和Hasegawa指出,若不对超声回波的中心频率做矫正,会造成错误的结果^[11]. 2 实验

在FDA关于施加于人体的超声强度的标准要求下(I_SPTA<720 mW/cm²),施加于人体的声辐射力引起的组织振动幅度非常微弱,通常只能达到亚微米级^{[13, 14]}.本文设定振动信号的幅度为1 μm,是SDUV检测实验中振动信号幅度的典型值.其他仿真超声回波的参数设置如表 1所示.

表 1 仿真超声回波的参数设置 Table 1 Parameters of simulated ultrasound echoes

参数符号	物理意义	默认值
D₀	振动幅度	1 μm
φ_s	振动相位	45°
N	振动周期	5
ω_s	振动频率	2π×200 Hz
ω_f	超声频率	2π×9 MHz
F_s	采样频率	100 MHz
l_g	窗长度	1 mm
c	声速	1480 m/s

表选项

实际上,超声回波信号中会含有噪声,其信噪比主要由采集系统的噪声和组织的背向散射强度决定,若回波是反射信号,则信噪比能够达到30 dB以上,若回波主要来源于散射信号,信噪比可能会更低^[15].在SDUV检测中,噪声主要来自电子系统,因此,本文设定超声回波信号的噪声为高斯白噪声,信噪比20~50 dB,以比较不同信噪比下这两种方法提取振动信号的差异.每个信噪比的仿真回波取100组不同的数据,噪声的混入方法如式(11)所示.

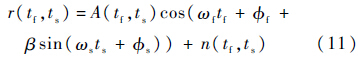
图 1是SNR_U=20 dB时的仿真超声回波,横轴是振动时间,纵轴是组织深度,从图中可以看到,仿真超声回波中包含了本文所设定的振动信息.

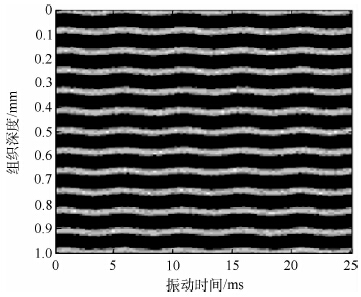图 1 仿真超声回波信号,SNR_U=20 dBFig. 1 Simulated ultrasound echo data with vibration,SNR_U=20 dB

图选项

在SDUV的算法中,振动信号相位提取的准确性直接影响剪切波波速的计算是否正确,剪切波波速计算的准确性又会影响黏弹性系数计算的准确性，因此,本文首先对如图 1所示的仿真回波分别使用正交解调法和互功率谱法提取振动信号,接着.利用Zheng等人提出的算法^[13],从提取出的振动信号中分离出振动相位,以比较正交解调法和互功率谱法这两种算法对提取出的振动信号的信噪比以及振动相位分离结果的影响.使用式(11)的模型是因为,无法确定真实超声回波信号中提取出的振动信号相位的真实值,从而无法对算法进行定量化的比较和分析.为了方便描述,下文中一些需要进行分析和比较的参数用表 2中的符号表示.

表 2 需要分析和比较的相关参数 Table 2 Symbols for the analyzed parameters

参数符号	物理意义
SNR_VD	超声回波信号的信噪比
SNR_VD	QDM提取出的振动信号的信噪比
SNR_VC	CSM提取出的振动信号的信噪比
φ_VD	QDM提取出的振动信号所分离出的振动相位
φ_VC	CSM提取出的振动信号所分离出的振动相位

表选项

3 结果

图 2为使用正交解调法、互功率谱法提取的振动信号和实验设定的振动信号,图中画出了2个周期.从图 2a中可以看到,当SNR_U=20 dB,互功率谱法可以很好地提取振动信号,提取效果优于正交解调法;当SNR_U=35 dB(图 2b),使用互功率谱法提取的振动信号仍然比使用正交解调法提取的振动信号更加接近于真实的振动信号,但是与图 2a比较,两者的差异减小.

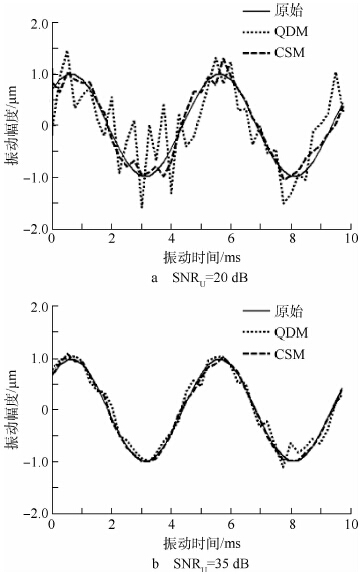图 2 QDM和CSM提取出的振动信号Fig. 2 Vibration signals extracted by QDM and CSM

图选项

定量化的分析,分别使用正交解调法和互功率谱法提取出的振动信号的信噪比如表 3所示.当SNR_U=20 dB时,SNR_VD和SNR_VC的均值和标准差分别为2.80±0.64 dB和14.00±0.64 dB.当SNR_U在20~50 dB的范围内,SNR_VC大约比SNR_VD要高11 dB.图 3是不同SNR_U下,正交解调法和互功率谱法提取出的振动信号所分离出的振动相位,实验设定的振动信号真实相位为45°.图中可以看到,随着SNR_U逐渐变大,φ_VC和φ_VD的标准差都逐渐减小,均值也更加接近45°.

表 3 不同SNR_U下,QDM和CSM法提取出的振动信号的信噪比(均值±标准差) Table 3 SNR (Mean±SD) of the vibration signalsextracted by QDM and CSM for various SNR_U

方法				信噪比/dB
方法	SNR_U=20 dB	SNR_U=25 dB	SNR_U=30 dB	SNR_U=35 dB	SNR_U=40 dB	SNR_U=45 dB	SNR_U=50 dB
QDM	2.80±0.64	7.75±0.67	12.79±0.67	17.75±0.67	22.72±0.68	27.86±0.68	32.67±0.51
CSM	14.00±0.64	19.11±0.67	24.13±0.64	29.12±0.60	34.13±0.64	39.02±0.67	43.81±0.64

表选项

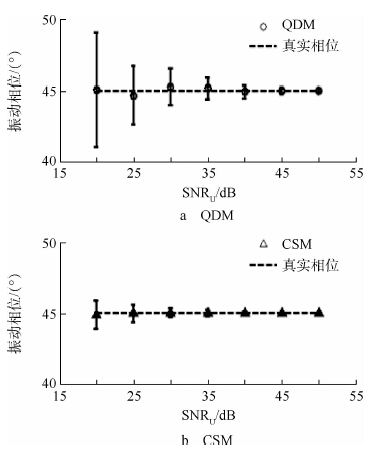图 3 不同SNR_U下,QDM和CSM法提取出的振动信号所分离出的振动相位Fig. 3 Estimated vibration phase using the vibration extracted by QDM and CSM for various SNR_U

图选项

表 4是φ_VD和φ_VC的结果.值得注意的是,SNR_U=20 dB时,φ_VD的标准差为3.97°,而φ_VC的标准差为1.00°,后者的结果明显优于前者;同时,相同SNR_U时,φ_VC比φ_VD更加接近真实的相位,标准差更小;SNR_U=20 dB时,φ_VD均值为45.16°,标准差为0.73°,而φ_VC均值为45.01°,标准差为0.22°,两者标准差都在1°以内.

表 4 不同SNR_U下,QDM和CSM法提取出的振动信号所分离出的振动相位(均值±标准差) Table 4 Estimated vibration phase (Mean±SD) of the vibration extracted by QDM and CSM for varions SNR_U

方法				振动相位/(°)
方法	SNR_U=20 dB	SNR_U=25 dB	SNR_U=30 dB	SNR_U=35 dB	SNR_U=40 dB	SNR_U=45 dB	SNR_U=50 dB
QDM	45.05±3.97	44.67±2.04	45.25±1.26	45.16±0.73	44.92±0.46	45.00±0.22	45.00±0.13
CSM	44.89±1.00	45.00±0.62	45.02±0.34	45.01±0.22	44.99±0.11	45.00±0.06	45.00±0.03

表选项

4 讨论

本文首先构造了不同信噪比的参数化仿真超声回波信号模型,然后分别使用正交解调法和互功率谱法从超声回波信号中提取振动信息,进一步分离出振动信号的初始相位.通过比较提取出的组织振动信号的信噪比和分离出组织振动信号相位的结果,研究了正交解调法和互功率谱法的组织振动信号提取效果.

从振动信号提取结果可以看出,与实验设定的振动信号比较,相同的SNR_U下,互功率谱法的提取效果优于正交解调法.由于初始设定的中心频率下超声回波信号中包含的振动信息被加入的噪声干扰,即相位发生了变化,而正交解调法是按照设定的中心频率提取超声回波信号的相位,因此不能有效跟踪噪声干扰后的回波信号中的实际中心频率,提取效果受到限制;而互功率谱法可以根据实际中心频率提取超声回波信号的相位,因此提取效果更好.随着SNR_U的提高,两种方法提取出的振动信号的信噪比也相应地提高,说明超声回波信噪比是影响组织振动信号提取效果的重要因素.

SNR_U≥35 dB时,SNR_VC大约比SNR_VD高约11 dB,但是相位φ_VC和φ_VD的标准差都在1°以内,结果非常接近.这是因为,当振动信号信噪比大于15 dB以后,本文所用的卡尔曼滤波算法分离出的振动相位的标准差小于1°,而SNR_U≥35 dB时,SNR_VC和SNR_VD均大于15 dB.运用SDUV检测组织黏弹性时,相邻检测点间距通常大于1/10的剪切波波长.也就是说,相邻检测点间的剪切波相位差大于36°,1°的标准差与其相比可以忽略不计,对于剪切波速度的估计没有太大影响.

正交解调法需要对回波信号低通滤波,若采用频域的方法,需要进行快速傅里叶变换和逆变换.互功率谱法需要对原始回波信号加窗,求取功率谱,并获取回波的相位信息,其算法复杂度比正交解调法要高,需要的计算时间更多.针对本文的实验,正交解调法提取出振动信号需要0.081 s,而互功率谱法提取出振动信号需要0.208 s(计算环境:Matlab R2011b,Intel E8200 2.66 GHz),互功率谱法的计算时间约为正交解调法的2.6倍. 5 结论

综上所述,当超声回波信号的信噪比小于35 dB时,应该使用互功率谱法提取组织的振动信号,以减小振动信号初始相位的提取误差.当超声回波的信噪比大于35 dB,两种算法在相同信噪比下提取出的信号所分离出的振动相位结果相近,对剪切波速度的估计没有太大影响,而互功率谱法算法复杂度比正交解调法高,因此,为了提高系统的实时性,应该选择正交解调法提取组织的振动信号.本研究的发现有助于提高SDUV方法的检测效率.

本文讨论了超声回波信号中的噪声为高斯白噪声的情况下,正交解调法和互功率谱法提取组织振动信号的差异.然而,临床上,超声回波信号可能被其他复杂的情况影响,如散射子混合产生的斑点效应,后续工作将会考虑对这些情况进行研究.

参考文献

[1]	Sarvazyan A P,Rudenko O V,Swanson S D,et al.Shear wave elasticity imaging:a new ultrasonic technology of medical diagnostics[J].Ultrasound in Medicine Biology,1998,24(9):1419-1435
	Click to display the text
[2]	Sarvazyan A,Hall T J,Urban M W,et al.An overview of elastography-an emerging branch of medical imaging[J].Current Medical Imaging Reviews,2011,7(4):255-282
	Click to display the text
[3]	Ophir J,Cespedes I,Ponnekanti H,et al.Elastography:a quantitative method for imaging the elasticity of biological tissues[J].Ultrasonic Imaging,1991,13(2):111-134
	Click to display the text
[4]	Ophir J,Cespedes I,Garra B,et al.Elastography:ultrasonic imaging of tissue strain and elastic modulus in vivo[J].European Journal of Ultrasound,1996,3(1):49-70
	Click to display the text
[5]	Fatemi M,Greenleaf J F.Ultrasound-stimulated vibro-acoustic spectrography[J].Science,1998,280(5360):82-85
	Click to display the text
[6]	Bercoff J,Tanter M,Fink M.Supersonic shear imaging:a new technique for soft tissue elasticity mapping[J].IEEE Transactionson Ultrasonics Ferroelectrics Frequency Control,2004,51(4):396-409
	Click to display the text
[7]	Salameh N,Peeters F,Sinkus R,et al.Hepatic viscoelastic parameters measured with MR elastography:correlations with quantitative analysis of liver fibrosis in the rat[J].Journal of Magnetic Resonance Imaging,2007,26(4):956-962
	Click to display the text
[8]	Chen S G,Urban M W,Pislaru C,et al.Shearwave dispersion ultrasound vibrometry(SDUV)for measuring tissue elasticity and viscosity[J].IEEE Transactionson Ultrasonics Ferroelectrics Frequency Control,2009,56(1):55-62
	Click to display the text
[9]	Yamakoshi Y,Sato J,Sato T.Ultrasonic imaging of internal vibration of soft tissue under forced vibration[J].IEEE Transactionson Ultrasonics Ferroelectrics Frequency Control,1990,37(2):45-53
	Click to display the text
[10]	Zheng Y,Greenleaf J F.Stable and unbiased flow turbulence estimation from pulse echo ultrasound[J].IEEE Transactionson Ultrasonics Ferroelectrics Frequency Control,1999,46(5):1074-1087
	Click to display the text
[11]	Hasegawa H,Kanai H.Improving accuracy in estimation of artery-wall displacement by referring to center frequency of RF echo[J].IEEE Transactionson Ultrasonics Ferroelectrics Frequency Control,2006,53(1):52-63
	Click to display the text
[12]	Huang S R,Lerner R M,Parker K J.On estimating the amplitudeof harmonic vibration from the Doppler spectrum of reflected signals[J].Journal of the Acoustical Society of America,1990,88(6):2702-2712
	Click to display the text
[13]	Zheng Y,Chen S G,Tan W,et al.Detection of tissue harmonic motion induced by ultrasonic radiation force using pulse-echo ultrasound and kalman filter[J].IEEE Transactionson Ultrasonics Ferroelectrics Frequency Control,2007,54(2):290-300
	Click to display the text
[14]	Urban M W,Greenleaf J F.Harmonic pulsed excitation and motion detection of a vibrating reflective target[J].Journal of the Acoustical Society of America,2008,123(1):519-533
	Click to display the text
[15]	Urban M W,Chen S G,Greenleaf J F.Harmonicmotion detection in a vibrating scattering medium[J].IEEE Transactionson Ultrasonics Ferroelectrics Frequency Control,2008,55(9):1956-1974
	Click to display the text

http://dx.doi.org/10.13700/j.bh.1001-5965.2013.0741
北京航空航天大学主办。

文章信息

蔡夕然, 樊璠, 李晓斐, 牛海军

Cai Xiran, Fan Fan, Li Xiaofei, Niu Haijun

SDUV方法中组织振动信号提取算法比较

Comparison of tissue vibration signal extraction algorithms in shearwave dispersion ultrasound vibrometry

北京航空航天大学学报, 2014, 40(12): 1761-1766

Journal of Beijing University of Aeronautics and Astronsutics, 2014, 40(12): 1761-1766.

http://dx.doi.org/10.13700/j.bh.1001-5965.2013.0741

文章历史

收稿日期：2014-01-08

网络出版日期: 2014-04-11

文章信息

文章历史

相关文章

工作空间