表1(Table 1)
面向高精度姿态确定的任务需求,星敏感器通常是必备的姿态确定设备,而星敏感器/陀螺组合测量更是成为了现代航天器普遍采用的敏感器配置模式.该配置模式结合了二者的优点,一方面利用星敏感器的高精度姿态信息对陀螺漂移进行修正补偿,另一方面陀螺作为惯性器件所具有的自主、实时、连续的特点可以弥补星敏感器在输出频率和易受外部环境影响上的不足,从而能够在长航时内获得高精度的定姿信息[1, 2].但是,在高动态条件下,恒星星光在星敏感器成像曝光时间内会拉长变形产生拖尾,有限的星光能量分散到更多的像元上,星像变得暗淡甚至淹没在背景噪声中,导致星图对比度和信噪比显著下降,影响星敏感器的观测精度,从而使惯性星光组合定姿的精度下降,甚至无法定姿.因此,星图拖尾是高动态条件下进行组合定姿亟待解决的一个关键问题.
星图拖尾是由于感光介质在曝光瞬间与被摄物之间存在相对运动造成的.传统的机械式、光学式、电子式像移补偿法[3, 4, 5]可以较好地抑制星图拖尾,但存在体积大、成本高、结构复杂、应用不灵活等缺陷.图像复原技术可以通过对星图进行后期处理消除拖尾,且成本低,算法比较成熟.常见的复原算法有逆滤波、维纳滤波、约束最小二乘、Richardson-Lucy算法[6, 7]等.逆滤波对噪声的影响比较敏感,约束最小二乘方法在噪声较强时复原效果较差,Richardson-Lucy方法则需要确定复原的迭代次数,且一般计算时间较长.鉴于星敏感器上的微处理器计算能力有限和星图拖尾成像过程中受噪声影响较大,可采用计算量小、抗噪性能优良的维纳滤波方法对拖尾星图进行复原处理.
为了解决高动态条件下惯性星光组合定姿的问题,本文提出了一种基于乘性扩展卡尔曼滤波(MEKF，Multiplicative Extended Kalman Filter)[8]的惯性星光深度组合姿态确定方法,利用星敏感器姿态信息修正陀螺误差,补偿陀螺漂移,同时利用陀螺输出信息估计星图拖尾的模糊参数,对产生拖尾的星图进行维纳滤波复原以提高观测精度.仿真实验表明该方法可以有效提高高动态条件下的惯性星光组合定姿的精度.
1 星敏感器角运动对成像的影响
星敏感器坐标系表示为O-XsYsZs,OZs为光轴,O-XsYs为星敏感器成像面阵.以绕Ys轴转动来讨论星敏感器角运动对成像的影响,如图 1所示,光轴向右旋转Δθ角度,导致星光成像从P点向P′点移动,星敏感器曝光时间很短,因此在曝光时间内光轴近似是匀速旋转,星光的能量均匀分布到PP′这段距离,星点像移量为[9]
 |
| 图 1 绕Ys轴转动产生的像移 Fig. 1 Image motion by rotation of Ys |
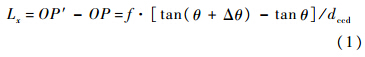
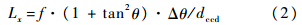
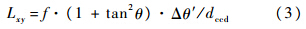
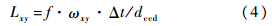
星敏感器绕Xs轴正向转动产生的像移为Ys的负方向,绕Ys正向转动产生的像移为Xs的正方向,当星敏感器同时绕Xs和Ys转动时,像移的方向如图 2所示,假设沿Xs正方向向上偏转角度为正,则像移方向可表示为
 |
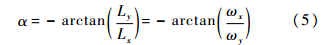
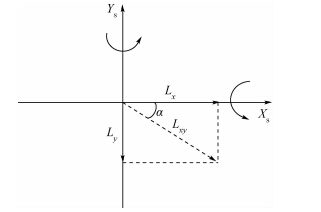| 图 2 同时绕Xs,Ys轴转动的像移方向 Fig. 2 Direction of image motion by rotation of Xs and Ys |
维纳滤波复原方法在频域中的表达式为
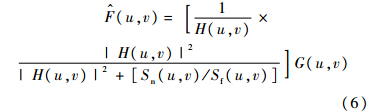
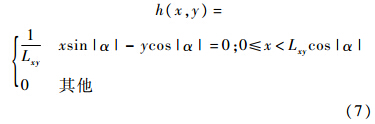
在实际应用中,由于不知道未退化图像的功率谱,常将图像信噪比设为一个常量k.而确定拖尾星图的模糊参数,只需要知道星敏感器在曝光时间内各轴的角度变化量,由陀螺进行估计得到.由于曝光时间一般很短,在这段时间内陀螺输出的角度变化量不存在积累误差,只含陀螺漂移和随机噪声,因而,模糊参数的估计误差很小. 3 惯性星光组合滤波器设计 3.1 系统状态方程及其线性化
一般情况下,陀螺测量的是航天器惯性系中角速度在体系中的分量,常用如下模型[10]:
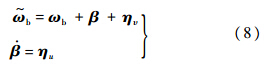
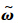b为陀螺的测量输出量;β为漂移量;ηυ和ηu分别为陀螺仪角度随机游走和陀螺仪漂移斜率随机游走,都是独立的零均值高斯白噪声过程.误差状态变量选取Δx≡[ΔΦT ΔβT]T,其中,Δβ为陀螺漂移的估计误差,ΔΦ是描述四元数估计误差的三分量矢量.系统的误差状态方程为
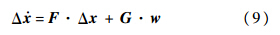
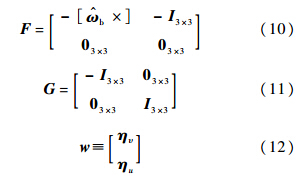
过程噪声w的谱密度矩阵为
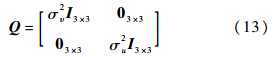
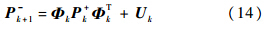
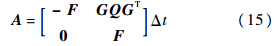
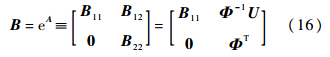
3.3 观测方程及其线性化
基于矢量观测的测量方程可写成[11]
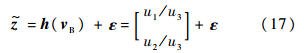
由于观测量不依赖于航天器姿态角速度和陀螺漂移,因此,总测量灵敏度矩阵可写为
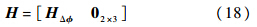
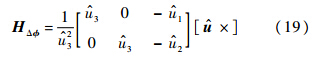
ε为观测噪声,假定它是均值为0的高斯白噪声,满足下式:
 |
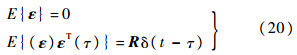
| 图 3 σs随像移量的变化曲线 Fig. 3 Variation of σs |
给出如下形式滤波更新方程:
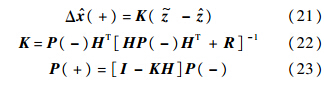
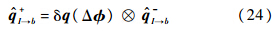
陀螺漂移的更新方程为
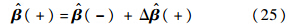
4 仿真结果
仿真流程如图 4所示,由陀螺输出的角速度信息一方面作为MEKF的输入,另一方面用来估计模糊参数,采用维纳滤波方法对拖尾星图进行复原,星图中星像的模拟采用高斯灰度扩散模型[13],然后进行星像质心提取,并采用基于K矢量查找技术[14]的星棱锥星图识别方法[15]对提取的星像进行识别,输出结果作为MEKF的观测量.MEKF输出误差状态量[Δ Δβ],其中Δ用来修正姿态误差,Δβ对陀螺漂移进行补偿,经过补偿后的陀螺输出对模糊参数的估计更加精确,从而进一步提高图像复原的效果.仿真参数设置如表 1所示.
 |
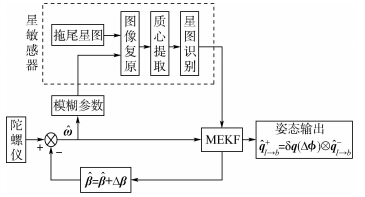| 图 4 仿真流程图 Fig. 4 Flow chart of simulation |
| 参数 | 取值 |
| 曝光时间/s | 0.2 |
| 成像面阵/像素 | 512×512 |
| 像元大小/μm | 15 |
| 焦距/mm | 36.54 |
| 视场/(°) | 12×12 |
| 星点高斯半径 | 0.45 |
| 星等阈值 | 5.5 |
陀螺角度随机游走συ/(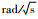 ) | 5×10-5 |
陀螺漂移斜率随机游走σu/(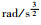 ) | 1×10-10 |
| 陀螺漂移β/((°)/h) | [5 5 5] |
| 维纳滤波加性噪声 | N(0,0.001) |
| k | 0.001 |
| 初始状态估值 | 06×1 |
| 初始方差σΔ/(°) | 5 |
| 初始方差σΔβ/((°)/h) | 5 |
| 初始姿态真值/(°) | [0 0 0] |
| 初始姿态估值/(°) | [3 3 3] |
| 真实角速度/(rad/s) | [-0.03 0.05 0] |
在高动态条件下会产生星图拖尾现象,使得星图的信噪比显著下降,部分暗星无法提取,导致星图中由于提取的星像少于3个或提取误差较大而无法识别的概率大大增加,在这种情况下,星敏感器不参与定姿滤波,无法修正陀螺漂移,由陀螺单独输出姿态,定姿精度较低.即使星图识别成功,由于星像质心提取误差的增加,同样会降低组合定姿的精度.更为严重的是,星像质心提取误差的增加会导致星图误匹配,使姿态误差急剧增加.图 5和图 6显示,高动态条件下组合定姿误差严重发散,在1500s的仿真时间内共发生了12次误匹配,已经不能进行姿态确定,而对星图进行复原后,无误匹配发生,且在仿真时间内都能提供高精度的定姿结果.
 |
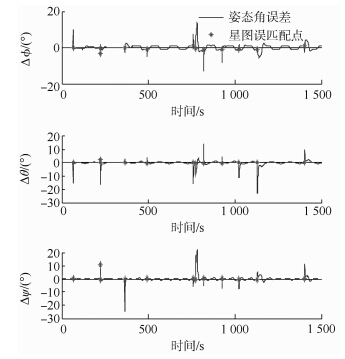| 图 5 组合定姿误差 Fig. 5 Estimation errors of attitude |
 |
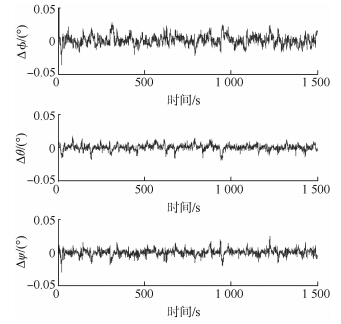| 图 6 复原后组合定姿误差 Fig. 6 Estimation errors of attitude after restoration |
图 7和图 8表明高动态条件下组合定姿方法的陀螺三轴漂移估计值都远远偏离了设定的真值,而进行星图复原后的组合定姿方法陀螺三轴漂移估计值最终都趋近于真值5(°)/h.这表明星图复原后星敏感器可以对陀螺漂移进行很好的补偿,且β2和β3的估计效果优于β1.另外,仿真参数中的3个欧拉角按321转序定义且估计初值均有3°的误差偏移.图 9给出了在高动态条件下,组合定姿方法和进行星图复原后的组合定姿方法前50s的姿态误差对比曲线,由图可知进行星图复原后的组合定姿方法对3个欧拉角初值估计误差的修正收敛更快、更平稳.仿真结果具体数据如表 2所示.
 |
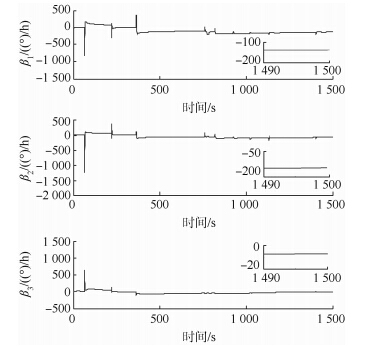| 图 7 陀螺漂移估计曲线 Fig. 7 Estimation curves of gyro drifts |
 |
| 图 8 复原后陀螺漂移估计曲线 Fig. 8 Estimation curves of gyro drifts after restoration |
 |
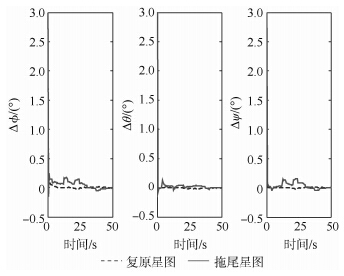| 图 9 仿真前50s组合定姿误差对比 Fig. 9 Comparison of attitude errors in first 50 seconds |
| 组合定姿模式 | 误匹配率/% | 星图识别率/% | 质心精度/像素 | β估计误差/((°)/h) | 定姿精度/(″) |
| 星图拖尾 | 0.4 | 33.6 | 0.8493 | [142.6 87.3 12.2] | 滤波发散 |
| 星图复原 | 0 | 88.0 | 0.1695 | [0.29 0.07 -0.06] | [15.83 8.87 9.34] |
本文提出了一种在高动态条件下进行惯性星光组合定姿的方法,其优势体现在以下3方面:
1) 在质心提取环节,可以有效地提高星图信噪比和星像的质心提取精度;
2) 在星图识别环节,降低了星点误匹配情况的发生,大大提高了星图识别率;
3) 在姿态确定环节,对姿态初值误差的修正收敛更快,滤波稳定后的定姿精度更高,对陀螺漂移的估计更加精确.
该方法满足了航天器在高动态条件下的定姿要求,具有一定的工程应用价值.
| [1] | 曾威,崔玉平,李邦清,等.惯性星光组合导航应用与发展[J].飞航导弹,2011(9):74-79 Zeng Wei,Cui Yuping,Li Bangqing,et al.The application and development of INS/Star integrated navigation[J].Aerodynamic Missile Journal,2011(9):74-79(in Chinese) |
| Cited By in Cnki (4) | |
| [2] | 谭汉清,刘垒.惯性星光组合导航技术综述[J].飞航导弹,2008(5):44-51 Tan Hanqing,Liu Lei.The overview of INS/Star integrated navigation[J].Aerodynamic Missile Journal,2008(5):44-51(in Chinese) |
| Cited By in Cnki (17) | |
| [3] | 李兴华.高分辨力空间摄影相机像移补偿控制技术研究[D].长春:中国科学院长春光学精密机械与物理研究所,2000 Li Xinghua.A study on image motion compensation control system in high-resolution space camera[D].Changchun:Changchun Institute of Optics,Fine Mechanics and Physics,Chinese Academy of Sciences,2000(in Chinese) |
| [4] | van Bezooijen R W H,Anderson K A,Ward D K.Performance of the AST-201 star tracker for the microwave anisotropy probe[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit.Monterey,California:AIAA,2002:1-11 |
| [5] | 李清军.面阵CCD相机像移补偿技术[J].计算机测量与控制,2008,16(12):1951-1953 Li Qingjun.IMC technology of the area scan CCD camera[J].Computer Measurement & Control,2008,16(12):1951-1953(in Chinese) |
| Cited By in Cnki (8) | |
| [6] | 刘微.运动模糊图像恢复算法的研究与实现[D].长春:中国科学院长春光学精密机械与物理研究所,2006 Liu Wei.The research on restoration algorithm of motion blur image and its realization[D].Changchun:Changchun Institute of Optics,Fine Mechanics and Physics,Chinese Academy of Sciences,2006(in Chinese) |
| [7] | 彭青建.运动模糊图像复原算法研究[D].成都:电子科技大学,2010 Peng Qingjian.Research of algorithm for restoration of motion blurred images[D].Chengdu:University of Electronic Science and Technology of China,2010(in Chinese) |
| [8] | 张力军.基于多视场星敏感器的航天器姿态确定方法研究[D].长沙:国防科学技术大学,2011 Zhang Lijun.Spacecraft attitude determination for multiple fields of view star sensors[D].Changsha:National University of Defense Technology,2011(in Chinese) |
| [9] | 吴小娟,王新龙.星图运动模糊及其复原方法[J].北京航空航天大学学报,2011,37(11):1338-1342 Wu Xiaojuan,Wang Xinlong.Motion blur of star image and restoration[J].Journal of Beijing University of Aeronautics and Astronautics,2011,37(11):1338-1342(in Chinese) |
| Cited By in Cnki (6) | |
| [10] | Crassidis J L.Sigma-point Kalman filtering for integrated GPS and inertial navigation[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit.San Francisco,California:AIAA,2005:1981-2004 |
| [11] | Markley F L.Attitude error representations for Kalman filtering[J].Journal of Guidance,Control,and Dynamics,2003,26(2):311-317 |
| Click to display the text | |
| [12] | 张金槐,蔡洪.飞行器试验统计学[M].长沙:国防科技大学出版社,1995:149-152 Zhang Jinhuai,Cai Hong.Experimental statistics of aircraft.Changsha:National University of Defense Technology Press,1995:149-152(in Chinese) |
| [13] | 王海涌,周文睿,赵彦武.简易高斯灰度扩散模型的误差分析及适用性研究[J].光学学报,2012,32(7):115-120 Wang Haiyong,Zhou Wenrui,Zhao Yanwu.Error analysis and applicability study on simplified Gaussian gray diffusion model[J].Acta Optica Sinica,2012,32(7):115-120(in Chinese) |
| Cited By in Cnki (4) | |
| [14] | Mortari D,Neta B.K-vector range searching techniques[J].Advances in the Astronautical Sciences,2000,1051:449-463 |
| [15] | Mortari D,Junkins J L,Samaan M A.Lost-in-space pyramid algorithm for robust star pattern recognition[C]//Guidance and Control Conference.Breckenridge,Colorado:AAS,2001,107:49-68 |
