结构固有频率分析在工程结构的动态特性分析和设计中具有重要的作用.然而,由于实际工程结构系统的复杂性,使得一些参数具有模糊性,如结构的几何参数、物理参数等,这就使得在结构固有频率分析时不得不考虑这些模糊参量对固有频率的影响.
模糊有限元法是有限元分析的一个新领域,它起始于20世纪90年代早期,Rao等人[1, 2]在研究了模糊有限元的理论和方程式之后,提出了用区间数求解模糊有限元方程的方法,并将其应用到工程系统的静态分析和振动分析中.郭书祥等人[3]基于模糊变量的区间表达和区间运算,导出了模糊变量的运算规则,并利用区间有限元理论,提出了结构模糊有限元静力控制方程的求解方法.吕恩琳[4]将区间数方程组解的定义与结构有限元平衡方程的力学意义结合起来,提出了结构的模糊有限元平衡方程的一种新解法.此外,国内外还有许多学者对模糊有限元做了一定的研究[5, 6, 7, 8, 9].
由于现有模糊有限元方法的局限性,目前在处理含有模糊参数的结构固有频率问题时,多采用基于区间理论的解法.邱志平等人[10]通过模糊数学中隶属度的性质,把振动结构的模糊参数表示成区间形式,得到区间形式的有限元平衡方程,再利用Taylor级数展开法求解特征值所在的区间集,最后通过模糊分解定理构造出相应的模糊解.索奇峰等人[11]基于区间运算和区间有限元理论,提出了用于求解模糊有限元自由振动方程的一阶Taylor级数展开算法.虽然区间方法具有应用面广的优点,但区间方法需要计算多个截集才能构造出相应的模糊解,计算量较大.
为了克服上述缺点,Yang等人[12]提出了模糊变分原理,并将该原理用于对模糊结构进行静态分析.该方法可以直接求解含有模糊参数的结构静态问题,不必将模糊参数转化为区间形式求解,而且可以直接得到相应的模糊解.由于模糊变分原理相对于传统的区间解法具有计算量少、求解简单的优点,所以本文将其推广到模糊结构的固有频率分析上.首先,基于模糊数学相关理论,在瑞利商变分中直接引入参数的模糊性,得到了结构固有频率问题的模糊变分原理.进而基于模糊变分原理,推导了模糊里兹法和模糊有限元法的计算公式.最后以模糊直梁为算例,说明了这两种方法的可行性和实用性.
1 线性峰型模糊数
对于普通集合,可以用特征函数来刻画,论域U中的一个元素是否属于U的某个子集A,只要看这个元素对集合A的特征函数值取1还是0.美国的控制专家Zadeh[13]推广了这个概念,提出用隶属函数来定义模糊集合.对于一个模糊集合,无法确定一个元素是否属于这个模糊集合,只能说它有多大程度属于这个模糊集合.这种从属程度本文用0,1之间的一个数来表示.这就是模糊集合的隶属函数.
定义1[14] 设在论域U上给定了一个映射μ:U→[0,1],则μ定义了U上的一个模糊子集,记为 .μ称为
.μ称为 的隶属函数,记为μ
的隶属函数,记为μ .
.
定义2[15] 有界闭模糊数 如果满足下列条件:
如果满足下列条件:
1)  的左右隶属函数LA(x)和RA(x)严格单调且连续,且0≤LA,RA≤1.
的左右隶属函数LA(x)和RA(x)严格单调且连续,且0≤LA,RA≤1.
2) 集合Ker 有且只有一个元素,
则称
有且只有一个元素,
则称 为峰型模糊数.
为峰型模糊数. 可记为
可记为
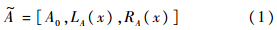
 的真值;LA(x),RA(x)称为模糊数
的真值;LA(x),RA(x)称为模糊数 的左、右隶属函数.当LA(x)和RA(x)为线性函数时,称
的左、右隶属函数.当LA(x)和RA(x)为线性函数时,称 为线性峰型模糊数,如图 1所示.这时有
为线性峰型模糊数,如图 1所示.这时有
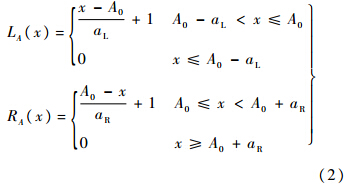
 的左右支集的长度.
的左右支集的长度.
 |
| 图 1 线性峰型模糊数 Fig. 1 Image motion by rotation of Ys |
由工程师或专家给出模糊数 的真值A0及其可能的变化范围[Al,Ah]后,可利用下式求出aL,aR:
的真值A0及其可能的变化范围[Al,Ah]后,可利用下式求出aL,aR:
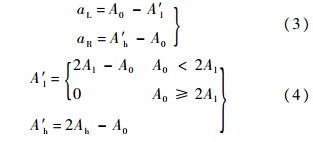
结构的固有频率是结构参数的函数,当一个结构的几何参数、物理参数是模糊数时,则结构的固有频率就是模糊数.具有模糊参数的结构的瑞利商变分可表示为

 max是模糊结构弹性势能的最大值;
max是模糊结构弹性势能的最大值; 是模糊结构的动能系数.
是模糊结构的动能系数.


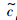 ijkl表示模糊弹性张量;
ijkl表示模糊弹性张量;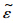 ij表示模糊应变张量;
ij表示模糊应变张量; 表示模糊密度;
表示模糊密度;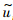 i表示模糊位移矢量.
i表示模糊位移矢量.
令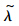 =ω~2,则有
=ω~2,则有
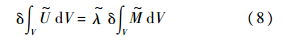
设模糊场 包含了结构的所有模糊参量,其展开式如下:
包含了结构的所有模糊参量,其展开式如下:


 1,
1, 2,…,
2,…, r)T是真值为零的模糊摄动量.
r)T是真值为零的模糊摄动量.
由于模糊量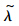 是模糊场
是模糊场 的函数,因此,
的函数,因此,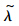 可以在X0处通过Taylor级数进行二阶摄动展开.
可以在X0处通过Taylor级数进行二阶摄动展开.

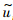 ,
,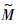 也可以类似地展开.将展开式代入式(8)中,利用摄动法可得式(12)~式(14).
也可以类似地展开.将展开式代入式(8)中,利用摄动法可得式(12)~式(14).零阶:

一阶:

二阶:

分别对(12)~式(14)进行变分,并令 i=-
i=-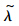

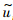 i,可得式(15)~式(17).
i,可得式(15)~式(17).
零阶:

一阶:

二阶:

由上述方程可知,二阶摄动展开式的变分极值条件包含了零阶和一阶的变分极值条件,因此只需要利用二阶摄动展开式的变分极值条件即可得到全部的控制方程.
3 模糊里兹法
如图 2所示的等截面弹性简支直梁,设其弹性模量E和密度ρ是模糊量.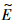 的真值为E0,可能变化范围是[El,Eh];
的真值为E0,可能变化范围是[El,Eh]; 的真值为ρ0,可能变化范围是[ρl,ρh].根据式(3)和式(4),可计算出
的真值为ρ0,可能变化范围是[ρl,ρh].根据式(3)和式(4),可计算出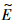 和
和 的左、右支集长度eL,eR和ρL,ρR.为了简化计算,此处取左、右支集长度相等,即
的左、右支集长度eL,eR和ρL,ρR.为了简化计算,此处取左、右支集长度相等,即

 |
| 图 2 等截面弹性简支直梁 Fig. 2 Simply supported elastic beam with uniform cross section |
梁的模糊瑞利商变分如下所示:

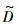 =
=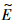 I;
I;
式(19)的二阶摄动展开式为



从上述列式中可以解出结构第i阶固有频率对应的λi0,λi,m,λi,mn,将其代入式(11),根据线性峰型模糊数的运算法则[12],即可得到结构第i阶模糊固有频率表达式:




4 模糊有限元法
将结构离散成有限个单元体,对单元位移场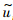 进行插值:
进行插值:

 i为
i为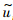 在节点i上的值;N为形函数矩阵.
在节点i上的值;N为形函数矩阵.
应变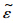 与
与 满足下式:
满足下式:

由式(7)和式(8)可得


对其进行二阶摄动展开,由模糊变分原理可知,第2阶摄动展开式包含全部的控制方程,因此,只需考虑第2阶摄动展开式.利用变分极值条件,可得到下列方程.
零阶:


一阶:


二阶:



将上述列式中解出的λi0,λi,m,λi,mn代入式(11)中,根据线性峰型模糊数的运算法则[12],即可得到结构第i阶固有频率的模糊有限元解.
5 数值算例
对于图 2所示的等截面弹性简支直梁,取杨氏模量E和密度ρ为模糊量,其真值分别为E0,ρ0,二者的可能变化范围分别是[0.8E0,1.2E0],[0.9ρ0,1.1ρ0].利用模糊里兹法,可求得结构第i阶模糊固有频率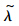 i的ξ-截集为
i的ξ-截集为

对于等截面弹性简支直梁,其第i阶固有频率的解析解为


表 1~表 3给出在不同ξ-截集下,采用模糊解析法(FAM,Fuzzy Analytical Method)、模糊有限元法(FFEM,Fuzzy Finite Element Method)、模糊里兹法(FRM,Fuzzy Ritz Method)所计算的梁结构前三阶固有频率的结果以及模糊有限元法、模糊里兹法相对于模糊解析法的计算误差,其中各阶固有频率计算结果的乘子为E0I/(ρ0Al4).并且在模糊有限元法求解时,将梁结构离散成了6个三次直梁单元.
从表 1~表 3列出的梁前三阶固有频率的计算结果中可以看出,当置信水平为1时,模糊结构退化为确定性结构,其固有频率也变为一个确定值;随着模糊参量的置信水平的降低,结构的模糊性增大,相应的其固有频率的变化范围增大;当置信水平取为0.8时,以一阶固有频率的里兹解为例,其最大值超出了确定性计算所得结果的12.48%,这说明对结构固有频率进行模糊分析是很有必要的;模糊里兹法和模糊有限元法都可以直接得到各阶固有频率的ξ-截集下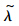 iξ的表达式,方便得出不同的置信水平下的结构固有频率的变化范围.
iξ的表达式,方便得出不同的置信水平下的结构固有频率的变化范围.
| ξ | FAM | FFEM | FFEM误差/% | FRM | FRM误差/% |
| 1 | 97.409 | 97.419 | 0.010 | 97.409 | 0.000 |
| 0.9 | [91.679,103.373] | [91.457,103.381] | 0.242,0.008 | [91.448,103.371] | 0.253,0.002 |
| 0.8 | [86.170,109.585] | [85.261,109.577] | 1.054,0.007 | [85.252,109.566] | 1.064,0.018 |
| 0.7 | [80.868,116.062] | [78.832,116.007] | 2.518,0.048 | [78.823,115.995] | 2.528,0.058 |
| 0.6 | [75.763,122.820] | [72.168,122.670] | 4.744,0.122 | [72.161,122.658] | 4.754,0.132 |
| ξ | FAM | FFEM | FFEM误差/% | FRM | FRM误差/% |
| 1 | 1558.5 | 1561.1 | 0.162 | 1558.5 | 0.000 |
| 0.9 | [1466.9,1654.0] | [1465.5,1656.6] | 0.091,0.160 | [1463.2,1653.9] | 0.253,0.002 |
| 0.8 | [1378.7,1753.4] | [1366.2,1755.9] | 0.904,0.144 | [1364.0,1753.1] | 1.064,0.018 |
| 0.7 | [1293.9,1857.0] | [1263.2,1858.9] | 2.370,0.104 | [1261.2,1855.9] | 2.528,0.058 |
| 0.6 | [1212.2,1965.1] | [1156.4,1965.7] | 4.600,0.029 | [1154.6,1962.5] | 4.754,0.132 |
| ξ | FAM | FFEM | FFEM误差/% | FRM | FRM误差/% |
| 1 | 7890.1 | 7952.5 | 0.791 | 7890.1 | 0.000 |
| 0.9 | [7426.0,8373.2] | [7465.8,8439.2] | 0.536,0.789 | [7407.3,8373.0] | 0.253,0.002 |
| 0.8 | [6979.7,8876.4] | [6960.1,8945.0] | 0.282,0.773 | [6905.4,8874.8] | 1.064,0.018 |
| 0.7 | [6550.3,9401.0] | [6435.2,9469.9] | 1.757,0.733 | [6384.7,9395.6] | 2.528,0.058 |
| 0.6 | [6136.8,9948.4] | [5891.0,10014] | 4.001,0.658 | [5845.0,9935.3] | 4.754,0.132 |
通过对表 1~表 3中模糊有限元法和模糊里兹法的计算误差进行对比分析可以看出,该算例中两种方法计算所得的结构固有频率的上界误差都小于相应下界误差;模糊有限元法的误差是随着置信水平和固有频率阶次的不同而变化的,模糊里兹法的误差却只与置信水平有关,与固有频率的阶次无关;随着置信水平的降低,两种方法的下界误差都在逐渐增大;当置信水平ξ≥0.8时,在各阶固有频率的计算中,模糊有限元法的最大误差为1.054%,模糊里兹法的最大误差为1.064%;即使将置信水平降到ξ=0.6,两种方法的最大误差也都不超过4.8%,可见本文所提的两种方法都具有较高的计算精度.
下面以一阶固有频率为例,讨论本文所提方法相对于传统区间解法的优势.
采用本文所提的模糊里兹法和模糊有限元法,都可以直接得到一阶固有频率的模糊解:

若采用文献[10]中所提的基于区间理论的模糊有限元法求解该问题,首先要通过ξ-截集方法将模糊参数转换成多个区间参数.对于该问题中的模糊参数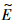 和
和 ,可以转成表 4所示的6组区间参数.
,可以转成表 4所示的6组区间参数.
| ξ | E | ρ |
| 1 | E0 | ρ0 |
| 0.8 | [0.92E0,1.08E0] | [0.96ρ0,1.04ρ0] |
| 0.6 | [0.84E0,1.16E0] | [0.92ρ0,1.08ρ0] |
| 0.4 | [0.76E0,1.24E0] | [0.88ρ0,1.12ρ0] |
| 0.2 | [0.68E0,1.32E0] | [0.84ρ0,1.16ρ0] |
| 0 | [0.60E0,1.40E0] | [0.80ρ0,1.20ρ0] |
之后,将梁结构离散成6个三次直梁单元,对表 4中的6组区间参数分别进行区间运算,可以得到如表 5所示的每个ξ-截集下的区间解.
| ξ | λ |
| 1 | 97.419E0I/(ρ0Al4) |
| 0.8 | [85.261,109.577]E0I/(ρ0Al4) |
| 0.6 | [72.168,122.670]E0I/(ρ0Al4) |
| 0.4 | [58.140,136.699]E0I/(ρ0Al4) |
| 0.2 | [43.176,151.662]E0I/(ρ0Al4) |
| 0 | [27.277,167.561]E0I/(ρ0Al4) |
最后,将得到的6组区间解,通过模糊分解定理构造出如图 3所示的模糊解,其中固有频率的乘子为E0I/(ρ0Al4).
 |
| 图 3 由区间解构造的模糊解 Fig. 3 Fuzzy result constructed by interval results |
因此,采用传统的区间解法,要先将模糊参数转化为多组区间参数,之后通过多次区间运算得到区间解,最后由区间解构造出相应的模糊解.构造所得的模糊解的精确性与所取ξ-截集个数有关,截集个数越多,所构造的模糊解越精确,但同时需要进行区间计算的次数就越多,计算量也就越大.而使用本文所提方法,只需要进行一次模糊运算就可以得到问题的模糊解.因此,本文所提方法可以很大程度上减少计算量.
6 结 论
通过本文的理论推导及数值算例的验证,可以得到以下3个重要结论:
1) 提出了结构固有频率问题的模糊变分原理;
2) 基于模糊变分原理,推导了可以直接得到问题模糊解的模糊里兹法和模糊有限元法;
3) 所提方法与传统的区间解法相比,减少了计算量,提高了计算效率.
因此,本文提出的方法为分析模糊结构的固有频率提供了一种简单而有效的途径.
| [1] | Rao S S,Sawyer J P.A fuzzy element approach for the analysis of imprecisely-defined system[J].AIAA Journal,1995,33(12):2364-2370 |
| Click to display the text | |
| [2] | Chen L,Rao S S.Fuzzy finite-element approach for the vibration analysis of imprecisely-defined systems[J].Finite Elements in Analysis and Design,1997,27(1):69-83 |
| Click to display the text | |
| [3] | 郭书祥,吕震宙,冯立富.模糊运算和模糊有限元静力控制方程的求解[J].应用数学和力学,2002,23(9):936-942 Guo Shuxiang,Lü Zhenzhou,Feng Lifu.Fuzzy arithmetric and solving of the static governing equations of fuzzy finite element method[J].Applied Mathematics and Mechanics,2002,23(9):936-942(in Chinese) |
| Cited By in Cnki (41) | |
| [4] | 吕恩琳.结构模糊有限元平衡方程的一种新解法[J].应用数学和力学,1997,18(4):361-365 Lü Enlin.A new solution to structural fuzzy finite element equilibrium equations[J].Applied Mathematics and Mechanics,1997,18(4):361-365(in Chinese) |
| Cited By in Cnki (46) | |
| [5] | 林育梁.模糊有限单元法的运算方法探讨[J].岩土力学,1996,17(2):81-87 Lin Yuliang.Exploring the calculating method of fuzzy finite element method[J].Rock and Soil Mechanics,1996,17(2):81-87(in Chinese) |
| Cited By in Cnki (5) | |
| [6] | 禹智涛,吕恩琳,王彩华.结构模糊有限元平衡方程的一种解法[J].重庆大学学报:自然科学版,1996,19(1):53-58 Yu Zhitao,Lü Enlin,Wang Caihua.A method of solving the structural fuzzy finite element equilibrium equations[J].Journal of Chongqing University:Natural Science Edition,1996,19(1):53-58(in Chinese) |
| Cited By in Cnki (47) | |
| [7] | Valliappan S,Pham T D.Fuzzy finite element analysis of a foundation on an elastic soil medium[J].International Journal for Numerical and Analytical Methods in Geomechanics,1993,17(11):771-789 |
| Click to display the text | |
| [8] | Akpan U O,Koko T S,Orisamolu I R,et al.Practical fuzzy finite element analysis of structures[J].Finite Elements in Analysis and Design,2001,38(2):93-111 |
| Click to display the text | |
| [9] | Behera D,Chakraverty S.Fuzzy finite element analysis of imprecisely defined structures with fuzzy nodal force[J].Engineering Applications of Artificial Intelligence,2013,26(10):2458-2466 |
| Click to display the text | |
| [10] | 邱志平,刘正权.含模糊参数振动系统的Taylor级数展开法[J].北京航空航天大学学报,2005,31(12):1342-1346 Qiu Zhiping,Liu Zhengquan.Taylor series expansion method for vibration system with fuzzy parameters[J].Journal of Beijing University of Aeronautics and Astronautics,2005,31(12):1342-1346(in Chinese) |
| Cited By in Cnki (4) | |
| [11] | 索奇峰,谢尚英.桥梁结构动力特性的模糊有限元分析[J].公路交通科学,2010,27(4):56-59 Suo Qifeng,Xie Shangying.Analysis of dynamic property of bridge structures using fuzzy finite element method[J].Journal of Highway and Transportation Research and Development,2010,27(4):56-59(in Chinese) |
| Cited By in Cnki (3) | |
| [12] | Yang L F,Li Q S,Leung A Y T,et al.Fuzzy variational principle and its applications[J].European Journal of Mechanics-A/Solids,2002,21(6):999-1018 |
| Click to display the text | |
| [13] | Zadeh L A.Fuzzy sets[J].Information and Control,1965,8:338-353 |
| Click to display the text | |
| [14] | 刘林,曹艳平,王婷.应用模糊数学[M].2版.西安:陕西科学技术出版社,2008:20-48 Liu Lin,Cao Yanping,Wang Ting.Applied fuzzy mathematics[M].2nd ed.Xi'an:Shanxi Science and Technology Press,2008:20-48(in Chinese) |
| [15] | 杨绿峰.模糊随机有限元法及其应用[D].武汉:武汉工业大学,1998 Yang Lüfeng.Fuzzy stochastic finite element methods and their applications[D].Wuhan:Wuhan University of Technology,1998(in Chinese) |




