Download PDF  
文章快速检索  
  高级检索
引用本文
梁祖典, 燕瑛, 张涛涛, 李剑峰, 孟祥吉, 廖宝华. 复合材料单搭接胶接接头试验研究与数值模拟[J]. 北京航空航天大学学报, 2014, 40(12): 1786-1792
Liang Zudian, Yan Ying, Zhang Taotao, Li Jianfeng, Meng Xiangji, Liao Baohua. Experimental investigation and numerical simulation of composite laminate adhesively bonded single-lap joints[J]. Journal of Beijing University of Aeronautics and Astronsutics, 2014, 40(12): 1786-1792.
复合材料单搭接胶接接头试验研究与数值模拟
梁祖典1, 燕瑛1, 张涛涛1, 李剑峰1, 孟祥吉1, 廖宝华2    
1. 北京航空航天大学 航空科学与工程学院, 北京 100191;
2. 成都飞机设计研究所, 成都 610041
收稿日期:2014-01-13; 网络出版日期: 2014-06-09
基金项目：国家973计划资助项目(2011CB606105).
作者简介: 梁祖典(1988-),男,山东平度人,硕士生,liangzudian@163.com.
摘要：针对不同搭接长度和不同被胶接件厚度的T300/QY8911层合板单搭接胶接接头进行了试验研究和数值模拟.建立了不同试验参数下的三维有限元模型,基于Hashin准则和连续介质损伤力学(CDM,Continuum Damage Mechanics)预测层合板面内损伤的起始和演化,应用黏聚区模型(CZM,Cohesive Zone Model)模拟层合板的分层损伤及胶层的失效.系统地研究了接头在不同参数下的失效模式、破坏形貌和极限载荷等的变化,模拟结果与试验吻合良好,验证了有限元分析模型的有效性.通过对接头的破坏形貌和应力分布进一步分析发现,胶接连接的失效模式和极限载荷均与胶接长度和被胶接件厚度有关;模拟接头胶接区在不同加载时刻的应力分布变化,反映了胶接连接在拉伸载荷下的破坏起始和演化过程.
关键词： 复合材料层合板     单面搭接     渐进损伤     黏聚区模型     失效模式     应力分析    
Experimental investigation and numerical simulation of composite laminate adhesively bonded single-lap joints
Liang Zudian1, Yan Ying1, Zhang Taotao1, Li Jianfeng1, Meng Xiangji1, Liao Baohua2     
1. School of Aeronautic Science and Engineering, Beijing University of Aeronautics and Astronautics, Beijing 100191, China;
2. Chengdu Aircraft Design and Research Institute, Chengdu 610041, China
Abstract:Both experimental tests and finite element method (FEM) simulation were implemented to investigate T300/QY8911 composite laminate single-lap joints with various single-lap length and adherend thickness. 3D finite element models of the joints under various experimental parameters were established. The damage initiation and progressive damage evolution of laminates were predicted based on Hashin criterion and continuum damage mechanics (CDM). The delamination of laminates and the failure of adhesive were simulated by cohesive zone model (CZM). The change of failure modes, damage contours and ultimate-loads of adhesively bonded single-lap joints were investigated systematically under various parameters. The FEM simulation accords well with experimental results which proves the efficiency of FEM simulation. Damage contours and stress distribution of the joints show that the failure modes and ultimate-loads of single-lap joints are both related to the single-lap length and adherend thickness. Simulation of the stress distribution of joints at different loading points reflects damage initiation and evolution of adhesively bonded single-lap joints under extension loads.
Key words: composite laminates     single-lap joints     progressive damage     cohesive zone models     failure modes     stress analysis    

复合材料结构设计力图实现结构的整体性,但由于工程实际需要又须离型制造,再进行装配,所以复合材料之间的连接必不可少.相较于传统的机械连接,胶接连接具有结构重量轻、连接效率高、破损安全性好、减振及绝缘性能好、能获得光滑气动外形等优点,越来越广泛地应用于复合材料构件间的连接.再者,在研究复合材料结构的胶接修补时,一般先对其相应的胶接接头的力学性能进行研究.单面搭接由于工艺简便,操作容易,经济性好,在工程上应用十分广泛,因此对复合材料单搭接接头的研究越来越引起学者们的重视.

与金属的胶接相比,复合材料具有各向异性、层间强度低等特点,其胶接行为相当复杂.胶接失效模式与搭接长度、被胶接件厚度、铺层方式等因素密切相关.自20世纪30年代开始,国内外学者[1,2,3,4,5,6]便对胶接连接理论进行了研究.近年来,有限元分析方法在胶接连接分析中逐渐得到应用[7,8,9,10,11].Groth等人[12]应用有限元方法研究了与接头奇异强度因子相关的断裂准则;Wahab等人[13]根据热力学原理得到了一种损伤演化准则,通过损伤变量来控制损伤演化过程;De Moura等人[14]讨论了黏聚区模型和连续损伤模型预测胶接接头力学行为的适用性;Anyfantis等人[15]提出了一种新的T-S准则来模拟韧性胶层的混合破坏模式.但是对于接头在不同参数下的失效模式、破坏形貌和极限载荷等的变化缺少可靠有效的有限元模拟,本文针对T300/QY8911层合板单搭接接头进行了上述研究,对其工程应用具有指导意义.

本文首先开展了不同参数下层合板胶接连接的拉伸强度试验研究,分析其随胶接长度、被胶接件厚度的变化而发生不同拉伸失效的机理;其次,建立了层合板单搭接接头的三维有限元模型,基于Hashin准则和连续介质损伤力学(CDM,Continuum Damage Mechanics)预测层合板的面内损伤起始和演化,应用黏聚区模型(CZM,Cohesive Zone Model)模拟层合板的分层损伤及胶层的失效.通过和试验结果的对比,验证了有限元模型的有效性;最后,基于数值模拟研究胶接连接件的应力分布,进一步分析胶接连接在拉伸过程中的破坏过程. 1 试验研究 1.1 试验件及试验方法

试验件示意图如图 1a所示.为研究不同几何参数下接头的失效模式和极限载荷,试验件分为6组,每组5件,长×宽均为170 mm×25 mm,各组试验件的搭接长度Ld和铺层方式如表 1所示.层合板采用T300/QY8911预浸料经加压固化制成,固化后预浸料的单层厚度为0.12 mm;胶层材料采用厚度为0.12 mm的J116B型胶膜,通过对试验件进行密封包装、抽真空、烘箱中加热固化,实现接头的胶接行为.为减小载荷偏心对试验的影响,并避免在加载过程中产生端部损伤,在层合板两端采用正交铺层的玻璃纤维增强板作为加强片,长度均为50 mm.试验使用INSTRON 8801伺服液压测试系统进行加载,如图 1b所示.

图 1 试验件示意图与INSTRON 8801测试机Fig. 1 Test samples sketch and INSTRON 8801 equipment
图选项

表 1 单面搭接试验件Table 1 Test samples of single-lap joints
试验件编号 Ld/mm 铺层方式
上面板 下面板
SL-2.5-0.962.5[45/0/-45/90]s[-45/0/45/90]s
SL-5-0.965[45/0/-45/90]s[-45/0/45/90]s
SL-10-0.9610[45/0/-45/90]s[-45/0/45/90]s
SL-20-0.9620[45/0/-45/90]s[-45/0/45/90]s
SL-10-1.9210[45/0/-45/90]2s[-45/0/45/90]2s
SL-10-3.8410[45/0/-45/90]4s[-45/0/45/90]4s

表选项
1.2 试验结果与讨论

如图 2所示,单搭接胶接接头的失效模式主要有3种:模式A，胶层剪切失效;模式B，层合板的铺层剥离及纤维的撕裂与拉断;模式C，二者的混合破坏模式.

图 2 单搭接接头的3种失效模式Fig. 2 Three failure modes of single-lap joints
图选项

各组试验件失效模式的统计结果如表 2所示.

表 2 不同试验参数下接头的失效模式Table 2 Failure modes under different test parameters
搭接长度/mm被胶接件厚度/mm失效模式
2.50.96几乎全为模式A
50.9650%模式B+50%模式C
100.96几乎全为模式B
200.96几乎全为模式B
101.9290%模式B+10%模式C
103.8450%模式B+50%模式C

表选项

对于被胶接件厚度为0.96 mm的接头,当搭接长度较小时,接头失效模式主要为A;随着搭接长度的增大,失效变为混合模式C;当搭接长度增大到一定长度时,失效模式主要为B.

对于搭接长度为10 mm的接头,当被胶接件厚度较小时,接头处附加弯矩较小,接头失效模式主要为B;随着被胶接件厚度的增大,接头处附加弯矩逐渐增大,引起部分胶层也发生失效,失效模式逐渐变为模式C;被胶接件厚度越大,越容易引发胶层失效,失效区域也逐渐扩大. 2 数值分析模型 2.1 面内损伤模型

基于Hashin准则,并结合连续介质损伤力学建立面内损伤模型,采用渐进损伤分析理论来模拟面内损伤的起始及演化.

Hashin准则考虑了4种不同模式的损伤失效机制:纤维拉伸断裂、纤维压缩屈曲、基体在横向拉伸和剪切下的断裂、基体在横向压缩和剪切下的压溃.具体表达形式如下.

纤维拉伸(σ11≥0):

纤维压缩(σ11≤0):

基体拉伸(σ22≥0):

基体压缩(σ22≤0):

其中,XT,XC,YT,YC,SL,ST分别表示纵向拉伸强度、纵向压缩强度、横向拉伸强度、横向压缩强度、面内剪切强度、横向剪切强度;α表示剪切应力对于纤维拉伸失效贡献的系数; σ=Mσ为有效应力张量,表征损伤处的真实承载能力和应力水平,用于评估损伤的起始,其中σ为真实应力,M为损伤算子:

其中df,dm,ds分别为表征纤维、基体、剪切损伤的内在损伤变量,由与4种损伤模式相对应的失效系数推导得出;在损伤发生之前,损伤算子矩阵M为单位矩阵,因此σ=σ.当材料至少在一种模式下发生损伤并演化后,损伤算子在其他模式的损伤起始判据中的影响逐渐增大.

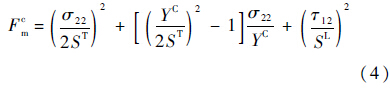
基于连续介质损伤力学(CDM,Continuum Damage Mechanics)的渐进损伤理论采用损伤变量来描述Hashin准则的各种失效模式,假定材料在损伤发生前是线弹性的,损伤起始后材料的刚度逐渐退化最终导致失效,损伤演化的过程基于能量耗散理论.

材料发生损伤后,其本构关系为

式中，D=1-(1-df)(1-dm)ν12ν21; ε为应变;Cd为材料的损伤弹性矩阵;E1,E2分别为面内纤维方向和垂直于纤维方向的弹性模量;G为剪切模量;ν12和ν21为泊松比. 2.2 层间损伤与胶层损伤模型

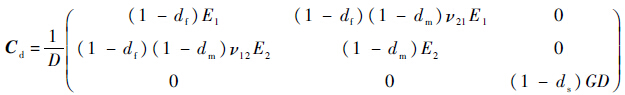
基于黏聚区模型建立层间损伤和胶层损伤模型.层合板层间界面采用零厚度的内聚力单元,胶层采用有厚度的内聚力单元.基于牵引-分离准则(traction-separation law)的内聚力单元的本构模型有多种形式,主要体现在材料退化曲线上,本文采用双线性本构模型(如图 3所示).假设单元的初始厚度为T0,对于单纯的Ⅰ型、Ⅱ型、Ⅲ型开裂模式,单元应变ε与张开位移δ之间的关系为

图 3 内聚力单元的双线性本构模型Fig. 3 Bilinear constitutive model of cohesive element
图选项

单元未发生损伤时,其线弹性本构关系为

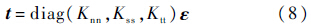
其中,t=(tn,ts,tt)T包含正应力和两个剪应力分量;Knn,Kss和Ktt则是对应的刚度系数.

内聚力单元的损伤起始采用二次名义应力准则来判断:

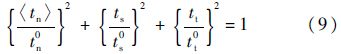
其中tn0,ts0和tt0分别表示内聚力单元的法向强度和两个方向的剪切强度,当单元各方向的名义应力比的平方和等于1时,开始发生损伤,此时,δ=δ0.当内聚力单元发生损伤后,其应力-应变关系变为

其中D为损伤系数,0≤D≤1.D=0表示材料未发生损伤;D=1表示材料完全破坏,此时,δ=δf.材料的软化过程和最终失效位移δf由单元的临界应变能释放率GC来控制,GC的值等于图 3中应力-位移曲线下的面积.

由于内聚力单元的破坏往往并不是单纯的Ⅰ型、Ⅱ型、Ⅲ型开裂,而是发生混合模式的开裂,因此引入混合模式下的等效张开位移δm:

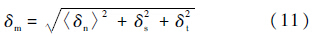
混合模式下的临界应变能释放率通过B-K(Benzeggagh-Kenane)断裂准则来计算:

其中,GS=Gs+Gt;GT=Gn+Gs;η为与材料有关的参数,对于碳纤维环氧复合材料,η=1~2,本文取η=1.45. 2.3 有限元模型

基于前述面内损伤模型及层间损伤和胶层损伤模型,在大型有限元软件平台ABAQUS中建立了单搭接接头的三维有限元模型,选取中间有效区域进行等效建模.边界条件等效为接头一端面的结点固支约束,另一端面通过参考点施加均匀的位移载荷;对邻近胶层的上下铺层间定义接触约束.为准确模拟每一铺层的损伤,对层合板逐层划分网格,并对搭接区域进行网格细化,胶层沿厚度方向划分一层网格,邻近胶层的两铺层间插入零厚度的内聚力单元以模拟分层损伤.图 4为有限元模型的细节,层合板采用减缩积分8结点连续壳单元(SC8R),胶层采用厚度为0.12 mm的三维内聚力单元(COH3D8),层间界面采用零厚度的三维内聚力单元.

图 4 单搭接接头有限元模型Fig. 4 Finite element models of single-lap joints
图选项
3 结果分析与讨论 3.1 失效模式与破坏形貌

图 5和图 6分别为搭接长度2.5 mm和20 mm接头的模拟结果.破坏形貌模拟与试验基本吻合,主要是胶层破坏和层合板铺层剥离,不同的破坏形貌反映接头发生了不同的失效模式.

图 5 搭接长度为2.5 mm的单搭接接头失效模式Fig. 5 Joints failure modes under 2.5 mm lap length
图选项

图 6 搭接长度为20 mm的单搭接接头失效模式Fig. 6 Joints failure modes under 20 mm lap length
图选项

当搭接长度为2.5 mm时,胶层的失效系数已经全部先后达到极限值,内聚力单元逐步删除,表示胶层发生了破坏(见图 5a);而层间界面和邻近胶层的基体大部分区域失效系数都很小,应力水平未满足损伤起始准则,无损伤发生(见图 5b和图 5c),故接头的失效模式主要为模式A.

当搭接长度为20 mm时,图 6a为模拟的破坏形貌,邻近胶层的铺层在搭接区域的部分被从下面板剥离开来黏附在胶层上,并从端部沿着纤维45°方向继续向外剥离撕裂,直至层合板的边缘,与试验现象相吻合;胶层只有端部小部分区域失效系数较大,大部分区域完好(如图 6b所示);而下面板在搭接区域内的层间界面完全失效,并从搭接区域端部沿着纤维45°方向向外扩展,直至层合板的边缘(如图 6c所示);被剥离铺层的基体的横向拉伸和剪切破坏因子的分布云图也反映了这一破坏过程,基体在搭接区域端部最先破坏,然后基体破坏沿纤维45°方向向外扩展(如图 6d所示),故接头的失效模式主要为模式B和C. 3.2 极限载荷

极限载荷的试验与模拟结果见图 7.可以看出,试验测定的极限载荷值的离散度均在10%以内,模拟结果与试验的相对误差均小于5%,吻合度较好,验证了有限元模拟的有效性.

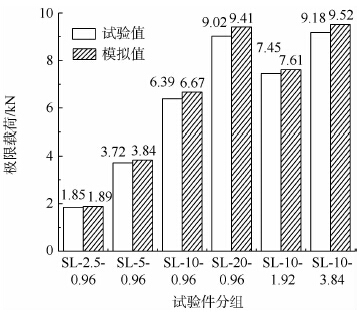图 7 试验与模拟的极限载荷值Fig. 7 Ultimate-loads of experiments and simulation
图选项

图 8为搭接长度20 mm的载荷-位移曲线,可以看出,模拟的最大载荷值比试验值略大,原因是试验件在工艺制备中可能存在胶层厚度不均匀、材料含有初始裂纹等固有缺陷,而且胶接区域越大,包含的固有缺陷越多,受其影响也越大,这在试验结果的离散度上也有所体现,胶接区域较大时,试验结果的离散度普遍较大.图 9为不同搭接长度下的极限载荷变化曲线,可以看出,极限载荷随搭接长度增大而增大,但增幅逐渐变缓,极限载荷趋于一稳定值.图 10为不同被胶接件厚度下的极限载荷变化曲线,可以看出,在本试验所测试的3种厚度(8层、16层、32层)下,极限载荷随被胶接件厚度增大基本呈线性增大.

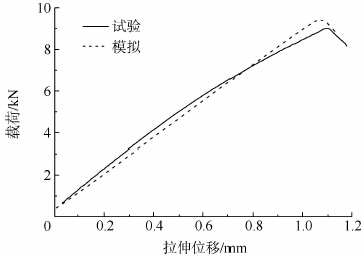图 8 试验与模拟的载荷-位移曲线Fig. 8 Load-displacement curves of experiments and simulation
图选项

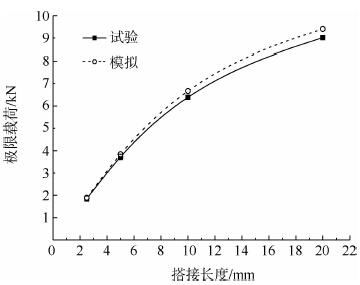图 9 不同搭接长度的极限载荷变化曲线Fig. 9 Ultimate-loads changing curves under different lap length
图选项

图 10 不同胶接件厚度的极限载荷变化曲线Fig. 10 Ultimate-loads changing curves under different adherend thickness
图选项
3.3 应力分析

选取搭接长度为20 mm的接头进行应力分析,根据加载历程中的载荷-位移曲线选取5个具有代表性的加载点(u=0.1,0.4,0.8,1.0,1.05 mm),相应的胶接区内的胶层应力和层间应力分布如图 11和图 12所示.

图 11 不同加载时刻胶层的应力分布Fig. 11 Stresses distribution of adhesive at different loading points
图选项

图 12 不同加载时刻邻近胶层铺层层间的应力分布Fig. 12 Interlaminar stresses distribution of plies adjacent to adhesive at different loading points
图选项

总体来看,由于胶层位于接头上下面板的中间对称位置,两端附加弯矩相等,故应力曲线呈对称分布;而由于载荷中心线偏离层间界面两端的距离不等,导致所受附加弯矩不相等,故应力曲线呈非对称分布.

图 11a和图 12a分别描述了胶层和层间的正应力σ33.可以看出,胶层正应力在胶接区中间的大部分区域应力水平较低,且处于负应力受压状态,而在靠近两端位置胶层正应力迅速增加,且高于同时刻的层间正应力;层间正应力在胶接区中间的大部分区域基本保持在零应力状态,而在靠近两端位置应力值迅速增长,右端的正应力水平高于左端,原因在于层间界面右端所受附加弯矩大于左端,而且左端的应力峰值随加载历程逐渐右移,说明层间界面的内聚力单元在混合模式下从左端向右逐渐发生失效.

图 11b和图 12b分别描述了胶层和层间的剪应力τ13,可以看出,胶层剪应力的分布呈两端高中间低的“凹”形分布,而层间剪应力的分布则呈一向右倾斜的“凹”形,左端高于右端;胶层和层间界面各位置处的应力值均随加载历程有较大增长,且在加载到一定程度后,曲线在两端处均有所下降,应力峰值开始从两端向内移动.

图 11c和图 12c分别描述了胶层和层间的剪应力τ23,可以看出,胶层剪应力呈中心对称,两端受力方向相反,而层间剪应力的右端值要高于左端和中间区域;但胶层和层间的剪应力τ23相比于σ33和τ13均较低,对接头失效影响也较小.

4 结 论

本文的研究为飞行器复合材料胶接结构设计提供了重要的试验和有限元分析方法,针对胶层厚度均为0.12 mm的T300/QY8911复合材料层合板单搭接胶接接头,通过对其在不同试验参数下的试验研究与数值模拟,得到如下结论:

1) 胶接连接的失效模式与胶接长度和被胶接件厚度有关,随胶接长度和被胶接件厚度的增加逐渐由胶层失效转变为层合板失效.

2) 接头强度随搭接长度和胶接件厚度增大而增大,但增幅逐渐变缓,最后趋于一稳定值.

3) 接头端部的应力集中和剥离应力最为严重,是失效的起始位置.

参考文献
[1] Volkersen O.Die nietkraftverteilung in zugbeanspruchten Nietv- erbindungen mit konstanten Laschenquerschnitten[J].Luftfahrtforschung,1938,15(1/2):41-47
[2] Goland M,Reissner E.The stresses in cemented joints[J].Journal of Applied Mechanics,1944,11(1):A17-A27
[3] Hart-Smith L J.Adhesive-bonded single-lap joints[M].Hampton,VA:Langley Research Center,1973
[4] Adams R D,Peppiatt N A.Stress analysis of adhesive-bonded lap joints[J].The Journal of Strain Analysis for Engineering Design,1974,9(3):185-196
Click to display the text
[5] Renton W J,Vinson J R.The efficient design of adhesive bonded joints[J].The Journal of Adhesion,1975,7(3):175-193
Click to display the text
[6] Allman D J.A theory for elastic stresses in adhesive bonded lap joints[J].The Quarterly Journal of Mechanics and Applied Mathematics,1977,30(4):415-436
Click to display the text
[7] Ribeiro F L,Borges L,Dalmeida J R M.Numerical stress analysis of carbon-fibre-reinforced epoxy composite single-lap joints[J].International Journal of Adhesion and Adhesives,2011,31(5):331-337
Click to display the text
[8] Da Costa Mattos H S,Sampaio E M,Monteiro A H.Static failure analysis of adhesive single lap joints[J].International Journal of Adhesion and Adhesives,2011,31(6):446-454
Click to display the text
[9] Hua Y,Gu L,Trogdon M.Three-dimensional modeling of carbon/epoxy to titanium single-lap joints with variable adhesive recess length[J].International Journal of Adhesion and Adhesives,2012,38:25-30
Click to display the text
[10] Ekh J,Schön J,Zenkert D.Simple and efficient prediction of bearing failure in single shear,composite lap joints[J].Composite Structures,2013,105:35-44
Click to display the text
[11] Tang J H,Sridhar I,Srikanth N.Static and fatigue failure analysis of adhesively bonded thick composite single lap joints[J].Composites Science and Technology,2013,86:18-25
Click to display the text
[12] Groth H L,Brottare I.Evaluation of singular intensity factors in elastic-plastic materials[J].Journal of Testing and Evaluation,1988,16(3):291-297
Click to display the text
[13] Wahab M M A,Ashcroft I A,Crocombe A D,et al.Prediction of fatigue thresholds in adhesively bonded joints using damage mechanics and fracture mechanics[J].Journal of Adhesion Science and Technology,2001,15(7):763-781
Click to display the text
[14] De Moura M F S F,Gonçalves J P M,Chousal J A G,et al.Cohesive and continuum mixed-mode damage models applied to the simulation of the mechanical behaviour of bonded joints[J].International Journal of Adhesion and Adhesives,2008,28(8):419-426
Click to display the text
[15] Anyfantis K N,Tsouvalis N G.A 3D ductile constitutive mixed-mode model of cohesive elements for the finite element analysis of adhesive joints[J].Journal of Adhesion Science and Technology,2013,27(10):1146-1178
Click to display the text
http://dx.doi.org/10.13700/j.bh.1001-5965.2014.0010
北京航空航天大学主办。
0

文章信息

梁祖典, 燕瑛, 张涛涛, 李剑峰, 孟祥吉, 廖宝华
Liang Zudian, Yan Ying, Zhang Taotao, Li Jianfeng, Meng Xiangji, Liao Baohua
复合材料单搭接胶接接头试验研究与数值模拟
Experimental investigation and numerical simulation of composite laminate adhesively bonded single-lap joints
北京航空航天大学学报, 2014, 40(12): 1786-1792
Journal of Beijing University of Aeronautics and Astronsutics, 2014, 40(12): 1786-1792.
http://dx.doi.org/10.13700/j.bh.1001-5965.2014.0010

文章历史

收稿日期：2014-01-13
网络出版日期: 2014-06-09

相关文章

工作空间