表1(Table 1)
2. 中国人民解放军信息工程大学 导航与空天目标工程学院, 郑州 450052;
3. 西安测绘研究所 地理信息工程国家重点实验室, 西安 710054
2. Institute of Navigation & Aerospace Targets Engineering, PLA Information Engineering University, Zhengzhou 450052, China;
3. National Key Laboratory of Geo-information Engineering, Xi'an Institute of Surveying and Mapping, Xi'an 710054, China
编队卫星飞行是国内外航天界普遍关注的一个研究领域,实时相对定轨可以为编队飞行控制提供实时相对位置和实时相对速度信息,是完成编队卫星飞行任务的重要技术途径[1, 2, 3, 4, 5, 6].目前,基于GPS(Global Positioning System)的编队卫星实时相对定轨已经在德国TanDEM-X(TerraSAR-X add-on for Digital Elevation Measurement)等编队飞行任务中得到实现.在基于GPS的编队卫星实时相对定轨中,单频GPS接收机具有重要作用,如德国TanDEM-X除了搭载双频GPS接收机进行高精度事后测量外,还搭载了单频接收机进行实时相对定轨和时间同步[7, 8, 9],瑞典的PRISMA(Prototype Research Instruments and Space Mission technology Advancement)同样搭载了单频接收机用于实时相对定轨[9].因此,开展基于单频GPS接收机的编队卫星实时相对定轨具有重要意义.
基于GPS的编队卫星实时相对定轨依据采用的动力学信息情况,可以分为几何法和动力法[9, 10, 11, 12],其中几何法不采用动力学信息,相对定位精度受GPS几何结构影响较大,且不能保证结果的连续性,而动力法需要采用动力学信息,它能够提供连续的相对位置信息,精度也较几何法高,在实时相对定轨中动力法多采用滤波算法,为平衡观测信息和动力学信息,我国学者杨元喜在动态自适应滤波的基础上提出了单颗卫星的自适应定轨算法[13, 14, 15, 16].
地面的动态自适应定位及单颗卫星的自适应定轨算法可以参考文献[13, 14, 15, 16],本文给出编队卫星的自适应滤波相对定轨算法,为验证算法可行性及精度,同时考虑到单频GPS接收机在实时相对定轨中的普遍性,文章采用两颗GRACE(Gravity Recovery and Climate Experiment)卫星的星载GPS单频伪距观测数据进行了试验计算,并利用JPL(Jet Propulsion Laboratory)轨道对相对定轨结果进行了外部检验. 1 自适应滤波相对定轨 1.1 自适应滤波相对定轨原理
编队卫星自适应滤波相对定轨算法可以采用时间更新和测量更新两个过程进行描述.
时间更新过程的目的是计算两颗编队卫星的状态预报值xk及其协方差矩阵Pk:
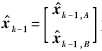为tk－1时刻两颗编队卫星的状态估值;
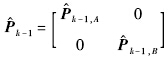为tk－1时刻两颗编队卫星的状态协方差矩阵;
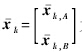为tk时刻两颗编队卫星的状态预报值;αk为tk时刻自适应因子;
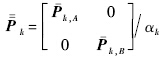为tk时刻两颗编队卫星的状态预报等价协方差矩阵;Φk=Φ
为tk－1到tk时刻两颗编队卫星的状态转移矩阵;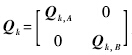
时刻两颗编队卫星的系统状态噪声矩阵,下标A,B分别代表两颗编队卫星A和卫星B.
测量更新过程的目的是计算增益矩阵及编队卫星的状态估值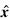
k及其协方差矩阵
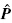k:
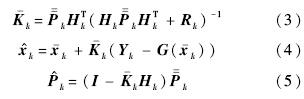
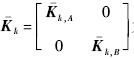为tk时刻滤波增益矩阵;
为tk时刻两颗编队卫星的观测矩阵;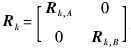
为tk时刻两颗编队卫星的观测噪声方差矩阵;
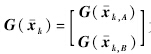为tk时刻两颗编队卫星的测量理论值;Yk=
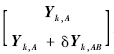为tk时刻两颗编队卫星的观测向量,Yk,A为卫星A的观测向量(即卫星A的伪距单点定位结果),δYk,AB为两颗卫星的观测向量差(即差分GPS计算的伪距相对定位结果).
1.2 自适应因子
由自适应滤波相对定轨原理可以看出,自适应滤波相对定轨通过自适应因子αk调整编队卫星的状态预报协方差矩阵.
为避免αk=0,本文αk取为
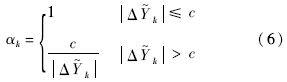
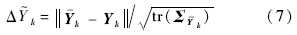
在自适应滤波相对定轨中,如果采用参考星A的位置预报值Yk,A及观测值Yk,A计算自适应因子αk,则自适应滤波相对定轨步骤可以简化为:
1) 采用伪距单点定位计算参考星A几何位置;
2) 采用伪距差分方法计算辅星B几何位置;
3) 以A星几何位置为观测值进行定轨,并计算自适应因子;
4) 固定A星自适应因子,以B星几何位置为观测值进行定轨.
如果令αk=1,则自适应滤波相对定轨退化为卡尔曼滤波相对定轨.
由卡尔曼滤波相对定轨和自适应滤波相对定轨的计算步骤可以得知,在自适应滤波相对定轨中,参考星A通过单颗卫星的自适应定轨获得轨道信息,辅星B通过采用参考星A的自适应因子调整观测信息和相对动力学信息.在卡尔曼滤波相对定轨中,参考星A通过单颗卫星的卡尔曼滤波定轨获得轨道信息,辅星B通过以差分定位结果为观测值的卡尔曼滤波定轨获得轨道信息.比较两种相对定轨原理及步骤可以发现,自适应滤波相对定轨可以通过自适应因子调整观测信息和相对动力学信息. 2 计算分析 2.1 计算方案
文章采用两颗GRACE卫星2005-12-09—10的星载GPS观测数据,进行了实时相对定轨试验
计算.两颗GRACE卫星在2005年12月进行了变轨,期间两颗卫星的星间距离变化为431m到37km,其基线长如图 1所示.
 |
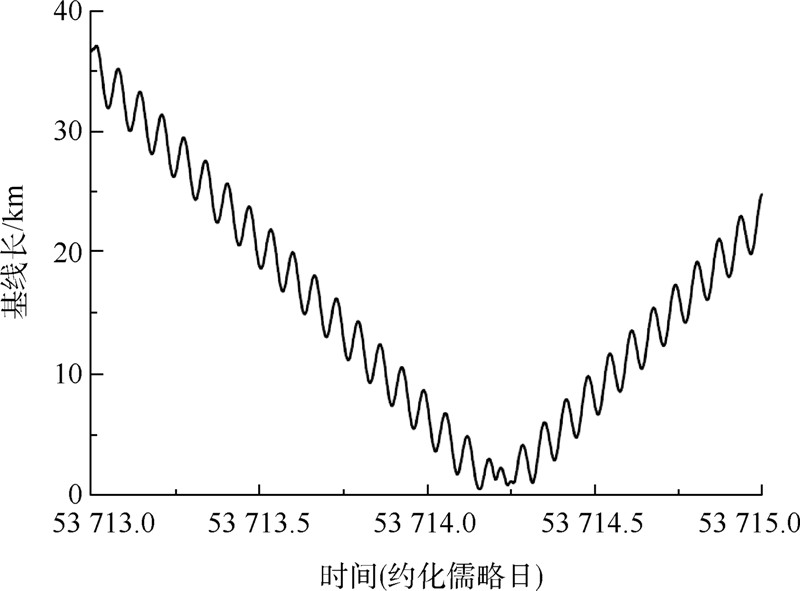| 图 1 两颗GRACE卫星间的基线长Fig. 1 Baseline of two GRACE satellites |
相对定轨试验采用3种方案:
1) 几何法(伪距差分相对定位结果);
2) 卡尔曼滤波相对定轨;
3) 自适应滤波相对定轨.
计算时采用的数据为GRACE-A/B两颗卫星的C/A码观测数据(采样间隔10s)和广播星历,卡尔曼滤波相对定轨和自适应滤波相对定轨采用的力学模型仅考虑重力场(30×30阶次),积分器采用4阶Runge-Kutta积分器,积分步长为10s.位置和速度的初始方差分别为100.0m2和1.0m2/s2,位置和速度的状态噪声分别为10-6m2和10-12m2/s2,观测噪声为100.0m2. 2.2 结果分析
为验证自适应滤波相对定轨的可行性和有效性,文章采用JPL轨道检核了3种方案的试验结果,JPL轨道的3维位置精度约为3cm.
表 1给出了3种方案的相对位置结果统计值.
| 相对定轨方法 | x/m | y/m | z/m | 基线 | ||||
| 平均值 | 标准差 | 平均值 | 标准差 | 平均值 | 标准差 | 平均值 | 标准差 | |
| 几何法 | 0.088 | 1.932 | -0.11/0 | 2.520 | 0.135 | 1.296 | -0.070 | 1.482 |
| 卡尔曼滤波 | -0.002 | 0.075 | -0.001 | 0.108 | -0.055 | 0.101 | -0.063 | 0.119 |
| 自适应滤波 | -0.001 | 0.068 | 0.005 | 0.070 | -0.001 | 0.068 | -0.015 | 0.057 |
从表 1可以看出:卡尔曼滤波相对定轨和自适应滤波相对定轨精度明显高于几何法的相对定轨精度,3种方案中自适应滤波相对定轨精度最高,其结果与JPL轨道差值在3个方向上可以达到7cm的精度,基线精度可以达到6cm,且不存在明显的系统差.
图 2给出了卡尔曼滤波相对定轨和自适应滤波相对定轨的基线残差图.图 3给出了自适应因子的变化情况.
从图 2可以看出：卡尔曼滤波相对定轨和自适应滤波相对定轨都能快速收敛,但自适应滤波相对定轨比卡尔曼滤波相对定轨具有较强的稳定性.
 |
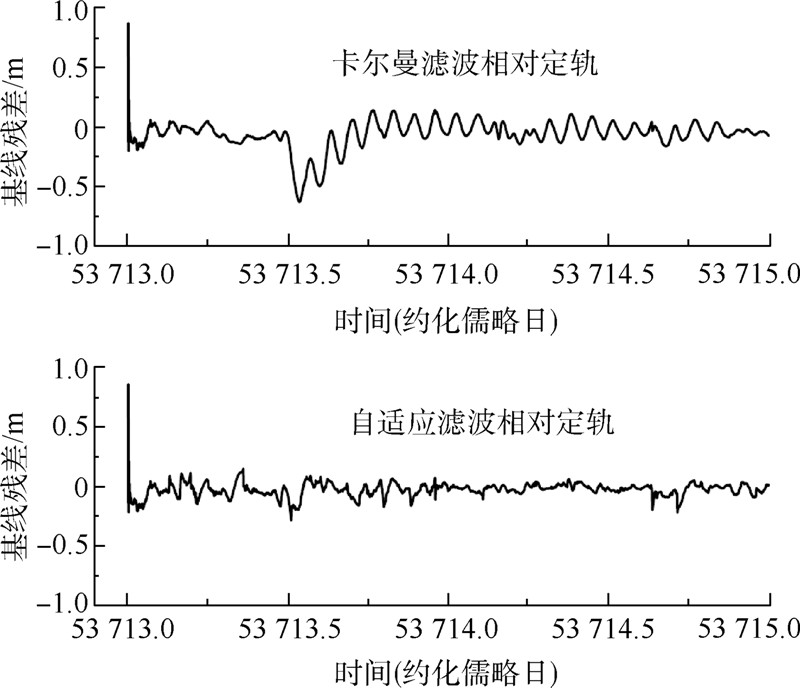| 图 2 相对定轨基线与JPL轨道基线比较残差图Fig. 2 Residuals of baseline comparison between relative orbits and JPL orbits |
比较图 1、图 2可以看出:卡尔曼滤波相对定轨和自适应滤波相对定轨得到的星间基线精度与星间基线长度相关,特别是自适应滤波相对定轨计算的星间基线精度明显随着基线长度的减小而提高.
由图 2、图 3可以看出:在自适应滤波相对定轨中,由于辅星B通过采用参考星A的自适应因子,可以调整观测信息和两颗卫星间的相对动力学信息权比,所以,自适应滤波相对定轨的基线残差明显小于卡尔曼滤波相对定轨的基线残差.
 |
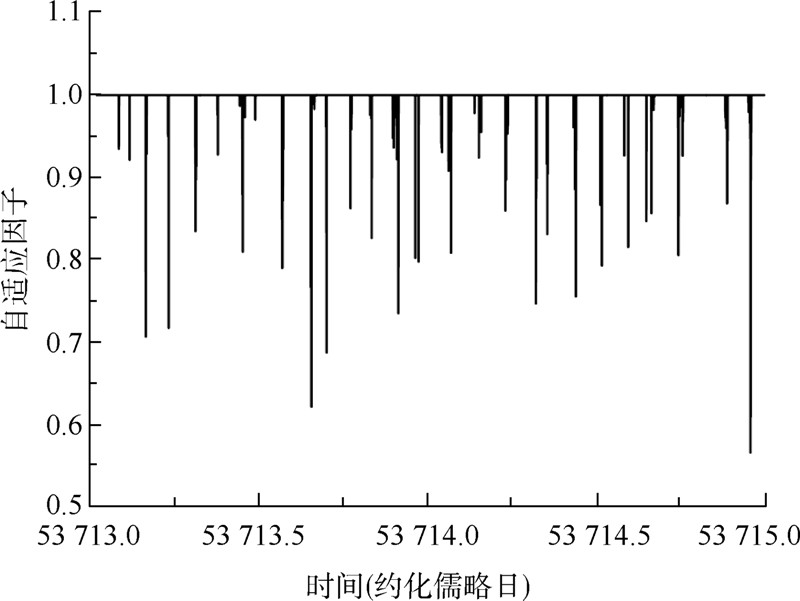| 图 3 自适应因子变化图Fig. 3 Variation of adaptive factor |
由表 1、图 2和图 3可以看出:自适应因子的调节,使得自适应滤波相对定轨能够较好地平衡编队卫星间的观测信息和相对动力学信息,进而得到高精度的相对定轨结果. 3 结 论
通过以上的计算分析,可以得出以下结论:
1) 与卡尔曼滤波相对定轨相比,自适应滤波相对定轨通过自适应因子调节,可以较好地平衡编队卫星间的观测信息和相对动力学信息,得到高精度的相对定轨结果,且稳定性较强.
2) 采用自适应滤波相对定轨计算的星间基线精度随着基线长度的减小而提高,且收敛速度快.
3) GRACE卫星实测数据计算表明,采用单频伪距和广播星历进行自适应滤波相对定轨,可以得到精度优于6cm的星间基线.
| [1] | Remco K.Precise relative positioning of formation flying spacecraft using GPS[D].Delft:Nederlandse Commissie voor Geodesie Netherlands Geodetic Commission,2006 |
| [2] | 马骏,肖业伦.编队星座相对位置精确测定与自主定轨方法[J].北京航空航天大学学报,2008,34(6):665-668 Ma Jun,Xiao Yelun.Autonomous orbit determination and precise measurement of relative position of formation constellation [J].Journal of Beijing University of Aeronautics and Astronautics,2008,34(6):665-668(in Chinese) |
| Cited By in Cnki (6) | Click to display the text | |
| [3] | 王威.GPS用于对地观测编队卫星状态的高精度确定[D].郑州:信息工程大学,2004 Wang Wei.Precise state determination of formation satellite for earth observation using GPS[D].Zhengzhou:Information Engineering University,2004(in Chinese) |
| Cited By in Cnki (5) | |
| [4] | 王海涛,欧吉坤,袁运斌.两步法快速解算编队卫星GPS模糊度[J].北京航空航天大学学报,2009,35(9):1130-1133 Wang Haitao,Ou Jikun,Yuan Yunbin.Rapid resolution of GPS ambiguities of satellite formation flying with two-step method[J].Journal of Beijing University of Aeronautics and Astronautics,2009,35(9):1130-1133(in Chinese) |
| Cited By in Cnki (1) | Click to display the text | |
| [5] | 苏建敏,董云峰.利用人工势函数法的卫星电磁编队控制[J].北京航空航天大学学报,2012,38(2):213-217 Su Jianmin,Dong Yunfeng.Artificial potential function method for satellite electromagnetic formation control[J].Journal of Beijing University of Aeronautics and Astronautics,2012,38(2):213-217(in Chinese) |
| Cited By in Cnki (2) | Click to display the text | |
| [6] | 孙文超,常青,徐勇,等.星间DOWRT中的相对论效应分析与修正[J].北京航空航天大学学报,2012,38(3):335-339 Sun Wenchao,Chang Qing,Xu Yong,et al.Analysis and correction on relativistic effect of inter-satellites using dual one-way ranging/time synchronization[J].Journal of Beijing University of Aeronautics and Astronautics,2012,38(3):335-339(in Chinese) |
| Cited By in Cnki (2) | Click to display the text | |
| [7] | Montenbruck O,Kahle R,D’Amico S, et al.Navigation and control of the TanDEM-X formation[J].Journal of the Astronautical Sciences,2008,56(3):341-357 |
| Click to display the text | |
| [8] | Montenbruck O,Wermuth M,Kahle R.GPS based relative navigation for the TanDEM-X mission-first flight results[J].Journal of the Institute of Navigation,2011,58(4):293-304 |
| Click to display the text | |
| [9] | D’Amico S,Montenbruck O.Differential GPS:an enabling technology for formation flying satellites[R].IAA-B7-1403,2009 |
| [10] | Kawano I,Mokuno M,Kasai M,et al.First autonomous rendezvous using relative GPS navigationby ETS-VII[C]//Proceedings of the 12th International Technical Meeting of the Satellite Division of the Institute of Navigation.Nashville,Tennesee:ION,1999:393-400 |
| [11] | 刘洋,徐毓.无轨道动力学模型的增强型GPS实时星间相对定位方法[J].空间科学学报,2011,31(2):246-253 Liu Yang,Xu Yu.Inter-satellite real-time relative positioning method based on augmented GPS without orbit dynamic model[J].Chinese Journal Space of Science,2011,31(2):246-253(in Chinese) |
| Cited By in Cnki | |
| [12] | Wu S C,Bar-Sever Y.Real-time sub-cm differential orbit determination of two low-earth orbiters with GPS bias fixing[C]//Proceedings of the 19th International Technical Meeting of the Satellite Division of the Institute of Navigation.Fort Worth,Texas:ION,2006:2515-2522 |
| [13] | Yang Y,He H,Xu G.Adaptively robust filtering for kinematic geodetic positioning[J].Journal of Geodesy,2001,75(2/3):109-116 |
| Click to display the text | |
| [14] | Yang Y,Wen Y.Synthetically adaptive robust filtering for satellite orbit determination[J].Science in China,Series D,2004,47(7):585-592 |
| Click to display the text | |
| [15] | 杨元喜,文援兰.卫星精密轨道综合自适应抗差滤波技术[J].中国科学(D辑),2003,32(11):1112-1119 Yang Yuanxi,Wen Yuanlan.Synthetically adaptive robust filtering for satellite orbit determination[J].Science in China,Series D,2003,32(11):1112-1119(in Chinese) |
| Cited By in Cnki (47) | Click to display the text | |
| [16] | 杨元喜,秦显平.自适应定轨与约化动力定轨理论分析与比较[J].测绘科学与工程,2013,33(1):1-4 Yang Yuanxi,Qin Xianping.Theoretical analysis and comparison between adaptive and reduced dynamic orbit determination[J].Geomatics Science and Engineering,2013,33(1):1-4(in Chinese) |
| Cited By in Cnki |
