2. 北京航空航天大学 先进航空发动机协同创新中心, 北京 100191
2. Collaborative Innovation Center of Advanced Aero-Engine, Beijing University of Aeronautics and Astronautics, Beijing 100191, China
随着先进传感技术和人工智能技术的迅速发展,飞行器等复杂系统健康管理技术逐渐成为国内外科研院所和军工部门研究者关注的焦点.飞行器健康管理系统(AHMS,Aircraft Health Management System)是指基于先进传感器网络布局,设计各种智能算法与推理模型来监测、诊断、预测与管理飞行器健康状态的一种自主式后勤保障系统.AHMS设计完成之后,其性能是否达到规定的要求,需要通过验证与评估来确认.此外,通过验证与评估所得到的反馈信息还可以对AHMS的设计进行改进和完善.验证与评估是AHMS设计与应用的关键环节[1].
目前,AHMS研究领域已经出现了许多用于评估故障预测算法的性能指标[2, 3, 4].根据性能指标所能提供的有用信息与功能,通常将这些指标分为3类:①技术性能指标,可以被进一步划分为准确度指标、鲁棒性指标、精密度指标和策略性指标,这类指标通过比较预测值与理想值之间的误差来评估算法性能;②计算性能指标,这类指标量化算法的复杂度、CPU占用率、内存占用率等;③费效指标,这类指标测量预测收益,与剩余使用寿命(RUL,Remaining Useful Life)预测准确度密切相关,RUL预测准确度高,则收益高.以上这些指标为定性或定量分析故障预测算法的性能提供了客观的依据.
但是,运用这些性能指标都要满足一个重要前提条件,即在评估故障预测算法性能时需要预先获得对象系统RUL的理想值,通过比较RUL的预测值与理想值来计算故障预测算法的性能,它们仅能用于系统失效后而不是在运行过程中,因为只有当系统失效后,才可以得到对象系统RUL的理想值.对于飞行器等复杂系统来说,这将是一个漫长的过程.同时,由于故障预测算法的基本思想是通过估计某个或某些特定参数的状态演变来预测对象系统或部件的故障状态或RUL值,预测过程本身受到测量、环境、负载等诸多不确定因素的影响而具有很大的不确定性,但是,在运用这些指标评估故障预测算法性能时却未能将这些不确定因素考虑进去[5, 6].
由于衡量故障预测算法的输出结果是否稳定是评估该算法是否优良的重要依据[2, 7],因此,为了解决上述问题,本文提出了一种不依赖于对象系统RUL理想值,且能从稳定性角度实时评估故障预测算法性能的评估方法. 1 系统健康退化过程
依据本文作者在文献[8]中所作研究可知:对于不可修复系统(或可修复系统不采取修复操作),其健康退化过程曲线如图 1所示.
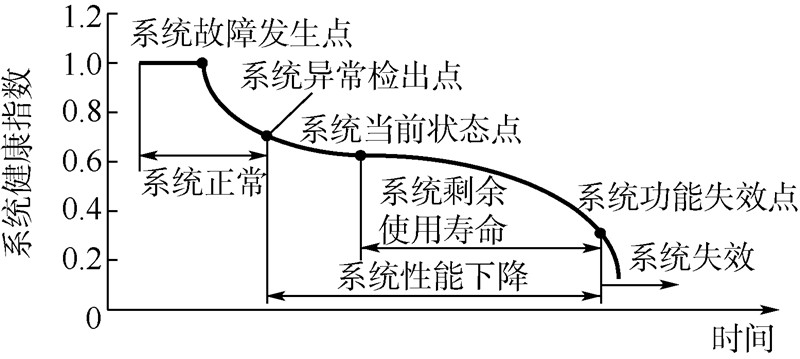 |
| 图 1 系统健康退化过程曲线Fig. 1 System health degradation curve |
由图 1可知,在“系统异常检出点”和“系统功能失效点”之间,由于系统故障程度逐渐增强,这段时间系统处于性能下降状态,直至系统功能完全失效.故障预测的主要任务就是在检测出系统异常之后,根据系统当前状态和使用负载情况预测出系统的功能失效发生时间,即预测出系统的剩余使用寿命,如图 1所示,从“系统当前状态点”到“系统功能失效点”的这段时间称为“系统的RUL”. 2 稳定性实时评估方法 2.1 对象系统虚构寿命
假设某种故障预测算法在“系统异常检出点”后开始启动,在n个时间点对对象系统的RUL进行了预测(n个时间点的选取可以是随机的),如果假设tP代表第1个预测时间点,i代表第i个预测时间点,tEoP代表第n个预测时间点,那么在故障预测算法启动后直至对象系统完全失效,记完全失效时间点为tEoL,则总共获得了n个RUL预测值(prognostic value),记为{LPi|i=1,2,…,n},其中LPi表示在第i个时间点进行预测所获得的RUL预测值.
对应LPi,可以统计出对象系统在第i个时间点相应的已消耗寿命的数值(consumed value),记为LCi,同时,假设此时间点RUL的理想值(ideal value)可表示为LIi.于是,可知对象系统在第i个时间点的理想寿命(ideal life),记为ILi,其表达式为
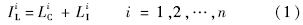
为了便于研究,区别于对象系统理想寿命,在文献[9]基础上计算对象系统“虚构寿命”(fictitious life).将对象系统在第i个时间点的虚构寿命值记为FLi,并且假设:
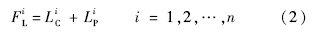
在n个预测时间点可以得到n个对象系统的虚构寿命值,记为{FLi|i=1,2,…,n}.对象系统虚构寿命示意图如图 2所示.
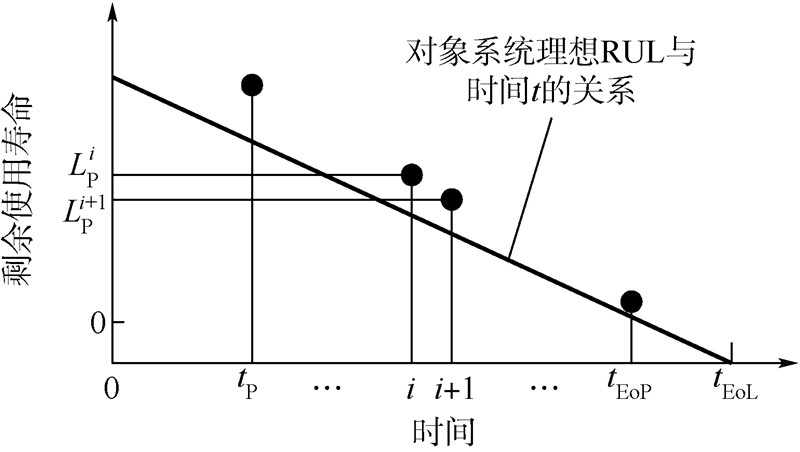 |
| 图 2 对象系统虚构寿命示意图Fig. 2 Schematic diagram for the fictitious life |
图 2所示二维坐标系中,横轴为时间轴,纵轴为剩余使用寿命预测值轴,斜线段表示对象系统理想RUL与时间t的关系,4个黑色圆点为假设的某种故障预测算法在对应时间点所获得的RUL预测值.
由对应关系可知,第i个预测时间点的RUL预测值为LPi,而此时的对象系统已消耗寿命数值为LCi,由式(2)可得此时对象系统虚构寿命值.
同理,可得对象系统在第i+1个时间点的虚构寿命值为
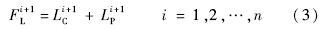
通过上面的分析可知,当对象系统的n个预测时间点选定之后,在每个预测时间点的RUL预测值LPi和已消耗寿命数值LCi均可实时地获得,从而由式(2)可以实时地求出每个预测时间点的虚构寿命值FLi.由于测量数据都是实时获取的,从而克服了以往性能评估方法未能将操作、环境与负载等不确定因素对测量数据的影响考虑进去的弊端.当每个预测时间点的虚构寿命值与其理想寿命值越接近时,则说明了该故障预测算法的预测结果越准确,同时,也说明了该算法本身具有很好的预测稳定性.
参考统计学方法设计本文的实时评估算法.首先,计算{FLi|i=1,2,…,n}的平均值,记为E(FL),则有

由于方差或均方差都是用于衡量一组数据波动大小的统计量,其值越大,样本数据的波动性就越大,对应的该组数据的稳定性就越小.于是,计算虚构寿命值{FLi|i=1,2,…,n}的均方差,记为σ(FL),则有
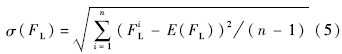
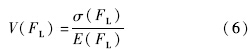
由式(6)计算出来的V(FL)值越小,说明该组虚构寿命值的波动越小,其对应的故障预测算法的稳定性越好.
于是,针对同一对象系统,通过比较V(FL)的大小,可以在对象系统理想RUL值未知情况下,实时地评估两种或多种故障预测算法的稳定性,为用户选取适宜于特定对象系统的故障预测算法提供客观依据. 其评估流程如图 3所示.
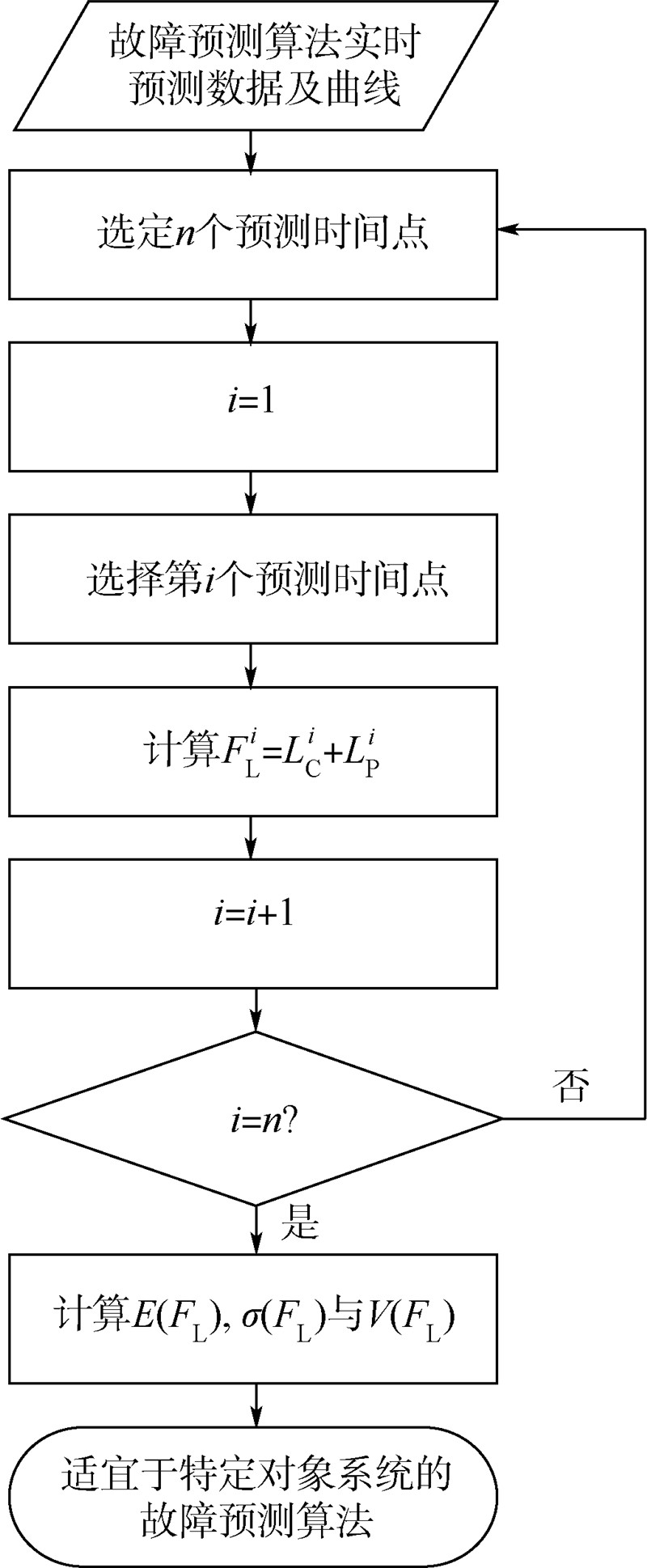 |
| 图 3 评估流程图Fig. 3 Evalution flow chart |
如图 3所示,具体评估流程步骤为:
1) 实时地获取故障预测算法关于某对象系统的RUL预测数据并绘制相应曲线;
2) 对应曲线在时间轴上选定n个预测时间点;
3) 根据式(2)依次计算n个预测时间点对应的虚构寿命{FLi|i=1,2,…,n}数值;
4) 根据式(4)~式(6)依次计算n个预测时间点的E(FL),σ(FL)与V(FL)的值,并根据虚构寿命变异系数V(FL)的大小判断故障预测算法的实时稳定性. 3 实验方案与结果分析 3.1 实验方案
本文针对机电作动器匝间绕组短路故障,利用模型仿真数据来验证前文中提出的故障预测算法稳定性实时评估方法的有效性.
1) 故障演化仿真数据的生成原理. 由Matlab电机模型生成故障演化情况的仿真数据[10].具体涉及到的机电作动器故障演化模型表达式为
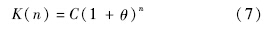
2) 故障缓变模型参数设置. 基于故障演化模型,设计故障缓变过程如下: 短路电阻报警阈值为200Ω; 失效阈值设置为80Ω; 模型参数C=200,θ=5.89×10-6. 计算可知,检出故障后,系统在43.2min左右达到失效阈值.
2) 故障预测算法选取. 鉴于基于粒子滤波[11](PF,Particle Filtering)和递归最小二乘[12](RLS,Recursive Least Squares)两种故障预测算法均具有较快的RUL预测值收敛速度,并可对对象系统的模型参数进行估计,本文选用这两种算法来验证实时评估方法的优越性与可行性.
为了得到较为精确的评估数据,将故障预测算法的数据更新间隔设置为每秒更新一次,每次都会输出算法对应的机电作动器RUL数值. 3.2 结果分析
分别依据文献[4]中提出的HP指标(Prognostic Horizon)和α-λ性能指标考核两种故障预测算法的性能;与利用本文提出的实时稳定性评估方法得出的结论相比较,以便验证本文所提方法的可行性.
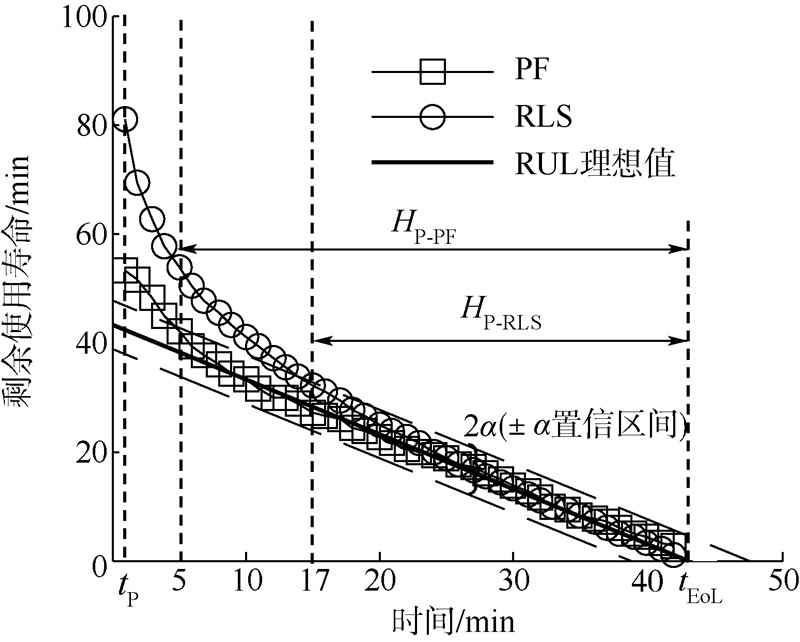
根据HP指标来评估PF和RLS两种算法的性能,HP指标的定义和计算方法详见文献[4],此处根据实际情况选取置信区间参数α=0.1,评估结果如图 4所示.
 |
| 图 4 HP性能指标对比图Fig. 4 Comparison chart of HP metric |
从图 4可知,PF算法和RLS算法的预测值分别在5min和15min时第1次进入±α置信区间,且直至tEoP(表示预测算法结束预测行为的时间点),两种算法的预测值均落在了±α置信区间内.根据HP指标的定义方法,将两种算法的HP指标值分别标示在图 4中,PF和RLS算法的HP指标值分别标示为HP-PF和HP-RLS,显然,前者大于后者,初步说明了PF算法比RLS算法更适宜于预测该对象系统的RUL.
采用更严格的α-λ性能指标来评估两种算法的性能,此处α是一个与具体预测时间点i相关的时间函数,可表达成α=α(i),假设α的初始值α=0.1,i∈(tP,tEoP),i等价于α-λ性能指标中的λ参数.如图 4所示,HP指标中的±α置信区间为梯形范围,而在图 5中,α-λ性能指标中的该置信区间为一个三角形区域,该指标判断在某一预测时间点相应算法的预测值是否落在了该区域内.相应地,可知PF算法的预测值更快更紧密地落在了该三角形区域,说明了运用于机电作动器匝间短路故障及其RUL值的预测时,PF算法更优.
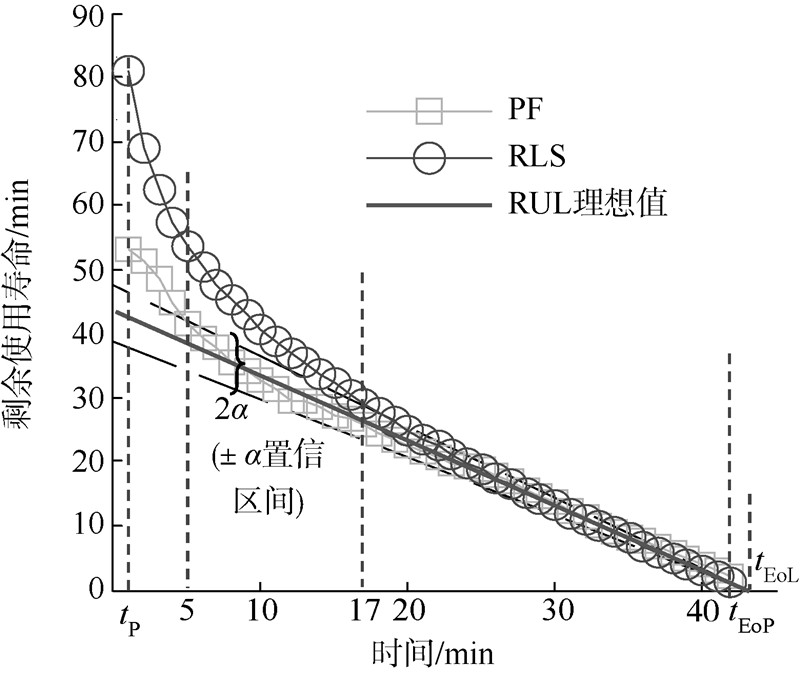 |
| 图 5 α-λ性能指标对比图Fig. 5 Comparison chart of α-λ metric |
采用本文提出的实时评估方法从稳定性角度来实时比较两种故障预测算法的性能.按照评估流程步骤,实时地获取两种故障预测算法对于机电作动器匝间短路故障的RUL预测数据并绘制相应曲线,如图 6所示.
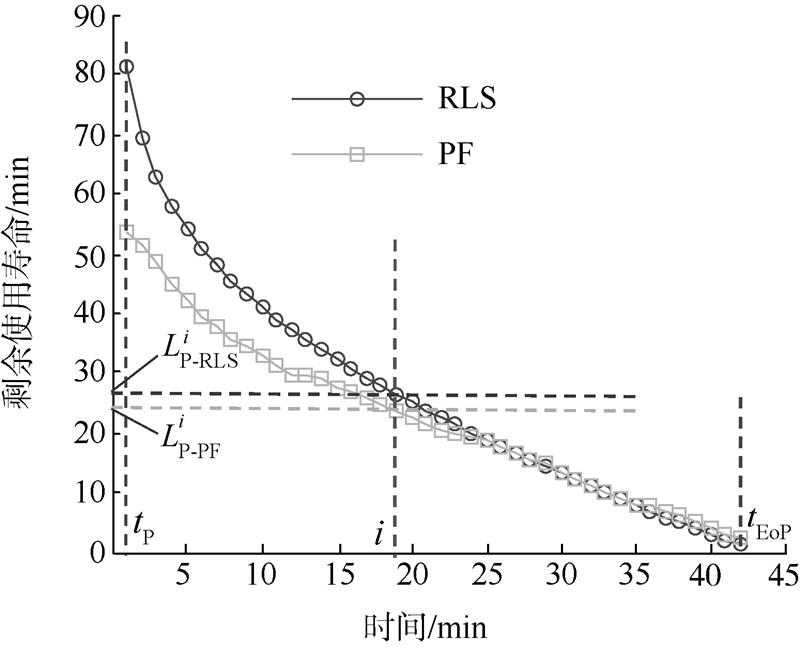 |
| 图 6 实时稳定性指标对比图Fig. 6 Comparison chart of stability metric |
本例中对应RLS和PF两种预测算法的RUL预测曲线选取n=42个预测时间点,其中,令tP为第1个预测时间点,tEoP为第42个预测时间点,i表示第i个预测时间点,如图 6中所示,对应第i个预测时间点,RLS算法和PF算法的RUL预测值分别为LP-RLSi和LP-PFi,由此,根据式(2)分别计算RLS和PF算法在选定的n=42个预测时间点的虚构寿命数值{FLi|i=1,2,…,42}同时,根据式(4)~式(6)分别计算两种预测算法的E(FL),σ(FL)与V(FL)数值,其计算结果如表 1所示.
| 故障预测算法 | E(FL) | σ(FL) | V(FL) |
| RLS | 48.34 | 8.52 | 0.18 |
| PF | 44.16 | 2.79 | 0.06 |
如表 1所示,RLS算法的均方差为8.52,而PF算法的均方差为2.79,后者小于前者,可知PF算法所获得的n个虚构寿命值较多地集中于均值附近,即PF算法稳定性更好.为了消除由于均值不同带来的影响,进一步计算两者的虚构寿命变异系数,由于0.18>0.06,即PF算法的虚构寿命变异系数远小于RLS算法的,所以依据稳定性能的判定准则可知:针对机电作动器匝间短路故障及其RUL值的预测,PF算法的稳定性能更优,用户可以优先选择PF算法.这一结论与利用HP指标和α-λ性能指标在需要获知RUL理想值时获得的结论相同. 4 结 论
基于对第3节中仿真案例的分析,可以得出以下结论:①所提方法在不需要RUL理想值时得出的评估结论与运用文献[4]提出指标、在需要预先获知机电作动器匝间绕组RUL理想值前提下得出的评估结论保持一致. ②通过计算虚构寿命的变异系数可以间接评估对应的故障预测算法的稳定性,为用户的选择提供客观依据. ③由于剩余使用寿命预测值可以实时地获得,本方法可以克服以往评估方法未考虑不确定因素对测量数据影响的弊端,具有实时评估特性.
| [1] | 王志鹏,吕琛,王自力,等.飞机PHM演示验证平台设计技术研究[J].南京理工大学学报,2011,35(增刊):250-255 Wang Zhipeng,Lü Chen,Wang Zili,et al.Design of PHM demonstration and verification platform[J].Journal of Nanjing University of Science and Technology,2011,35(Supplement):250-255(in Chinese) |
| [2] | Abhinav S,Jose C,Bhaskar S.Evaluating algorithm performance metrics tailored for prognostics[C]//Aerospace Conference.Piscataway,NJ:IEEE,2008:1-13 |
| [3] | Abhinav S,Jose C,Bhaskar S,et al.On applying the prognostic performance metrics[C]//Prognostics and Health Management.New York:IEEE,2009:478-485 |
| [4] | Abhinav S,Jose C,Bhaskar S,et al.Metrics for offline evaluation of prognostic performance[J].International Journal of Prognostic and Health Management,2010,1(1):1-20 |
| Click to display the text | |
| [5] | Tang L,Kacprzynski G J,Goebel K,et al.Methodologies for uncertainty management in prognostics[C]//Aerospace conference,2009 IEEE.[S.l.]:IEEE,2009:1-12 |
| [6] | Gu J,Barker D,Pecht M.Uncertainty assessment of prognostics implementation of electronics under vibration loadings[J].Microelectronics Reliability,2007,47(12):1849-1856 |
| Click to display the text | |
| [7] | Roemer M J,Dzakowic J,Orsagh R F,et al.Validation and verification of prognostic and health management technologies[C]//Aerospace Conference,2005 IEEE.Atlanta:IEEE,2005:3941-3947 |
| [8] | 梁旭,李行善,张磊,等.支持视情维修的故障预测技术研究[J].测控技术,2007,26(6):5-8 Liang Xu,Li Xingshan,Zhang Lei,et al.Survey of fault prognostics supporting condition based maintenance[J].Measurement and Control Technology,2007,26(6):5-8(in Chinese) |
| Cited By in Cnki (71) | |
| [9] | Shi J Y,Shi M,Wang L,et al.Performance evaluation method of remaining useful life prediction based on pseudo life[C]//Industrial Engineering and Engineering Management.Piscataway,NJ:IEEE,2011:1118-1122 |
| [10] | 吴豪.机电作动器故障预测与健康管理关键技术研究[D].北京:北京航空航天大学,2012 Wu Hao.Key technologies of fault prognosis and health management for electro-mechanical actuator[D].Beijing:Beijing University of Aeronautics and Astronautics,2012(in Chinese) |
| [11] | Arulampalam M S,Maskell S,Gordon N,et al.A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking[J].IEEE Transactions on Signal Processing,2002,50(2):174-188 |
| Click to display the text | |
| [12] | Simon D.Optimal state estimations[M].Hoboken,New Jersey:John Wiley and Sons,2006 |


