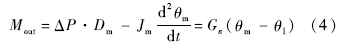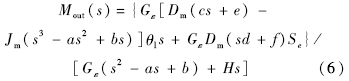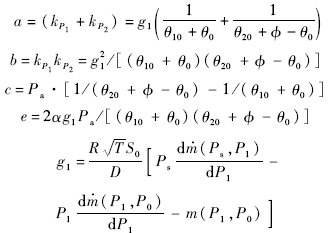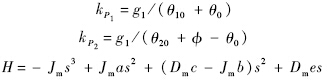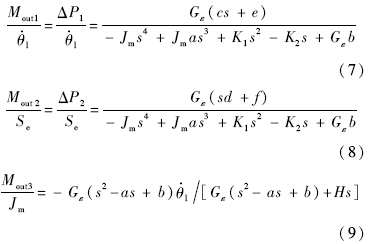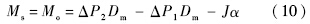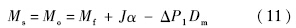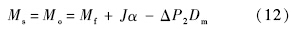负载模拟器通过主动控制执行元件实现对被测对象进行加载,广泛应用于飞行器舵面气动载荷的模拟等,用于辅助测试飞控系统的技术性能指标,达到改进设计,完善系统方案,节约成本的目的[1].采用负载模拟器对舵机系统进行测试,具有方便、安全、可控性好、可重复性高并能够实时调整等特点,相比实物破坏性试验具有突出的优点[2].从20世纪60年代起,各国就开始了对负载模拟器的研究,主要包括机械式、电液式以及电动式3种形式[3, 4, 5, 6, 7, 8].气动负载模拟器是以气体为工作介质,以力矩为被调整量的一类新型的、适合高速非高频的运动舵机的被动加载的伺服系统,具有成本低廉、较高的功率重量比、简单易操作、易维护等优点[9, 10, 11, 12, 13].在负载模拟器中,多余力是指由于舵机运动造成加载器的力矩加载跟踪误差.
电液负载模拟器由于油液的弹性模量大,舵机的主动运动对负载模拟马达形成的强迫流量会产生巨大的多余力[14, 15].对于电动负载模拟器来说,由于力矩电机转子的转动惯量通常较大,在舵机速度快速变化时,电机驱动滞后造成转子将被舵机拖动,转子惯性和反电动势形成较大的多余力矩.气动负载模拟器,由于气体的刚度较低,具有一定的缓冲效应,强迫流量不会形成较大多余力;另外由于气动马达的转子惯量小,被动运动也不会形成较大的惯性力矩,所以研究采用气动负载器实现高速舵机加载.由于气动系统的强非线性导致气动负载模拟器的多余力矩比较复杂,本文从线性和非线性两个方面分析了气动负载模拟器的多余力矩.
1 系统原理
1.1 系统结构示意图及实验平台
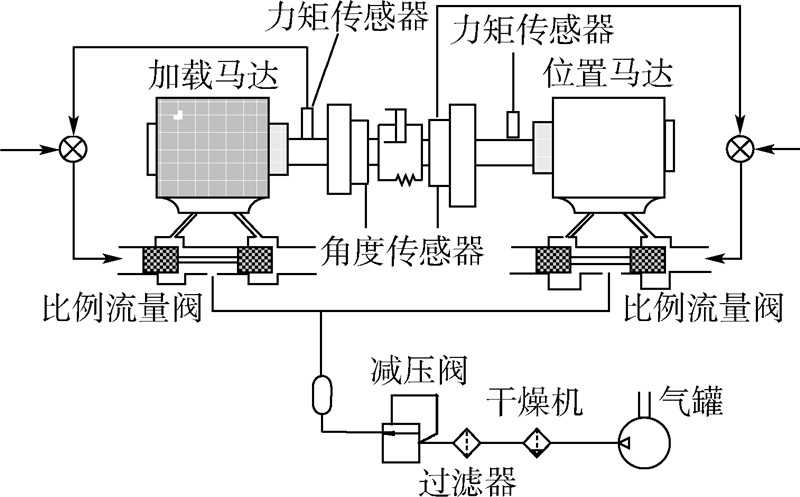
气动负载模拟器的结构原理图如图 1所示.右侧是舵机系统,模拟飞行器的舵机的主动运动,左侧是气动加载系统,主要由气源系统、气动加载马达、控制系统以及传感器(角度传感器、力矩传感器、压强传感器)等组成,用于给舵机系统进行加载.
1.2 数学模型
线性化模型会丢失系统的部分动态信息,但线性化模型对分析系统的机理及动态特性必不可少.气动伺服加载系统数学模型具体的线性化过程,本文在此不再赘述,可参考文献[8, 9],只对需要用到的公式进行说明.
气动马达1,2腔的状态方程描述如下:
式中
V1=Dm
(θ10+θ0);V2=Dm
(θ20+φ-θ0);
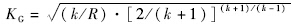
;∂,∂
1为介于k-1(k为等熵指数,取值为1.4)之间的系数,具体值视工作过程中发生的热力学过程而定;
R为气体常数;
T为环境温度;
S1in,
S1out,
S2in,
S2out分别为1,2腔的正开口和负开口面积;
Ps为气源压强;
P1,
P·
1分别为1腔压强及压强的导数;
P2,
P·
2分别为2腔压强及压强的导数;
V1,
V·
1分别为1腔的体积及体积的导数;
V2,
V·
2分别为2腔的体积及体积的导数;
Dm为摆动马达的弧度排量;
θ10,
θ20分别为1,2腔的初始角度;
φ为摆动马达的行程;
θ0为马达的角度位移量;
Pd表示节流口下游压力;
Pu表示节流口上游压力;
KG表示气体流量系数.在不考虑摩擦力的情况下,系统的动力学方程为
式中,
Mout为加载通道输出力矩,即传感器所测力矩;
Gε为力传感器扭转刚度;
θm为马达角位移;
θl为负载等效角位移;Δ
P为马达两腔压差;
Jm为马达转子惯量.其中
θl可以表示为
Jl为负载等效转动刚度;
Bl为负载等效阻尼系数;
Gl为负载等效扭转刚度,拉普拉斯变换后得到输出力矩的传递函数如下:
式中
s为微分算子,由于线性系统满足叠加原理,将式(6)分解成以下3个部分:
式中,
d=α1g2[1/(θ10+θ0)-1/(θ20+φ-θ0)];Se为有效开口面积;
K1=Gεa+Dm
e;由传递函数表达式可以看出,
Mout1部分与舵机的速度相关,是由于舵机的扰动引起的强迫流量所产生的力矩,称该部分为被动多余力矩;
Mout2部分与比例流量阀的开口有效面积有关,由于比例流量阀的主动控制所产生的力矩,称该部分为主动力矩;
Mout3部分与加载马达的转动惯量有关,还包括一些高阶项,称该部分力矩为惯性力矩.
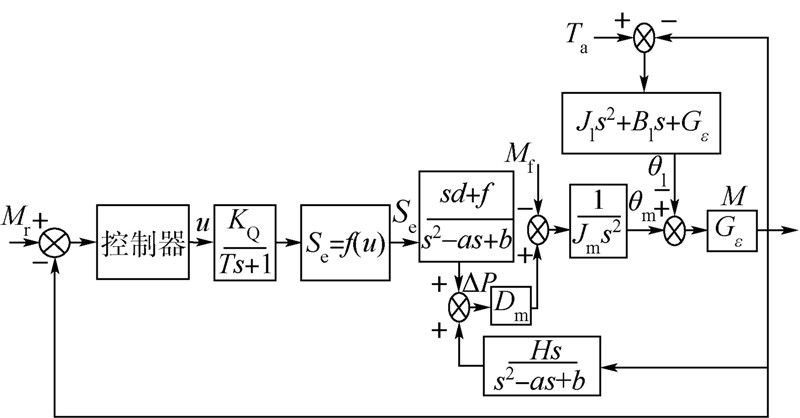
由于上述推导是在不考虑摩擦力矩的情况下进行的,所以加载系统的输出力矩还要考虑摩擦力矩的影响.由上述数学模型表达式可得气动负载模拟器的系统方框图,如图 2所示.
1.3 模型验证
为了验证数学模型的正确合理性,采用仿真实验对比进行验证.位置通道的指令分别为1Hz,60°正弦运动,加载通道的指令为0N·m的对顶加载实验.此时加载通道通过力矩传感器采集得到的力矩即为多余力矩.仿真和实验中均采用阀控气马达做位置伺服控制来模拟舵机系统和PI控制方法,其中实验控制参数:P=0.4,I=0.3;仿真控制参数:P=0.1,I=0.05.气动负载模拟器系统参数如表 1所示.
表 1 系统参数 Table 1 System parameters
| 气动马达 |
| 气源/MPa | 0.7
| | 排量/(m3/rad) | 3.2×10-4
| | 体积/L | 1.5
| | 惯量/(kg·m2) | 0.00084 |
|
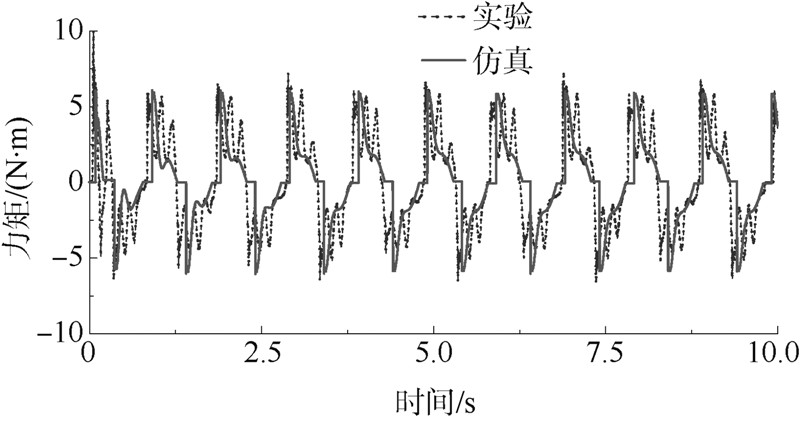
图 3为位置通道的指令为1Hz,60°正弦运动,加载通道的指令为0N·m的对顶加载测试多余力矩的仿真和实验曲线.从图 3可以看到,两种情况下的多余力矩吻合(约为5N·m),可以验证仿真结果的有效性,在实验情况的多余力矩出现了颤震的现象,这是由于实际系统的摩擦模型相对于仿真系统的摩擦模型更为复杂,实际系统的气源不稳定以及采样噪声等造成的,这对于系统多余力矩的分析不产生影响.
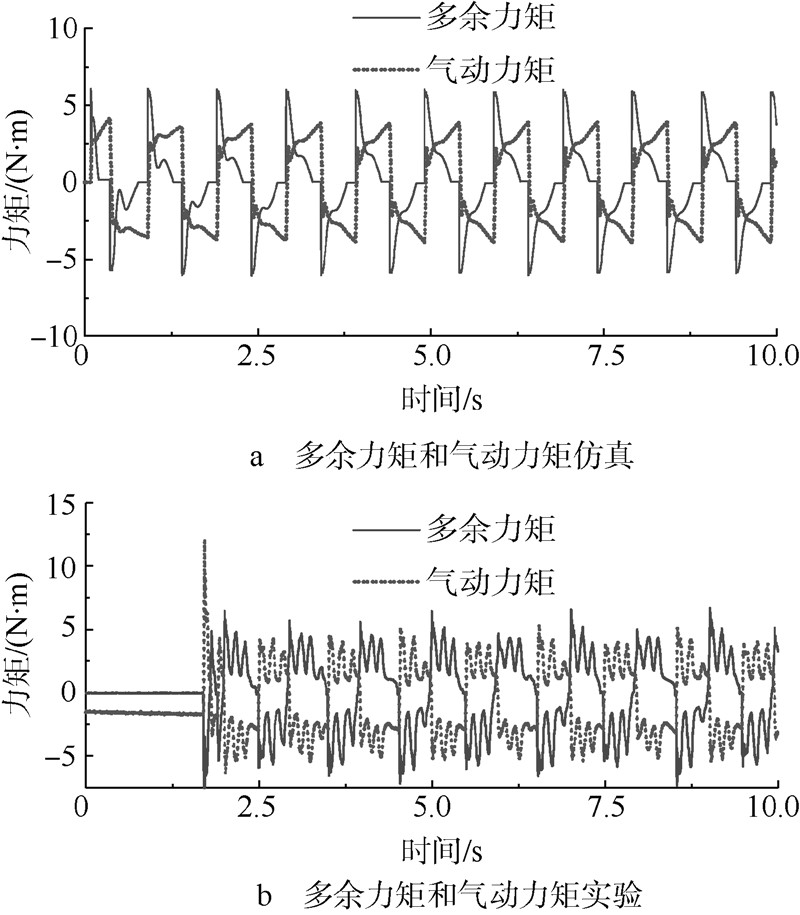
图 4a、图 4b分别是在位置通道的指令为1Hz,60°正弦运动,加载通道的指令为0N·m的对顶加载测试,多余力矩以及气动力矩(通过压差传感器计算得到)的仿真和实验曲线.图中气动力矩与多余力矩方向相反,是由于系统的主动控制产生,有一部分的摩擦力矩没有通过气动力矩抵消掉,这是因为位置通道存在摩擦力矩导致舵机通道的控制输出滞后,无法通过主动控制的作用实时抵消摩擦力矩的高阶部分.
仿真和实验在多余力矩与气动力矩的对比上分别吻合,进一步验证了数学模型的正确合理性.通过以上在不同工况下的实验和仿真的对比,可以证明数学模型的正确合理性.
2 气动负载模拟器多余力矩的分析
由于气动系统的非线性较强,为了更准确地分析气动负载模拟器的多余力矩的形成机理,以下采用非线性模型仿真对多余力矩进行定性分析.分别假设不同的工况共进行了6组仿真,具体的仿真说明如表 2所示.
表 2 仿真说明 Table 2 Simulation specification
强迫流量是指加载系统由于位置系统的突然运动对加载通道产生干扰而导致其位置的被动变化引起的流量,本组仿真假设在没有摩擦力矩的情况下,比较加载通道在0N·m(仿真2)控制和不控制的情况下(仿真3)的多余力矩的情况.在上述两组仿真情况下,力矩传感器采样得到的值即多余力矩,惯性力矩约为0.125N·m,根据式(9)可以得到,在没有摩擦力矩的情况下,加载系统的输出力矩表达式如下:
如果加载通道在没有控制的情况下,输出力矩的表达式为
式中,
Ms为力矩传感器采样即为加载系统输出
Mo;
J为加载系统惯量;
α为角加速度;Δ
P1为加载系统两腔被动压差;Δ
P2为加载系统两腔主动压差.仿真结果如
图 5所示.
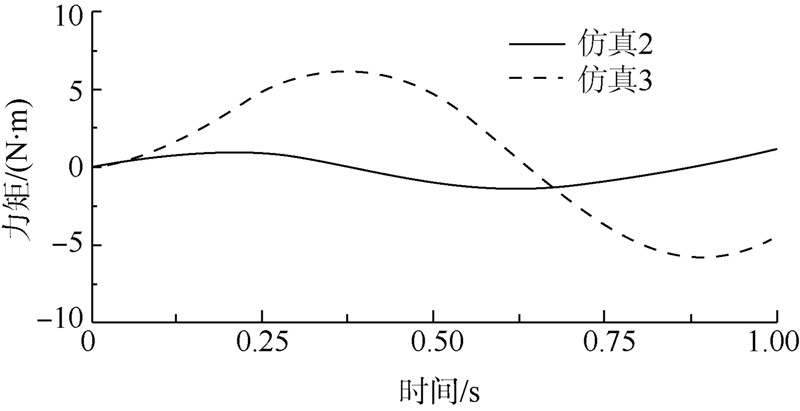
在上述仿真条件下,通过计算,系统的惯性力矩比较小,可以忽略,由强迫流量产生的多余力矩部分是真实存在的,但是又是不可测的一部分力矩,3组仿真是在忽略摩擦力矩的影响以及在开环的工况下进行的,该组仿真描述出了被动力矩的大小,通过和2组仿真结果的对比,可知由强迫流量产生的多余力矩的最大值为5N·m左右,在不考虑摩擦力矩的情况下,系统的多余力矩主要由强迫流量产生(惯性力矩的最大值约为0.125N·m).在不考虑摩擦力矩的情况下,气动伺服加载系统通过主动控制的作用可以抵消80%的由于强迫流量产生的多余力矩.
2.2 惯性力矩对多余力矩的影响
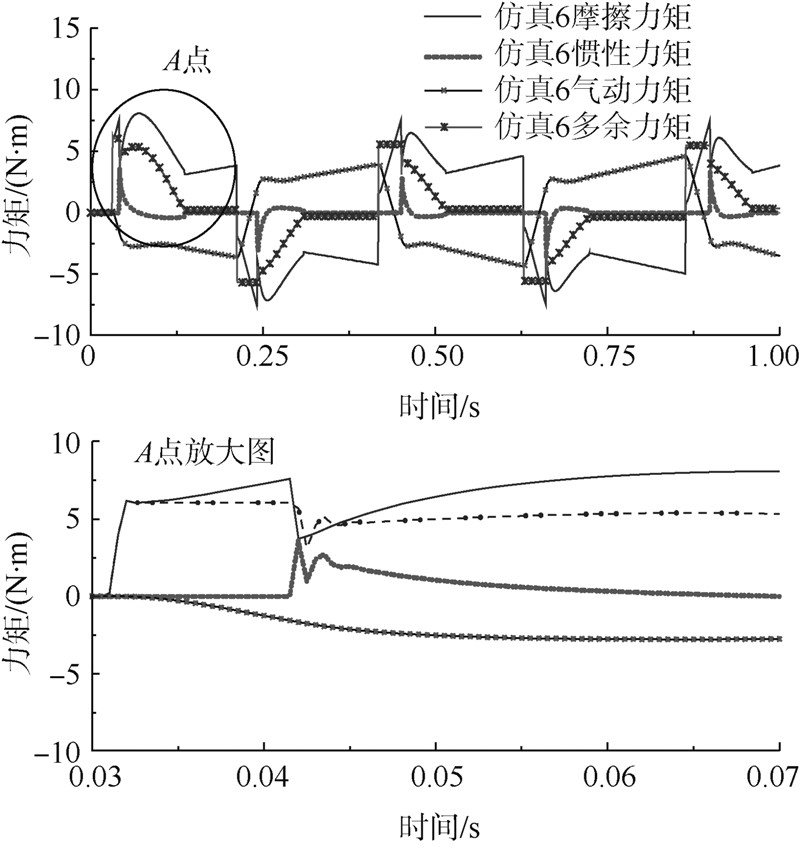
对于一种高速非高频运动的舵机的加载,在舵机运动的初始时刻,将会有一个比较大的冲击,产生较大的加速度,此时,惯性力矩对多余力矩的影响将不可忽略.为描述出这种运动工况,位置系统采用60°的方波指令,模拟高速非高频舵机的工况,加载系统采用0N·m指令(6组仿真)分析惯性力矩多余力矩的影响.仿真结果如图 6所示.
图 6是通过计算或测量得到的加载系统的各个力矩分量曲线,从图中可以看出,在初始时刻,多余力矩(仿真6多余力矩)与摩擦力矩(仿真6摩擦力矩)曲线重合,即这个阶段的多余力矩完全由摩擦力矩表征,加载通道在t=0.031s给出控制输出,经过一段时间的压差积累,在t=0.042s时有位移产生,此时摩擦力矩由静摩擦转换动摩擦,系统产生一个最大加速度(由于摩擦力矩的突变所致),产生最大的惯性力矩,最大值约为3.6N·m.此时的多余力矩表达式如下:
最大的惯性力矩出现在加载通道的摩擦力矩由静到动突变的时刻,此时加载通道的多余力矩小于系统处在静摩擦力矩的阶段.
2.3 摩擦力矩对多余力矩的影响
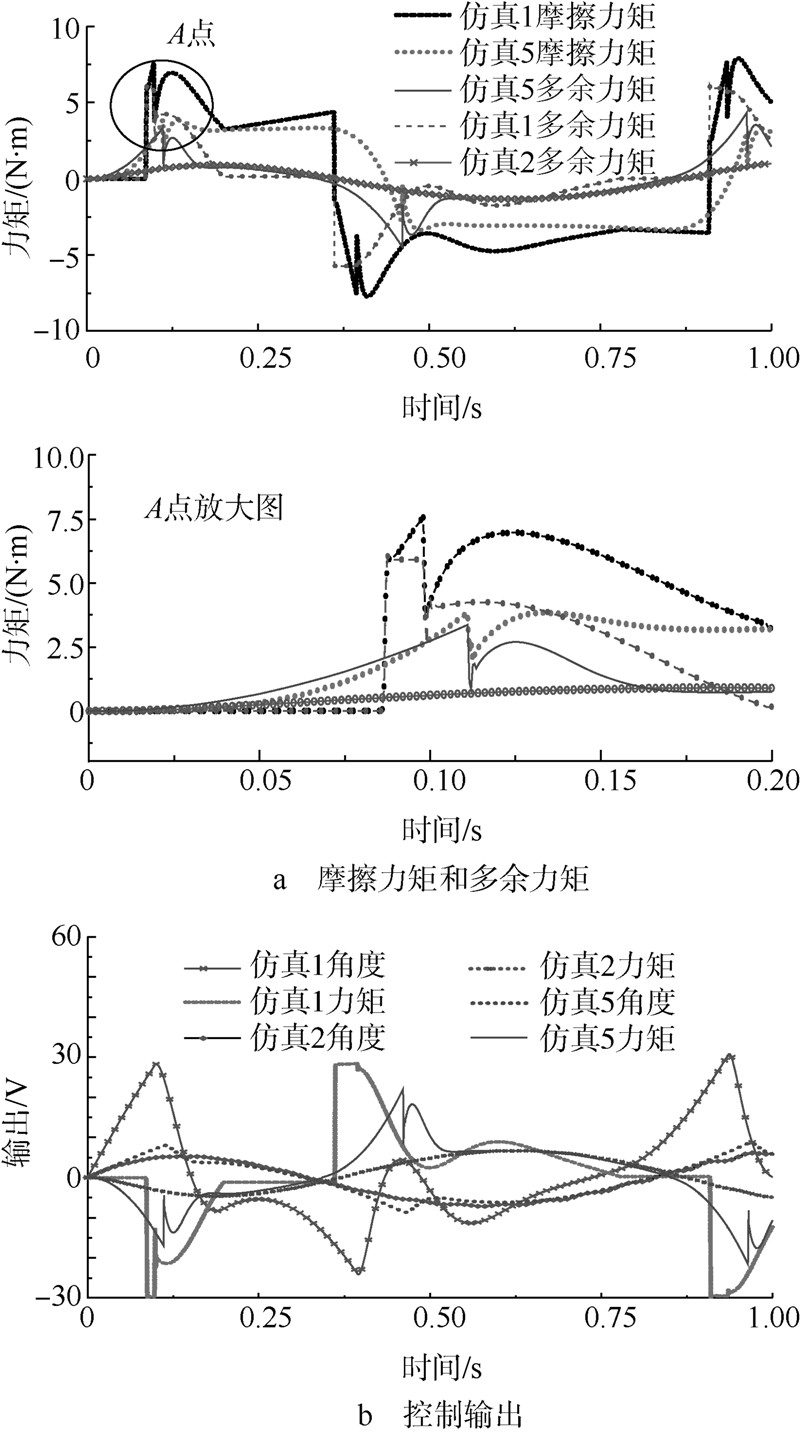
从图 6加载通道的各部分力矩曲线的对比分析,可以初步得出摩擦力矩对多余力矩的影响加大,为了更进一步地分析摩擦力矩对于多余力矩的影响,进行如下工况仿真分析:加载通道和位置通道同时存在摩擦力矩(仿真1);加载通道和位置通道同时没有摩擦力矩(仿真2);位置通道不存在摩擦力矩,只有加载通道存在摩擦力矩(仿真5),仿真详细说明参考表 2,仿真结果如图 7所示.
从图 7a可以看出,在舵机运动的起始和换向阶段,加载通道的多余力矩和摩擦力矩紧密相关,加载通道的主动控制作用的影响较小,如图 7a仿真1摩擦力矩及仿真5摩擦力矩采样所示;两通道的摩擦力矩均对加载通道的多余力矩有影响,对比仿真1多余力矩、仿真2多余力矩及仿真5多余力矩曲线,多余力矩的最大值分别为6.07,0.907和3.36N·m,可见,舵机通道的摩擦力矩对加载通道的多余力矩有一定的影响;由于摩擦力矩的存在(仿真1和5),系统的多余力矩中会有突变的现象,这对舵机通道的加载是不利的,而两组仿真中加载通道的多余力矩就比较光滑,且幅值较小.
从图 7b可以看出,若舵机通道存在摩擦,将导致加载通道的控制输出的延迟,进而导致两个通道的运动不同步,这也是影响多余力矩的重要因素,如果加载通道的控制输出及时给出,那么加载通道将有足够的时间通过主动控制的作用产生足够的压差以克服摩擦力矩和惯性力矩的影响,从而和舵机通道的运动保持同步,进而减小多余力矩.综合以上分析得出如下结论:摩擦力矩(舵机通道和加载通道的)是影响该气动负载模拟器多余力矩的重要影响因素,在加载通道起始和换向运动阶段,摩擦力矩几乎主导系统的多余力矩;摩擦力矩的存在使多余力矩产生突变现象,这一点对舵机的加载是不利的;舵机通道存在的摩擦力矩会影响加载通道控制输出的滞后,同时增大了加载系统的多余力矩.
3 结 论
通过以上对气动负载模拟器多余力矩的分析,得出如下结论:
1) 对于该气动负载模拟器来说,摩擦力矩是系统多余力矩的重要组成部分,其次是加载系统由于位置干扰引起的强迫流量产生的多余力矩,惯性力矩的影响相对较小.
2) 对于强迫流量,加载系统可以通过主动控制将其影响减小到理想的误差范围内.
3) 摩擦力矩影响了系统的动态控制品质,在加载通道起始和换向运动阶段,摩擦力矩几乎主导系统的多余力矩;摩擦力矩的存在使多余力矩产生突变现象,这一点对舵机的加载是不利的;舵机通道存在的摩擦力矩会影响加载通道控制输出的滞后,同时增大了加载系统的多余力矩.因此减小加载通道的控制输出的相对滞后以及改变或改善摩擦力矩产生的突变现象是摩擦力矩补偿研究的方向.
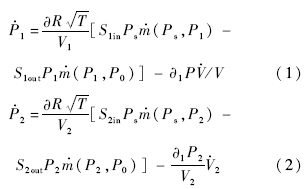
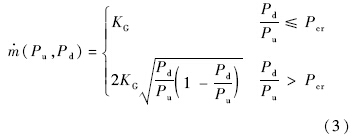
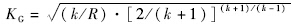 ;∂,∂1为介于k-1(k为等熵指数,取值为1.4)之间的系数,具体值视工作过程中发生的热力学过程而定;R为气体常数;T为环境温度;S1in,S1out,S2in,S2out分别为1,2腔的正开口和负开口面积;Ps为气源压强;P1,P·1分别为1腔压强及压强的导数;P2,P·2分别为2腔压强及压强的导数;V1,V·1分别为1腔的体积及体积的导数;V2,V·2分别为2腔的体积及体积的导数;Dm为摆动马达的弧度排量;θ10,θ20分别为1,2腔的初始角度;φ为摆动马达的行程;θ0为马达的角度位移量;Pd表示节流口下游压力;Pu表示节流口上游压力;KG表示气体流量系数.在不考虑摩擦力的情况下,系统的动力学方程为
;∂,∂1为介于k-1(k为等熵指数,取值为1.4)之间的系数,具体值视工作过程中发生的热力学过程而定;R为气体常数;T为环境温度;S1in,S1out,S2in,S2out分别为1,2腔的正开口和负开口面积;Ps为气源压强;P1,P·1分别为1腔压强及压强的导数;P2,P·2分别为2腔压强及压强的导数;V1,V·1分别为1腔的体积及体积的导数;V2,V·2分别为2腔的体积及体积的导数;Dm为摆动马达的弧度排量;θ10,θ20分别为1,2腔的初始角度;φ为摆动马达的行程;θ0为马达的角度位移量;Pd表示节流口下游压力;Pu表示节流口上游压力;KG表示气体流量系数.在不考虑摩擦力的情况下,系统的动力学方程为