Download PDF  
文章快速检索  
  高级检索
引用本文
曹龙, 曹义华, 李春华. 直升机-吊挂耦合系统平衡特性和稳定性分析[J]. 北京航空航天大学学报, 2014, 40(9): 1219-1224
Cao Long, Cao Yihua, Li Chunhua. Equilibrium characteristics and stability analysis of helicopter-slung-load coupling system[J]. Journal of Beijing University of Aeronautics and Astronsutics, 2014, 40(9): 1219-1224.
直升机-吊挂耦合系统平衡特性和稳定性分析
曹龙1, 曹义华1, 李春华2    
1. 北京航空航天大学 航空科学与工程学院, 北京 100191;
2. 中航工业中国直升机设计研究所, 景德镇 333001
收稿日期:2013-10-10; 网络出版日期: 2014-03-14
作者简介: 曹龙（1988-），男，湖北大悟人，博士生，caolong.buaa@gmail.com.
摘要：基于单质点吊挂假设，建立了直升机-吊挂耦合系统的非线性动力学模型。在该假设下，吊挂将引入额外的自由度和约束，使运动方程增加4阶，且为隐式的微分代数方程组。通过将惯性力中的广义加速度项与广义速度的二次项分离，可将运动方程转化为显式的微分方程组。针对无吊挂的直升机本体和直升机-吊挂耦合系统这两种模型，采用直接数值方法，计算了它们以不同速度做零侧滑定直平飞的配平状态，并结合飞行试验数据进行对比。进一步对两种模型进行了小扰动线化处理，分析其运动模态并进行对比。结果表明，单质点吊挂会给系统引入两个新的运动模态，使得吊挂两个自由度上的运动与直升机高度响应产生耦合，同时改变直升机本体各个模态的特性，会使部分模态响应品质变坏。
关键词： 直升机     吊挂载荷     耦合     配平     稳定性     模态    
Equilibrium characteristics and stability analysis of helicopter-slung-load coupling system
Cao Long1, Cao Yihua1, Li Chunhua2     
1. School of Aeronautic Science and Engineering, Beijing University of Aeronautics and Astronautics, Beijing 100191, China;
2. AVIC China Helicopter Research and Development Institute, Jingdezhen 333001, China
Abstract:A nonlinear dynamical model of the helicopter-slung-load coupling system was presented, based on single mass-point hypothesis. Under this hypothesis, the consideration of the slung-load brought in extra degrees of freedom and constraints, which made the equations of motion increased by 4 orders, and being a set of implicit differential algebraic equations. By distinguishing the generalized acceleration terms from the quadratic generalized speed terms in the inertia forces, the equations of motion can be turned into a set of explicit ordinary differential equations. For the helicopter model and the helicopter-slung-load model, trim states for zero-side-slipping forward flight were first computed, using direct numerical approach, and the results were compared with flight test data. Then, both of the two models were linearized under small-perturbed conditions, and modal decomposition was performed on these linearized models. Results show that 2 new dynamical modes would be introduced by the single-mass-point slung-load. Motions of the slung-load's 2 degrees of freedom would be coupled with the helicopter's altitude response, and modify the characteristics of helicopter's inherence modes, make some of them worse.
Key words: helicopter     slung-load     coupling     trim     stability     mode    

吊挂载荷飞行是直升机相比于其他种类飞行器所特有的一项功能,它基本不受货物外形、体积等的限制,且能够克服很多地形条件的制约.

国外自20世纪70年代起,就有关于直升机

吊挂飞行的研究,文献[1, 2]中对此都有较为系统的综述,且这两篇文献本身也都是这一领域的重要成果.文献[1]采用了CH-47直升机的早期型号,并专门对吊挂进行了风洞实验.文献[2]采用了文献[3]中记载的CH-53A/D直升机的数学模型,考虑了“倒V型”刚性绳索、“倒Y型”刚性绳索和“倒Y型”弹性绳索这3种不同连结方式,模型推导非常详细.但是由于受制于原始数据条件和当时的计算机硬件水平,其数值处理都是对线化以后的模型进行的.文献[4, 5]中将吊挂视为质点,较系统地分析了吊挂的平衡和运动模态,但有关吊挂对直升机本体运动的影响问题则处理得比较粗糙.文献[6, 7]分别用数值仿真和飞行试验的方法研究了带吊挂的直升机本体运动模态特性.

近年来,国内陆续有直升机吊挂方面的研究工作开展[8, 9, 10, 11, 12, 13].其中文献[8]在文献[4]的基础上,研究了吊挂的引入对直升机本体气动导数的影响.文献[10, 11, 13]又以文献[8]为基础,进一步开展了弹性绳索、操稳特性和吊挂构型等方面的研究.

本文有关吊挂运动模型的部分仍是以文献[4]为基础,但重新给出了完整的直升机-吊挂耦合系统动力学模型,在此基础上计算其平衡状态,并做稳定性和模态分析,以研究直升机与吊挂之间的相互耦合. 1 直升机-吊挂耦合动力学模型 1.1 直升机本体模型 1.1.1 模型简介

本文中计算所使用的CH-53A/D直升机数学模型来自文献[14].模型中考虑了旋翼诱导入流和发动机调速器的动态效应,使得直升机本体模型达到15阶.在本文的计算中,这两部分模型采取准静态处理而加以简化,使得直升机本体模型仍为9阶,与传统的6自由度飞行动力学模型相同.

模型中产生气动力的部件有3个:主旋翼、尾旋翼和机身.两个旋翼的气动力计算方法基于经典叶素理论,除旋翼以外的其他所有部件(包括平尾和垂尾)都计入机身内,提供了完整的风洞试验数据. 1.1.2 非线性全量方程

直升机本体非线性动力学全量方程在机体的体轴系内建立,衡量直升机当前状态的变量包括速度v=(u,v,w)T、姿态角θ=(φ,θ,ψ)T和姿态角速度ω=(p,q,r)T.飞行员提供的操纵输入为u=(θ0m,A′1,B′1,θ0t)T,包括主/尾旋翼的总距和主旋翼的纵/横向周期变距.

直升机质心平动微分方程为

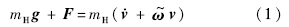
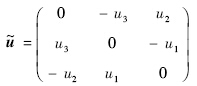
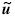其中,mH为直升机总质量;向量g为重力加速度在体轴系内的表示;F为直升机各部件气动力的合力,它是所有状态变量和操纵输入的函数;ω~为角速度向量ω的叉乘张量.对于三维向量u=(u1,u2,u3)T,其叉乘张量(以下均用波浪号表示)定义为如下矩阵：
此时,数学形式上,u与任意向量v的叉乘(矢量积u×v)恰好等于矩阵与向量v的乘积.

直升机绕质心的转动微分方程为

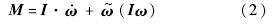
其中,M为直升机各部件气动力矩的合力矩,它也是所有状态变量和操纵输入的函数;I为直升机机身的惯性张量.

另外,姿态定义采用欧拉角的方案,角速度之间满足如下几何关系:

这里,C(θ)为欧拉转换矩阵,其具体形式可参考文献[14].式(1)~式(3)形成一个封闭的微分方程组,即为直升机本体非线性全量方程. 1.2 直升机-吊挂耦合系统动力学模型

本文采用的吊挂动力学模型基于文献[4].吊挂假设为质点,其所受的气动力仅有当地气流方向的准静态阻力,忽略绳索气动力.绳索零质量、完全刚性,且时刻处于绷紧状态.故绳索总是直线,连结着直升机上的挂点和吊挂质心,提供一个双侧的完整约束. 1.2.1 吊挂动力学分析

衡量吊挂位移的广义坐标(吊挂姿态角)在直升机体轴系内定义,如图 1所示,θl和φl分别称为吊挂的后摆角和侧摆角.注意,这两个角度的正方向与坐标轴方向不遵循右手法则.另记向量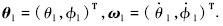

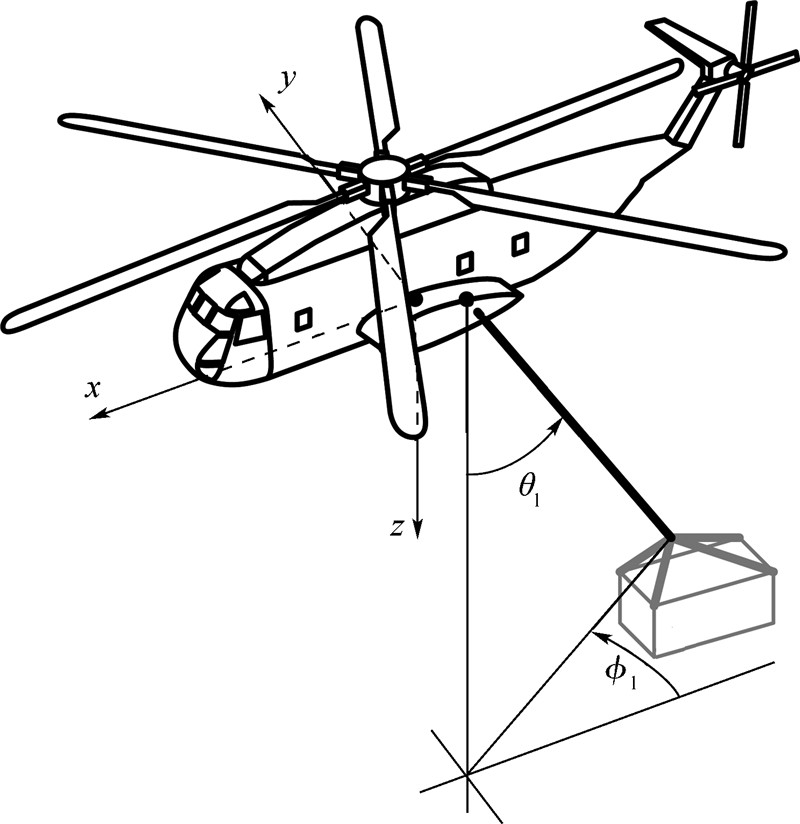图 1 直升机体轴系与吊挂姿态定义Fig. 1 Definition of the helicopter body reference frame and the attitude angles of slung-load
图选项

吊挂质心在体轴系中的坐标为

其中,rh为机身挂点的坐标,是常量;rl是绳索两端的相对位移,其表达式为
这里,l为绳索长度.其一阶和二阶时间导数不难计算,分别为
其中

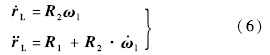
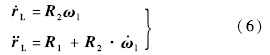
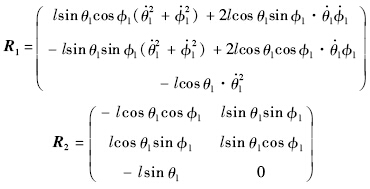
吊挂的绝对速度在体轴系中的表达式为

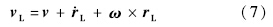
绝对加速度在体轴系中的表达式为

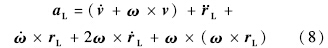
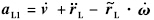它可看作两项的叠加,即广义加速度变量的一次齐次形式和广义速度变量的二次齐次形式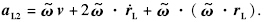

吊挂所受气动阻力在体轴系中的表达式为

其中,ρ为空气密度;SL为吊挂的迎风阻力面积.

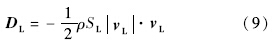
吊挂作用在直升机上的合力为

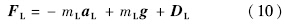
合力方向应与绳索方向相同,故有

于是,吊挂作用在直升机上的合力矩为

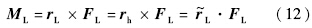
1.2.2 耦合系统的非线性全量方程

直升机-吊挂耦合系统的平动和转动微分方程分别为

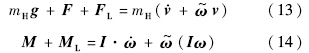
将式(4)~式(8)、式(10)和式(12)代入,式(11)、式(13)和式(14)可统一为如下矩阵形式:

此方程中,只有等号左侧的向量含有加速度项.

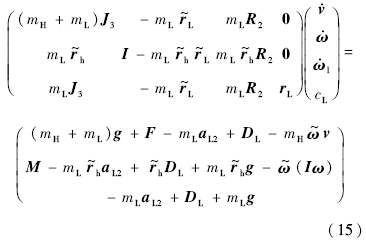
另外,还有

式(3)、式(15)和式(16)也形成一个封闭的微分方程组,即为直升机-吊挂耦合系统非线性全量方程. 2 配平计算结果

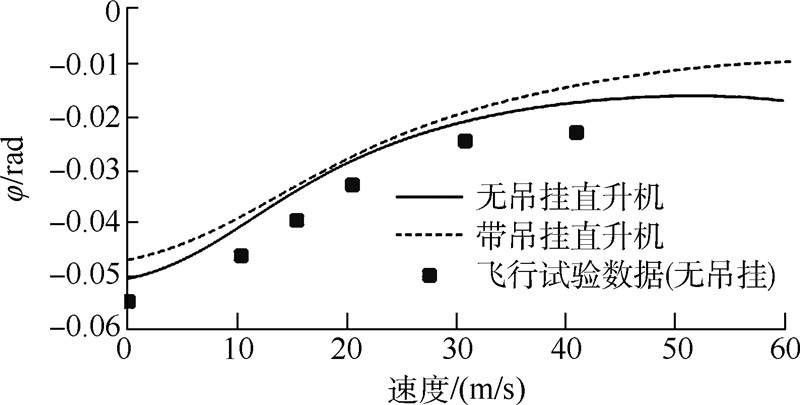
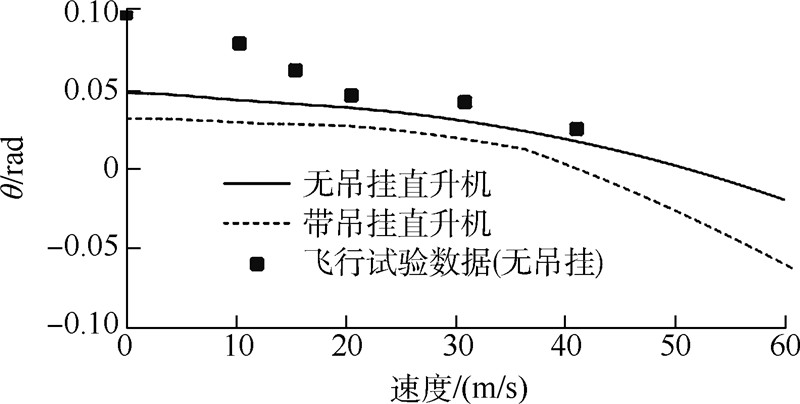
图 2~图 8给出了无吊挂的直升机本体和直升机-吊挂耦合系统这两种模型的配平计算结果,均为无侧滑的定直平飞,速度范围0~60m/s(前进比0~0.28).计算过程的部分参数取值如表 1所列,有关直升机的参数均来自文献[14].图中同时还提供了无吊挂情形的飞行试验数据[3].

图 2 配平计算结果:滚转角Fig. 2 Trim result:roll angle
图选项
图 3 配平计算结果:俯仰角Fig. 3 Trim result:pitch angle
图选项
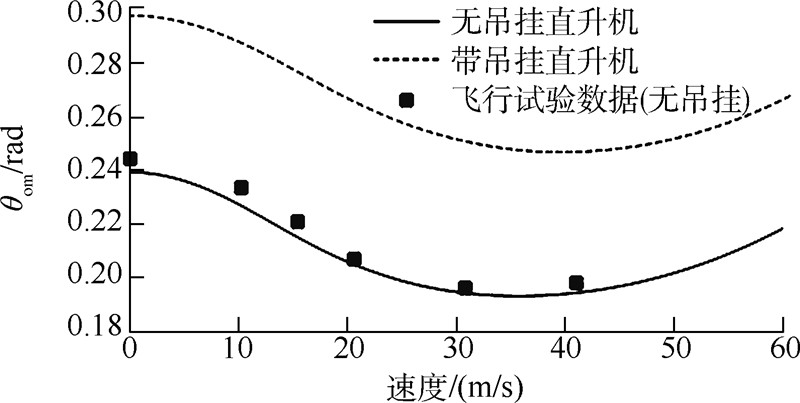图 4 配平计算结果:主旋翼总距Fig. 4 Trim result:main rotor collective pitch
图选项
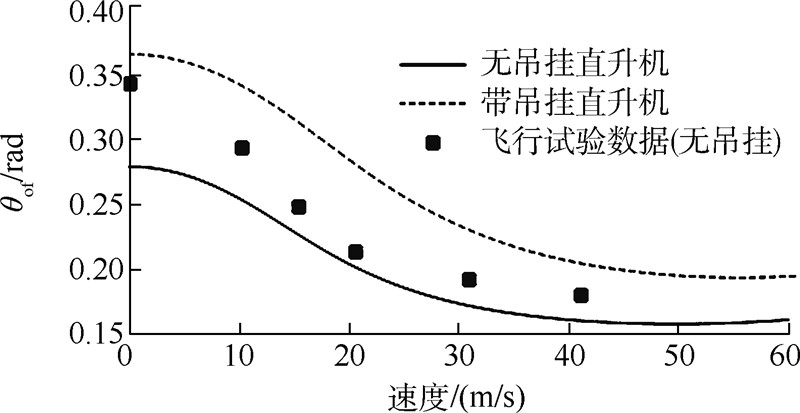图 5 配平计算结果:尾旋翼总距Fig. 5 Trim result:tail rotor collective pitch
图选项
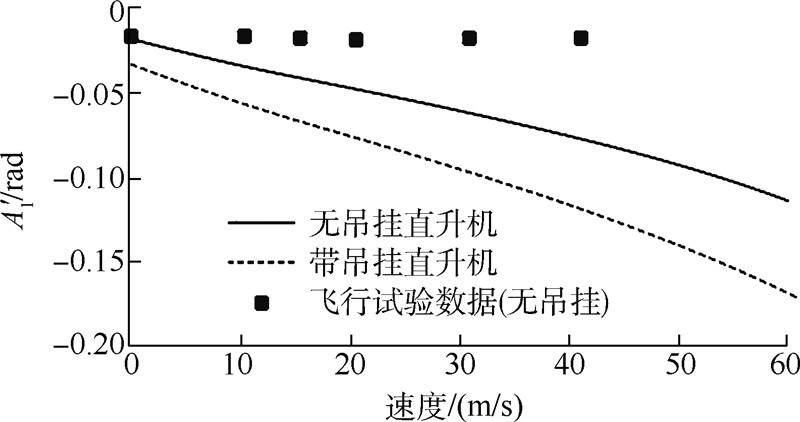图 6 配平计算结果:横向周期变距Fig. 6 Trim result:lateral cyclic control
图选项
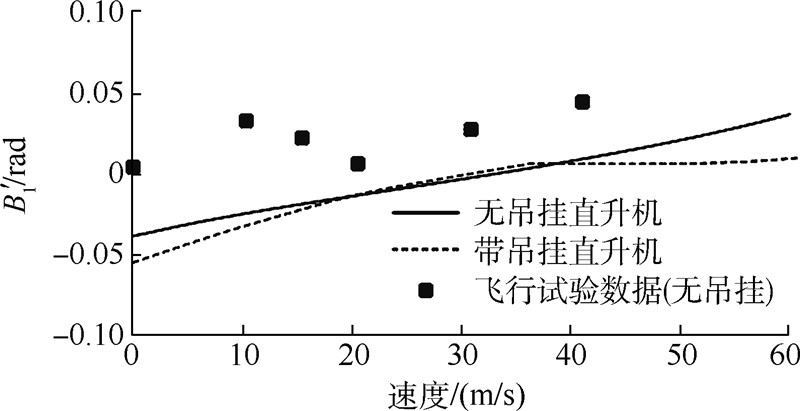图 7 配平计算结果:纵向周期变距Fig. 7 Trim result:longitudinal cyclic control
图选项
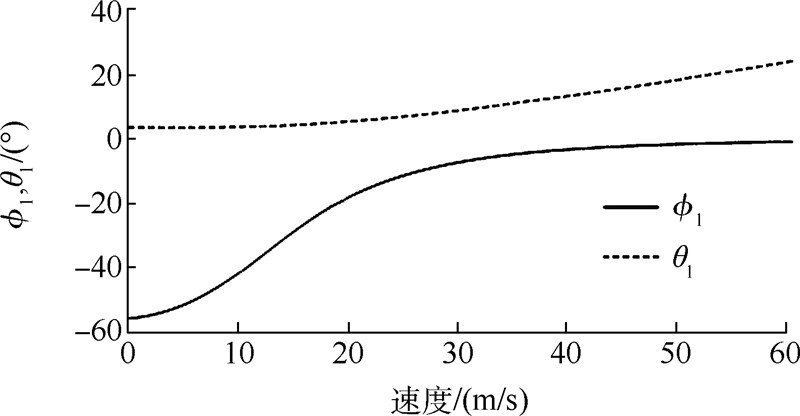图 8 配平计算结果:吊挂后摆角和侧摆角Fig. 8 Trim result:longitudinal and lateral swing angles of slung-load
图选项
表 1 CH-53部分参数取值 Table 1 Parameters of the CH-53 helicopter
参数数值
主旋翼转速/(rad/s)19.30
主旋翼半径/m11.01
主旋翼实度0.1145
直升机自重/kg15227
机身转动惯量Ixx/(kg·m2)48891
机身转动惯量Iyy/(kg·m2)239491
机身转动惯量Izz/(kg·m2)223361
机身转动惯量Ixz/(kg·m2)22518
吊挂质量/kg8000
吊挂绳索长度/m40
吊挂迎风阻力面积/m218
挂点坐标(体轴系)/m(0,0,1.94)
表选项

从图 2~图 8中可以看到,除周期变距操纵量以外,其他的计算结果均与飞行试验吻合得很好.

相比于无吊挂情形,直升机吊挂飞行状态下两个旋翼都需要更大的总距输入,其原因是显而易见的.

吊挂飞行状态下的滚转角比无吊挂时更小,当然这里有的前提条件就是CH-53直升机主旋翼为右旋旋翼,且在体轴系中绳索挂点位于质心正下方.右旋旋翼前飞时,右侧升力较大,机身会有一个负的滚转角(向左滚转),于是挂点会转动到右侧,于是吊挂载荷会提供一个正的滚转力矩,将滚转姿态往回拉.吊挂飞行状态下的俯仰角比无吊挂时更大,这主要是因为吊挂气动阻力会给机身提供一个低头力矩. 3 运动模态及稳定性分析 3.1 无吊挂直升机的运动模态

无吊挂的直升机运动模态如表 2所示.其中,本文计算结果基于直升机本体非线性全量方程的小扰动线化模型,线化过程采取有限差分近似.

表 2 无吊挂直升机运动模态特征根(速度60kn) Table 2 Eigenvalues of dynamical modes of the motion of helicopter without slung-load (60kn)
模态飞行试验数据[3]本文计算结果
长周期0.0734±0.2971i-0.0355±0.4551i
短周期-0.6839±0.0753i-0.7321±0.4655i
荷兰滚-0.2039±1.0096i-0.0834±1.0663i
滚转-1.63-0.3994
螺旋-0.121-0.1269
偏航00
表选项

从表 2中可以看到,除了长周期模态的稳定性以外,计算结果与飞行试验数据定性上是相符合的. 3.2 直升机-吊挂的运动模态

直升机-吊挂耦合相对于直升机本体,额外引入了4个状态变量,即θl,φl和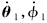.因此,模型提高了4阶,相应的也会多出4个特征根和一些运动模态.

直升机-吊挂系统耦合运动所有模态的特征值和特征向量如表 3所示.这些特征向量的13个分量依照如下次序,一一对应于每一个状态变量:u,v,w,p,q,r,φ,θ,ψ,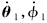,θl以及φl.注意,对于每一个复特征值(及其特征向量),都有与之共轭的另一个复特征值(及其特征向量)未列入表 3中,它们组成一个耦合振荡模态.此外,还有一个零特征值也未列入表 3中,其特征向量只有第9个分量(对应于偏航角ψ)非零,它就对应于中立稳定的偏航模态.

表 3 直升机-吊挂耦合系统运动模态(速度60kn) Table 3 Eigenvalues of dynamical modes of the motion of helicopter with slung-load (60kn)
特征值0.1150+1.0239i0.0484+0.2228i-0.1783+0.7921i-0.35691.3896-2.0230+1.2485i-0.1798+0.1044i
特征向量分量u 0.2908+0.4271i-0.8428-0.3214-0.3074i-0.46860.2816-0.1901+0.2889i 0.1725+0.1769i
v 0.1833-0.2627i-0.3591+0.3427i-0.6148+0.1191i0.1106-0.0459-0.0861+0.1105i-0.9001
w0.7867 0.0024+0.1837i-0.63670.87200.9070.8038-0.1198+0.0315i
p 0.0055-0.0018i-0.0099+0.0025i 0.0027-0.0017i-0.0138-0.0376-0.0145-0.0680i 0.0327-0.0159i
q 0.0164+0.0244i-0.0039+0.0033i-0.0082-0.0158i0.00150.0494-0.0403+0.0364i-0.0010+0.0002i
r-0.0092-0.0064i 0.0033+0.0144i-0.0005+0.0159i0.0153-0.003 0.0005+0.0138i-0.0568+0.0022i
φ-0.0013-0.0054i 0.0027+0.0449i-0.0025-0.0029i0.0380-0.0271-0.0098+0.0275i-0.1701-0.0107i
θ 0.0252-0.0130i 0.0117+0.0197i-0.0164+0.0141i-0.00490.0355 0.0225-0.0042i 0.0091+0.0042i
ψ-0.0076+0.0084i 0.0647-0.0011i 0.0195-0.0039i-0.0427-0.0028 0.0024-0.0050i 0.2416+0.1279i
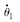0.0310+0.0381i 0.0029-0.0101i-0.0169-0.0259i-0.01990.0956-0.0607+0.0650i-0.0045-0.0137i
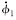0.0472+0.0163i-0.0009-0.0031i-0.0072-0.0163i0.0078-0.2239-0.1114-0.3925i 0.0001+0.0003i
θl 0.0401-0.0258i-0.0407-0.0218i-0.0266+0.0273i0.05570.0688 0.0361-0.0099i-0.0144+0.0677i
φl 0.0209-0.0438i-0.0144+0.0010i-0.0176+0.0131i-0.0219-0.1612-0.0468+0.1651i 0.0002-0.0015i
模态长周期短周期荷兰滚滚转螺旋吊挂侧摆与高度
耦合模态		吊挂后摆与高度
耦合模态
不稳定不稳定稳定稳定不稳定稳定稳定
表选项

从计算结果中可以看到,吊挂载荷会引入两个周期运动模态,从特征向量各分量幅值关系来看,它们分别是吊挂后摆角与高度的耦合、吊挂侧摆角与高度的耦合.吊挂作用在直升机上的力主要沿高度方向,这自然会使得直升机的高度响应比无吊挂的情形要剧烈的多,所以出现这两个耦合模态是合理的.两个模态都是稳定的,这也很好理解.因为吊挂可以粗略地看成一个圆锥摆,总有一个稳定的平衡位置.侧摆耦合模态的阻尼比为0.8510,后摆耦合模态的阻尼比为0.865,阻尼特性都比较好.相比于无吊挂的情况,吊挂的引入还在一定程度上改善了本体荷兰滚模态的阻尼特性.侧摆耦合模态收敛速度比后摆耦合模态快很多,这是因为前飞时,吊挂气动阻力对侧摆有明显的抑制作用,对后摆则没有.

尽管两个吊挂模态本身都是稳定的,但引入吊挂以后,却使得直升机本体的长/短周期和螺旋模态都变得不稳定了.尤其是螺旋模态,倍幅时间只有约0.5s.这将严重影响系统的飞行品质. 4 结 论

本文基于单质点吊挂假设,在已有的CH-53直升机数学模型的基础上,建立了直升机-吊挂耦合系统的非线性动力学模型,并通过适当的数学技巧在一定程度上简化了方程的形式.

针对直升机-吊挂耦合系统进行了配平计算,并与直升机本体(不带吊挂)的相应结果以及飞行试验数据进行了对比.大部分计算结果均与飞行试验数据吻合.

在配平计算的基础上,本文进一步对直升机-吊挂耦合系统进行了稳定性和模态特性分析.结果表明,吊挂的引入会使系统产生两个全新的周期性模态,分别是吊挂后摆(纵向运动)与直升机高度响应的耦合模态,以及吊挂侧摆(横向运动)与直升机高度响应的耦合模态,从而影响直升机本体的纵向运动特性.新产生的两个模态本身是稳定的,且具有较为良好的频率和阻尼特性.但引入吊挂后,直升机本体的纵向长、短周期模态均变得不稳定,横向螺旋模态发散速度也大大增加.

参考文献
[1] Sampath P.Dynamics of a helicopter-slung load system[D].Maryland:University of Maryland,1980
[2] Ronen T.Dynamics of a helicopter with a slung load [D].Stanford:Stanford University,1986
[3] Heffley R K,Jewell W F,Lehman J M,et al.A compilation and analysis of helicopter handling qualities data,volume one:data compilation[R].NASA-CR-3144,1980
[4] Fusato D,Guglieri G,Celi R.Flight dynamics of an articulated rotor helicopter with an external slung load [J].Journal of the American Helicopter Society,2001,46(1):3-13
Click to display the text
[5] Thanapalan K,Wong T M.Modeling of a helicopter with an under-slung load system[C]//Proceedings of the 29th Chinese Control Conference.Piscataway,NJ:IEEE,2010:1451-1456
[6] Stucky R A.Mathematical modelling of helicopter slung-load system[R].DSTO-TR-1257,2002
[7] Cicolani L S,Cone A,Theron J N.Flight test and simulation of a cargo container slung load in forward flight[J].Journal of the American Helicopter Society,2009,54(3):032006-1-18
Click to display the text
[8] 崔瑛.直升机吊挂飞行稳定性分析[D].南京:南京航空航天大学,2005 Cui Ying.Stability analysis of a helicopter with an external slung load[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2005(in Chinese)
Cited By in Cnki (2)
[9] 吴鹏,马成江,朱国民.直升机吊挂飞行动力学建模与分析[J].直升机技术,2010,165(4):33-36 Wu Peng,Ma Chengjiang,Zhu Guomin.Flight dynamics modeling and handling quality analysis of helicopter with slung-load[J].Helicopter Technique,2010,165(4):33-36(in Chinese)
Cited By in Cnki (1)
[10] 齐万涛,陈仁良.直升机吊挂飞行稳定性和操纵性分析[J].南京航空航天大学学报,2011,43(3):406-412 Qi Wantao,Chen Renliang.Stability and control characteristic analysis for flight of helicopter with slung-load[J].Journal of Nanjing University of Aeronautics and Astronautics,2011,43(3):406-412(in Chinese)
Cited By in Cnki
[11] 崔利,曹义华,李国知.直升机吊挂飞行平衡、稳定性与操纵性研究[J].航空动力学报,2010,25(10):2307-2311 Cui Li,Cao Yihua,Li Guozhi.Studies on trims,stability,and controllability of helicopter with slung-load[J].Journal of Aerospace Power,2010,25(10):2307-2311(in Chinese)
Cited By in Cnki (4) | Click to display the text
[12] 马超,曹义华,徐忠达.直升机吊挂流场数值模拟与尾鳍设计分析[J].北京航空航天大学学报,2012,38(5):654-658 Ma Chao,Cao Yihua,Xu Zhongda.Numerical simulation of helicopter slung-load flow field and fins design[J].Journal of Beijing University of Aeronautics and Astronautics,2012,38(5):654-658(in Chinese)
Cited By in Cnki (1)
[13] 曹龙,曹义华,马超,等.直升机吊挂构型计算及稳定性分析[J].北京航空航天大学学报,2012,38(6):711-714 Cao Long,Cao Yihua,Ma Chao,et al.Analysis on stability and structure computation of helicopter with slung-load[J].Journal of Beijing University of Aeronautics and Astronautics,2012,38(6):711-714(in Chinese)
Cited By in Cnki (1)
[14] Sturgeon W R.A mathematical model of the CH-53 helicopter[R].NASA TM-81238,1980
[15] Ostroff A J,Downing D R,Rood W J.A technique using a nonlinear helicopter model for determining trims and derivatives[R].NASA TN-D-8159,1976
[16] Ananthkrishnan N,Sinha N K.Level flight trim and stability analysis using extended bifurcation and continuation procedure[J].Journal of Guidance,Control,and Dynamics,2000,24(6):1225-1228
Click to display the text
http://dx.doi.org/10.13700/j.bh.1001-5965.2013.0561
北京航空航天大学主办。
0

文章信息

曹龙, 曹义华, 李春华
Cao Long, Cao Yihua, Li Chunhua
直升机-吊挂耦合系统平衡特性和稳定性分析
Equilibrium characteristics and stability analysis of helicopter-slung-load coupling system
北京航空航天大学学报, 2014, 40(9): 1219-1224
Journal of Beijing University of Aeronautics and Astronsutics, 2014, 40(9): 1219-1224.
http://dx.doi.org/10.13700/j.bh.1001-5965.2013.0561

文章历史

收稿日期：2013-10-10
网络出版日期: 2014-03-14

相关文章

工作空间