2. 第二炮兵装备研究院, 北京 100085
2. The Second Artillery Equipment Institude, Beijing 100085, China
相对于传统飞行器,高超声速飞行器具有飞行包线大、参数快变以及由飞行环境复杂等因素造成的参数强不确定性等特点,仅设计一套控制器难以兼顾大包线范围内的性能要求.目前,国内外针对全包线控制器的设计大多数采用传统的增益调参方法,基本思想是将包线划分为一系列子区域,每个子区域选取标称状态点设计一个线性控制器,即采用多个线性控制器来满足全包线的控制需求.但关于全飞行包线内如何实现区域划分,还没有一套成熟的理论可以遵循.
文献[1,2]分别按照动压等高线和高度、马赫数进行包线划分,其很大程度依赖设计者经验;文献[3,4,5]就发动机控制问题基于线性模型特征值或发动机参数设计衡量指标,依此判定标称点所能代表的区域;文献[6,7]就无人机控制问题分别采用模糊聚类划分原理和基于奇异值设计衡量指标进行包线划分.以上所设计的指标均能对包线划分提供一定的参考,但多凭借经验及反复迭代验证来进行分区,较耗时耗力.
间隙度量是一种不同于范数度量的系统度量概念,最先由Hausdorf提出,随后Zames和El-Sakkary利用间隙度量建立了在保证闭环系统稳定下所能容许的最大不确定度量化指标[8,9,10].并且El-Sakkary的研究显示,相对于基于范数的度量指标,间隙度量更适合用来衡量两个线性系统之间的差异大小,因而适合作为评价线性系统差异的指标.针对高超声速飞行器姿态控制问题,本文提出以间隙度量作为参考指标,指导飞行包线内的区域划分.本文简要介绍了间隙度量的理论,利用间隙度量分析得到大包线模型特性变化规律,指导完成了包线划分,并根据包线划分结果进行控制器设计验证,证实了划分结果的合理性. 1 基于间隙度量的包线划分方法 1.1 间隙度量
令K为Hilbert空间中的线性算子:
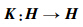
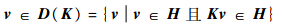
定义1 Hilbert空间内两个闭合算子K1和K2的间隙定义为
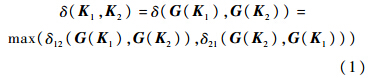
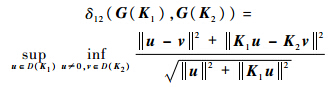
当飞行器处于不同状态点时,高度H、马赫数Ma均存在不同程度的差异,进而造成稳定状态点的小偏离线性化模型的差异,即线性空间模型可表示为高度、马赫数的函数:
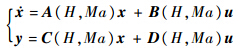
其传递函数为P(s)=C(sI-A)－1B+D,I为单位阵.显然P(s)是Hilbert空间中的线性算子.若P1和P2为两系统的传递函数,则这两个系统之间的间隙可以利用算子的间隙表示为
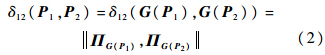
定义2 假设P∈Rn×m(s),并且有(M,N)与(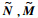
)分别为被控对象P的左右互质分解,则有正交投影矩阵为
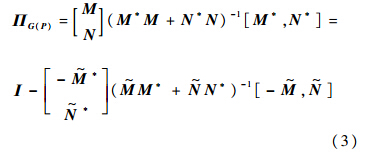
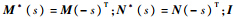为单位阵.P的左右互质分解形式如式(4)所示:
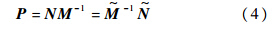
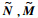∈H,且满足
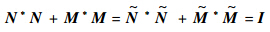
互质分解方法描述如下:
1) 求传递函数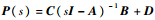
,其中(A,B)稳定,(A,C)可观;
2) 求取矩阵F和H,使得AF=A+BF,AH=A+HC稳定,并令
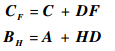
3) 互质分解形式为
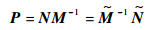
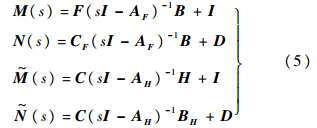
则线性系统的间隙度量可由式(6)和式(7)计算得出.
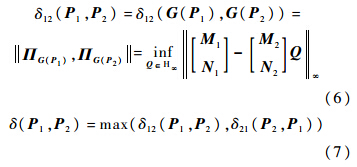
由间隙度量的定义,如果δ接近于0,则表明两个系统动态特性近似;相反,δ越接近于1,则表明两系统的动态特性差别越大[11,12].间隙度量计算的是两个系统空间差异,并不要求两个系统有相同的正极点数.如果两个开环系统(可能不稳定)的间隙度量值很小,则其对应的闭环系统也近似.因此,间隙度量值的大小可反映模型变化的大小,依此可作为包线划分的依据. 1.3 包线划分步骤
将飞行包线记为Ψ,最终要将Ψ划分为n个子区域,每个子区域记为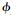
j,相应地每个子区域均有一个间隙度量极小点(即标称点),该状态点与子区域内其余状态点模型特性差异最小,记为Ej,其中j=1,2,…,n.
针对第j个子区域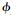j,该子区域高度范围记为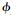Hj,表示该子区域高度变化区间为[Hjmin,Hjmax];同样地,该子区域马赫数范围记为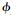Maj,表示该子区域马赫数变化区间为[Majmin,Majmax].
对于子区域任意两个状态点(不同H或Ma),记为Ea1,Ea2,其对应的线性模型为Pa1,Pa2,其间隙度量值记为δ(Ea1,Ea2),则间隙度量极小点Ej需满足
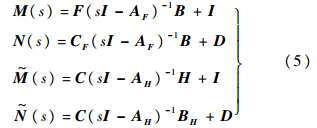
此外,包线划分时,在保证子区域涵盖整个包线的前提下,要尽量减少子区域的个数,即
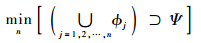
综上所述,飞行包线标称点Ej的选择需满足如下优化条件:
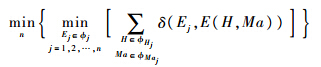
为实现上述优化,如图 1所示,采取以下3个步骤.
 |
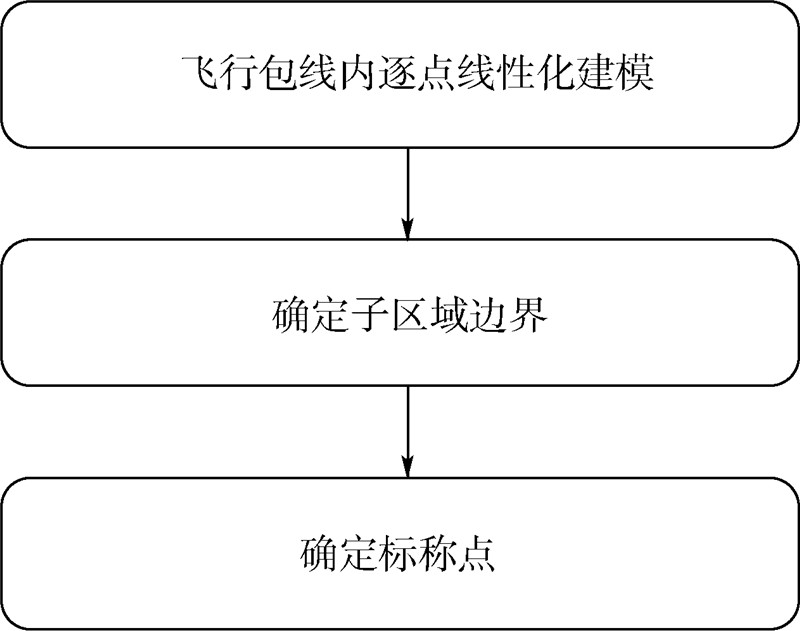| 图 1 基于间隙度量的包线划分方法流程图 Fig. 1 Flowchart of envelope division method based on gap metric |
1) 在飞行包线内建立一系列线性化模型,作为分析模型特性变化规律的基础.
将飞行包线内按照一定间隔ΔH,ΔMa网格化,则共有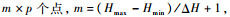
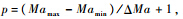并配平线性化从而得到一系列线性模型.
理论上间隔ΔH,ΔMa选取越小,越能精确分析相邻状态点的模型特性差异,越能找出模型特性的变化规律,但计算量会相应增加.
2) 计算相邻状态点模型之间的间隙度量值,并对其进行分析,以确定区域边界.
分别计算包线内每个状态点E(H,Ma)随高度和马赫数的间隙度量变化率,即取同一高度H0(或马赫数Ma0)下间隙度量随马赫数(或高度)的变化率,即可表示为
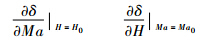
已知如果两个模型的间隙度量值δ越小,则表明两个模型动态特性越相近;相反,δ越大(≤1),则表明两模型的动态特性差别越大.当δ足够大时,一个控制器同时适应两个模型特性就会显得困难,因此可定义一个基于间隙度量的指标γ来表示该界限.
即当间隙度量值累积到γ时:
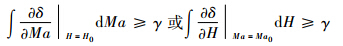
则对应的高度或马赫数即作为分区边界,其中γ值的选取应根据实际对象特性确定.
3) 一般情况下,一个飞行区域内的标称点要满足与区域内其他状态点的模型特性差异最小,在以间隙度量为衡量指标情况下,确定标称点即为寻找子区域的“间隙度量极小点”.
即求得状态点Ea0,使其与子区域内其余状态点Eb间隙度量值的均值达到最小,即满足
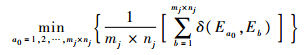
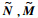j的网格数，j=1,2,…,n.2 包线划分举例验证
针对某型高超声速飞行器,以高度范围[10,34]km,马赫数范围[1,10]为例.将飞行包线内的状态点按照一定间隔(ΔH=2km,ΔMa=1)进行线性化,得到一系列线性模型.
依据上述所提方法,分别计算得到固定高度或固定马赫数下间隙度量变化率,即
 |
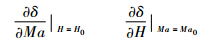
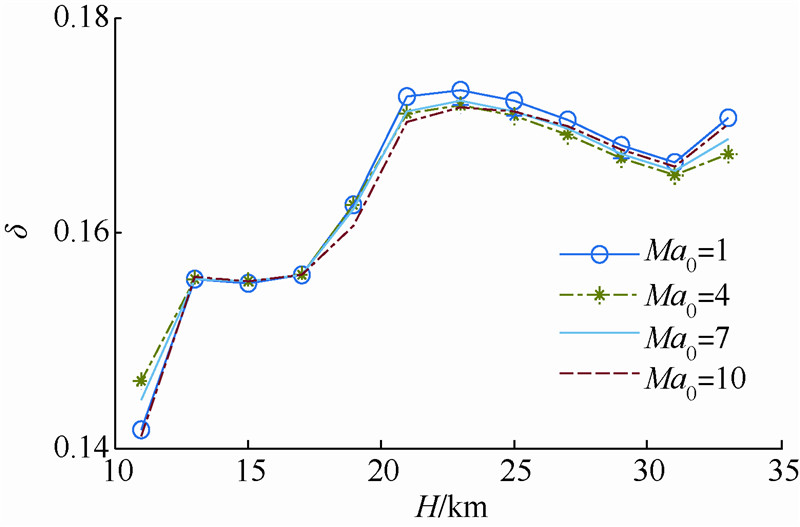| 图 2 同一马赫数下间隙度量随高度变化率 Fig. 2 Changing curves of gap metric with height at same mach |
 |
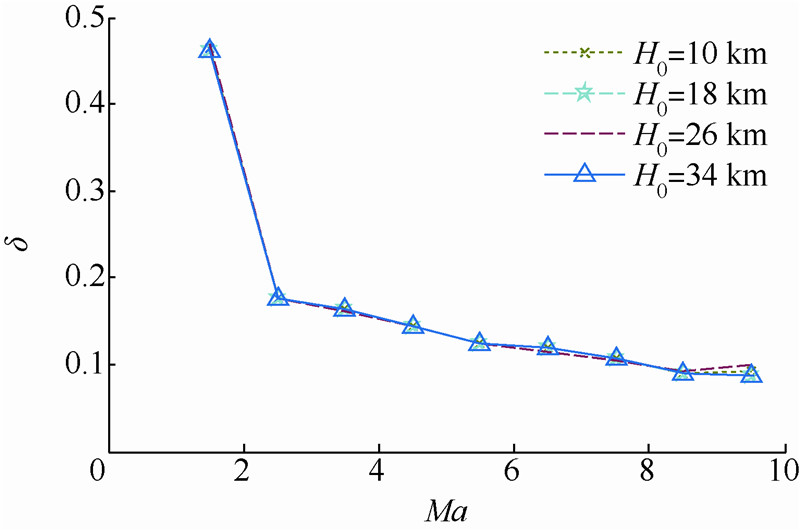| 图 3 同一高度下间隙度量随马赫数变化率 Fig. 3 Changing curves of gap metric with Mach at same height |
研究显示,本对象模型的间隙度量值变化累计超过0.8时,就难以用一个控制器实现控制,故取γ=0.75.
如图 2所示,当马赫数固定时,在[10,34]km高度范围内可划分为3个子区间,即[10,18]km,[18,26]km,[26,34]km.如图 3所示,当高度固定时,在[1,10]马赫数范围内可划分为2个子区间,即[1,4],[4,10].包线划分结果如图 4所示.
 |
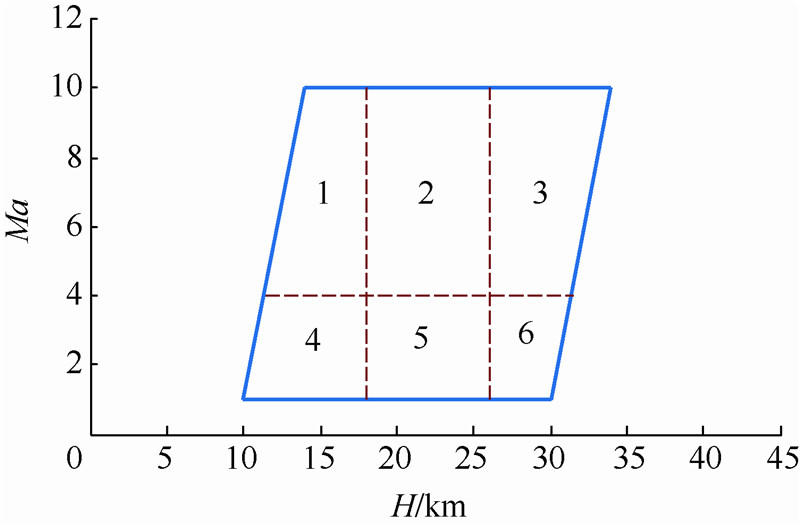| 图 4 包线划分结果示意图 Fig. 4 Flight envelope division result |
以图 4中区域2为例,分别计算各个状态点与其余状态点模型间隙度量值,取均值如图 5所示.可知点Ea0(H=24km,Ma=9)与其余状态点处模型间隙度量值最小,说明点Ea0处的模型特性与子区域内其余点差异最小,即可取间隙度量极小点Ea0作为该子区域的标称点.
 |
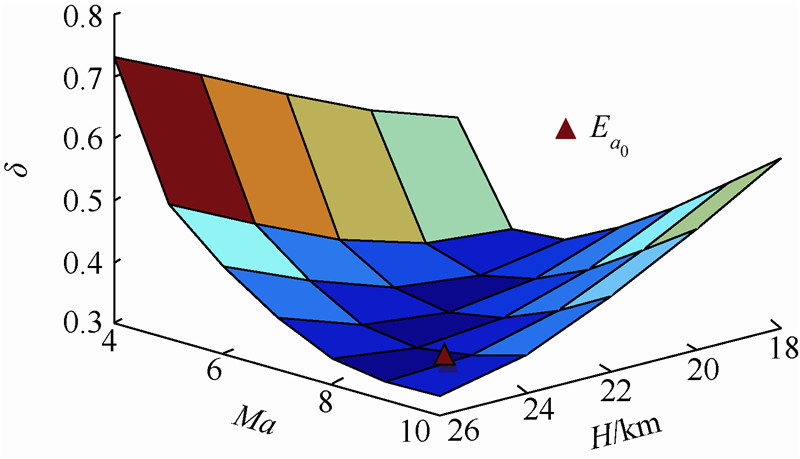| 图 5 间隙度量极小点示意图 Fig. 5 Schematic of gap metric minimum point |
为验证间隙度量极小点选取的合理性,比较Ea0点与分区内其余状态点的各个通道的频率特性,如图 6~图 8所示,Ea0状态点线性模型的Bode图处在整个区域内其他状态点的Bode图分布包络的正中心处,表明了间隙度量极小点选取的合理性.基于该状态点的线性模型所设计的控制器在区域内其余状态点工作时,往往能够表现出更优异的性能.
 |
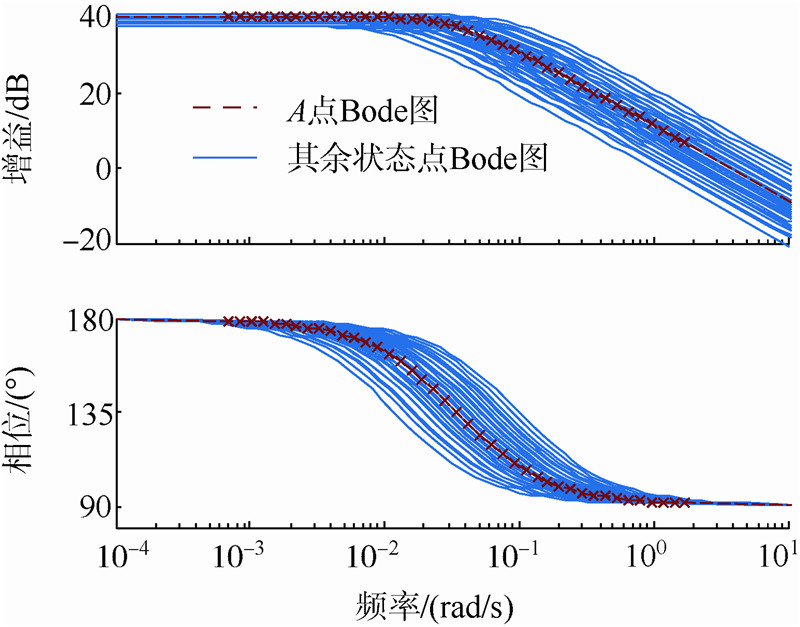| 图 6 Ea0点与其余状态点频域特性对比(滚转通道) Fig. 6 Comparison chart of frequency-domain charact- eristics between Ea0 and other state point (roll channel) |
 |
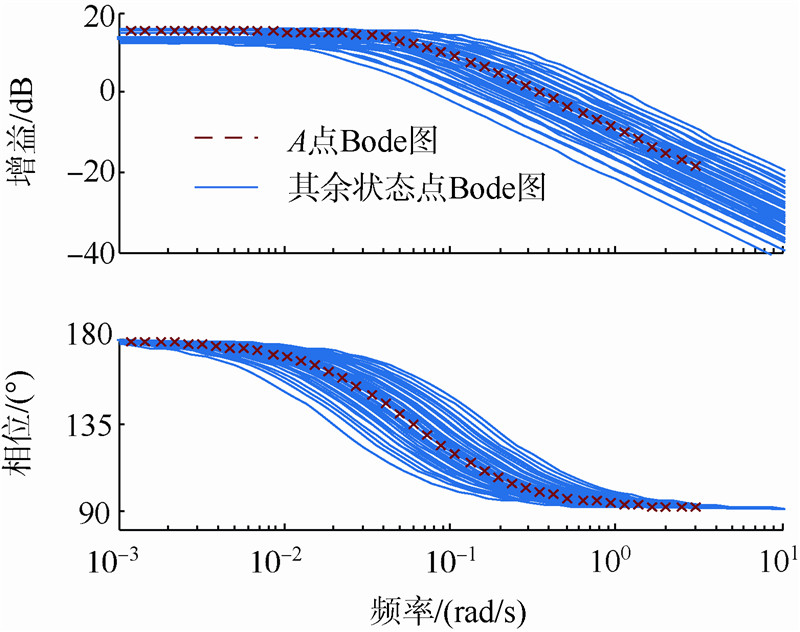| 图 7 Ea0点与其余状态点频域特性对比(偏航通道) Fig. 7 Comparison chart of frequency-domain charact- eristics between Ea0 and other state point (yaw channel) |
 |
| 图 8 Ea0点与其余状态点频域特性对比(俯仰通道) Fig. 8 Comparison chart of frequency-domain charact- eristics between Ea0 and other state point (pitch channel) |
为验证分区结果的有效性,采用极点配置方法针对间隙度量极小点设计控制器,并验证同一控制器能否覆盖子区域内其余状态点.三轴姿态角同时加阶跃指令,仿真结果如图 9、图 10所示.
 |
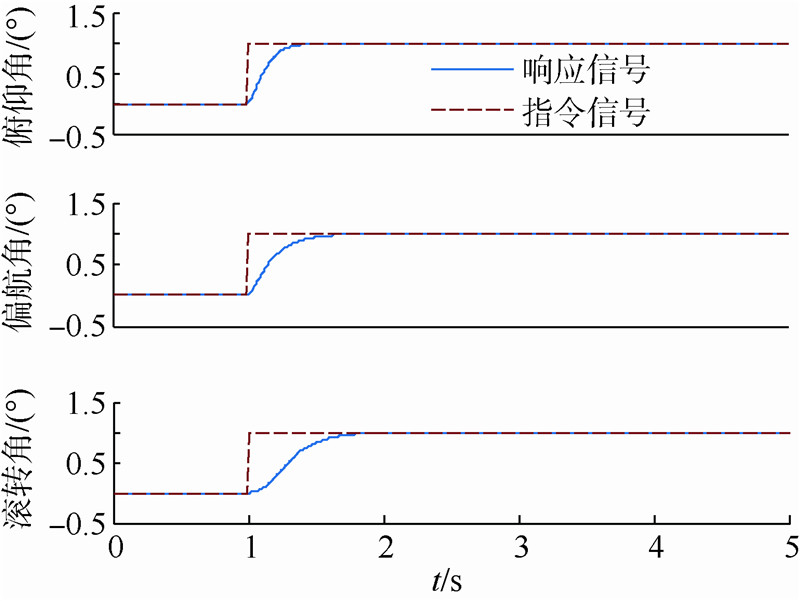| 图 9 间隙度量极小点Ea0阶跃响应曲线 Fig. 9 Response curves for the state of gap metric minimum point Ea0 |
|
| 图 10 子区域内所有网格点阶跃响应曲线 Fig. 10 Response curves for all states within the subrange |
如图 10所示,在基于标称点所设计的控制器下,按照一定间隔,对覆盖整个子区域的各个状态点(共5×7个)进行仿真分析.仿真结果表明,基于标称点A设计的控制器能够覆盖子区域内所有状态点,从而反映了区域划分的合理性.
3 结 论
1) 间隙度量理论能够为包线划分提供依据，通过实例验证，结果表明基于间隙度量的包线定量划分方法能够实现飞行包线的合理划分；
2) 相较于传统划分方法，基于间隙度量的划分方法能够大幅降低包线划分的工作量，故更具有工程实用性.
| [1] | 李中建.大包线飞行控制系统鲁棒设计研究[D].西安:西北工业大学,2000 Li Zhongjian.Research on large envelope flight robust control system[D].Xi’an:Northwesten Polytechnical University,2000(in Chinese) |
| Cited By in Cnki (22) | |
| [2] | 陶涛.航空发动机鲁棒控制研究[D].西安:西北工业大学,1997 Tao Tao.Robust control of aeroengine[D].Xi’an:Northwesten Polytechnical University,1997(in Chinese) |
| Cited By in Cnki | |
| [3] | 王进,李剑,谢寿生.航空发动机控制问题研究中飞行包线区域的划分方法[J].航空动力学报,2003,18(2):436-439 Wang Jin,Li Jian,Xie Shousheng.Flight envelope division method in aeroengine control study[J].Journal of Aerospace Power,2003,18(2):436-439(in Chinese) |
| Cited By in Cnki (8) | |
| [4] | 王海泉,郭迎清,李睿,等.航空发动机全飞行包线鲁棒控制器设计研究[J].测控技术,2009,28(5):48-51 Wang Haiquan,Guo Yingqing,Li Rui,et al.Design of full flight envelope controller for aeroengine[J].Measurement & Control Technology,2009,28(5):48-51(in Chinese) |
| Cited By in Cnki (5) | |
| [5] | 李述清,张胜修,胡卫红.用于控制器分区设计的发动机飞行包线区域最优划分[J].航空动力学报,2012,27(2):445-449 Li Shuqing,Zhang Shengxiu,Hu Weihong.Partion optimization in the flight envelope for control design of aero-engines[J].Journal of Aerospace Power,2012,27(2):445-449(in Chinese) |
| Cited By in Cnki (1) | |
| [6] | 杨大鹏.某无人机全包线控制律设计技术研究[D].南京:南京航空航天大学,2012 Yang Dapeng.Research on control technologies over full flight envelope for UAV[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2012(in Chinese) |
| Cited By in Cnki | |
| [7] | 曾丽兰.基于H∞回路成形的无人直升机非脆弱鲁棒飞行控制研究[D].南京:南京航空航天大学,2006 Zeng Lilan.Unmanned helicopter non-fragile robust flight control research based on H∞ loop shaping[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2006(in Chinese) |
| Cited By in Cnki (5) | |
| [8] | 刘斌,王常虹,李伟.间隙度量与跟踪系统中的鲁棒控制器设计[J].控制与决策,2010,25(11):1714-1718 Liu Bin,Wang Changhong,Li Wei.Gap metric and robust controller design in tracking systems[J].Control and Decision,2010,25(11):1714-1718(in Chinese) |
| Cited By in Cnki (3) | |
| [9] | El-Sakkary A K.The gap metric:robustness of stabilization of feedback systems[J].IEEE Transactions on Automatic Control,1985,30(3):240-247 |
| Click to display the text | |
| [10] | Zames G,El-Sakkary A K.Unstable systems and feedback:the gap metric[C]//Proceedings of Allerton Confon Communication,Control,and Computing.Urbana:University of Illinois at Urbana-Champaign,1980:380-385 |
| [11] | Georgiou T T.On the computation of the gap metric[J].Systems and Control Letters,1988,11(4):253-257 |
| Click to display the text | |
| [12] | Georgiou T T,Malcolm C S.Robust stabilization in the gap metric:controller design for distributed plants[J].IEEE Transactions on Automatic Control,1992,31(8):1133-1139 |
| Click to display the text | |
| [13] | Cantoni M.A characterisation of the gap metric for approximation problems[C]//Proceedings of the 45th IEEE Conference on Decision and Control.Piscataway,NJ:IEEE,2006:5359-5364 |
| [14] | French M.Adaptive control and robustness in the gap metric[J].IEEE Transactions on Automatic Control,2008,53(2):461-478 |
| Click to display the text | |
| [15] | Galan O,Romagnoli J A,Arkun Y,et al.On the use of gap metric for model selection in multi-linear model-based control[C]//Proceedings of the American Control Conference. Piscataway,NJ:IEEE,2000,6:3742-3746 |
