表1(Table 1)
2003年,美国DARPA与空军联合启动了FALCON计划,该计划的近期目标是使用小型运载火箭将通用航空飞行器(CAV)或增强型CAV(ECAV)发射到亚轨道,然后CAV再入机动滑翔飞行实现快速打击[1].CAV飞行环境复杂,受到各种干扰和约束条件的限制,对其再入轨迹优化研究一直以来都是许多学者研究的热点[2, 3, 4].再入初值受到外界干扰会直接影响再入轨迹的生成,此外滑翔段气动参数摄动也会使得飞行器有可能不满足原本狭窄的再入走廊要求.因此,研究具有随机干扰问题的高超声速滑翔飞行器轨迹优化问题显得尤为必要.
高超声速滑翔飞行器动力学方程复杂,其轨迹优化是非线性最优控制问题,很难获得解析解,当系统中含有不确定性元素时,数值方法有可能就是唯一的方法.
最常用的随机问题数值方法为蒙特卡洛(MC,Monte Carlo)方法,它通过对服从已知概率密度函数的随机变量进行采样,并且将采样值加入到状态方程中,然后求解确定性问题.虽然MC方法对于不确定问题求解有效,但是MC方法的收敛速度缓慢,特别是具有多个随机变量时计算负担较大.文献[5, 6]应用MC方法对再入飞行器预测校正制导律进行了仿真,验证了制导方法的鲁棒性.
近年来,广义正交多项式(gPC,generalized Poly-nomial Chaos)方法在数值求解不确定问题方面具有广泛的应用[7, 8, 9, 10].它是一种随机空间的特殊表达方式,它将随机不确定性解转化为以随机变量作为输入参数的正交多项式,具有较快的收敛速度.
本文针对干扰服从正态随机分布的高超声速滑翔式飞行器再入轨迹优化问题,建立了运动学模型、气动参数拟合模型和各种约束模型.基于gPC方法提出了具有随机干扰的轨迹优化数值解法,以最大纵程为代价函数针对干扰初值和气动干扰分别进行了数字仿真,证明了此方法的有效性.通过与MC方法的比较得知,基于gPC方法的轨迹优化方法比MC方法具有更高的计算精度,计算效率方面也明显优于MC方法. 1 轨迹优化模型 1.1 运动学模型
考虑地球自转的影响,建立高超声速滑翔再入无量纲运动方程：
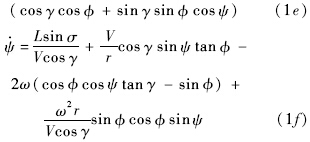
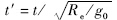的导数;r,θ,φ,V,γ,ψ分别为无量纲化的地心距、经度、纬度、地球相对速度、弹道倾角和弹道偏角;使用上标R代表有量纲化状态,状态量无量纲化关系为r=rR/Re,V=VR/
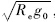,L=LR/mg0,D=DR/mg0,g=g0(Re/R)2,ω=ωR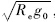;σ为倾侧角;rR为地心距;Re为地球平均半径;m为飞行器质量;ωR为地球自转角速度;LR为升力;DR为阻力;g0为海平面重力加速度.
1.2 气动参数拟合模型
在高超声速飞行条件下,气动力系数近似满足抛物线阻力极线关系,且在马赫数较大时,可近似认为气动力系数为攻角的线性函数[11].参考文献[12]中给出的CAV-H的气动参数表格,对升力系数CL和阻力系数CD进行插值拟合,可以得到
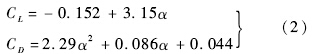
升力和阻力的计算公式为
高超声速滑翔式飞行器从大气层外的预定高度再入,在飞行过程中主要受到以下约束条件:
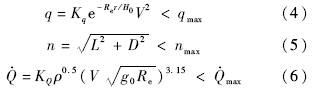
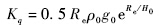
此外,为了满足末制导交班的需要,飞行器在滑翔段终端要满足约束:
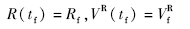
建立带初始随机干扰和状态随机干扰的最优控制问题如式(7)所示.
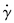;p=[p1,p2,…,pNp]为随机变量,Np为随机变量的个数,各随机变量之间相互独立.为了对结果进行估计,建立观测方程z=Gc(X).Gc(X)为观测矩阵,其元素可以包括状态值、代价和时间等. 2.2 随机轨迹优化问题求解方法
随机轨迹优化问题的一般性解法如图 1所示.
 |
| 图 1 随机轨迹优化解法Fig. 1 Solution of stochastic trajectory optimization |
首先对随机变量进行采样处理,将每个采样值代入确定性最优控制问题进行求解,形成解空间,最后对观测值进行估计,计算统计特性输出. 3 随机变量处理 3.1 基本定义
定义概率空间为(Ω,A,P),Ω表示样本空间,A为样本空间中的可能性事件,P为可能性事件概率.假设ρi,i=1,2,…,Np为随机变量pi(w),w∈Ω 的概率密度函数,由于随机变量之间相互独立,则联合概率密度为式(8)所示.
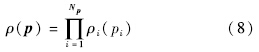
设Γi≡pi(Ω),将概率密度函数转换到样本空间Ω的有限范围(例如正态分布为3σ区域)内,则总的有限范围定义为
gPC使用多维正交多项式来近似随机变量p,而一维正交多项式空间扩展到多维空间成为维数扩展关键[13].一维多项式空间定义为
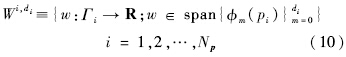
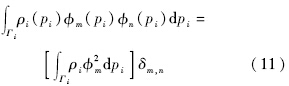
则Np个一维正交多项式的基张成了多维正交多项式空间,记为
其中,P为正交多项式空间的总阶数,有
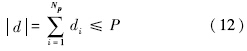
扩维后的正交多项式也必须满足正交性条件：
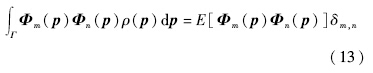
确定性最优控制问题的数值解法可以分为直接法和间接法.直接法无需求解最优必要性条件,而是将连续最优控制问题离散并参数化,直接应用求解非线性规划的方法对性能指标寻优,本文采用直接法进行求解. 4.1 时间区间转换
将时间区间[t0,tf]划分为K份区间t∈[tk－1,tk],k=1,2,…,K,tk－1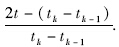
设Xk(τ)和Uk(τ)为第k个区间上的状态和控制变量,则连续时间Bolza问题转化为以下形式:
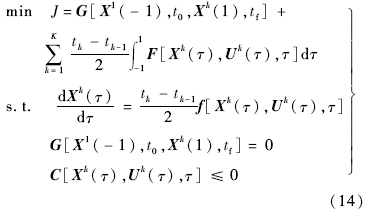
需要指出的是X1(－1)为叠加随机变量采样的状态初值. 4.2 轨迹优化问题离散化
轨迹优化问题离散化是在一定的节点上使用相应的插值多项式对状态方程、约束方程和代价函数的离散化[14].目前可以使用的节点主要有CG(Chebyshev-Gauss),CGL(Chebyshev-Gauss-Lobatto),LGL(Legendre-Gauss-Lobatto),LG(Legendre-Gauss)和LGR(Legendre-Gauss-Radau).
除CGL配点法外,其他配点法都满足协态映射准则[15],本文选用LGR配点法进行离散化.
1) 状态方程离散化.通过对全局插值多项式求导来近似状态变量对时间的导数,从而将微分方程约束转换为一组代数约束.
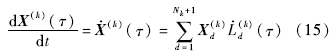
为Lagrange多项式的基,
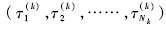为在第k个网格时间区间的节点,Nk为第k个网格区间中节点数.将式(15)代入式(14)中的动力学微分方程中,并在节点上进行离散,可得
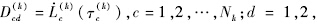…,Nk+1;D(k)(c，d)=Dcd(k);Dk为第k个网格区间处的伪谱微分矩阵.2) 约束条件的离散化.路径约束条件C[X(t),U(t),t]在Nk个配置点处离散化方程为
3) 目标函数的离散化.目标函数的离散化是利用Lagrange积分代替目标函数的积分项.离散化结果为
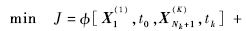
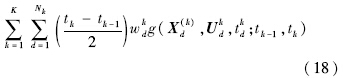
至此,式(15)~式(18)将最优控制问题转化为非线性规划问题,可以通过NLP求解器SNOPT软件进行求解,最后得出状态量、控制量的解集空间,形成观测值解空间. 5 观测值估计
当得到观测值解空间后,就可以多维正交多项式对观测值进行求解,观测方程的近似解为
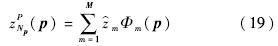
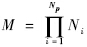,Ni为第i个随机变量选取的配点个数;
为扩展系数,表达式为
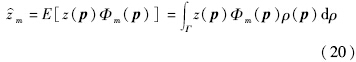
扩展系数的积分求解是一个关键点并且是一个难点.gPC方法基于积分准则选取一定的配点和权重,利用高斯积分方法对扩展系数中的积分求解.多项式的选择与随机分布有关,而配点和权重的选择又必须跟积分准则一致,例如,如果选取Hermite正交多项式的基来近似Gauss分布随机变量,那么必须选择Gauss-Hermite积分准则和Gauss-Hermite配点.表 1给出了高斯(Gauss)分布和均匀(Uniform)分布对应的正交多项式和配点类型.
| 随机分布 | 正交多项式 | 配点 |
| Gauss | Hermite | Gauss-Hermite |
| Uniform | Legendre | Legendre-Gauss |
选取一定的积分准则和配点及权重后,扩展系数近似表达式为
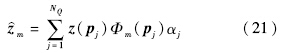
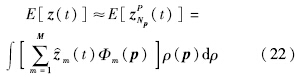
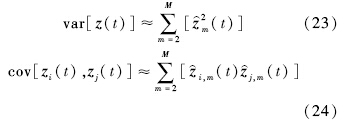
基于gPC方法的随机轨迹优化求解算法如图 2所示,具体步骤如下:
1) 根据随机变量的分布选择一定的配点和积分权重,并进行维数扩展.配点和积分权重的选取必须跟扩展系数中的积分准则相一致.
2) 利用生成的NQ个配点作为采样点,选取第Nq(q=1,2,…,Q)个配点代入到状态方程或初始条件中.
3) 对状态方程、约束方程和目标函数进行离散化,离散化为非线性规划问题,利用SNOPT软件进行求解,解出状态变量、控制变量、目标函数.Nq=Nq+1,如果Nq
4) 建立观测矩阵z=[X(t),U(t),J(X,U)]T.
5) 利用式(20)求解gPC扩展系数,并利用式(18)计算观测值估计值.
6) 利用式(21)~式(23)求解观测值的期望、方差和协方差.
 |
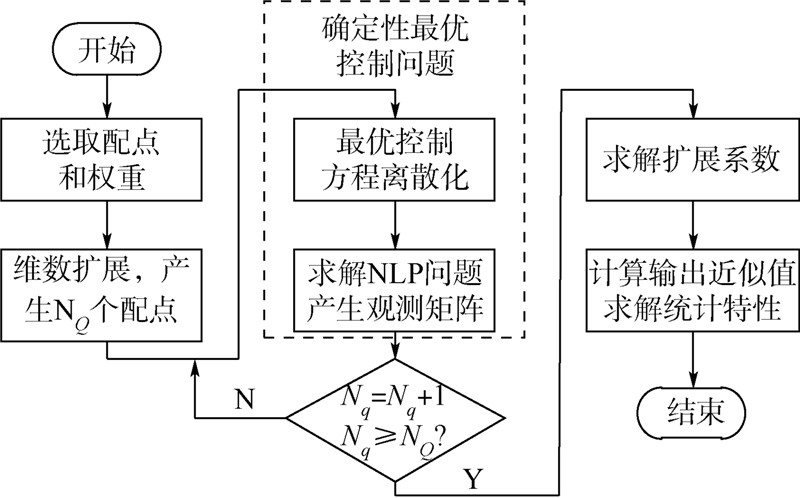| 图 2 随机轨迹优化求解流程Fig. 2 Solution chart of stochastic trajectory optimization |
给定初始位置(0°,0°),初始高度60km,初始速度6000m/s,初始弹道倾角－1°,初始弹道偏角90°.终端约束Rf=25km,VfR=2.4km/s;路径约束qmax=200kPa,nmax=6,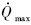
=2000kW/m2.以最大纵程J=maxθf作为代价函数对具有干扰初值和气动干扰的高超声速滑翔式飞行器的再入轨迹优化问题分别进行数字仿真,并与MC方法进行比较.
计算硬件平台CPU为1.8GHz/PentinuⅣ,操作系统为Windows XP,软件平台为Matlab R2011a. 7.1 考虑初始偏差的仿真
考虑初始纵向状态量高度h0、速度V0R和弹道倾角γ0服从正态分布,即[h0,V0R,γ0]~N(μ0,σ02),其中μ0和σ0分别为均值和标准差,μ0=[60km,
gPC方法选取随机变量的配点数目N1=N2=N3=7.MC方法取随机采样点300个.
仿真结果如图 3~图 15所示,使用gPC代表gPC方法,MC代表MC方法,de代表确定性轨迹优化方法.图 3为高度、速度和弹道倾角随机干扰的采样配点分布;图 4为速度-高度曲线;图 5为经度-纬度曲线,图 6显示了两种方法的落点图;图 7~图 9分别为弹道倾角曲线、弹道偏角曲线和控制量曲线;解空间中偏离估计轨迹的最大偏差沿均值轨迹对称画出棒形图,其中最大偏差ei=max(Xi)－zi,i=1,2,…,6,Xi为第i个状态的解空间.图 10~图 15为状态量的均方差(SD,Standard Deviation)曲线.由于不关心飞行时间,将时间映射到τ=[－1,1]上给出状态量曲线.
 |
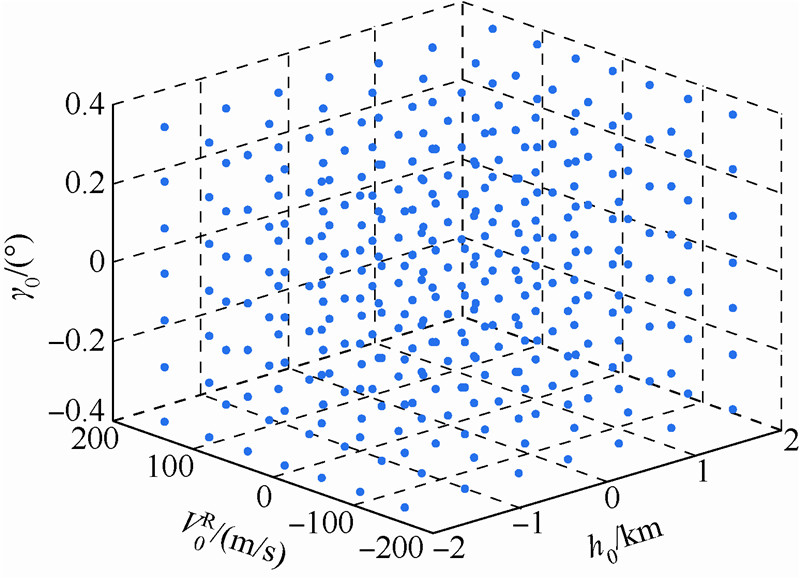| 图 3 随机变量初值采样配点Fig. 3 Samples of stochastic initial variables |
 |
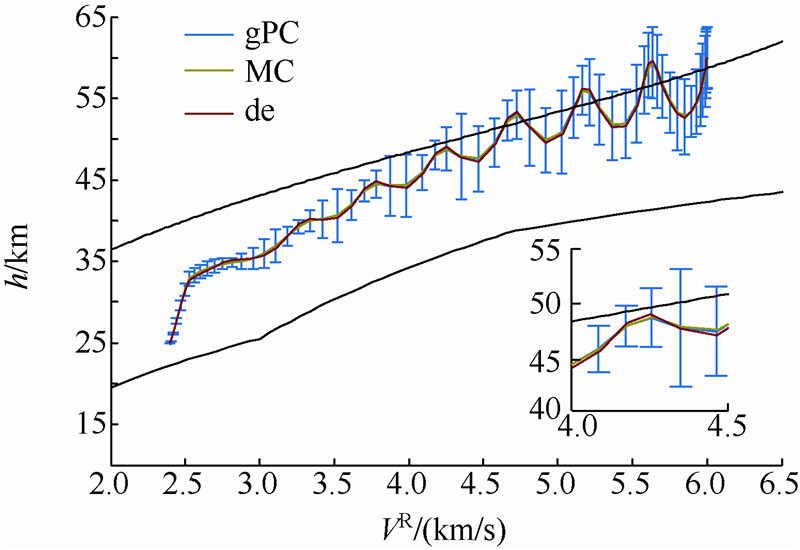| 图 4 初始偏差下的速度-高度曲线Fig. 4 Curves of velocity vs height under initial disturbance |
 |
| 图 5 初始偏差下经度-纬度曲线Fig. 5 Curves of longitude vs latitude under initial disturbance |
 |
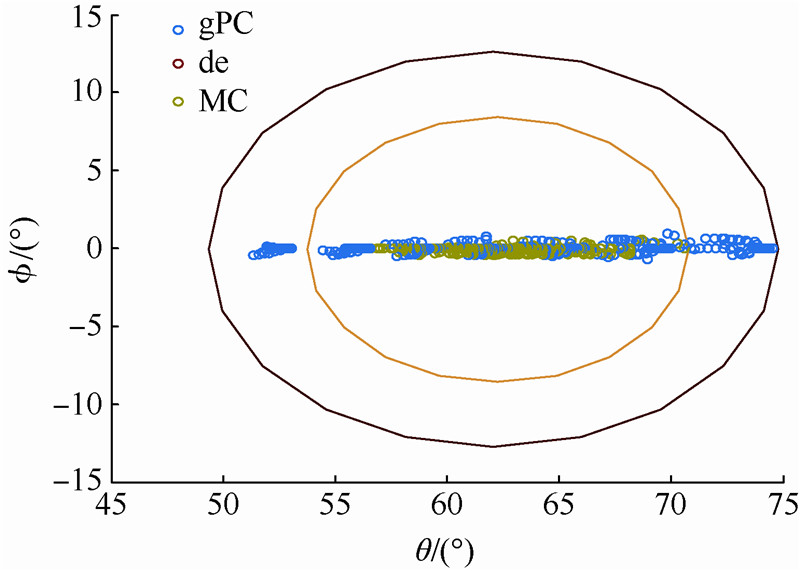| 图 6 初始偏差下的落点Fig. 6 Terminal positions under initial disturbance |
 |
| 图 7 初始偏差下的弹道倾角曲线Fig. 7 Curves of flight-path angle under initial disturbance |
 |
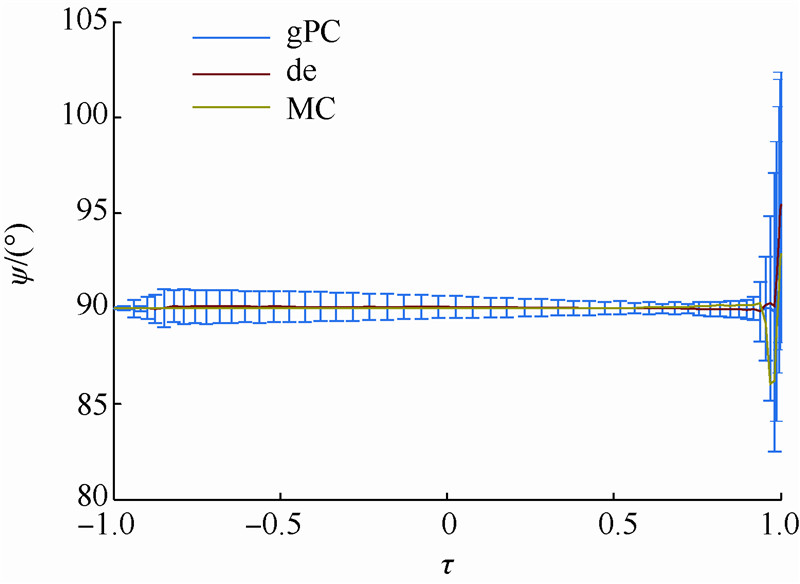| 图 8 初始偏差下的弹道偏角曲线Fig. 8 Curves of heading angle under initial disturbance |
 |
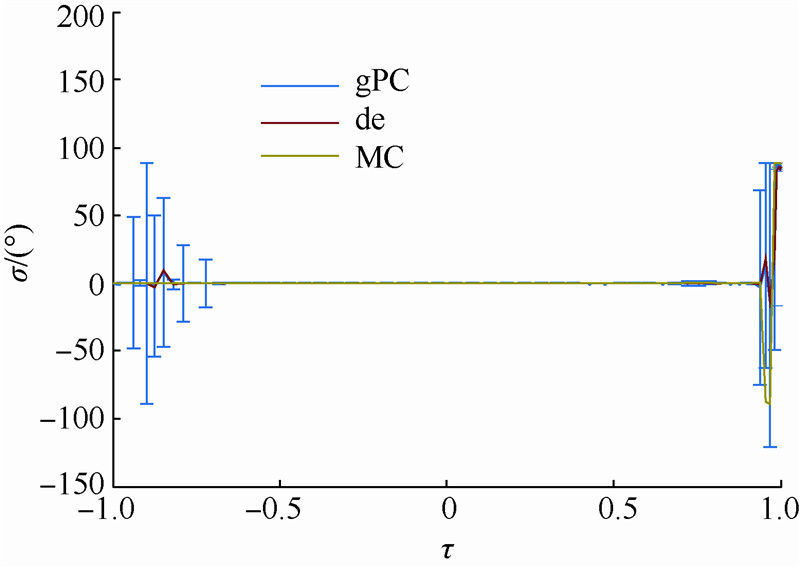| 图 9 初始偏差下控制量曲线Fig. 9 Curves of control under initial disturbance |
 |
| 图 10 初始偏差下的高度均方差曲线Fig. 10 SD curve of height under initial disturbance |
 |
| 图 11 初始偏差下的经度均方差曲线Fig. 11 SD curve of longitude under initial disturbance |
 |
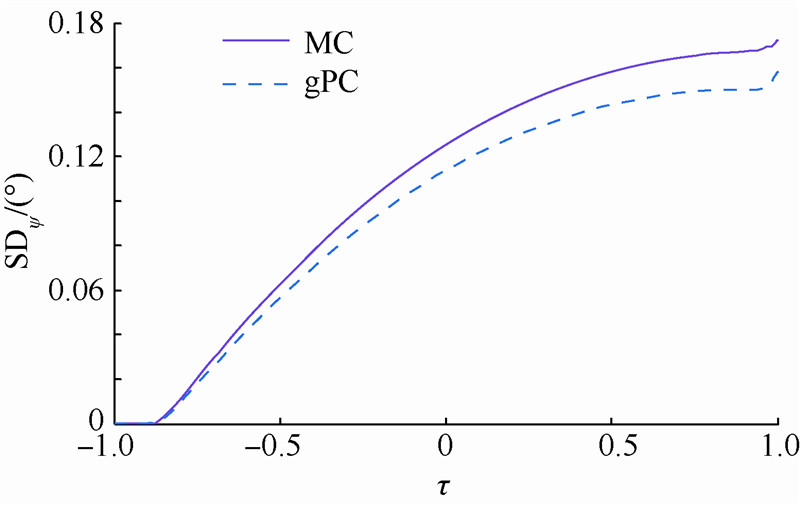| 图 12 初始偏差下的纬度均方差曲线Fig. 12 SD curve of latitude under initial disturbance |
 |
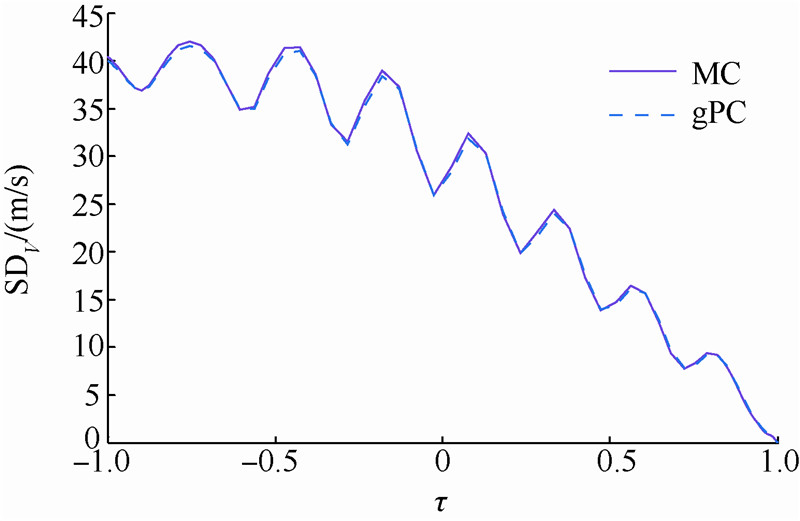| 图 13 初始偏差下的速度均方差曲线Fig. 13 SD curve of velocity under initial disturbance |
 |
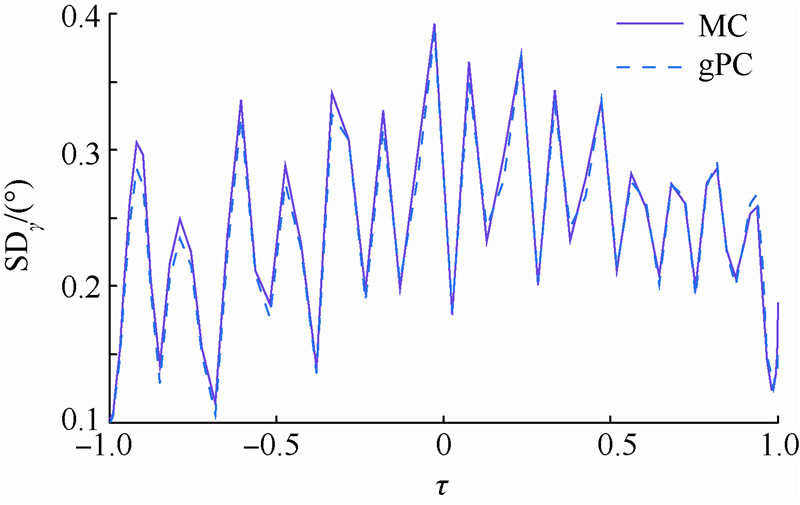| 图 14 初始偏差下的弹道倾角均方差曲线Fig. 14 SD curve of flight-path angle under initial disturbance |
 |
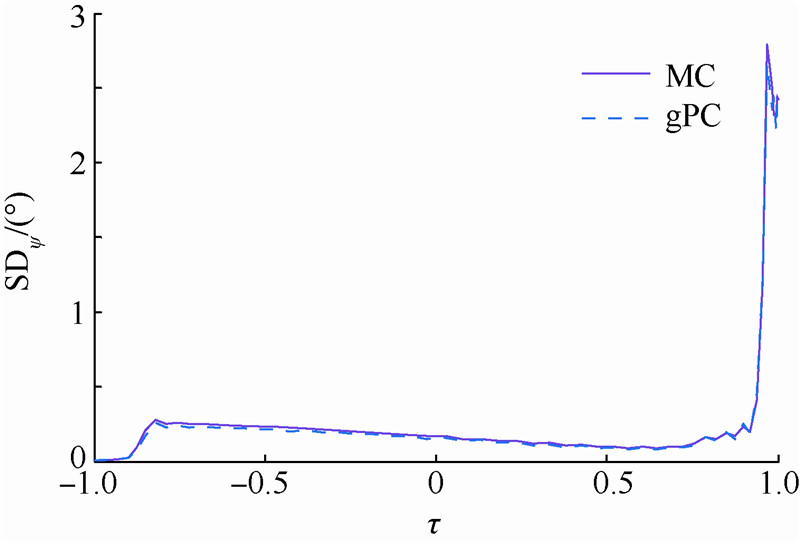| 图 15 初始偏差下的弹道偏角均方差曲线Fig. 15 SD curve of heading angle under initial disturbance |
可得出如下结论:
1) 由图 3可知,由于gPC方法随机变量配点数为7,随机变量的个数为3,总的配点数目Q=73=343.其中初始高度范围为[64, 56]km,初始速度范围为[5.6,6.4]km/s,初始弹道倾角的范围为[－1.4°,－0.6°],它们的所有组合构成了初始随机变量采样空间.
2) 由图 4速度-高度曲线可以看出,不同的再入初值对再入轨迹产生了一定的影响,在轨迹初期超出了再入走廊的上界(软约束),但是曲线不管怎么波动,始终没有超出再入走廊的下界(硬约束),满足过程约束条件;此外,在轨迹的末端,误差变得越来越小,最终达到了终端约束的高度和速度值.
3) 由图 4中的误差棒形图的计算公式(ei=max(Xi)-Zi,i=1,2,…,6)可知,它表征了轨迹的最大扩散范围,从图中可以看出,由于具有初始偏差,轨迹的扩散范围初始段最大,然后呈逐渐减小并收敛的趋势.
gPC与MC产生的期望轨迹与确定方法产生的轨迹基本一致,证明了gPC方法的有效性.
4) 图 5经度-纬度曲线可以看出,受初始值偏差的影响,曲线成发散趋势,由误差棒形图可以得到纬度最大扩散范围为±0.8°.gPC方法和MC方法得到的经度-纬度曲线与确定性轨迹方法得到的曲线基本上一致,但gPC方法更为接近.由于考虑了地球自转的影响,虽然是以最大经度为代价函数,但是纬度有一定的偏移.
5) 图 6中分别以gPC方法的期望落点为圆心,以gPC方法最大落点偏差为半径作圆;以MC方法的期望落点为圆心,以MC方法最大落点偏差为半径作圆.由图 6可以看出,具有随机初值干扰的最大纵程轨迹落点散布在赤道两侧,但偏差不大;虽然gPC方法初值干扰产生的落点散布比MC方法大,但是期望落点与确定性方法的落点更为接近.
6) 图 7显示弹道倾角在一定的范围内呈近似衰减振荡形式,使得飞行器轨迹跳跃下降,跳跃程度逐渐减小,末端为了达到终端约束值,弹道倾角增大,轨迹下压以满足终端高度和速度约束.
7) 由图 8和图 9可知,由于本文算例以最大经度为代价函数,所以弹道偏角近似保持在90°附近,控制量保持为零,也就使得飞行器沿着赤道飞行,达到最大经度.大部分时间内弹道偏角和控制量波动较小,只有在末端为了达到终端约束,出现了一定的波动.
8) 由图 10~图 15可以看出,均方差显示了状态量偏离期望值的程度,对于初始偏差,gPC方法较MC方法产生的状态量均方差略小.图 10和图 13显示高度和速度具有初始偏差,但均方差逐渐减小,证明了图 4中速度-高度散布逐渐减小的结果;同理,图 11和图 12显示经度和纬度的均方差逐渐增大,也证明了图 5经度-纬度曲线逐渐散布的结果.
9) 从计算时间上来说,基于gPC方法的随机轨迹优化方法消耗的时间在20min左右,基于MC方法消耗的时间却在1h以上,由此可以看出基于gPC方法的随机轨迹优化方法计算效率明显优于MC方法.但是两种方法都不能作为在线轨迹优化方法使用. 7.2 考虑气动偏差的仿真
考虑到气动参数是通过特定马赫数下进行插值拟合得到的,不可避免地存在着建模误差,本节考虑ρ0,CL和CD的随机干扰服从均值为零,方差分别为0.05,0.04和0.04的正态分布.同样选取随机变量的配点数目N1=N2=N3=7,MC方法取点300个.
仿真结果如图 16~图 28所示.
 |
| 图 16 气动干扰参数随机采样配点Fig. 16 Samples of stochastic perturbed variables |
 |
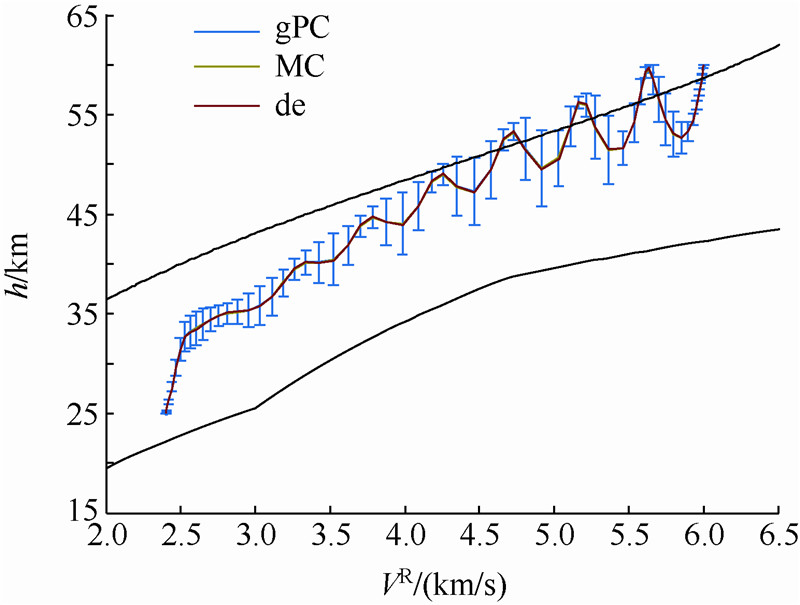| 图 17 气动干扰下的速度-高度曲线Fig. 17 Curves of velocity vs height under aerodynamic disturbance |
 |
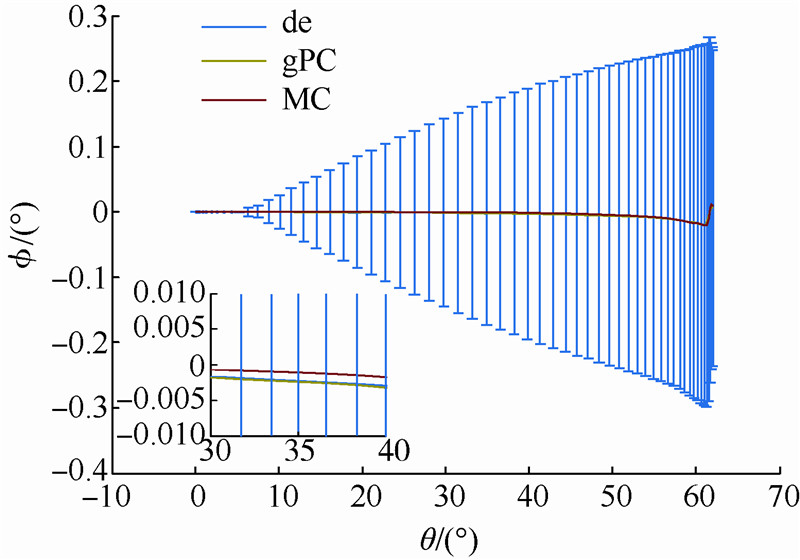| 图 18 气动干扰下的经度-纬度曲线Fig. 18 Curves of longitude vs latitude under aerodynamic disturbance |
 |
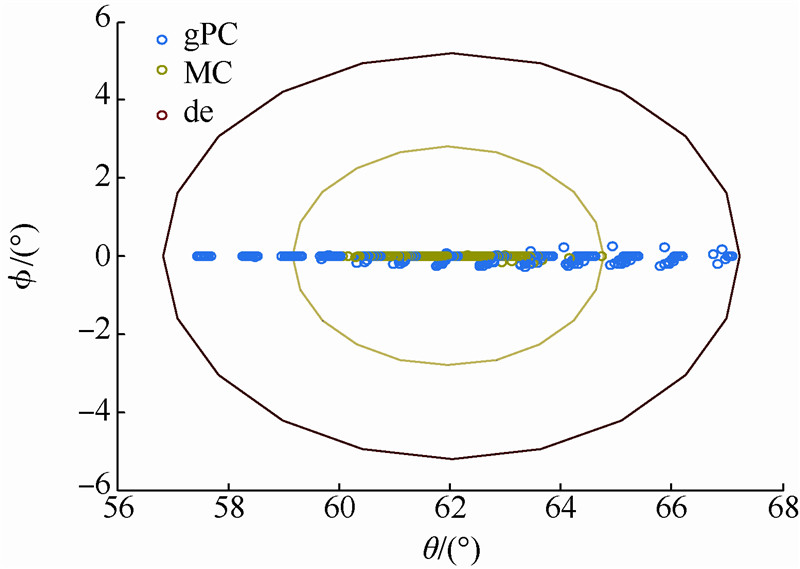| 图 19 气动干扰下的落点Fig. 19 Terminal positions under aerodynamic disturbance |
 |
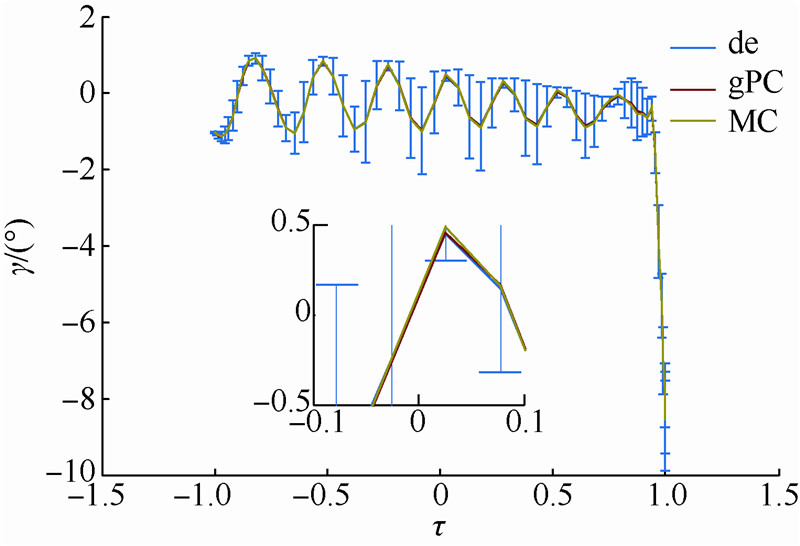| 图 20 气动干扰下的弹道倾角曲线Fig. 20 Curves of flight-path angle under aerodynamic disturbance |
 |
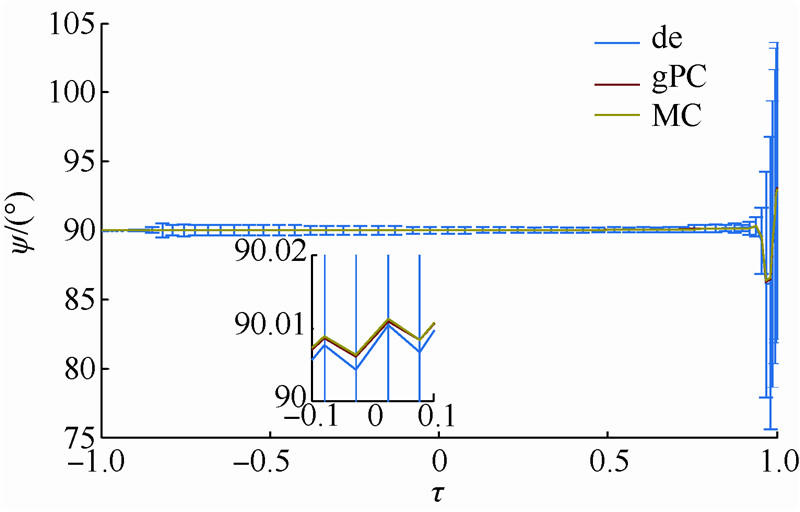| 图 21 气动干扰下的弹道偏角曲线Fig. 21 Curves of heading angle under aerodynamic disturbance |
 |
| 图 22 气动干扰下的控制量曲线Fig. 22 Curves of control under aerodynamic disturbance |
 |
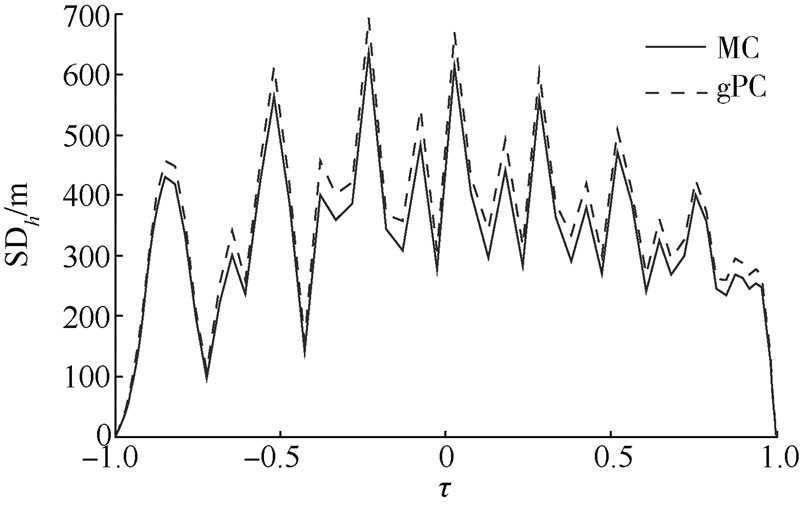| 图 23 气动干扰下的高度均方差曲线Fig. 23 SD curves of height under aerodynamic disturbance |
 |
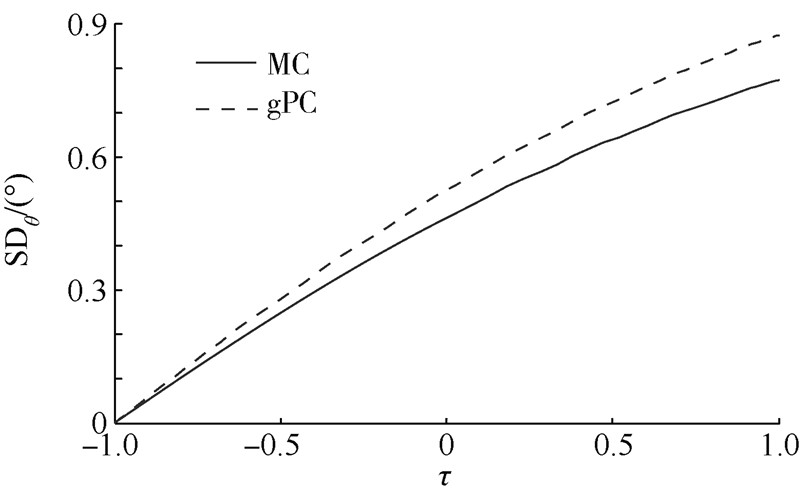| 图 24 气动干扰下的经度均方差曲线Fig. 24 SD curves of longitude under aerodynamic disturbance |
 |
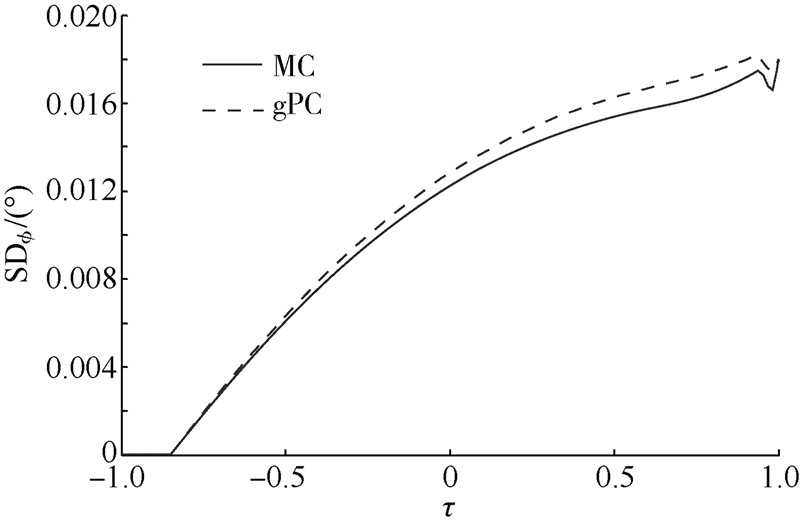| 图 25 气动干扰下的纬度均方差曲线图Fig. 25 SD curves of latitude under aerodynamic disturbance |
 |
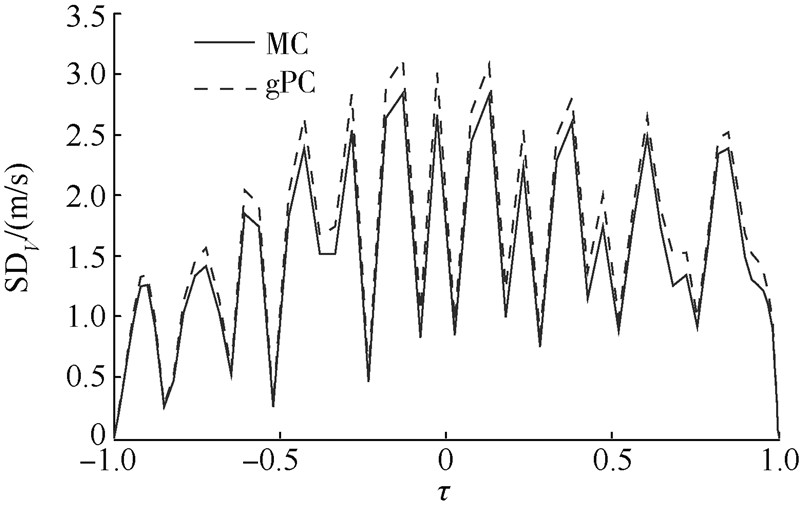| 图 26 气动干扰下的速度均方差曲线Fig. 26 SD curves of velocity under aerodynamic disturbance |
 |
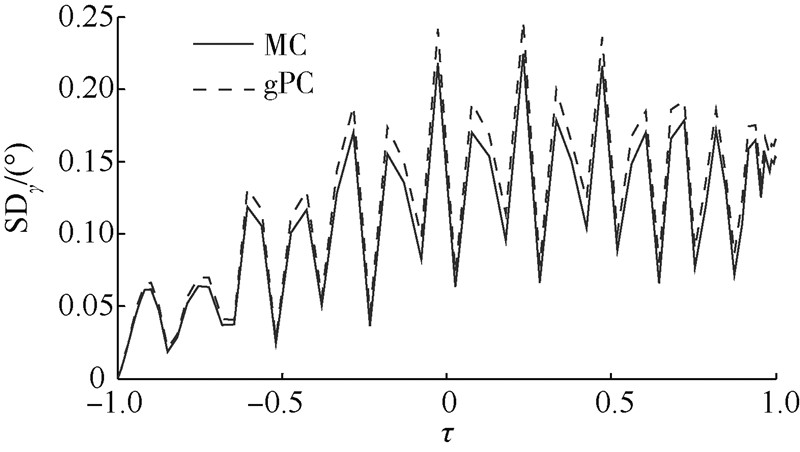| 图 27 气动干扰下的弹道倾角均方差曲线Fig. 27 SD curves of flight-path angle under aerodynamic disturbance |
 |
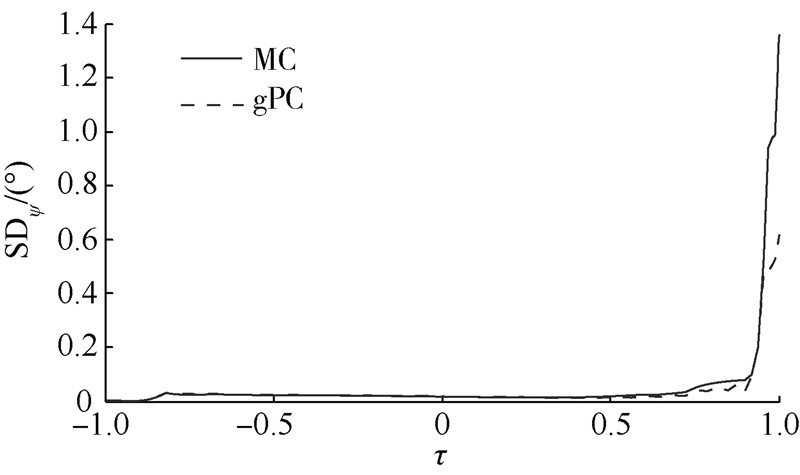| 图 28 气动干扰下的弹道偏角均方差曲线Fig. 28 SD curves of heading angle under aerodynamic disturbance |
可以得出如下结论:
1) 图 16显示了气动参数干扰值随机干扰p(ρ),p(CL)和p(CD)的采样范围,总共产生343个随机采样配点,其中p(ρ)∈[－0.2,0.2],p(CL)∈[－0.15,0.15],p(CL)∈[－0.15,0.15].
2) 由图 17速度-高度曲线可以看出,gPC方法、MC方法和确定性轨迹优化方法产生的均值轨迹基本一致.虽然气动干扰对轨迹生成产生了影响,但始终满足再入走廊下边界和终端约束等硬约束的指标,体现了gPC算法的有效性.
3) 由图 18、图 20、图 21可以看出,虽然gPC方法、MC方法与确定性轨迹优化方法产生的期望状态量基本一致,但是gPC更为接近确定性轨迹状态量.
4) 图 23~图 28显示了由气动偏差引起的状态量的均方差值,可以看出,状态量初始均方差都为零,高度、速度和弹道倾角呈现波动,但最终减小为零,验证了图 17中速度-高度棒形图中误差散布情况,同理,经度和纬度呈现逐渐增大的趋势,验证了图 18中纬度偏差逐渐增大的结论.
虽然gPC方法比MC方法的状态量均方差值略大,但最终形成的期望值与确定性轨迹优化生成的状态量更为接近.
5) 图 19中显示气动参数干扰下的落点,以均值落点为圆心,以最大落点偏差为半径的作圆.可以看出gPC方法比MC方法产生的散布更大,这是由于其状态量均方差更大造成的,但是由气动干扰产生了终端落点最大偏差为(-4.544°,5.056°),gPC方法估计的期望落点坐标为(62.044°,0.005°),不考虑气动干扰的落点坐标为(62.027°,0.089°),可见gPC方法估计的落点相较于MC方法更接近于确定性轨迹优化方法. 8 结 论
本文提出了基于广义正交多项式的随机最优轨迹优化数值解法,应用此方法对具有随机再入初值和气动干扰的高超声速滑翔式飞行器轨迹优化问题分别进行了数字仿真,得出以下结论:
1) gPC方法估计生成的轨迹与MC方法生成的均值轨迹都与确定性轨迹优化方法生成的轨迹基本一致,能满足各种约束条件的限制,且gPC方法效果稍微好一些,证明了gPC方法能够有效处理带有随机干扰的轨迹优化问题.
2) 初始偏差对于高度和速度产生的均方差有逐渐减小并趋近于零的趋势,但气动偏差对整个轨迹的影响一直存在.两者对轨迹产生的落点偏差均较大,因此在轨迹优化过程中必须考虑.
3) 在计算效率方法,gPC方法比MC方法大大提高,但gPC方法也不能作为在线轨迹优化方法,在计算时间上还有待提高.
4) gPC方法能够给出状态量的统计信息,有助于研究分析随机干扰对轨迹优化问题的影响因素,也可以为随机轨迹优化数值解法提供参考.
| [1] | Woolf A F.Conventional prompt global strike and long-range ballistic missiles:background and issues[R].ADA577938,2013 |
| [2] | 李惠峰,谢陵.基于预测校正方法的RLV再入制导律设计[J].北京航空航天大学学报,2009, 35(11):1344-1348 Li Huifeng,Xie Ling.Reentry guidance law design for RLV based on predictor-corrector method[J].Journal of Beijing University of Aeronautics and Astronautics,2009,35(11):1344-1348(in Chinese) |
| Cited By in Cnki (13) | |
| [3] | 王俊波,宋勋,宋剑爽,等.高超声速再入滑翔飞行器多约束轨迹快速优化[J].北京航空航天大学学报,2011,37(7):777-781 Wang Junbo,Song Xun,Song Jianshuang,et al.Rapid trajectory optimization for hypersonic reentry vehicles with multi-constraints[J].Journal of Beijing University of Aeronautics and Astronautics,2011,37(7):777-781(in Chinese) |
| Cited By in Cnki (4) | |
| [4] | 梁子旋,任章.基于在线气动参数修正的预测制导方法[J].北京航空航天大学学报,2013,39(7):853-857 Liang Zixuan,Ren Zhang.Predictive reentry guidance with aerodynamic parameter online correction[J].Journal of Beijing University of Aeronautics and Astronautics,2013,39(7):853-857(in Chinese) |
| Cited By in Cnki | |
| [5] | Rao A V,Clarke K A.Performance optimization of maneuvering re-entry vehicle using a legendre pseudospectral method[C]//AIAA Atmospheric Flight Mechanics Conference and Exhibit.Reston:AIAA,2002:1-13 |
| Click to display the text | |
| [6] | Xue S B,Ping L.Constrained predictor corrector entry guidance[J].Journal of Guidance Control and Dynamics,2010,33(4):1273-1281 |
| Click to display the text | |
| [7] | Xiu D.Efficient collocational approach for parametric uncertainty analysis[J].Communications in Computational Physics,2007,2(2):293-309 |
| Click to display the text | |
| [8] | Xiu D.Fast numerical methods for stochastic computations:a review[J].Communications in Computational Physics,2009,5(4):242-272 |
| Click to display the text | |
| [9] | Cottrill G C.Hybrid solution of stochastic optimal control problems using gauss pseudespectral method and generalized polynomial chaos algorithms[D].Ohio:Air University,2012 |
| [10] | Maj G C.Hybrid gauss pseudespectral and generalized polynomial chaos algorithms to solve stochastic trajectory optimization problems[C]//AIAA Guidance,Navigation,and Control Conference.Reston:AIAA,2011:6572-6588 |
| [11] | 雍恩米,唐国金,陈磊.基于Gauss伪谱法的高超声速飞行器再入轨迹快速优化[J].宇航学报,2008,29(6):1766-1772 Yong Enmi,Tang Guojin,Chen Lei.Rapid trajectory optimization for hypersonic reentry vehicle via gauss pseudospectral method[J].Journal of Astronautics,2008,29(6):1766-1772(in Chinese) |
| Cited By in Cnki (59) | Click to display the text | |
| [12] | Phillips T H.A common aero vehicle(CAV)model,description,and employment guide[R/OL].2003[2013-12-12].http://www.dtic.Mil/matrics/sbir/sbir041/srch/af031a.doc |
| Click to display the text | |
| [13] | Xiu D B.Numerical methods for stochastic computations:a spectral method approach[M].Princeton:Princeton University Press,2010 |
| [14] | 国海峰,黄长强,丁达理,等.多约束条件下高超声速导弹再入轨迹优化[J].弹道学报,2013,25(1):11-15 Guo Haifeng,Huang Changqiang,Ding Dali,et al.Re-entry trajectory optimization for supersonic missile considering multiple constraints[J].Journal of Ballistics,2013,25(1):11-15(in Chinese) |
| Cited By in Cnki (4) | |
| [15] | Benson D.A gauss pseudospectral transcription for optimal control[D].Cambridge:Massachusetts Institute of Technology,2005 |
