采用细长体机身的飞行器在大攻角下会产生前体非对称涡,进而诱导出非指令的摇滚运动[1].现代战机包括F-18 HARV[2]和X-31[3]均会产生前体非对称涡诱导的摇滚运动,尤其是X-31[3]随攻角会呈现包括滚转偏离、极限环振荡和发散等多种运动形态.Brandon和Nguyen[4]采用细长体和小后掠翼(Λ=26°)的组合体模型首次对前体非对称涡诱导机翼摇滚进行了实验研究.随后采用类似的模型,Ericsson[5, 6]、马宝峰[7]和邓学蓥等[8]都对这类摇滚运动进行了研究.研究发现,快速建立的极限环振荡是前体非对称涡诱导摇滚的典型运动形态,前体非对称涡左右涡位随滚转角的切换被认为是维持极限环机翼摇滚运动所必不可少的条件[4, 5, 6, 9].另外,人工扰动的研究明显促进了对于前体非对称涡诱导摇滚问题的研究:源于模型头尖部几何加工公差(自然扰动)的不确定性将使得细长体非对称涡形态也具有不确定性[10, 11],而在细长体头尖部添加的人工扰动[11, 12, 13, 14, 15]的周向位置与前体非对称涡涡型间具有确定的相关关系[16, 17],从而可以解决前体非对称涡的不确定性问题.在此基础上,马宝峰[7]和邓学蓥等[8]发现在细长体头尖部添加微颗粒人工扰动将使得自然扰动下原本没有确定性的自由摇滚运动变得具有确定性,并开展了人工扰动周向位置与前体非对称涡诱导摇滚运动相关关系的研究.
以上关于前体非对称涡诱导摇滚问题的研究都是在静态大攻角下展开的[1, 2, 3, 4, 5, 6, 7, 8, 9],然而现代战机通常是在攻角拉起机动中经历大攻角的.比如Su-27的“眼镜蛇”机动[18]就要求在2 s左右的时间内将战机从小攻角拉起到90°攻角;X-31“Herbst”机动[19]的第一步也是要求将战机拉起到过失速的大攻角.因此,本文着重研究攻角拉起时前体非对称涡诱导非指令摇滚运动及其机理.
1 实验模型及设备
实验在北京航空航天大学流体所D4低速风洞展开,风洞来流湍流度为0.08%.开口实验段尺寸为:2.5 m×1.5 m×1.5 m.文中实验的来流风速固定在Uo=25 m/s,相对模型圆柱段直径(D=90 mm)的雷诺数Re=UoD/ν≈1.6×105,ν为来流运动黏性系数.模型通过尾支撑固定在图 1(a)所示的动态拉起机构上,该机构能够驱动模型以恒定的角速度进行拉起运动,拉起攻角范围为α=0°~90°,拉起速度范围为ω=0.5~75(°)/s,对应的拉起减缩频率范围为ψ=ω·L/(360·Uo)=4.0×10-5~6.0×10-3,其中L=720 mm为模型长度.攻角运动由松下伺服电机驱动,连接模型支杆的摇臂和电机轴之间通过传动比分别为1∶5和1∶2的两级齿轮进行传动;攻角由与电机同轴的绝对式编码器(Koyo-TRD-NA10NW,精度10 bit)进行测量,其测量的攻角精度为0.035°.在攻角动态拉起时,通过引入比例-积分-微分(PID)的控制方法,使得机构对模型攻角的控制误差不超过0.5°.
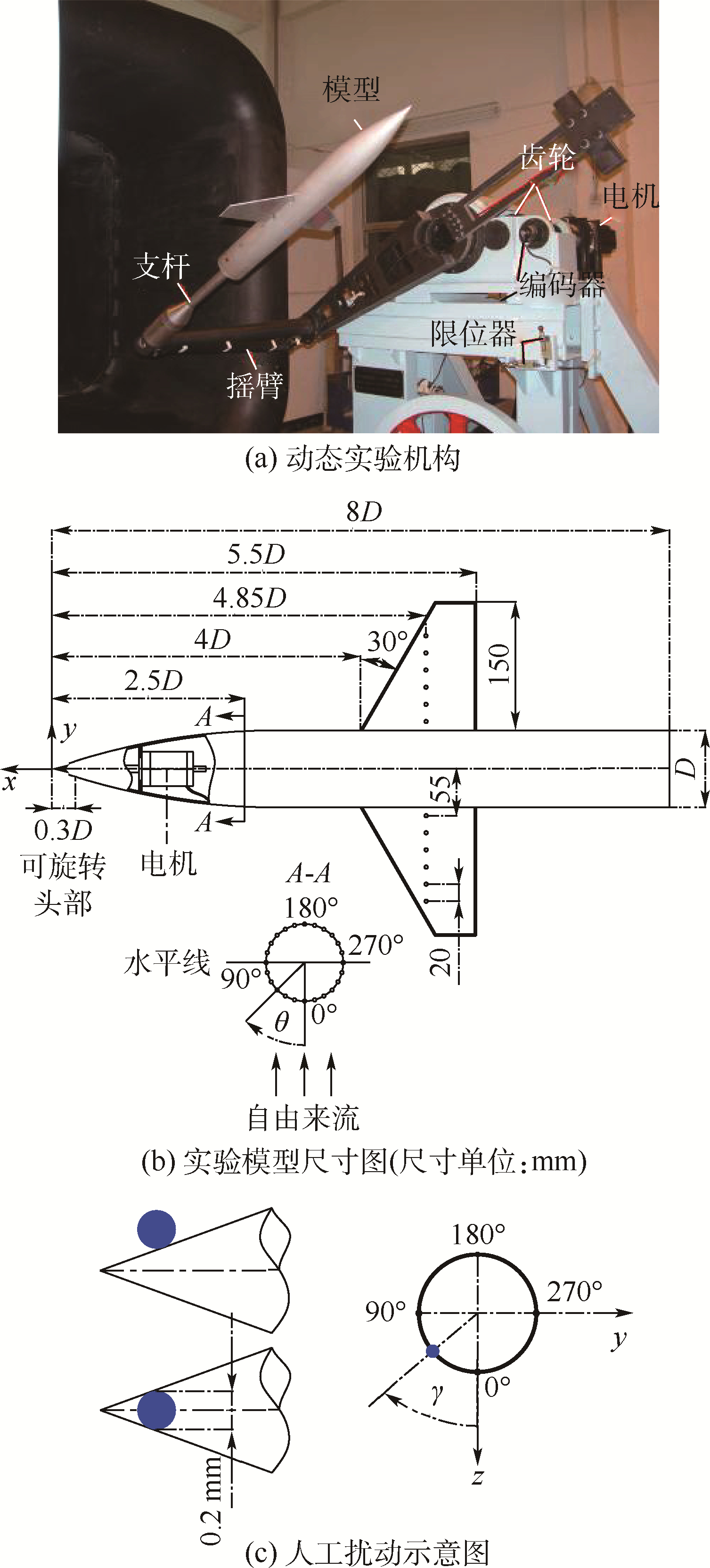 |
| 图 1 实验装置、模型及人工扰动 Fig. 1 Experimental set up,model and artificial perturbation |
实验模型如图 1(b)所示.模型机身为一个尖拱旋成体,30°后掠的梯形翼作为产生滚转力矩的前体非对称涡作用面安装在距模型尖端x/D=-4~-5.5的位置,机翼厚度4 mm.在x/D=-2.5的位置有24个等间距测压孔;模型迎风驻点位置定义为测压孔的0°/360°方位角θ,如图 1(b)中A-A视图所示;截面侧向力系数Cy由式(1)计算,其中Cp为测压孔的压力系数.在x/D=-4.85截面,两侧机翼各均布6个测压孔,截面滚转力矩系数Cl由式(2)计算.拉起运动的转心位于x/D=-5.5截面.模型头尖部可以通过安装在前体的电机进行驱动.整个实验模型由铝制成,绕x轴的转动惯量约为0.007 kg·m2.
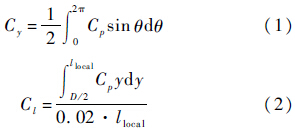
直径为0.2 mm的球形颗粒[20]作为人工扰动被黏贴于模型头尖部,如图 1(c)所示.人工颗粒扰动的轴向黏贴位置和周向位置γ的定义也如图 1(c)所示.在本文中人工扰动固定于γ=45°,此时前体非对称涡呈现为左侧涡位更低(沿x方向)的左涡型[15, 20].
自由摇滚运动时,模型与自由摇滚支杆[7]连接,安装在自由摇滚支杆尾端的编码器(12 bit)测得的滚转角精度为0.088°.在自由摇滚实验之前模型通过支杆内的电磁闸固定在滚转角$\phi $=0°处.在压力测量时,自由摇滚支杆将被替换为强迫摇滚支杆[9].通过安装在强迫摇滚支杆内的伺服电机,驱动模型复现自由摇滚时间历程,从而能够排除测压管道对摇滚运动的影响,实现拉起摇滚过程中的瞬时同步压力测量.强迫摇滚时模型滚转角由安装于支杆尾部的编码器测量,滚转角的测量精度为0.018°;强迫摇滚系统的滚转角复现误差不超过1.5°,该数值小于自由摇滚重复性实验时的滚转角误差.压力测量采用量程为±1 psi(6.895 kPa)、精度为0.1%FS的64通道压力扫描阀,其最大采集频率为330 Hz,文中动态测压时的最大采集频率为18 Hz,静态测压时的采集频率为200 Hz.模型表面测压孔与扫描阀之间通过外径1.0 mm的钢管和软管连接,管路的长度不超过80 cm;根据曹博超[21]的研究,100 cm长度的管路对10 Hz以下压力信号的滤波和迟滞作用很弱,而文中所关注的非对称涡所诱导的侧向力及滚转力矩等压力信号的频率小于10 Hz,因此本文认为所测量的压力结果真实可信.文中展示的动态压力和静态压力数据均为多次采样后的平均结果,采样次数分别为7次和600次.
2 实验结果与讨论
2.1 攻角拉起时摇滚运动形态 2.1.1 攻角静态时摇滚运动随攻角的变化曲线
在之前关于前体非对称涡诱导摇滚运动随攻角演化规律[4]的研究中并没有提及不确定性问题,但实验结果证实这一问题是实际存在的.图 2(a)给出了相同完全外形的两个不同头尖部下,摇滚运动随攻角的演化规律.图中的数据点表示摇滚运动稳定后第5 s至第20 s摇滚运动的平衡位置,竖线表示第5 s至第20 s摇滚运动的均方差,位于$\phi $=±90°的数据点表示自0°滚转角释放的模型将越过90°或-90°滚转角呈现为发散的运动形态.从图 2(a)中可以看出在非对称涡产生的27.5°~70°的攻角范围[22]内,两条曲线具有明显的不同.然而,如果在头尖部黏贴人工扰动,并将人工扰动固定于某一位置(γ=45°),自由摇滚随攻角的变化规律就是确定的,如图 2(b)所示.
 |
| 图 2 外形相同的两个头尖部下,摇滚运动平衡位置及均方差随攻角的变化规律(ω=0(°)/s) Fig. 2 Mean roll angle and standard deviation of free-to-roll motion with angle of attack for two nose tips with the same shape(ω=0(°)/s) |
由于前体非对称涡随攻角的变化[22, 23, 24, 25],在27.5°~70°攻角范围内的摇滚运动形态随攻角增加而变化,如图 3(a)所示;其中在31°~47.5°为较为剧烈的发散和振荡发散运动,运动时间历程分别如图 3(b)、图 3(c)所示,在其余攻角下则呈现为小振幅的滚转偏离和极限环振荡.在前体非对称涡对称的15°攻角附近,存在着机翼本身流动引起的滚转偏离运动.
 |
| 图 3 攻角静态时,摇滚运动随攻角的变化规律及发散、振荡发散时间历程曲线 Fig. 3 Free-to-roll motion changing with angle of attack and time histories for divergence as well as oscillating divergence when angle of attack is static |
2.1.2 不同拉起速度下摇滚运动随攻角变化曲线
为研究攻角拉起速度对摇滚运动的影响,本节在0°~85°的攻角范围内研究了系列拉起速度下的摇滚运动形态.图 4给出了3期实验所得摇滚运动振幅$\phi $Amp随拉起速度的变化曲线,其中振幅是单次拉起摇滚运动实验中滚转角绝对值的最大值,图 5给出了不同拉起速度下摇滚运动随攻角的变化曲线.从图中可以看出,在3个不同拉起速度分区内呈现出3种不同拉起摇滚运动形态:①当攻角拉起速度位于0.5~5(°)/s范围内时,摇滚运动随攻角会呈现出偏离、发散和极限环振荡等形态,如图 5(a)所示;②当攻角拉起速度位于10~25(°)/s时,摇滚运动随攻角呈现为发散的运动形态,如图 5(b)所示;③当攻角速度位于32.5~75(°)/s时,摇滚运动呈现为一个周期左右的类正弦振荡形式,摇滚振幅在30°左右,运动形态相比前两个拉起速度分区下的运动形态较为缓和,15°攻角附近的滚转偏离也不再产生,如图 5(c)所示.另外,从图 4的结果也可以看出,当拉起速度位于3个拉起速度分区之间时,摇滚运动形态不具有重复性.
 |
| 图 4 摇滚运动振幅随攻角拉起速度的变化曲线 Fig. 4 Curves of amplitude of free-to-roll motion changing with pitch rate |
 |
| 图 5 不同拉起速度下摇滚运动随攻角的变化曲线 Fig. 5 Curves of free-to-roll motion changing with angle of attack for different pitch rates |
2.1.3 拉起减缩频率对拉起摇滚运动的影响
对于拉起速度对摇滚运动影响的研究是否具有普遍性的意义,图 6给出了两个不同无量纲拉起减缩频率ψ下的拉起摇滚运动曲线.从图 6中可以看出,尽管来流风速Uo和拉起速度ω都发生了变化,但只要拉起减缩频率维持不变,摇滚运动形态就大致相同;而当拉起减缩频率改变后,摇滚运动形态即发生明显的变化.在相同拉起减缩频率下,图 6中不同拉起速度(来流风速)下的摇滚曲线在幅值和相位上仍然有一定差异,比如图 6(b)中,拉起速度(来流风速)越大,幅值就越大,除了摇滚运动自身的重复性影响以外,另一个重要的原因为支杆摩擦力:来流风速越大,驱动摇滚的滚转力矩的数值就越大,那么摩擦力的影响就相对越小,从而摇滚的振幅就相对较大、可以想象,当风速降为0.5 m/s甚至更小时,较小的滚转力矩将不能克服支杆的摩擦力作用,模型就不会再产生拉起摇滚运动.
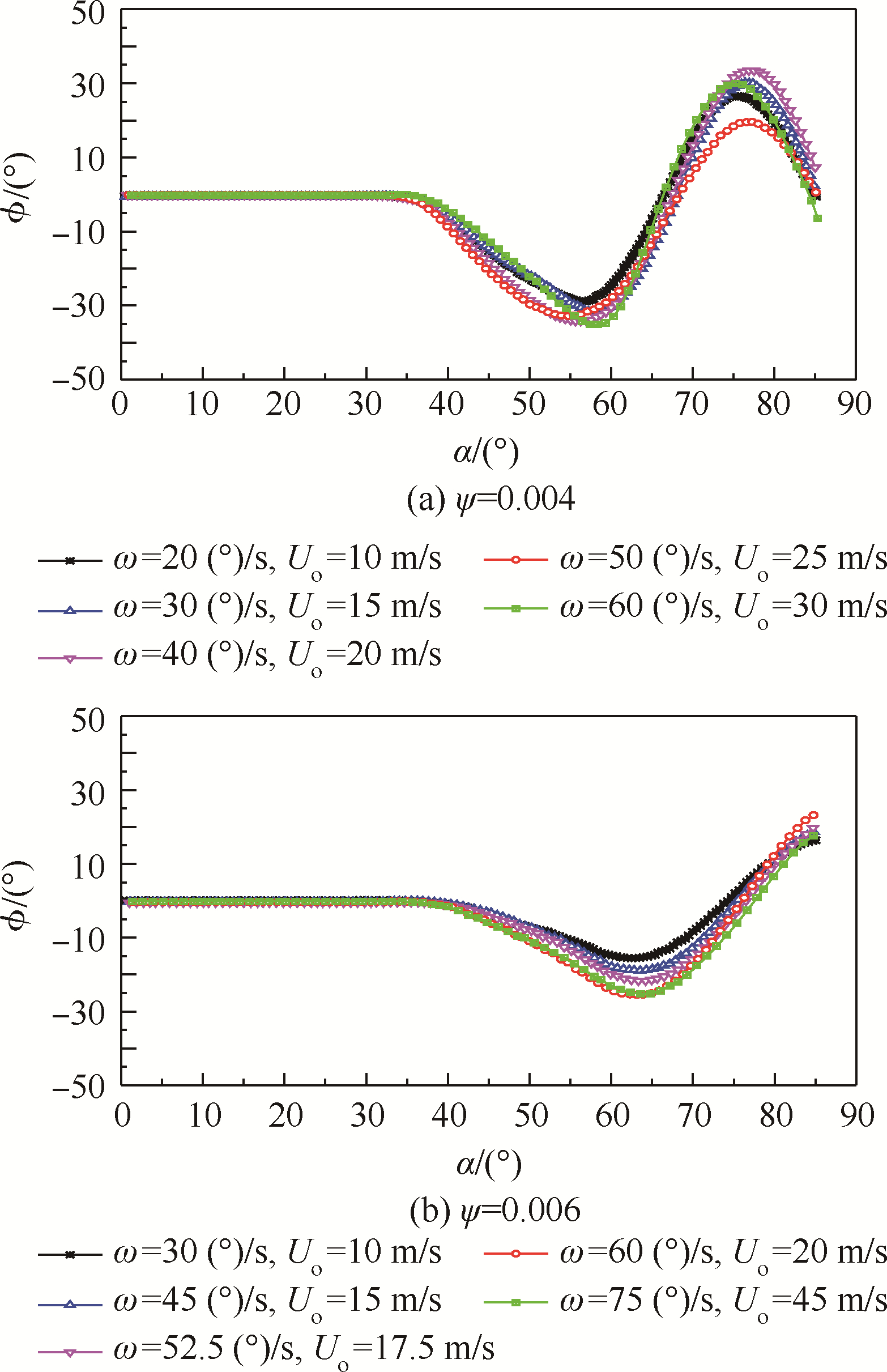 |
| 图 6 不同拉起减缩频率下的摇滚运动 Fig. 6 Free-to-roll motions for different reduced frequencies |
除了无量纲拉起减缩频率以外,来流Re数由于决定了前体非对称涡的分离类型和强度[26]也必然对拉起摇滚运动形态有重要的影响,但由于本文Re数小于2.0×105,前体流动始终处于亚临界Re区(前体两侧边界层分离形态为层流),因此Re数效应还没有显现出来.
2.2 攻角拉起时摇滚运动的机理分析 2.2.1 摇滚运动随拉起速度分区效应的机理分析
从第2.1.2节的实验结果可以看出,当攻角拉起速度增加到较快的第③分区(32.5~75(°)/s)时,摇滚运动的形态由发散变为振幅约30°左右的类正弦振荡,运动形态突然变得“缓和”,这一显著变化可从图 7得出原因.
 |
| 图 7 不同拉起速度时摇滚运动随攻角变化曲线对比 Fig. 7 Comparison of curves of free-to-roll motions changing with angle of attack for different pitch rates |
图 7给出了攻角静态和两个典型拉起速度下摇滚运动随攻角的变化曲线,从图中可以看出发散运动发生的攻角范围为31°~47.5°,拉起速度位于第②分区10~25(°)/s时的发散运动均发生在该攻角范围内.对于摇滚来说,其滚转角时间历程可表达为
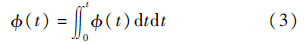
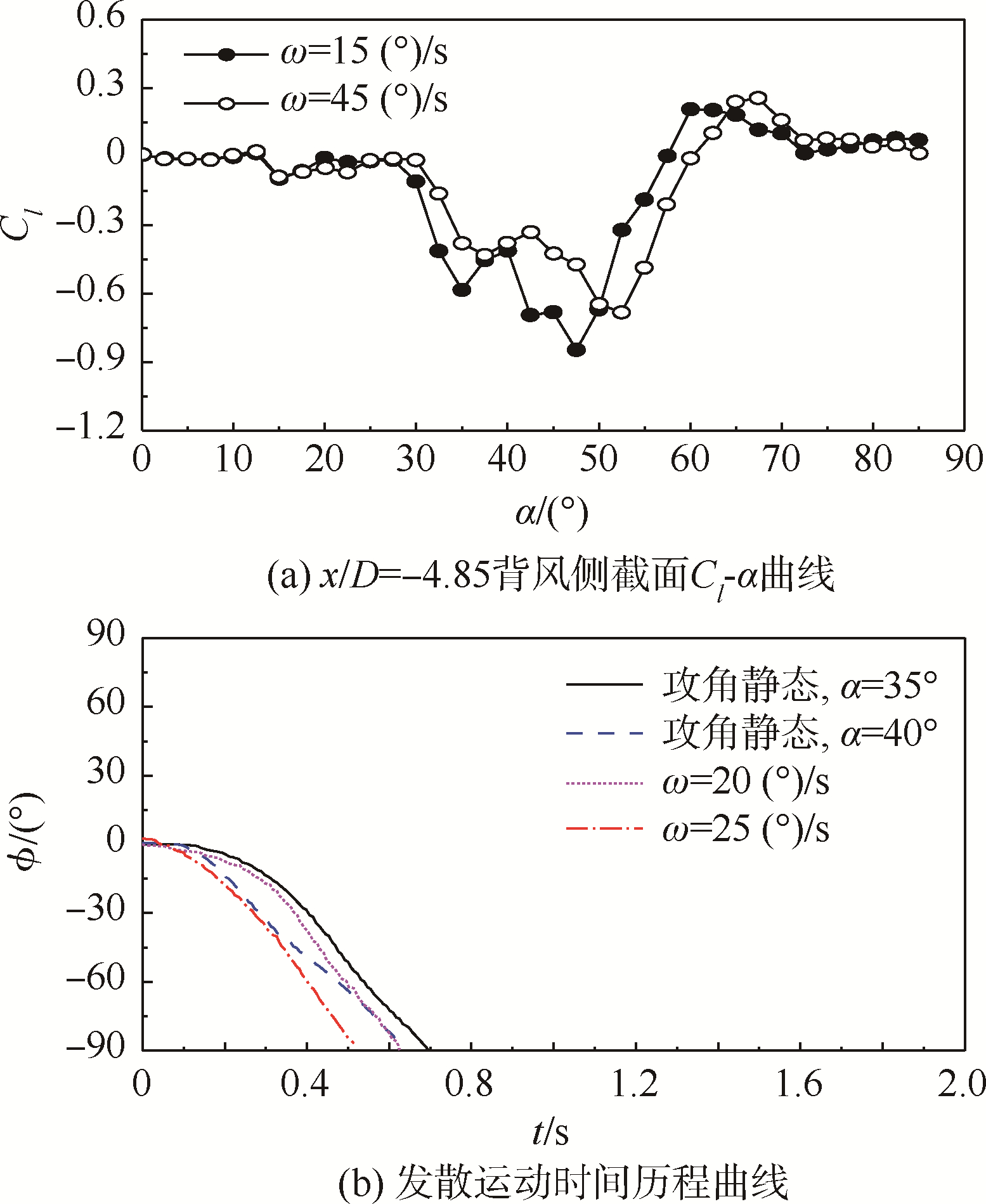 |
| 图 8 拉起速度对机翼背风侧截面滚转力矩系数和摇滚时间历程曲线的影响 Fig. 8 Effects of pitch rate on leeward sectional rolling moment coefficient and on time history of free-to-roll motion |
2.2.2 快速拉起类正弦振荡的机理分析
以往对于攻角静态时摇滚运动的机理分析,往往通过流动及滚转力矩等随滚转角的变化特性来展开.但对于攻角快速拉起时的摇滚,由于涉及到滚转和攻角拉起两个自由度的运动,其分析也将有所不同.图 9给出了快速拉起机翼摇滚过程中Cy-α及Cl-α曲线与固定0°滚转角单独快速拉起(拉起速度与前者相同)过程中Cy-α及Cl-α曲线对比.图 9(a)表明两种情形下侧向力随攻角的变化曲线基本相同,即主控摇滚的前体非对称涡在摇滚过程中没有发生明显的变化;图 9(b)所示两种情形下滚转力矩系数随攻角的变化曲线则表明:对于背风侧的滚转力矩,滚转运动对其也没有本质上的影响.因此,在快速拉起时,前体非对称涡及其诱导滚转力矩随滚转角的变化对于摇滚的分析相对次要,二者随攻角的变化更为重要.
 |
| 图 9 攻角拉起类正弦振荡与单独攻角拉起($\phi $=0°)两种情形下Cy-α及Cl-α曲线对比(ω=40(°)/s) Fig. 9 Comparison of Cy-α and Cl-α curves with $\phi $=0° in pitch-up and during sinusoidal-like oscillation in pitch-up (ω=40(°)/s) |
另外,从图 9中也可以看出,在攻角超过70°以后,由于前体流动逐渐进入类卡门涡区[22, 23, 24, 25],滚转力矩接近于0,因此快速拉起时70°攻角以后的类正弦振荡应该是摇滚的一个收敛过程.
3 结 论
1) 摇滚运动随攻角的变化规律随攻角拉起速度呈现出明显的分区特性:在拉起速度位于0.5~5(°)/s的第①分区时,摇滚运动随攻角的演化规律与攻角静态时的结果相似,呈现出包括偏离、极限环振荡以及发散等运动形态;在拉起速度位于10~25(°)/s的第②分区时,模型连续旋转;而拉起速度位于32.5~75(°)/s的第③分区时,非指令摇滚运动形态呈现为周期数较少的类正弦形式振荡;拉起速度位于3个分区之间时,摇滚运动不具有重复性.
2) 攻角拉起的无量纲减缩频率是主控攻角拉起时摇滚运动形态的重要无量纲参数,在亚临界Re数下,拉起无量纲减缩频率不变,拉起摇滚运动的形态就基本维持不变.
3) 当拉起速度较大时,模型将没有足够的时间完成从0°~90°滚转角的发散运动,这是摇滚运动形态随攻角拉起速度具有分区效应的关键原因.
4) 与固定攻角时自由摇滚不同,流动随滚转角的变化对快速拉起时自由摇滚运动并没有决定性的影响,取而代之的是流动随攻角的变化,即Cl-α曲线取代Cl-$\phi $曲线,成为快速拉起摇滚分析的关键.
| [1] | Katz J.Wing/vortex interactions and wing rock[J].Progress in Aerospace Sciences, 1999, 35:727-750. |
| Click to display the text | |
| [2] | Quast T, Nelson R C, Fisher D F.A study of high alpha dynamics and flow visualization for a 2.5% model of the F-18 HARV undergoing wing rock[J].AIAA, 1991, 3267-CP:524-533. |
| [3] | Klein V, Noderer K D.Aerodynamic parameters of the X-31 drop model estimated from flight data at high angles of attack[J].AIAA, 1992, 4357:174-181. |
| [4] | Brandon J M, Nguyen L T.Experimental study of effects of forebody geometry on high angle of attack stability[J].Journal of Aircraft, 1988, 25(7):591-597. |
| Click to display the text | |
| [5] | Ericsson L E.Wing rock generated by forebody vortices[J].Journal of Aircraft, 1989, 26(2):110-116. |
| Click to display the text | |
| [6] | Ericsson L E.Further analysis of wing rock generated by forebody vortices[J].Journal of Aircraft, 1989, 26(12):1098-1104. |
| Click to display the text | |
| [7] |
马宝峰.前体涡诱导机翼摇滚的实验研究[D].北京:北京航空航天大学, 2007. Ma B F.Experimental investigation of roll oscillation induced by forebody vortex[D].Beijing:Beihang University, 2007(in Chinese). |
| [8] | Wang B, Deng X Y, Ma B F, et al.Effect of tip perturbation and wing locations on rolling oscillation induced by forebody vortices[J].Acta Mechanica Sinica, 2010, 26(5):787-791. |
| Click to display the text | |
| [9] |
荣臻.前体涡诱导机翼摇滚的流动特性及机理研究[D].北京:北京航空航天大学, 2009. Rong Z.An experimental investigation on flow characteristics and mechanism of wing rock induced by forebody vortex[D].Beijing:Beihang University, 2009(in Chinese). |
| [10] | Dexter P C, Hunt B L.The effect of roll angle on the flow over a slender body of revolution at high angles of attack[J].AIAA, 1981, 0358:1-13. |
| [11] | Zilliac G G, Degani D, Tobak M.Asymmetric vortices on a slender body of revolution[J].AIAA, 1991, 29(5):667-675. |
| Click to display the text | |
| [12] | Dexter P C.A study of asymmetric flow over slender bodies at high angles of attack in a low turbulence environment[J].AIAA, 1984, 0505:1-11. |
| Click to display the text | |
| [13] | Moskovitz C A, Raleigh N C, Hall R M, et al.Effects of surface perturbations on the asymmetric vortex flow over a slender body[J].AIAA, 1988, 0483:1-10. |
| Click to display the text | |
| [14] | Moskovitz C A, Hall R M, Dejarnette F R.Effects of nose bluntness, roughness and surface perturbations on the asymmetric flow past slender bodies at iarge angles of attack[J].AIAA, 1989, 2236-CP:720-732. |
| Click to display the text | |
| [15] | Chen X R, Deng X Y, Wang Y K, et al.Influence of nose perturbations on behaviors of asymmetric vortices over slender body[J].Acta Mechanica Sinica, 2002, 18(6):581-593. |
| Click to display the text | |
| [16] | Hunt B L.Asymmetric vortex forces and wakes on slender bodies[J].AIAA, 1982, 1336:1-41. |
| Click to display the text | |
| [17] | Lamont P J.Pressures around an inclined ogive cylinder with laminar, transitional, or turbulent separation[J].AIAA, 1982, 20(11):1492-1499. |
| Click to display the text | |
| [18] | Li Y P, Ge F Y, Lan C E.Estimation of aircraft models in cobra maneuver through dynamic inversion[J].AIAA, 1994, 3494-CP:322-332. |
| [19] | Alcorn C W, Croom M A, Francis M S, et al.The X-31 aircraft:Advances in aircraft agility and performance[J].Progress in Aerospace Sciences, 1996, 32:377-413. |
| Click to display the text | |
| [20] |
田伟.细长旋成体及融合体型机身大迎角背涡流动特性研究[D].北京:北京航空航天大学, 2010. Tian W.Study on behaviors of leeward vortices over slender body and chined fuselage at high angle of attack[D].Beijing:Beihang University, 2010(in Chinese). |
| [21] |
曹博超.风洞动态测压技术及其在机翼摇滚运动研究中的应用[D].北京:北京航空航天大学, 2008. Cao B C.Dynamic pressure measurement technology in the wind tunnel and its application in the investigation of wing-rock phenomenon[D].Beijing:Beihang University, 2008(in Chinese). |
| [22] |
王刚,邓学蓥,王延奎,等.亚临界雷诺数细长体绕流流态随迎角的变化和分区[J].流体力学实验与测量, 2003, 17(2):19-26. Wang G, Deng X Y, Wang Y K, et al.Zonal study of flow patterns around an ogive-cylinder at subcritical reynolds numbers[J].Experiments and Measurements in Fluid Mechanics, 2003, 17(2):19-26(in Chinese). |
| Cited By in Cnki (15) | |
| [23] | Lamont P J, Hunt B L.Pressure and force distributions on a sharp-nosed circular cylinder at large angles of inclination to a uniform subsonic stream[J].J Fluid Mech, 1976, 76(3):519-559. |
| Click to display the text | |
| [24] | Keener E R, Chapman L C, Talegbani J.Side forces on a tangent ogive forebody with a fineness ratio of 3.5 at high angles of attack and mach numbers from 0.1 to 0.7[J].NASA, 1977, TM, X-3437:1-109. |
| Click to display the text | |
| [25] | Ericsson L E, Reding J P.Aerodynamic effects of asymmetric vortex shedding from slender bodies[J].AIAA, 1985, 1797:222-256. |
| Click to display the text | |
| [26] | Lamont P J.Pressures around an inclined ogive cylinder with laminar, transitional, or turbulent[J].AIAA, 1980, 1556R:1-10. |
| Click to display the text |





