Download PDF  
文章快速检索  
  高级检索
引用本文
张洪礼, 罗钦钦, 韩潮. UKF参数估计在三体Lambert问题中的应用[J]. 北京航空航天大学学报, 2015, 41(2): 228-233
ZHANG Hongli, LUO Qinqin, HAN Chao. Application of UKF parameter estimation in the three-body Lambert problem[J]. Journal of Beijing University of Aeronautics and Astronsutics, 2015, 41(2): 228-233.
UKF参数估计在三体Lambert问题中的应用
张洪礼1, 罗钦钦2, 韩潮1    
1. 北京航空航天大学 宇航学院, 北京 100191;
2. 北京空天技术研究所, 北京 100074
收稿日期 : 2014-03-12; 录用日期 : 2014-04-10; 网络出版日期 ： 2014-05-07
基金项目：载人航天预研资助项目(010103).
作者简介: 张洪礼(1988—), 男, 山东威海人, 博士生, zhanghongli@buaa.edu.cn
通讯作者: 韩潮(1960—), 男, 北京人, 教授, hanchao@buaa.edu.cn, 主要研究方向为航天器动力学与控制、航天器导航、制导与控制、航天系统动力学仿真等.
摘要：为了快速精确地求解三体Lambert问题,提出了一种新的基于无损卡尔曼滤波(UKF)参数估计的数值求解算法,该算法由初值猜测和精确解求解两部分组成.首先,基于地月系统二体模型,通过简单迭代求解三体Lambert问题的初值.然后,将三体Lambert问题对应的两点边值问题转化为参数估计问题,通过UKF滤波算法求解,可得到收敛的精确解.该算法是基于概率估计理论的,不仅避免了传统数值方法推导相关梯度矩阵的复杂性,而且降低了三体Lambert问题对初值精确度的要求,从而显著降低了三体Lambert问题求解的难度.数值仿真表明,该方法求解效率较高,具有良好的鲁棒性,与微分修正算法、二阶微分修正算法对比具有更大的收敛域.
关键词： 三体系统     Lambert问题     两点边值问题     无损卡尔曼滤波     参数估计    
Application of UKF parameter estimation in the three-body Lambert problem
ZHANG Hongli1, LUO Qinqin2, HAN Chao1     
1. School of Astronautics, Beijing University of Aeronautics and Astronautics, Beijing 100191, China;
2. Beijing Aerospace Technology Institute, Beijing 100074, China
Abstract:A new algorithm based on unscented Kalman filter (UKF) parameter estimation was proposed for the fast and efficient solution of the three-body Lambert problem. The algorithm was divided into two steps, guessing the initial solution and searching the exact solution. The initial solution of the three-body Lambert problem was generated using the two-body model of the Earth-Moon system. Then the two-point boundary value problem corresponding to the original three-body Lambert problem was converted to a parameter estimation problem. Through solving the converted problem using UKF, the converged exact solution was found. The algorithm was based on the theory of probability, so the derivation of the gradient matrixes required by traditional numerical methods was omitted. Moreover, the demand for the accuracy of the initial solutions for the three-body Lambert problem was modified. Therefore, the difficulty of solving the three-body Lambert problem was greatly reduced. Numerical examples indicate that the algorithm is of high efficiency and robustness and obtains a larger convergence domain compared with the differential-correction method and the second order differential-correction method.
Key words: three-body systems     Lambert problem     two-point boundary value problem     unscented Kalman filter     parameter estimation    

在航天器轨道动力学中,最著名的两点边值问题是二体Lambert问题,即在一中心引力场中,求解经过两位置矢量 R 1和 R 2、转移时间为Δt12的开普勒轨道.到目前为止,已有大量学者对二体Lambert问题进行了深入广泛的研究,文献[1, 2, 3]等都给出了经典的求解方法.二体Lambert问题的特点是中心引力场为主要影响因素,其余影响可作为摄动考虑,主要应用于近地轨道设计.但是,在深空轨道设计中,需要考虑第三体引力影响,不能单纯将其作为摄动处理,否则会导致很大误差,这就引入了三体Lambert问题.与二体Lambert问题相比,三体Lambert问题的边值条件是相同的,但由于第三体引力不可作为摄动考虑,增加了动力学模型的非线性程度,使得问题求解更加困难.由于三体问题不存在解析解,三体Lambert问题必须依靠数值方法求解,其本质上是一个两点边值问题,一般的求解过程分为两步:首先根据边值约束猜测初值,然后通过数值预报对轨道进行精确预报,采用微分修正等数值方法对初值进行修正,最终得到收敛的精确解.

本文选取存在一次相对次天体引力辅助变轨的三体Lambert问题,作为一般三体Lambert问题的一类特例,此类问题可作为多次引力辅助转移轨道设计[4, 5]的基础模块,可用于地月间[6, 7]或地火间[8]轨道设计中,还可用于平动点轨道设计[9, 10]中,有较大的研究价值.针对三体Lambert问题的求解,文献[11]提出了一种简单迭代算法,但文中没有给出搜索变量初值的估计方法.文献[12]利用伪状态理论,将相对于次天体的近拱点以及相应的位置速度作为设计变量,构建一个7维的微分修正,迭代搜索飞掠次天体的转移轨道,但文中同样没有给出猜测初值的方法.文献[13]将转移轨道按其形态上的特点进行归纳分类,建立初值样本库,然后根据给定两点的相对位置关系,从样本库中选择合适的初值,进而进行精确轨道搜索,但这种方法需要设计者具有十分丰富的深空轨道设计经验,对特定的约束选择合适的设计初值,人工干预较大.文献[14]在微分修正算法的基础上,推导并利用二阶微分修正算法,通过伪状态理论给出的初值,可获得收敛的精确解,但二阶微分修正算法的收敛性能仍然有限,尤其对于转移时间较长、飞掠高度较低的情况,转移轨道对于近拱点状态是十分敏感的,可能会导致搜索过程不断振荡,甚至发散.

针对以上研究现状,本文提出一种基于无损卡尔曼滤波(UKF)参数估计算法的三体Lambert问题求解方法.首先,只需基于二体Lambert问题在惯性空间中求解出初始设计结果,然后将原问题的求解转化为参数估计问题,利用UKF参数估计算法求解真实摄动环境下的精确转移轨道,就可以得到收敛的精确解.UKF滤波算法是基于概率估计理论的,不依赖于梯度信息,在初值精度不高的情况下仍然可以获得收敛的最终解.同时,该方法避免了微分修正算法等传统数值方法推导相关梯度矩阵的复杂性,从而大大降低了问题求解的难度.除此之外,该方法又具有较好的收敛性和准确性,可用来有效地求解高非线性程度、高敏感性的三体Lambert问题.

1 问题描述

三体Lambert问题的定义是,在三体系统中,求解经过给定位置矢量 R 1和 R 2、转移时间为Δt12的转移轨道.令起始点速度矢量记为V 1,经过时间Δt12后,转移轨道位置矢量为 R′ 2,定义函数F:

其中F是 V1的函数,则三体Lambert问题的数学描述为求解下述方程的根:
上述方程没有解析解,只能通过数值方法求解,但其非线性程度很高,一般情况存在多个解,很难确定其解得个数并将其全部求出.本文以地月系为例,地月系中两天体间距相对较小,质量比相对较大,故非线性程度和敏感性相对较高,考虑R 1和 R 2都位于月球影响球之外,并且要求转移轨道经过月球影响球(否则可采用二体Lambert近似),如图 1所示.

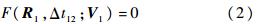
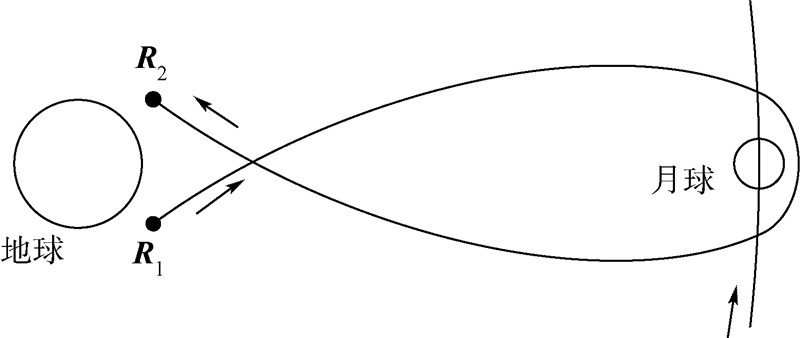图 1 三体Lambert问题示意图Fig. 1 The three-body Lambert problem
图选项
2 基于二体模型的初值猜测

在三体Lambert问题的初始设计阶段,不需要在整个转移轨道上都考虑月球的影响,而仅仅在月球飞掠时,考虑由于月球引力引起的入射速度和出射速度之间的方向改变,其余都是地心圆锥曲线轨道.

假设起始点位置矢量为 R 1,起始时刻为t1,终止点位置矢量为 R 2,终止时刻为t2,则总转移时间为Δt12=t2－t1,初值猜测算法流程见图 2,详细步骤如下:

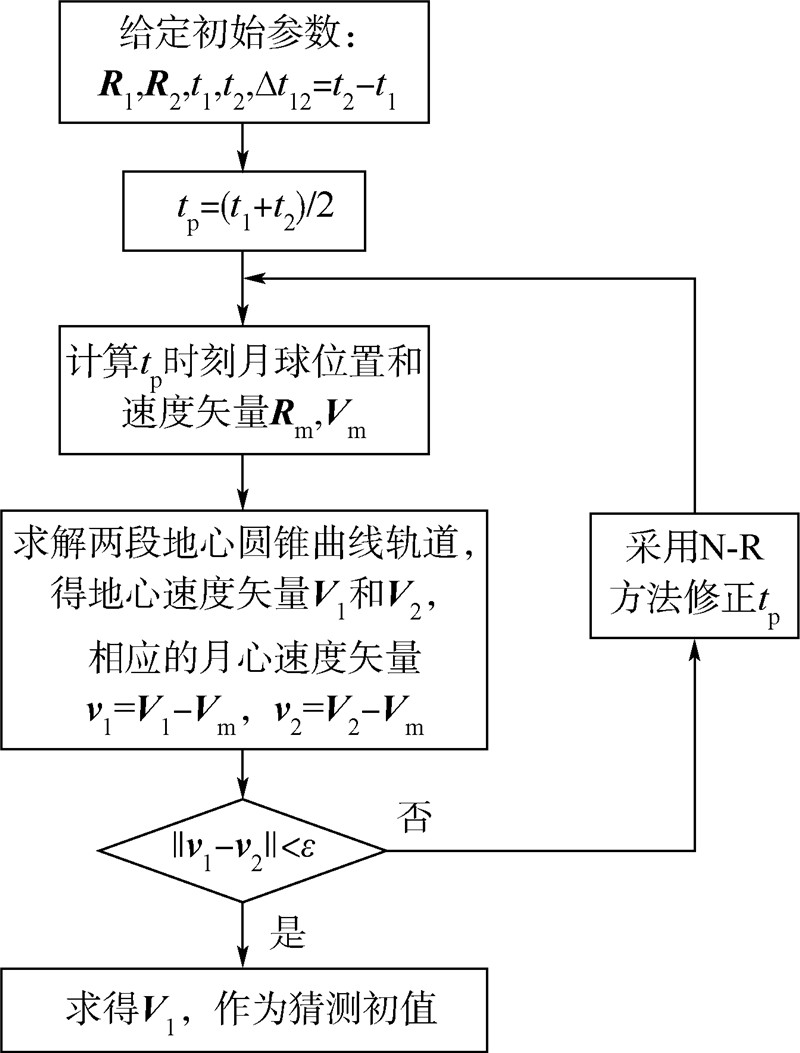图 2 初值猜测流程图Fig. 2 Initial guess flowchart
图选项

1) 将近月点时刻记为tp,令tp=(t1+t2)/2,计算tp时刻月球的位置和速度向量 R m,V m.

2) 求解从 R 1到 R m、转移时间为tp－t1和从 R m到 R 2、转移时间为t2－tp的两段地心圆锥曲线轨道,由此可以得到 R m处的地心速度矢量 V 1,V2,相应的月心速度矢量为 v 1= V 1－ V m,v 2= V2－Vm.

3) 若 ||v 1－ v 2||大于或等于给定阈值,则采用牛顿-拉弗逊方法调整tp,返回步骤2).若 ||v 1－ v2||小于给定阈值,则迭代终止.

4) 计算 R 1处速度矢量V1,即求得猜测初值,作为下一步精确解求解的基础.

3 UKF参数估计及其求解方法

参数估计问题,又被称为系统辨识或机器学习问题,其目的是确定某个非线性映射:

该映射的输入量为 xk,输出量为 xk,w 为非线性映射的参数.一般来说,映射的输入量 xk和期望输出量 dk是不变的,输出误差定义为 ek= dk－ G ( xk,w).求解参数估计问题就是要估计 w的均值,使映射 G( xk,w )的输出误差最小.

将原始参数估计问题写成状态空间表达式:

该式代表一个状态转移矩阵为单位阵的静态过程.rk过程噪声;期望输出dk则与对 wk的非线性观测相对应; ek为观测噪声. 由此,原始参数估计问题就可以用扩展卡尔曼滤波(EKF),无损卡尔曼滤波(UKF),粒子滤波(PF)等滤波器求解.从优化问题的角度看,上述参数估计问题相当于求解性能指标如下以w为优化变量的优化问题:
其中,Re为观测噪声的方差阵,若 Re为常值对角阵,则可以提到求和符号之外而不影响问题的求解,因此可以任意设定.过程噪声 rk的方差阵 Rkr=E[rk rkr] 则影响滤波器的收敛速度和跟踪性能.一般来说,Rkr越大,当前状态的滤波值中早期数据所占的比例就衰减得越快,越突出新息的作用.用滤波器求解参数估计问题的相关理论,文献[15]作了详细阐述,本文只作简要介绍.这里直接给出基于UKF滤波器的参数估计算法流程,如图 3所示.其中：
图 3 UKF参数估计流程图Fig. 3 UKF parameter estimation flow chart
图选项
N是 w的维数；η是尺度参数；常量ε决定了无损变换(UT)的σ点相对于w 当前均值的分布范围,一般设为小量,取值范围为[10－4,1]；常量κ一般取为0或者3－N；β是与 w 的先验分布相关的常量,对于高斯分布,β=2是最优的.ρRLS是遗忘因子,用于防止因模型误差较大造成的滤波发散,其取值范围为(0,1].α是权重因子,取值范围为[0,1].

4 UKF参数估计算法求解精确解

由于三体问题不存在解析解,所以只能通过数值积分对转移轨道进行精确预报,在猜测初值的基础上进行改进,最终求得精确解.

将式(2)代表的三体Lambert问题改写为参数估计问题,选择待估计参数wk为起始点地心速度矢量V1,输出dk为 R2,输入xk包括起始点位置矢量R1、起始时刻t1、终止时刻t2,则该问题可以表示为

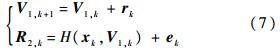
其中 rk和ek分别为系统噪声和观测噪声.显然,式(4)与式(7)形式上一一对应,因而三体Lambert问题的精确解求解已转化为参数估计问题,可以通过第3节的UKF参数估计算法求解.另外,待估计参数wk的各分量需要进行单位化,以利于精确解的搜索过程.

值得注意的是,在求解三体Lambert问题的精确解的过程中,UKF滤波收敛的过程受算法中若干可调参数的影响很大,如系统噪声矩阵 Rr、尺度参数常量ε、遗忘因子ρRLS和权重因子α 等,如选取不合适,则会导致滤波收敛过程的振荡幅度很大,不能较快收敛,甚至发散.这些量的选取和更新方法属于UKF滤波器算法的改进范畴,不是本文的讨论重点,可以作为下一步工作.本文通过大量数值仿真,总结算法中各个可调参数的推荐值,以供参考,如表 1所示.

表 1 UKF参数估计算法中的可调参数推荐值 Table 1 Reference values of adjustable parameters in the UKF parameter estimation method
参数取值
系统噪声协方差阵Rr对角线元素为10－4
尺度参数常量ε5×10－4或8×10－4
遗忘因子λRLS0.1
权重因子α0.5
表选项
5 算例与分析

本节给出一个包含引力辅助变轨的三体Lambert问题的求解算例.在J2000坐标系中,起始点R1坐标为[5048258,893447,-33213306],终止点 R2坐标为[9472144,-7816649,31557762],单位均为m,转移时间为2014-01-01—2014-01-07,整个转移时间为6d.此算例起始点和终止点的位置在地球附近,类似于地月自由返回轨道的边值条件,终端状态相对于起始状态具有很高的敏感度.

首先,利用基于二体模型的初值猜测方法,可得到该三体Lambert问题的初值为 V1=[2924.54,-2100.25,-3000.33],单位均为m/s.为利于精确解的搜索,单位化后的 V1作为待估计参数wk.

接下来,在初值的基础上,进一步对初值进行修正,以获得三体Lambert问题的收敛的精确解.在这里对微分修正算法和UKF参数估计算法进行对比,精确解搜索的收敛标准为终点位置误差在1m以内.从以上的初值出发,精确解的搜索过程见表 2和表 3.其中,表 2为微分修正算法的搜索过程,从表中可得出,其搜索过程是不断震荡甚至是发散的,表 3为UKF参数估计算法的搜索过程,从表中可得出,经过12次迭代后,其搜索过程最终收敛.

表 2 微分修正算法精确解搜索过程Table 2 Iteration of searching the final solution using the differential-correction method m
迭代次数ΔxΔyΔz
1-4.82×106-3.06×1083.11×106
2-1.17×109-7.17×1073.87×108
3-5.36×107-1.01×1073.69×107
4-1.53×107-5.33×1061.85×107
5-1.03×1081.56×1078.10×107
6-1.25×1093.71×108-7.42×108
7-1.28×1083.35×107-4.29×107
8-1.72×1083.64×1071.10×108

表选项
表 3 UKF参数估计算法精确解搜索过程Table 3 Iteration of searching the final solution using the UKF parameter estimation method m
迭代次数ΔxΔyΔz
1-4.82×106-3.06×1083.11×106
2-1.10×1089.77×107-5.58×106
3-4.13×1063.51×1076.43×107
4-5.69×1061.27×1063.98×106
....
....
....
91.62×103-7.83×1023.39×103
101.06×102-5.03×1012.22×102
114.22×100-1.90×1008.67×100
121.10×10-1-3.95×10-22.09×10-1

表选项

由此,UKF参数估计算法在解决三体Lambert问题中的有效性得以验证,并且UKF参数估计算法比微分修正算法具有更大的收敛域.该三体Lambert问题最终的飞行轨迹见图 4.

图 4 三体Lambert问题的飞行轨迹Fig. 4 Trajectory of the three-body Lambert problem
图选项

为了详细研究UKF参数估计算法的收敛域,并与微分修正算法、二阶微分修正算法[14]进行对比,可以采取下面方法.对于上述算例最终解的某一个分量添加扰动,而另外两个分量保持不变.从这个扰动点出发,分别使用微分修正算法、二阶微分修正算法和UKF参数估计算法来搜索转移轨道的精确解,不断增加扰动量,一直到精确解搜索过程发散,由此得到这3种算法对于特性的扰动分量的收敛域.虽然这不是该问题收敛域的完整描述,但是也部分揭示了各种算法收敛域的基本特性,也可以体现各种算法的优劣.3种精确解搜索算法的收敛域统计信息见表 4.

表 4 各算法的收敛域统计Table 4 Statistics of convergence domains of various methods m/s
扰动分量收敛域
微分修正二阶微分修正UKF参数估计
V1,x6.36.929.2
V1,y1.010.222.9
V1,z0.30.47.6
表选项

上述结果可以得出结论:①设计变量 V 1的单个分量收敛域与约束条件之间没有特定的规律,而仅仅有很大的变化区间,体现了该问题收敛域具有十分复杂的几何结构,这也是由于三体Lambert问题的高度非线性特性导致的;②在保证相当精度的情况下,平均水平上看,UKF参数估计算法的收敛范围是微分修正算法、二阶微分修正算法收敛域的3~5倍.另外,对于3种算法均收敛的算例,在Intel Core 2.53GHz,3GB RAM的计算条件下,微分修正算法、二阶微分修正算法、UKF参数估计算法的平均计算时间分别为1.96,2.70,14.95s.

为了进一步研究UKF参数估计算法搜索精确解的整体性能,采用更多的随机数值算例来验证.令起始时间在2014-01-01—2014-01-30(1个月球周期)之间随机变化,转移时间在5~7d之间随机变化,起始点和终止点位置类似于地月自由返回轨道的边值条件,计算100个算例.在基于二体模型猜测初值的基础上,选择可调尺度参数ε为5×10－4或8×10－4,UKF参数估计算法收敛概率为98%,收敛次数在7~18次.然后,只需稍微更改尺度参数常量ε(如1×10－4),可使得余下的2%算例收敛,且具有相当的收敛次数.经过进一步的算例验证,若采用更精确的初值猜测方法,如伪状态方法,也可获得相当的收敛性能.由此可见,采用UKF参数估计算法求解三体Lambert问题的精确解具有良好的收敛性能.

6 结 论

本文提出了一种基于UKF参数估计的从初步设计到精确设计的三体Lambert问题求解方法.通过数值算例验证,该方法收敛次数较少,具有较好的鲁棒性,而且降低了对初值精确度的要求,即使利用二体模型给出的初值,也可以收敛得到精度较高的精确解,同时避免了传统数值方法对相关梯度矩阵的推导,因此显著降低了三体Lambert问题求解的难度,可以有效地解决高非线性、高敏感度的三体Lambert问题.另外,由于该方法适用于各种非线性映射的参数估计,可以在三体Lambert问题的基础上,进一步研究星际间引力辅助飞行等问题,具有广泛的应用前景.

参考文献
[1] Bate R, Mueller D,White J.Fundamentals of astrodynamics[M].New York:Dover Publications,1971:177-275.
[2] Battin R H, Vaughan R M.An elegant Lambert algorithm[J].Journal of Guidance,Control and Dynamics,1984,7(6):662-670.
Click to display the text
[3] Gooding R H. A procedure for the solution of Lambert's orbital boundary-value problem[J].Celestial Mechanics & Dynamical Astronomy,1990,48(2):145-165.
Click to display the text
[4] D'Amarion L, Byrnes D,Sackett L.Optimization of multiple flyby trajectories[C]//AAS/AIAA Astrodynamics Specialists Conference.Provincetown:AIAA Paper 1979:79-162.
Click to display the text
[5] Armellin R, Di Lizia P,Topputo F,et al.Gravity assist space pruning based on differential algebra[J].Celestial Mechanics and Dynamical Astronomy,2010,106(1):1-24.
Click to display the text
[6] Jesicak M, Ocampo C.Automated generation of symmetric lunar free-return trajectories[J].Journal of Guidance,Control and Dynamics,2011,34(1):98-106.
Click to display the text
[7] Luo Q, Yin J,Han C.Design of earth-moon free-return trajectories[J].Journal of Guidance,Control,and Dynamics,2012,36(1): 263-271.
Click to display the text
[8] Okutsu M, Longuski J.Mars free returns via gravity assist from Venus[J].Journal of Spacecraft and Rockets,2002,39(1):31-36.
Click to display the text
[9] Prado A F B A. Traveling between the Lagrangian points and the Earth[J].Acta Astronautica,1996,39(7):483-486.
Click to display the text
[10] Lian Y J, Jiang X Y,Tang G J.Halo-to-halo cost optimal transfer based on CMA-ES[C]//Proceedings of the 32nd Chinese Control Conference,CCC 2013.Piscataway,NJ:IEEE,2013:2468-2473.
Click to display the text
[11] Zazzera F B, Topputo F,Massari M.Assessment of mission design including utilization of libration points and weak stability boundaries, 18147/04/NL/mv[R].Frascati,Italy:ESA,2003.
Click to display the text
[12] Byrnes D V. Application of the pseudostate theory to the three-body Lambert problem[J].Journal of the Astronautical Sciences,1989,37:221-232.
[13] Sukhanov A, Prado A F B A.Lambert problem solution in the Hill model of motion[J].Celestial Mechanics & Dynamical Astronomy,2004,90(3):331-354.
Click to display the text
[14] 罗钦钦,韩潮. 包含引力辅助变轨的三体Lambert问题求解算法[J].北京航空航天大学学报,2013,39(5):679-687. Luo Q Q,Han C.Solution algorithm of the three-body Lambert problem with gravity assist maneuver[J].Journal of Beijing University of Aeronautics and Astronautics,2013,39(5):679-687(in Chinese).
Cited By in Cnki (3)
[15] Haykin S. Kalman filtering and neural networks[M].New York:John Wiley & Sons Inc,2002.
http://dx.doi.org/10.13700/j.bh.1001-5965.2014.0120
北京航空航天大学主办。
0

文章信息

张洪礼, 罗钦钦, 韩潮
ZHANG Hongli, LUO Qinqin, HAN Chao
UKF参数估计在三体Lambert问题中的应用
Application of UKF parameter estimation in the three-body Lambert problem
北京航空航天大学学报, 2015, 41(2): 228-233
Journal of Beijing University of Aeronautics and Astronsutics, 2015, 41(2): 228-233.
http://dx.doi.org/10.13700/j.bh.1001-5965.2014.0120

文章历史

收稿日期：2014-03-12
录用日期 : 2014-04-10
网络出版日期: 2014-05-07

相关文章

工作空间