表1(Table 1)
目前,很多学者对修理级别分析(LORA)做了大量的研究.1998年,Barros[1]提出多级多层修理级别优化模型,Barros等[2]于2001年采用分支定界法来求解该模型.2006年,Gutin等[3]提出用二分图表示Barros修理级别优化模型,提高了解的精确性,同年Saranga等[4]将智能遗传算法应用到修理级别优化模型中.2009年,Basten等[5]通过放松对决策变量的约束,将修理级别优化模型转化为最小费用流模型.2011年,Basten等[6, 7]正式采用最小费用流方法直接求解多级多站点的修理级别优化模型.
在库存优化方面,Sherbrooke[8]于1968年首次提出两层单级备件库存METRIC模型.1973年Muckstadt[9]将METRIC模型拓展为两层两级,建立了MOD-METRIC模型.1985年,Graves[10]为两层单级METRIC模型提出了一种更准确的近似估算法,即VARI-METRIC模型,而Sherbrooke[11]于1986年将此模型(VARI-METRIC)拓展为两级.1990年,Axsater[12]利用惩罚成本约束代替服务水平,为METRIC模型提出了另一种评估方法.Kim等[13]在2007年对传统多级多层库存模型中的时间分布进行拓展,提供了可修备件在一般修理时间分布下的算法.
因为修理级别分析中并不考虑基地的可用性,如果只是简单的依次考虑修理级别和备件库存,并不能得到最优的解决方案.于是,有些学者开始考虑将修理级别分析和备件库存联合优化,从而得到最优方案.1997年,Alfredsson[14]首次建立联合修理级别分析和备件库存优化的两层单级模型.2003年,Sleptchenko等[15]将维修能力考虑进来,提出有限维修能力下的修理级别和库存优化模型.2011年,Basten等[16, 17]对修理级别与库存联合优化有了深入的研究,在文献[7]的最小费用流修理级别优化模型基础上进行改进,分别采用边际分析法和迭代算法求解模型.
然而,在传统的研究中,维修时间却极少被考虑,它是影响装备系统可用度的重要参数.为了缩短维修时间,就需要存储一定数量的备件.备件库存水平的提高意味着维修时间的缩短,但同时备件配置的费用将随之增加.优化的目标是要得到费效比最佳的修理级别及库存配置数量,所以费用不可能无限地增长,备件库存水平也会受到限制.因此,为了寻找维修时间最短的送修级别,并使该时间下维修费用尽可能低,需要综合考虑维修时间和备件配置费用这两种因素.维修时间包括净维修时间和资源等待时间,净维修时间指按照具体的维修步骤,完成维修保障功能所需要的实际工作执行时间,属于固定时间;资源等待时间指保障资源配置数量有限,导致保障资源被占用而产生的等待时间,属于变化时间.在各类资源中, 等待人力人员、保障设备和保障设施的时间相当于完成故障件队列的净维修时间,维修完后即可完成等待;但等待备件时,由于备件需要跨站点运输,由备件引起的等待时间将远远长于净维修时间,也远远长于其他资源的等待时间.缩短净维修时间或其他资源等待时间相对于整个维修时间的变化并无明显效果,因此修理级别优化中令维修时间尽可能短主要通过缩短备件等待时间来实现.利用Little公式,可以将备件等待时间转化为备件短缺期望数(EBO),所以可以将维修时间-费用平衡转化为EBO-费用平衡.本文以EBO为目标函数,费用为约束条件,建立考虑维修时间的修理级别与备件库存联合优化的模型.
1 优化模型
1.1 建模分析
本文分析了单层三级保障系统,如图 1所示.
 |
| 图 1 单层三级保障结构Fig. 1 Single-indenture three-echelon support organization |
本文修理级别优化问题建立在多级保障组织的结构中,需求数、在修件数和短缺数的随机传递过程在各级保障组织间相互影响,研究这些影响关系是建模的前提(见图 2).
 |
| 图 2 LRU需求数、在修件数和短缺数的随机传递关系Fig. 2 Stochastic transitive relation of demand, in-repairing and backorder of LRU |
在保障组织各级别站点中,备件需求序列都服从均值为该站点需求率的平稳随机过程,修理级别间需求过程的传递关系通过各级别站点需求过程的数字特征相互联系.
在多级保障组织中,当有故障件到达时,故障件送至各级别维修均有一定的概率.若选择基层级进行维修,则第i个外场可更换单元(LRU)在基层级Oa站点产生的备件需求率:
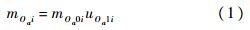
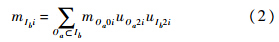
第i个LRU在基地级Dc站点的需求率:
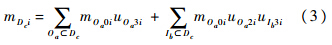
根据帕尔姆定理[18]可知,若备件的需求率服从均值为m的泊松过程,各故障件的维修周转时间为均值T,且分布相互独立,则在修件数服从均值为mT的泊松分布.
第i个LRU在基层级Oa站点的在修件期望数:
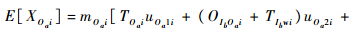
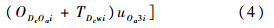
第i个LRU在中继级Ib站点的在修件期望数:
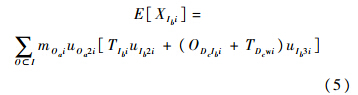
第i个LRU在基地级Dc站点的在修件期望数:
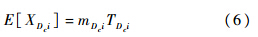
需求到达后,高级别站点将对提出LRU需求的低级别站点进行补给,若该站点库存不足,则出现短缺.
第i个LRU在基层级Oa站点的备件期望短缺数:
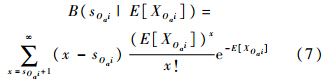
第i个LRU在中继级Ib站点的备件期望短缺数:
第i个LRU在基地级Dc站点的备件期望短缺数:
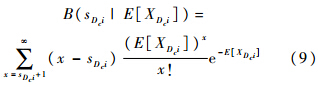
修理级别优化问题关注的是基层级的备件等待时间,根据Little公式,平均等待备件时间可以通过期望备件短缺数EBO除以备件需求率计算得出,即
1.2 目标函数及建模条件
本文主要是考虑维修时间的修理级别与库存联合优化,要权衡维修时间(主要是备件等待时间)和费用之间的关系.在引言中,已经分析了本模型的目标函数是EBO,而EBO是由备件等待时间转化而来的.因此优化模型的实际目标函数是备件的平均等待时间.现推导以目标函数为前提的平均等待时间与EBO之间的关系.
在多级保障组织中,平均等待时间是指基层级各站点平均等待时间按各自需求率加权的平均值,如式(11):
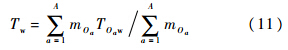
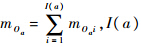为第i个LRU在基层级Oa站点的种类数;TOaw为基层级Oa站点的平均等待时间,同理可利用式(11)由该站点各类LRU平均等待时间计算而得.根据式(10),可得
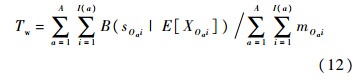
由式(12)可知,当需求率已知时,令平均等待时间Tw最小相当于令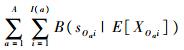
最小,即为本模型目标函数.
本模型的维修活动在以下条件下进行:
1) LRU故障时间服从指数分布;
2) 库存策略为可修产品的及时送修策略——(s-1,s)策略;
3) 除备件外,其他维修资源均供应充足且维修都是成功的.
1.3 多级优化模型
经引言分析,本优化模型的约束条件需要考虑维修费用和决策变量两类约束.
维修费用包括资源费用和备件费用.在资源费用方面,由于假设维修都是成功的,使得维持维修能力所需的资源费用也为固定值,无优化效果.在建立关于费用约束的不等式时,从费用上限中可以将此部分费用略去,费用不等式方程两边也不会受到影响.在备件费用方面,按模型的中间变量,即库存配置数量计算备件配置的总费用.将维修费用限定在一定范围内,构造维修费用的约束式,如式(13):
在决策变量约束方面,包含3部分内容:①由于优化建模要得出的是确定的修理级别,所以各变量均为0-1变量,1表示在该站点维修,0表示不在该站点维修,这部分约束如式(14)所示;②对故障LRU,只能送往基层级、中继级和基地级中的某一个级别,如式(15)所示;③当故障LRU被送往中继级维修时,可选择在中继级本地维修,也可选择送往基地级维修,如式(16)所示.
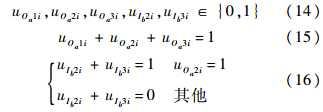
令
为目标函数,式(13)~式(16)为约束条件,建立多级保障组织单层产品情况下的修理级别优化模型,如式(17)所示.
综上,本模型可以表示为
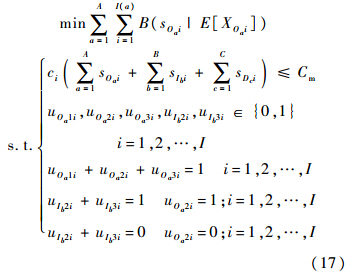
2 优化算法 2.1 优化目标函数 B(s,u) 分析
相对于传统METRIC模型中目标函数B(s),本文引入送修决策变量 u后,期望备件短缺数函数不再以库存为唯一变量,而是以库存数s和送修级别u为变量的二维变量函数B(s,u ).尽管EBO在库存维表现出凸函数特性,但在送修级别维的函数性质并不明确.
下面选择三级保障组织单项备件为对象,验证B( u )的函数特性.
设各级修理级别仅有一个站点,LRU送往基层级、中继级和基地级维修的概率向量为 u ={u1,u2,u3},且均为0-1变量.设各级别站点备件库存数为0,则期望短缺数与该站点的需求数相等,3种取值下基层级期望短缺数分别为
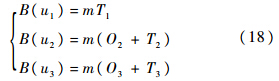
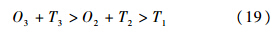
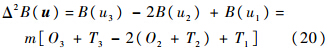
调整站点间的距离或定义适当的维修时间,都能使Δ2 B( u )<0同时满足式(19),因此 B( u)为非凸函数.按照凸优化算法的原理,以库存数s和送修级别组合 u 为变量的二维变量函数B(s,u )在实施凸优化算法时需要对库存数和送修级别分别进行遍历.B( u )为非凸函数,说明加入送修级别变量后,优化问题的寻优路径受到了影响,进而影响到凸优化算法的应用,需要对函数进行重构或对算法进行改进.
2.2 算法分析
由于对各类备件的送修级别组合进行遍历时,送修级别组合循环嵌套在备件种类循环内,所以,若在遍历备件种类之前,已按送修级别决策变量构造出各类备件的EBO凸曲线,则各类备件按其单位费用效应边际量迭代可以进行凸优化.因此,解决非凸函数优化算法的关键在于:为各类备件以送修级别为唯一变量的非凸函数 B( u )分别构造凸函数.
构造每类备件的修理级别凸函数的过程与构造 B( u )-C 费用优化曲线的方法相同,也是利用增加该类备件产生的单位费用效应进行寻优决策.对于某一类备件,可能有多种送修级别可供选择,此时相当于固定 B(s,u )中的库存s,比较哪种选择产生的B( u )最小,在追加备件库存的每一步都选择产生最小B( u )的送修级别,则可产生最优的B( u )-C 凸曲线.
用 B( u )-C 凸曲线上的点进行各类备件间的优化分析,得到的将是 B(s,u )-C 最优曲线.采用边际分析法,生成 B(s,u )-C 费用最优曲线.算法步骤如下:
步骤1 初始化库存数量si=0,i;
步骤2 获取各类备件在各站点的送修级别以及在各站点的EBO;
步骤3 构造各类备件在送修组合下的凸曲线;
步骤4 对各类备件凸曲线上的数据计算EBO-费用的边际效应值Δ;
步骤5 选择Δ最高的备件和修理级别配置备件;
步骤6 检查是否超出费用约束,若未超出,返回步骤2,否则停止.
3 应用案例
本文示例以装备的维修规划为背景,介绍针 对关键LRU部件,如何按照本文提出的修理级别优化理论,应用凸规划优化算法,进行保障系统修理级别分析、建模、求解和验证工作.
在本案例中,建立如图 1所示的单层三级优化模型.一个基地级有两个中继级(I1和I2),每个中继级有两个基层级(O1,O2和O3,O4).在每个基层级部署10个系统,每个系统由4类LRU组成.考虑到每个站点所处环境不同、系统使用情况不同,故同类LRU在不同站点需求率不同,不同站点维修能力不同(修理时间).利用Simlox软件对4个基层级的40个系统执行1年任务进行仿真验证,输入数据如表 1所示.
| LRUi | mOai/次 | TDci/h | TIbi/h | TOai/h | ODcIbi/h | ODcOai/h | OIbOai/h | ci/万元 | Cm/万元 |
| LRU1 | 110.9 | 17.5 | 30.2 | 30.7 | 33.4 | 37.7 | 33.3 | 4 | 100 |
| 162.2 | 17.5 | 30.2 | 35.9 | 33.4 | 42.9 | 27.2 | 4 | ||
| 113.5 | 17.5 | 12.9 | 59.6 | 34.5 | 40.3 | 26.3 | 4 | ||
| 161.9 | 17.5 | 12.9 | 41.2 | 34.5 | 40.3 | 33.3 | 4 | ||
| LRU2 | 149.9 | 17.5 | 26.0 | 56.1 | 33.4 | 37.7 | 33.3 | 4 | |
| 115.2 | 17.5 | 26.0 | 52.6 | 33.4 | 42.9 | 27.2 | 4 | ||
| 153.8 | 17.5 | 27.3 | 35.9 | 34.5 | 40.3 | 26.3 | 4 | ||
| 107.2 | 17.5 | 27.3 | 50.8 | 34.5 | 40.3 | 33.3 | 4 | ||
| LRU3 | 134.1 | 17.5 | 20.3 | 53.4 | 33.4 | 37.7 | 33.3 | 6 | |
| 149.7 | 17.5 | 20.3 | 42.0 | 33.4 | 42.9 | 27.2 | 6 | ||
| 134.6 | 17.5 | 16.0 | 49.1 | 34.5 | 40.3 | 26.3 | 6 | ||
| 118.4 | 17.5 | 16.0 | 59.6 | 34.5 | 40.3 | 33.3 | 6 | ||
| LRU4 | 161.8 | 17.5 | 28.5 | 43.8 | 33.4 | 37.7 | 33.3 | 6 | |
| 120.3 | 17.5 | 28.5 | 45.6 | 33.4 | 42.9 | 27.2 | 6 | ||
| 125.8 | 17.5 | 30.9 | 55.2 | 34.5 | 40.3 | 26.3 | 6 | ||
| 133.1 | 17.5 | 30.9 | 33.3 | 34.5 | 40.3 | 33.3 | 6 |
输出结果:费用约束是100万元;目标函数EBO优化值为2.3.最优修理级别如表 2所示.
| 站点 | 故障件 | 送修级别 | |
| 中继级I1 | 基层级O1 | LRU1 | 本地O1 |
| LRU2 | 基地级 | ||
| LRU3 | 本地O1 | ||
| LRU4 | 本地O1 | ||
| 基层级O2 | LRU1 | 本地O2 | |
| LRU2 | 本地O2 | ||
| LRU3 | 本地O2 | ||
| LRU4 | 本地O2 | ||
| 中继级I2 | 基层级O3 | LRU1 | 中继级I2 |
| LRU2 | 本地O3 | ||
| LRU3 | 中继级I2 | ||
| LRU4 | 本地O3 | ||
| 基层级O4 | LRU1 | 本地O4 | |
| LRU2 | 本地O4 | ||
| LRU3 | 中继级I2 | ||
| LRU4 | 本地O4 | ||
LRU在各级站点的最优库存配置如表 3所示.
| LRUi | >基地级 | 中继级 | 基层级 | ||||
| I1 | I2 | O1 | O2 | O3 | O4 | ||
| LRU1 | 0 | 0 | 0 | 1 | 2 | 1 | 2 |
| LRU2 | 0 | 0 | 0 | 2 | 2 | 2 | 1 |
| LRU3 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| LRU4 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
如图 3所示为EBOi-C曲线和EBO-C曲线.
 |
| 图 3 各类LRU优化曲线Fig. 3 Optimal curves of each LRU |
从图 3中可以看出4类LRU在总费用约束下分别得出的EBO优化曲线,在图 4中展示了4类LRU的综合EBO优化曲线.在图 5中,以表 1的数据、表 2的最优修理级别和表 3的库存配置作为仿真输入,利用Simlox软件,对利用本文所提出算法及模型算出的EBO进行仿真验证,可以得出仿真EBO为2.7,而理论计算值为2.3,两者之间相差很近,即可证明本文算法的正确性.
 |
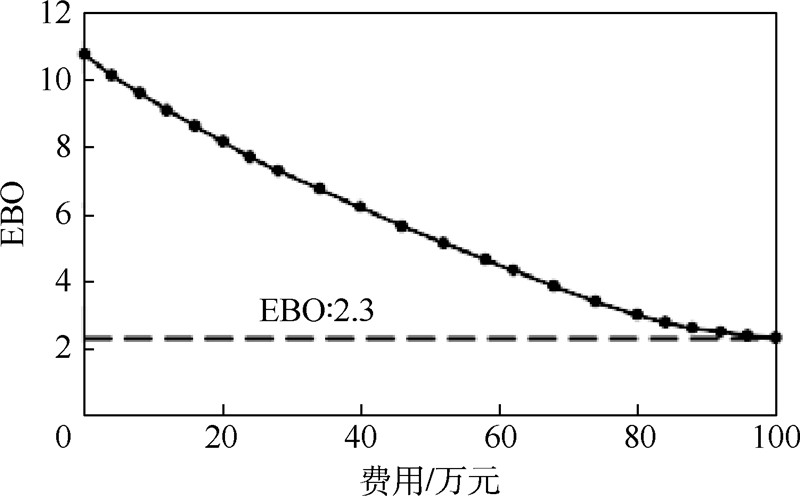| 图 4 多类LRU综合优化曲线Fig. 4 Comprehensive optimal curve of multi-type LRU |
 |
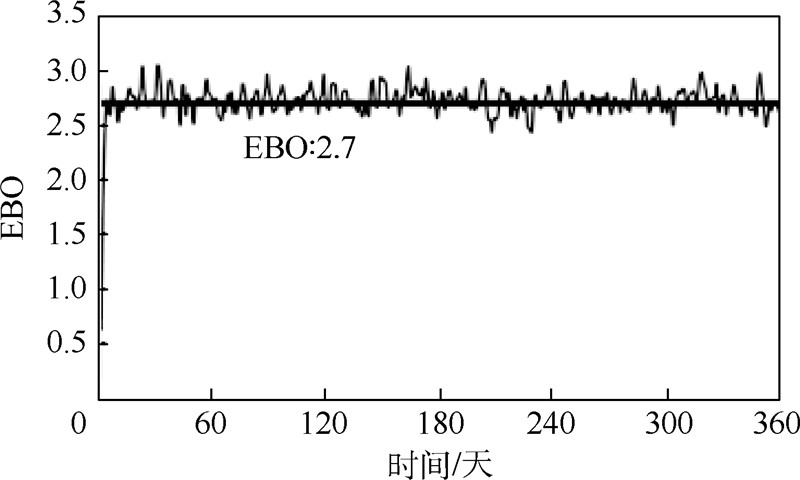| 图 5 多类LRU优化和仿真曲线Fig. 5 Optimization and simulation curve of multi-type LRU |
本文提出了一种在复杂装备保障系统中重点考虑维修效能的修理级别分析方法,建立了备件库存与修理级别分析联合优化模型.
1) 根据本文所提出模型和算法，能够对复杂装备保障系统中的修理级别和备件进行优化.
2) 本文所设计的多变量凸优化算法能够解决大规模站点群数量和备件数量的循环嵌套运算.
3) 利用本模型所得出的最优修理级别和库存配置,通过Simlox软件仿真,比较目标函数值EBO的仿真和理论计算结果,证明了本文所提出的模型和算法的正确性.
下一步的工作将着眼于考虑更多的维修资源以及资源相关性,建立有限维修能力的优化模型.
| [1] | Barros L L. The optimization of repair decisions using life-cycle cost parameters[J].IMA Journal of Mathematics Applied in Business & Industry,1998,9(4):403-413. |
| [2] | Barros L L, Riley M.A combinatorial approach to level of repair analysis[J].European Journal of Operational Research,2001,129(2):242-251. |
| Click to display the text | |
| [3] | Gutin G, Rafiey A,Yeo A,et al.Level of repair analysis and minimum cost homeomorphisms of graphs[J].Discrete Applied Mathematics,2006,154(6):881-889. |
| Click to display the text | |
| [4] | Saranga H, Kumar U D.Optimization of aircraft maintenance/support infrastructure using genetic algorithm-level of repair analysis[J].Annals of Operations Research,2006,143(1):91-106. |
| Click to display the text | |
| [5] | Basten R J I, Schutten J M J,Heijden M C.An efficient model formulation for level of repair analysis[J].Annals of Operations Research,2009,172(1):119-142. |
| Click to display the text | |
| [6] | Basten R J I, Heijden M C,Schutten J M J.An efficient model formulation for level of repair analysis[J].Annals of Operation Research,2009,172(1):119-142. |
| Click to display the text | |
| [7] | Basten R J I, Van der Heijden M C,Schutten J M J.A minimum cost flow model for level of repair analysis[J].International Journal of Production Economics,2011,133(1):233-242. |
| Click to display the text | |
| [8] | Sherbrooke C C. METRIC:a multi-echelon technique for recoverable item control [J].Operations Research,1968,16(1):122-141. |
| Click to display the text | |
| [9] | Muckstadt J A. A model for a multi-item,multi-echelon,multi-indenture inventory system[J],Management Science,1973,20(4): 472-481. |
| [10] | Graves S C. A multi-echelon inventory model for a repairable item with one-for-one replenishment[J].Management Science,1985,20(4):472-481. |
| [11] | Sherbrooke C C. VARI-METRIC:improved approximations for recoverable item control[J].Operations Research,1986,34(2): 311-319. |
| Click to display the text | |
| [12] | Axsater S. Simple solution procedures for a class of two-echelon inventory problem[J].Operations Research,1990,38(1):64- 69. |
| Click to display the text | |
| [13] | Kim J S, Shin K C,Park S K.An algorithm for repairable item inventory system with depot spares and general repair time distribution[J].Applied Mathematical Modelling,2007,31(5):795-804. |
| Click to display the text | |
| [14] | Alfredsson P. Optimization of multi-echelon repairable item inventory system with simultaneous location of repair facilities[J].European Journal of Operational Research,1997,99(3):584-595. |
| Click to display the text | |
| [15] | Sleptchenko A, Heijden M C,Harten A.Trade-off between inventory and repair capacity in spare part networks[J].Journal of the Operations Research Society,2003,54(3):263-272. |
| Click to display the text | |
| [16] | Basten R J I, Van der Heijden M C,Schutten J M J.Practical extensions to a minimum cost flow model for level of repair analysis[J].European Journal of Operational Research,2011,211(2):333-342. |
| Click to display the text | |
| [17] | Basten R J I, Heijden M C,Schutten J M J.Joint optimization of level of repair analysis and spare stocks[J].European Journal of Operational Research,2012,222(3):474-483. |
| Click to display the text | |
| [18] | Sherbrook C C. Optimal inventory modeling of systems:multi-echelon techniques[M].2rd ed.New York:Kluwer Academic Publishers,2004:22-22.. |
