Download PDF  
文章快速检索  
  高级检索
引用本文
王伟, 刘立冬, 王刚, 贠超. 基于四元数表示法的机器人基坐标系标定方法[J]. 北京航空航天大学学报, 2015, 41(3): 411-417
WANG Wei, LIU Lidong, WANG Gang, YUN Chao. Calibration method of robot base frame by quaternion form[J]. Journal of Beijing University of Aeronautics and Astronsutics, 2015, 41(3): 411-417.
基于四元数表示法的机器人基坐标系标定方法
王伟, 刘立冬, 王刚, 贠超    
北京航空航天大学 机械工程及自动化学院, 北京 100191
收稿日期: 2014-04-30; 录用日期: 2014-06-12; 网络出版时间：2014-12-09
基金项目：北京航空航天大学基本科研业务费资助项目(YWF-14-JXXY-016); 高等学校博士学科点专项科研基金资助项目(20121102120020).
通讯作者: 王伟（1982—），男，湖北京山人，讲师，jwwx@me.buaa.edu.cn，主要研究方向为机器人学.
摘要：在多机器人协同、运动学参数辨识和机器人离线编程等作业任务下,需要标定出机器人基坐标系在世界坐标系中的精确位姿.提出和实施了一种利用四元数表示法进行机器人基坐标系精确标定的方法.利用指数积公式,建立机器人的运动学模型.利用外部测量设备,测量出5个不共面的工具中心点,并记录对应的机器人关节位形.以基坐标系位姿对应的旋转矩阵元素为变量,建立不相容方程组,并求出基坐标系位姿的初步齐次矩阵.由于测量误差和截断误差,初步齐次矩阵的旋转矩阵部分不能满足单位正交阵的性质.利用四元数的几何约束条件,建立罚函数形式的目标方程,将初步齐次矩阵进行正交化修正.通过一系列的实际机器人的标定试验,验证了该标定方法的正确性,并提高了机器人末端的定位精度.
关键词： 机器人     标定     基坐标系     四元数     正交性    
Calibration method of robot base frame by quaternion form
WANG Wei , LIU Lidong, WANG Gang, YUN Chao     
School of Mechanical Engineering and Automation, Beijing University of Aeronautics and Astronautics, Beijing 100191, China
Abstract:The accuracy pose of robot base frame with respect to the world frame needs to be calibrated under the task of multi-arm cooperation, identification of kinematics parameter and off-line program of robot. An accurately calibration method of robot base frame using quaternion form was proposed and applied. The kinematic model of robot was established by the product-of-exponential formula. 5 tool center points (TCPs), which were not coplanar, were measured with the external measuring device, and the corresponding robot joint configurations were also recorded. By considering the elements of rotational matrix corresponding to the base frame pose as the variables, a group of incompatible equations was set up, and the initial homogeneous matrix of the base frame pose was also obtained. However, due to the errors of measuring and truncation, the rotational matrix part of initial homogeneous matrix cannot satisfy the regulation of unit orthogonal matrix. Using the geometrical constraints of a quaternion, an objective equation by the form of penalty function was established, and the initial homogeneous matrix was orthogonalized. By a set of practical calibration experiments of robot, the validity of calibration method was verified, which improved the accuracy of the location of robot end.
Key words: robot     calibration     base frame     quaternion     orthogonality    

工业机器人具有较大的灵活工作空间和较高的重复定位精度,已经被广泛应用在自动化生产中.为了满足更加精细的作业需求,如何进一步提高工业机器人的定位精度是当前的研究热点之一.标定工业机器人的基坐标系是提高机器人定位精度的有效手段之一.机器人基坐标系一般设置在机器人底座的固定位置,当第1关节转角为0时,基坐标系与第1连杆坐标系重合.通常需要利用标定方法才能获得机器人基坐标系在世界坐标系中的精确位姿.精确标定机器人基坐标系,在机器人离线编程[1]、多机器人协调[2]和机器人控制[3]等领域具有重要的意义.

Haytti模型[4]、CPC模型[5]、S模型[6]和指数积模型[7]等被广泛应用于机器人运动学参数的标定,而有关机器人基坐标系标定的研究则较少.

目前国内外有关机器人基坐标系标定的研究成果可分为:快速标定和精细标定.快速标定适用于工业现场的机器人基坐标的简便标定.快速标定技术方法可分为3类.

第1类是采用球面、圆柱面和平面等特殊几何形状[8, 9].利用机器人末端与特殊几何形状接触,从而将开链机器人转化为闭链结构,根据不同接触位形建立非线性不相容方程组,求解该方程组的最小二乘解,实现机器人基坐标系的标定.

第2类采用线性位移传感器等增量式测量设备.文献[10]集成了线性位移传感器,提出了一种“相对标定”的想法.这种标定方法包括的标定步骤多,包括的误差因素较多.

第3类采用单目或双目视觉标定技术[11, 12],其数学模型与第1类标定方法相同.视觉标定不需要实际的物理接触,测量范围更大,有利于提高最终的标定精度,但是摄像头本身的精确度会影响标定结果.

精细标定往往需要采用外部的精确测量设备,并设计相应的离线标定算法.典型的测量设备为激光跟踪仪[13]、三维坐标测量机和被动式机器人测量臂[14]等.精细标定方法的周期较长,一般适用于离线场合.文献[15]利用瞬时轴法标定了双臂协调机器人的基坐标系,提高了旋转矩阵的正交性.文献[16]对不精确的旋转矩阵做奇异值分解,获得了接近于单位齐次矩阵的真实旋转矩阵.

本文采用四元数表示法来提高机器人基坐标系的旋转矩阵的正交性.本文建立了机器人运动学模型,设计了基坐标系的初始标定方法,提出了四元数表示法的基坐标系的精确标定方法,完成了标定试验,对比了标定前后机器人的精度. 1 运动学建模

选定{S}为机器人基坐标系,工具坐标系{T}与末端被测点坐标系重合.当机器人的全部关节转角都处于理论零位,即q={0}时,{S}和{T}之间的刚体位移定义为参考位形gst(0).

对于每一个关节,构造一个螺旋ξi.对于转动关节,关节螺旋ξi=[vi ωi]T,vi=－ωi×Oi,ωi∈R3是关节轴线方向上的单位矢量,Oi∈R3为轴线上的任一点.对于移动关节,关节螺旋ξi=[vi0]T,vi∈R3是指向移动方向的单位矢量.

利用指数积公式将各关节的运动加以组合,可得n个关节的串联机器人正向运动学方程:

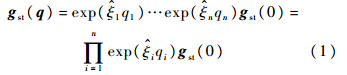
往往测量坐标系{M}与机器人基坐标系{S}不重合,后者相对于前者存在一个刚体位移gms.在测量坐标系{M}下描述的机器人正运动学方程为

2 基坐标系初始标定

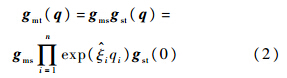
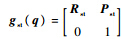设末端相对于测量坐标系的位姿gmt(q)=,基坐标系相对于测量坐标系的位姿gms=,末端相对于基坐标系的位姿.利用矩阵的分块乘法,由式(2),有

设
由式(3),依次做4次减法可得
Rms包括9个未知数,式(4)可以分解为12个独立方程,那么式(4)为不相容方程组.对式(4)两端做转置,可得
令
令

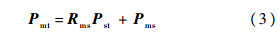
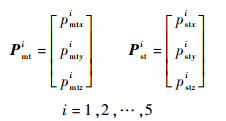
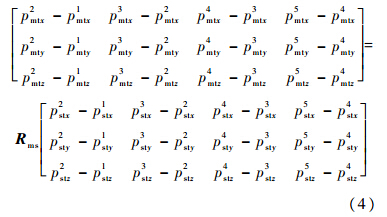
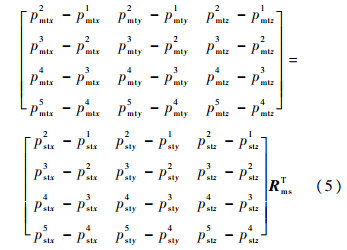
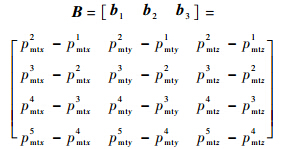
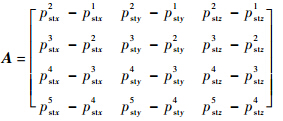
令RmsT=[x1 x2 x3],则由式(5)可得

式中,bi和A为已知量;xi为待求量.

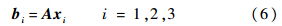
建立不相容方程组,可得

由于A为列满秩,可得

由式(7),可以求得Rms的3个列向量,以确定基坐标系相对于测量坐标系的姿态.由式(3)可得

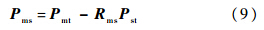
利用式(9)即可求得Pmt,从而确定基坐标系相对于测量坐标系的位置.由式(7)和式(9)可以完成基坐标系的初步标定. 3 基坐标系精细标定

利用上述初步标定方法,可以获得基坐标系的初步位姿g′ms(q).但是由于测量误差和计算截断误差的存在,导致g′ms(q)中的旋转矩阵不能满足单位矩阵的正交性.在基坐标系精细标定中,利用四元数表示法来解决旋转矩阵的正交性. 3.1 单位四元数表示法

描述两坐标系之间的姿态可以用3个独立元素来描述.单位四元数是一种描述两个正交坐标系之间的相对姿态的数学表示法.单位四元数仅需要4个元素,需满足一个约束条件.而旋转矩阵包括9个元素,则需满足6个约束条件.相对而言,四元数表示法比旋转矩阵更加简洁,且二者之间存在等效变换关系.

若存在四元数q,设为q=q0+iq1+jq2+kq3,令q=iq1+jq2+kq3,那么

设与之对应的旋转矩阵为R,那么由关节螺旋定义可得

利用Rodrigue公式[17],可得

式中

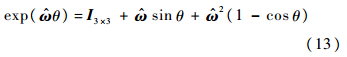
将式(10)、式(11)和式(13)代入式(12),可得

式中

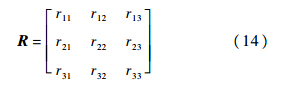
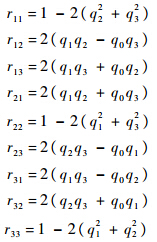
3.2 旋转矩阵的优化

利用式(7)标定所得的初步旋转矩阵不能满足旋转矩阵的正交性,因此需要优化初步标定结果.旋转矩阵优化就是定义一个目标函数,当四元数变量取得最优值时,目标函数取极小值.

设与q等效的旋转矩阵为R,令R=Rot(q0,q1,q2,q3).定义R与Rmt之间的距离函数为

其中F表示为矩阵的F范数.选定上述距离函数为优化目标函数C,则

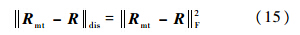
当R为正交化结果时,应满足以下方程:

那么
且满足:

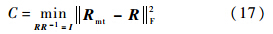
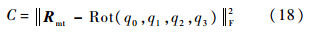
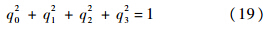
方程(18)可视为一个数学优化问题,即求得多变量函数C的最小值,并且满足约束条件q02+q12+q22+q32=1.拉格朗日乘子法为该类优化问题提供了有效的求解方法.定义拉格朗日方程如下:

设

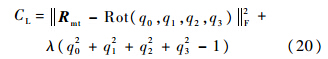
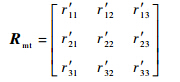
则式(20)可化为

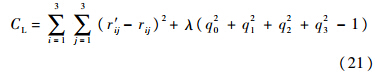
将式(14)代入式(21),可得

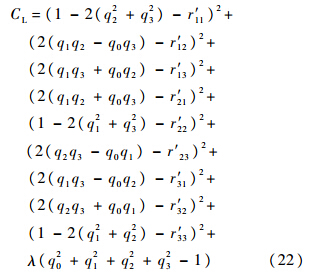
当式(22)取得极值时,满足以下非线性方程组:

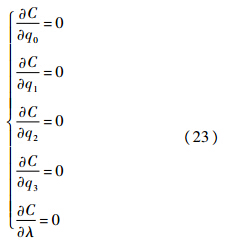
列出上述方程组的显示表达式为

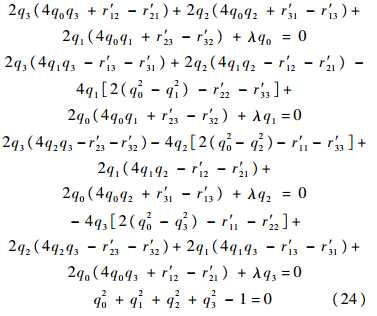
式(24)为非线性方程组,包括5个变量和5个方程.利用牛顿迭代法即可求出式(24)的数值解[q0O q1O q2O q3O λO].

当q*=[q0O q1O q2O q3O]取得该数值解时,其对应的旋转矩阵与初步标定的旋转矩阵距离最近,从而实现旋转矩阵的精细标定. 4 标定试验

本节介绍机器人基坐标系标定的试验系统组成、标定步骤、标定数据和标定前后机器人精度对比. 4.1 标定试验系统

在运动学参数标定试验中,试验系统由FARO ARM、末端球形靶标和ABB公司的标准工业机器人IRB 1410组成,如图 1所示.图 1中{T}表示待测量的靶标坐标中心,视为工具坐标系.{S}为IRB 1410机器人的基坐标系,{M}为FARO ARM的测量坐标系.IRB1410机器人的自由度数为6,其几何参数的名义值为:l1=170 mm;l2=475 mm;l3=600 mm;l4=1 195 mm;l5=720 mm.在{S}下,靶标相对于机器人手腕中心的位置偏移量为(-14.17 mm,-12.10 mm,251.39 mm).

图 1 机器人基坐标系标定系统原理图Fig. 1 Schematic of robot base frame calibration system
图选项
4.2 试验步骤和数据

在图 1所述标定系统中,FARO ARM可以直接测量出靶标中心{T}在{M}下的位置坐标.读取IRB 1410的关节转角,利用式(1),可以获得靶标中心{T}在{S}下的名义位置.而在一次测量中,{S}与{M}之间存在一个固定的刚体变换gms.假设机器人运动学参数无误差,利用四元数表示法即可精确标定出gms的实际值.从而将测量所得位置坐标和名义位置坐标转换到同一个坐标系{M}中.

考虑到FARO ARM测量臂的测量范围较小,本次测量一共设计20个测量点.每个测量点对应一个不同的机器人关节位形.实际测量过程如图 2 所示.一共测量20个不同的末端位置,3个坐标分量记为{PxPyPz}T,如表 1所示,p为末端位置序号.对应的机器人关节位形q,如表 2所示.

图 2 末端坐标测量Fig. 2 Coordinate measurement of end
图选项
表 1 末端位置坐标Table 1 Position coordinates of endmm
pPxPyPz
1-460.890 1549.517 5-27.609 1
2-362.291 9390.865 8-53.967 2
3-296.550 1231.185 4-85.149 6
4-260.442 278.538 5-119.147 9
5-463.434 9458.011 5-136.617 8
6-238.384 0167.067 7-201.002 5
7-218.092 97.843 2-238.375 4
8-207.299 7158.385 2-184.361 8
9-392.060 1406.649 7-239.146 6
10-331.767 6249.871 2-281.312 5
11-308.002 4101.785 4-318.316 2
12-160.459 294.983 5-311.768 5
13-294.703 1185.589 5-402.290 9
14-306.393 9349.437 7-346.226 6
15-263.037 1184.986 8-388.513 1
16-241.509 429.029 0-429.597 9
17-408.238 0265.099 1-456.836 2
18-430.845 4420.156 7-401.901 6
19-231.475 4120.404 1-523.064 6
20-232.738 0-42.431 6-558.272 0
表选项
表 2 机器人关节位形Table 2 Robot’s joint configurations
pq/(°)
1 -10.000,25.000,-40.00,-40.000,95.000,-160.000
2-10.000,30.000,-30.00,-30.000,100.000,-155.000
3-10.000,35.000,-20.00,-20.000,105.000,-150.000
4-10.000,40.000,-10.00,-10.000,110.000,-145.000
5-5.000,25.000,-35.000,-35.000,110.000,-140.000
6-5.000,35.000,-15.00,-15.000,95.000,-155.000
7-5.000,40.000,-5.000,-5.000,100.000,-150.000
8-5.000,45.000,-20.000,-20.000,105.000,-145.000
90.000,25.000,-30.000,-30.000,100.000,-145.000
100.000,30.000,-20.000,-20.000,105.000,-140.000
110.000,35.000,-10.000,-10.000,110.000,-160.000
120.000,45.000,-15.000,-15.000,95.000,-150.000
135.000,30.000,-15.000,-15.000,95.000,-145.000
145.000,35.000,-30.000,-30.000,100.000,-140.000
155.000,40.000,-20.000,-20.000,105.000,-160.000
165.000,45.000,-10.000,-10.000,110.000,-155.000
1710.000,25.000,-20.000,-20.000,105.000,-155.000
1810.000,30.000,-35.000,-35.000,110.000,-150.000
1910.000,40.000,-15.000,-15.000,95.000,-140.000
2010.000,45.000,-5.000,-5.000,100.000,-160.000
表选项
4.3 标定结果

本节分别利用非线性最小二乘拟合、初步标定和精细标定等3种方法对试验系统中的IRB 1410机器人的基坐标系进行标定,并验证标定后的机器人末端的精度水平.

1) 非线性最小二乘拟合.

将式(3)按行转化为3个非线性方程.每个方程包括4个未知数.分别取5个测量位形,采用最小二乘非线性拟合方法,即可求出4个未知数.所选取的5个测量位形的序号分别是:4,8,11,14,17,标定所得的基坐标系位姿矩阵为

2) 初步标定.

利用式(7)和式(9),即可求出初始标定的基坐标系位姿.所选取的5个测量位形的序号分别是:4,8,11,14,17,标定所得的基坐标系位姿矩阵为

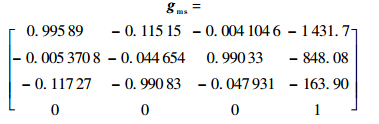
3) 精细标定.

利用式(24),即可求出精细标定的基坐标系位姿.所选取的5个测量位形的序号分别是:4,8,11,14,17,标定所得的基坐标系位姿矩阵的四元数为q*=[0.689 19－0.722 240.041 4050.040 907]对应的齐次矩阵为

4) 标定结果对比.

分别利用最小二乘法拟合标定结果、初始标定结果和精细标定结果,对4.2节中的20组机器人位形和对应的末端位置进行精度验证.验证结果如图 3所示,其中纵坐标为所测点的名义坐标与测量坐标之间的绝对定位误差,横坐标是所测点的序号.

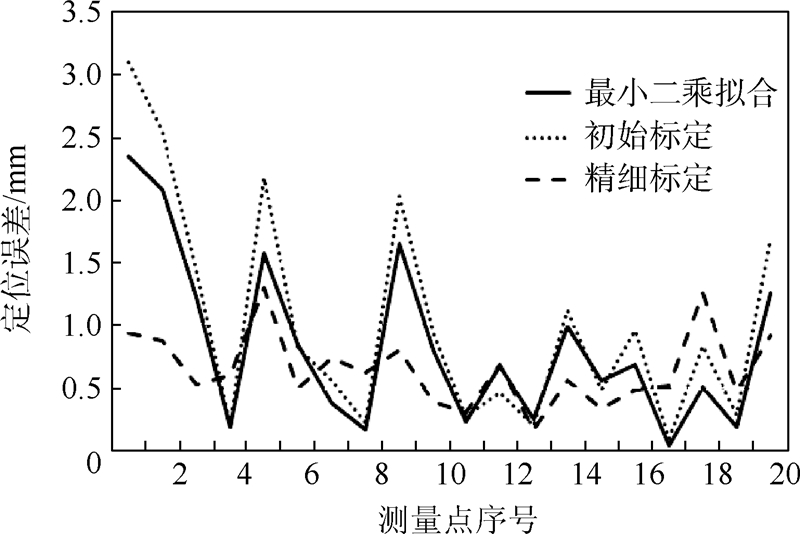图 3 精度验证和比较Fig. 3 Verification and comparation of accuracy
图选项

如果采用最小二乘拟合法对机器人基坐标系进行标定,那么第1点处误差最大,定位偏差为2.35 mm,在第17点处误差最小,定位偏差为0.045 mm.

如果采用初始标定的机器人基坐标系位姿,那么第1点处误差最大,定位偏差为3.09 mm,在第17点处误差最小,定位偏差为0.099 mm.

如果采用本文的精细标定方法,那么在第5点处误差最大,定位偏差为1.30 mm,在第13点处误差最小,其定位偏差为0.165 mm.

可见,经过基坐标系的精细标定后,所测20个位置的定位误差带缩小,各点的定位误差更加均匀,提高了机器人的定位精度.

5 结 论

本文提出和实施了一种采用四元数表示法的机器人基坐标系的精确标定方法,提高了基坐标系姿态矩阵的正交性.

1) 初始标定步骤中,建立待标定齐次矩阵的不相容非线性方程组,以最小二乘解作为初始标定结果.

2) 在精细标定中,采用了四元数法来描述机器人基坐标系的实际位姿,以初始标定位姿与实际位姿偏差矩阵的F范数为优化目标方程,采用拉格朗日乘子法和牛顿迭代法获得机器人基坐标系的精确标定结果.

3) 搭建了工业机器人和测量臂组成的标定试验系统,完成20个测量点的验证试验,证明经过本方法标定后,最大机器人定位误差减小为1.30 mm.

参考文献
[1] Jin X S, Yang X C.Off-line programming of a robot for laser re-manufacturing[J].Tsinghua Science & Technology,2009,14(S1): 186-191.
Click to display the text
[2] Pradeep V, Konolige K,Berger E.Calibrating a multi-arm multi-sensor robot:a bundle adjustment approach[J].Experimental Robotics Springer Tracts in Advanced Robotics,2014,79:211-225.
Click to display the text
[3] Graig J J. Introduction to robotics:mechanics and control[M].3rd ed.Upper Saddle River:Pearson Education Inc,2005:10-20.
[4] Hayati S A. Robot arm geometric link parameter estimation[C]//Proceedings of 22nd IEEE Conference on Decision and Control.San Antonio,Texas:IEEE,1983,22:1477-1483.
Click to display the text
[5] Zhuang H, Roth Z S,Hamano F.A complete and parametrically continuous kinematic model for robot manipulators[J].IEEE Transactions on Robotics and Automation,1992,8(4):451-463.
Click to display the text
[6] Stone H W, Sanferson A C.A prototype arm signature identification system[J].Proceeding of IEEE Conference on Robotics and Automation,1987,4:175-182.
Click to display the text
[7] He R, Zhao Y J,Yang S N,et al.Kinematic-parameter identification for serial-robot calibration based on POE formula[J].IEEE Transactions on Robotics,2010,26(3):411-423.
Click to display the text
[8] Gan Z, Rossano G,Li X,et al.Method for calibrating and programming of a robot application:US,Patent 6,822,412[P].2004-11-23.
Click to display the text
[9] Gu X, Feng C.A calibration procedure for a system of two coordinated manipulators[J].International Journal of Robotics and Automation,1995,10(4):152-158.
[10] Sun Y, Giblin D J,Kazerounian K.Accurate robotic belt grinding of workpieces with complex geometries using relative calibration techniques[J].Robotics and Computer-Integrated Manufacturing,2009,25(1):204-210.
Click to display the text
[11] Jianbo S U. Base calibration for dual robot system[J].Control Theory and Applications,1998,15(4):575-582.
Click to display the text
[12] Wang H, Shen S,Lu X.A screw axis identification method for serial robot calibration based on the POE model[J].Industrial Robot:An International Journal,2009,39(2):146-153.
Click to display the text
[13] Nubiola A, Bonev I A.Absolute calibration of an ABB IRB 1600 robot using a laser tracker[J].Robotics and Computer-Integrated Manufacturing,2013,29(1):236-245.
Click to display the text
[14] Santolaria J, Aguilar J J,Yanue J A,et al.Kinematic parameter estimation technique for calibration and repeatability improvement of articulated arm coordinate measuring machines[J].Precision Engineering,2008,32(4):251-268.
Click to display the text
[15] Gan Y, Dai X.Base frame calibration for coordinated industrial robots[J].Robotics and Autonomous systems,2011,59(7):563-570.
Click to display the text
[16] Ernst F, Richter L,Mmtthaus L,et al.Non-orthogonal tool/flange and robot/world calibration[J].The International Journal of Medical Robotics and Computer Assisted Surgery,2012,8(4): 407-420.
Click to display the text
[17] Murray R M, Li Z,Sastry S S,et al.A mathematical introduction to robotic manipulation[M].Boca Raton:CRC Press,1994:28.
http://dx.doi.org/10.13700/j.bh.1001-5965.2014.0239
北京航空航天大学主办。
0

文章信息

王伟, 刘立冬, 王刚, 贠超
WANG Wei, LIU Lidong, WANG Gang, YUN Chao
基于四元数表示法的机器人基坐标系标定方法
Calibration method of robot base frame by quaternion form
北京航空航天大学学报, 2015, 41(3): 411-417
Journal of Beijing University of Aeronautics and Astronsutics, 2015, 41(3): 411-417.
http://dx.doi.org/10.13700/j.bh.1001-5965.2014.0239

文章历史

收稿日期: 2014-04-30
录用日期: 2014-06-12
网络出版时间：2014-12-09

相关文章

工作空间