Download PDF  
文章快速检索  
  高级检索
引用本文
李成, 郭婷婷, 肖俊, 樊尚春, 靳伟. 基于石墨烯膜的光纤Fabry-Perot腔干涉特性分析[J]. 北京航空航天大学学报, 2015, 41(4): 574-579
LI Cheng, GUO Tingting, XIAO Jun, FAN Shangchun, JIN Wei. Interference characteristics analysis of optical fiber Fabry-Perot cavity with graphene diaphragm[J]. Journal of Beijing University of Aeronautics and Astronsutics, 2015, 41(4): 574-579.
基于石墨烯膜的光纤Fabry-Perot腔干涉特性分析
李成1,2, 郭婷婷1,2, 肖俊1,2, 樊尚春1,2, 靳伟3    
1. 北京航空航天大学 “新型惯性仪表与导航系统技术”国防重点学科实验室, 北京 100191;
2. 北京航空航天大学 仪器科学与光电工程学院, 北京 100191;
3. 香港理工大学 电机工程学系, 九龙
收稿日期:2014-5-19; 录用日期: 2014-06-12; 网络出版日期: 2014-07-08
基金项目：国家自然科学基金资助项目(61273060,61121003); 长江学者和创新团队发展计划资助项目(IRT1203); 中央高校基本科研业务费专项资金资助项目(YWF-13-B03-C11,YWF-14-YQGD-004); 北航研究生创新实践基金资助项目(YCSJ-01-2014-11); 中国空间技术研究院CAST创新基金资助项目.
通讯作者: 李成(1977—),男,天津人,副教授,licheng@buaa.edu.cn,主要研究方向为先进传感与智能仪器.
摘要：针对以新型材料石墨烯为膜片的光纤法珀压力传感器,应用圆薄膜大挠度弹性理论,利用有限元法分析了均布载荷下石墨烯膜的挠度形变;并基于Fabry-Perot干涉仪原理,建立了光纤Fabry-Perot腔压力传感的数学模型.根据石墨烯膜折射率特性,分析了层数、入射光角度等参数对石墨烯膜反射率的影响,获取了腔长损耗以及薄膜挠度形变导致腔长变化而引起的干涉光谱变化规律.仿真结果表明,增加薄膜层数可提高反射率、改善干涉性能;但随着载荷增加,其对挠度形变的影响表现为反向递减效应.8层石墨烯薄膜可获得0.715%的反射率,且当腔长为40μm时,直径25μm薄膜的理论压力灵敏度约为10nm/kPa.这为基于多层石墨烯的膜片式光纤压力传感器的设计提供了理论依据.
关键词： 光纤Fabry-Perot腔     石墨烯膜     大挠度     干涉特性     压力传感器    
Interference characteristics analysis of optical fiber Fabry-Perot cavity with graphene diaphragm
LI Cheng1,2 , GUO Tingting1,2, XIAO Jun1,2, FAN Shangchun1,2, JIN Wei3     
1. Novel Inertial Instrument & Navigation System Technology Key Laboratory of Fundamental Science for National Defense, Beijing University of Aeronautics and Astronautics, Beijing 100191, China;
2. School of Instrumentation Science and Opto-electronics Engineering, Beijing University of Aeronautics and Astronautics, Beijing 100191, China;
3. Department of Electrical Engineering, The Hong Kong Polytechnic University, Jiulong, China
Abstract:With regard to the design of optical fiber Fabry-Perot cavity using graphene as sensitive diaphragm, the deflection change under uniformly distributed loads in graphene film was analyzed by finite element method based on the large deflection elastic theory of circular film. The pressure-sensing mathematical model of optical fiber Fabry-Perot cavity with graphene diaphragm was established based on the working principle of Fabry-Perot interferometer. The effects of graphene film layer and incident light angle on the film reflectivity were obtained according to the refractive index characteristics of the film. Then the interference spectra change, caused by both the cavity length losses and the film deflection deformations under the pressure loads, were analyzed. The simulation results show that adding the film layer can increase the film reflectivity and further improve the optical interference performance; however, a decreasing effect on the deflection deformation is caused by the film layer with the increase of pressure load. Thus, an 8 layer graphene film can achieve a reflectivity of 0.715% and an approximate theoretical sensitivity of 10 nm/kPa for a 40 μm Fabry-Perot cavity length with a membrane diameter of 25 μm. It provides a theoretical basis for the design and fabrication of high-sensitivity fiber-tip pressure sensor with multiple-layer graphene diaphragm.
Key words: optical fiber Fabry-Perot cavity     graphene diaphragm     large deflection     interference characteristics     pressure sensor    

2004年,英国曼彻斯特大学Novoselov和Geim等用微机械剥离方法首次获得了单层石墨烯薄膜[1].作为自然界中已知的最薄的膜材料,单层石墨烯的厚度为0.335 nm,其断裂强度为42 N/m,是不锈钢的100倍,弹性模量接近1 TPa,弹性延展率可达20%,其不透明度为(2.3±0.1)%,反射率小于0.1%;但不透明度随薄膜层数的增加而变大,梯度约为2.3%[2, 3, 4].随着石墨烯制备及转移方法的不断发展[5, 6],石墨烯薄膜优良的机械特性和光学特性受到了研究者的广泛关注.2008年,美国康奈尔大学Bunch等对石墨烯薄膜的不透气性进行了理论与实验研究[7],这为石墨烯材料用于压力传感器的敏感薄膜提供了可能.2012年,瑞典KTH皇家理工学院Smith等提出了悬浮石墨烯压力传感器的结构与制造工艺,并运用喇曼光谱仪对石墨烯的变形进行了分析,在13 978 Pa压力下单层石墨烯的最大变形可达280 nm[8].但所用SiO2与SiC基底的性质逊于石墨烯的内在性质,对传感器的结构与功能产生一定局限性.2013年,韩国世明大学Kwon等利用顶板结构借助压力传递效应,提出了一种改进的悬浮石墨烯压力传感器[9],其在低压范围内具有较好的线性度,但在高压范围内线性度较差,且结构尺寸相对于一般悬浮石墨烯压力传感器较大.2012年,香港理工大学Ma等以直径125 μm的石墨烯膜为感压元件制作了光纤F-P腔压力传感器,其灵敏度为1 100 nm/kPa[10, 11].

以上理论与实验研究表明,作为压力敏感薄膜,石墨烯具有比硅材料更高的灵敏度和抗过载能力,在高灵敏度动态压力测量方面具有较高的应用前景,但这方面的研究才刚起步.本文基于圆薄膜大挠度理论,借助有限元力学分析,对石墨烯膜的压力-挠度进行了建模仿真,并针对挠度形变的高灵敏度检测,分析了石墨烯膜对光纤F-P腔压力传感特性的影响.

1 F-P腔压力敏感模型

图 1为基于石墨烯膜的光纤F-P腔结构示意图.当光纤内入射光垂直入射到光纤端面时,一部分光被光纤端面反射,剩余光透射进入F-P腔体,在F-P腔体内产生多光束干涉,从而形成光纤F-P腔传感器.作为该传感器敏感单元的石墨烯膜感受外界均布载荷q,由于单层石墨烯膜厚约0.335 nm,在均布压强下其挠度形变远大于膜厚,挠度特性表现为非线性.

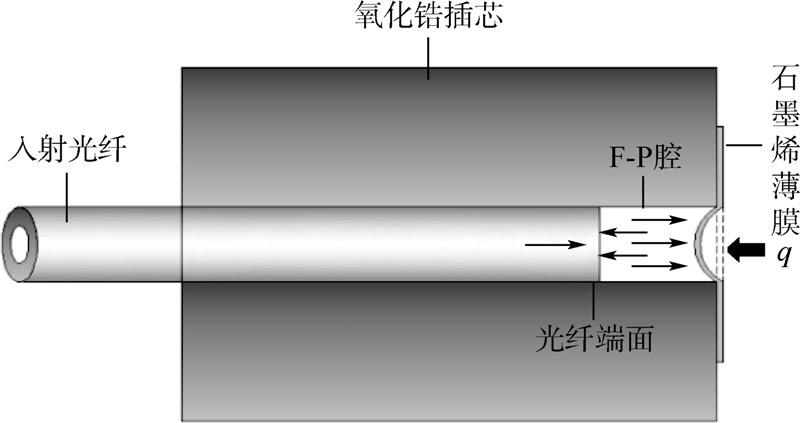图 1 F-P腔结构示意图Fig. 1 Schematic diagram of F-P cavity
图选项

考虑到薄膜应力使膜片弯曲,而弯曲曲率半径与薄膜应力、膜片特性、厚度密切相关,1959年,Beams通过鼓泡实验获取沉积在基体上的薄膜力学性能,提出了考虑预应力σ0条件下的球壳模型,即当圆形薄膜受均布面载荷时薄膜发生均匀对称的膨胀,其挠度满足的公式为[12]

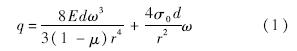
式中,E为弹性模量;d为薄膜厚度;μ为泊松比;r为圆薄膜半径;ω为薄膜中心挠度.为此,利用ANSYS有限元法,构建了压力作用下的石墨烯膜中心挠度的仿真模型.

为此,考虑光纤F-P腔压力传感器的微小型设计,结合文献[10]的石墨烯膜参数,以半径为12.5 μm的单层石墨烯圆薄膜为分析对象.该膜片边界条件为周边固支,材料参数选用Lee等通过原子力显微镜实测的结果[3],即E，σ0，d，μ分别为1 TPa，1.2 GPa，0.335 nm，0.17.在0~50 kPa范围内分别对预应力作用下的1,3,5,8层石墨烯圆膜片施加均布载荷,则石墨烯膜均布载荷下中心挠度特性仿真结果如图 2所示.可知,Beams模型的解析解与ANSYS仿真解之间的平均相对误差为0.49%,从而表明式(1)可用于分析均布载荷下石墨烯膜的中心挠度特性.这样,当探头受到外界均布载荷q时,薄膜中心挠度ω使腔长由初始值L0缩短至L,即

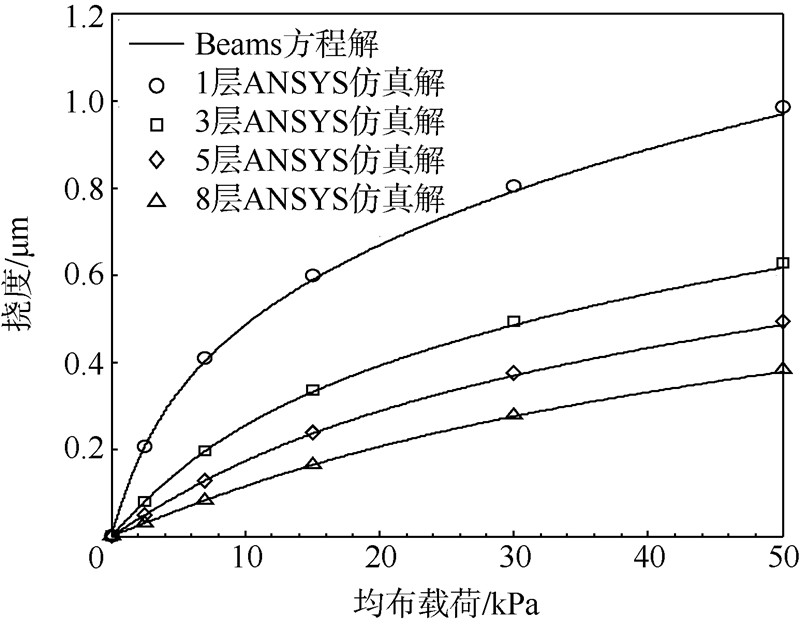图 2 石墨烯膜均布载荷下中心挠度特性仿真Fig. 2 Deflection characteristic simulation under uniform load of single-layer graphene film
图选项
则F-P腔输出的多光束干涉光强Ir为[13]
式中,Ii为入射光强;R1，R2分别为F-P腔内光纤端面和石墨烯薄膜的反射率,R1取实测值0.02,R2由薄膜特性矩阵确定;δ为无半波损失时的相邻光束的相位差;ξ为F-P腔长耦合系数.特别地,当光垂直入射,且腔体内介质为空气时,δ可表示为
式中,λ为入射光波长.由式(3)可知,干涉光谱为近似等周期的余弦函数,当δ=(2m+1)π,m=0,1,…时Ir取得峰值.取对应干涉光谱中级次为m和m+k的峰值,则

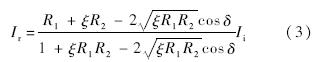
因此,由外界均布载荷q、薄膜中心挠度ω、F-P腔腔长L等构成的压力传感模型可由式(1)、式(2)和式(6)联立确定.

2 特性仿真 2.1 石墨烯薄膜厚度对反射率的影响

由于入射光射入石墨烯薄膜存在一定的角度,分别考虑薄膜对p-偏振光和s-偏振光的反射率Rp，Rs.根据薄膜光学理论,可得薄膜及其外侧空气的特性矩阵为[14]

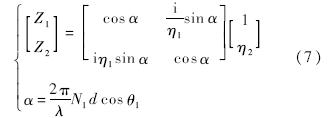
式中,i为虚数单位;η1为石墨烯薄膜的有效导纳;η2为空气的有效导纳;薄膜厚度d=薄膜层数×单层膜厚;N1为石墨烯薄膜复折射率.对于p-偏振光,η1=N1/cos θ1,η2=1/cos θ2(空气折射率≈1),而对于s-偏振光,η1=N1cos θ1,η2=cos θ2,其中,θ1为空气界面与薄膜的折射角,θ2为薄膜与空气界面的出射角.

且石墨烯膜的反射系数可表示为[14]

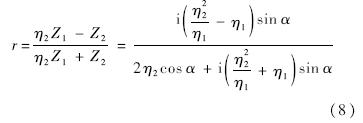
将p-偏振光和s-偏振光对应的不同有效导纳代入式(8),可求取相应的反射系数rp,rs及其共轭复数rp*,rs*,则石墨烯膜反射率R2由式(9)确定:

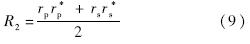
为简化分析,假设入射光垂直入射到薄膜,则对于p-偏振光和s-偏振光,对应介质的有效导纳相等,且有η1=N1,η2=1,α=2π(N1·d)/λ,rp=rs=r,则式(9)可简化为

式中

由式(10)可知,石墨烯薄膜的反射率R2与其复折射率N1有关.取N1=n1－jk1,其中j为虚数单位,n1为折射率,k1为消光系数,参数n1，k1随入射光波长的变化参考基于椭圆偏振法的石墨烯膜折射率测量实验确定[15],则不同入射光波长下薄膜层数对反射率的影响如图 3所示.

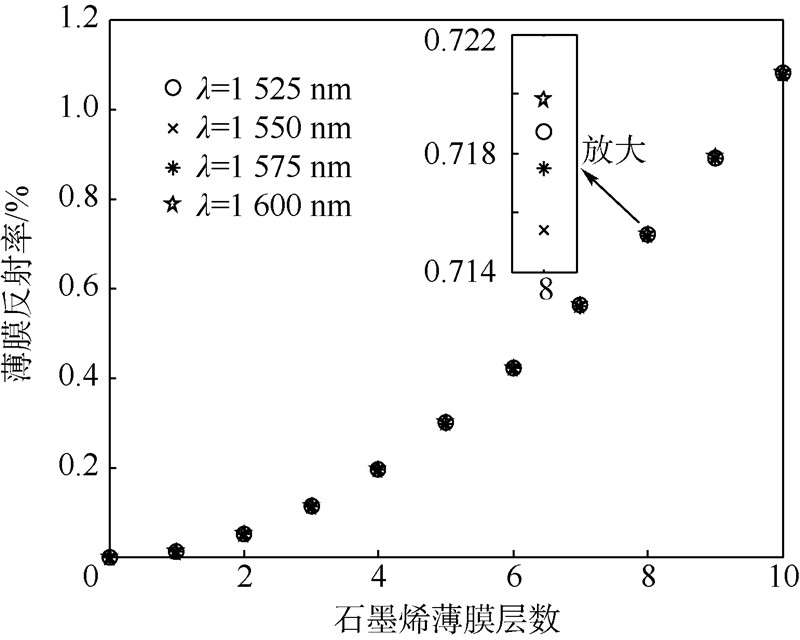图 3 不同入射光波长下薄膜层数对反射率的影响Fig. 3 Effects of graphene layer on film reflectivity in different wavelengths of incident light
图选项

当石墨烯膜为9层以下时,其反射率低于1%.这表明在F-P腔内石墨烯膜的反射光强度很弱,入射光强几乎被透射或损耗.但随膜厚增加,其反射率随之单调变大.而且,以8层石墨烯膜为例,当波长为1 600 nm和1 550 nm时薄膜反射率分别为0.718 9%和0.715 4%,两者相差仅为0.003 5%.这样,当自由光谱范围FSR较小时可忽略入射光波长对反射率的影响.

考虑到石墨烯膜利用范德瓦尔斯力实现石墨烯薄膜与氧化锆陶瓷光纤插芯端面的吸附以制作F-P腔.因此,悬浮于插芯中孔处的石墨烯膜的微小不平整性将会使入射角度发生微小改变,则入射光角度(θ0)对石墨烯膜反射率的影响如图 4所示.

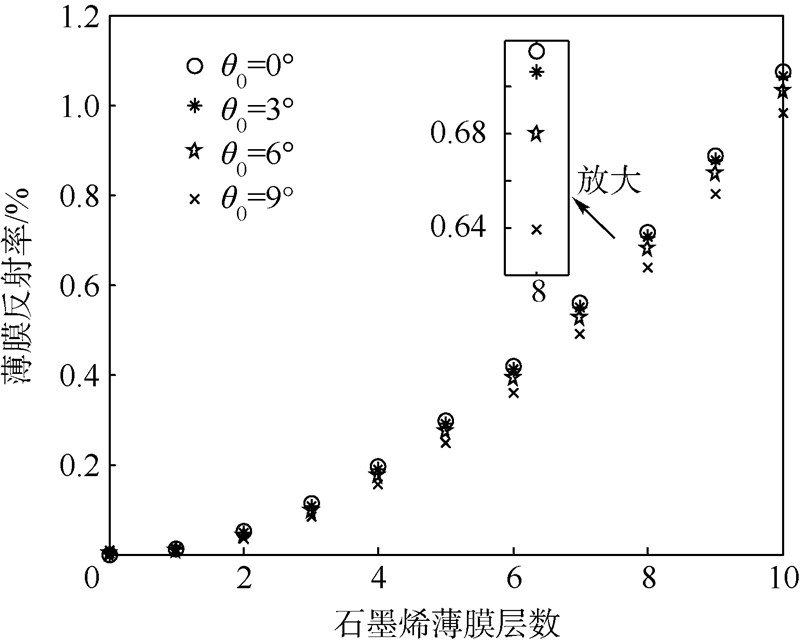图 4 入射光角度对石墨烯膜反射率的影响Fig. 4 Effects of incident light angle on graphene film reflectivity
图选项

仿真结果表明,随着薄膜变厚,入射光角度对薄膜反射率的影响逐渐显现,但并不明显.以8层石墨烯膜为例,当入射角度(θ0)为0°,3°,6°,9°时,薄膜反射率依次为0.715 4%,0.706 3%,0.679 8%,0.638 9%.这表明在F-P腔内石墨烯薄膜反射率随入射光角度的增加会发生小幅减小,但减小的趋势有限.因此,对于在内径25 μm的光纤凹槽以及125 μm陶瓷插芯内形成的微小F-P腔,因薄膜吸附变形而引起的入射光小角度变化对反射率的影响可忽略.

2.2 腔长损耗影响

膜片式F-P腔光纤传感器受腔长影响,其干涉光强度损耗可由耦合系数ξ确定[16]:

式中
其中,lR为瑞利距离;w0为光场在光纤中传播的模场半径;w(l)为光在F-P腔中传播的模场半径;l为光在F-P腔内传播的距离;N0为F-P腔中的介质折射率.F-P腔为空气隙且光纤为SMF-28单模光纤,则N0=1,w0=4.9 μm.即耦合系数是入射光波长λ和腔长L(L=l/2)的函数,其值越大,光强损耗越小.

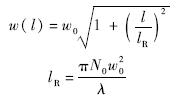
图 5为入射光波长为1 500,1 550,1 600 nm时F-P腔干涉光耦合曲线.由此可知,对于固定腔长,波长对F-P腔光强损耗的影响较弱.以L=40 μm为例,波长由1 500 nm变化至1 600 nm所引起的耦合系数仅差0.038 1.但腔长变化对光强损耗的影响更为明显.以λ=1 550 nm为例,当腔长大于50 μm时,耦合系数小于0.6,从而使干涉信号光强大幅损耗.为此,需选用小F-P腔以提高干涉光强信号的检测性能.

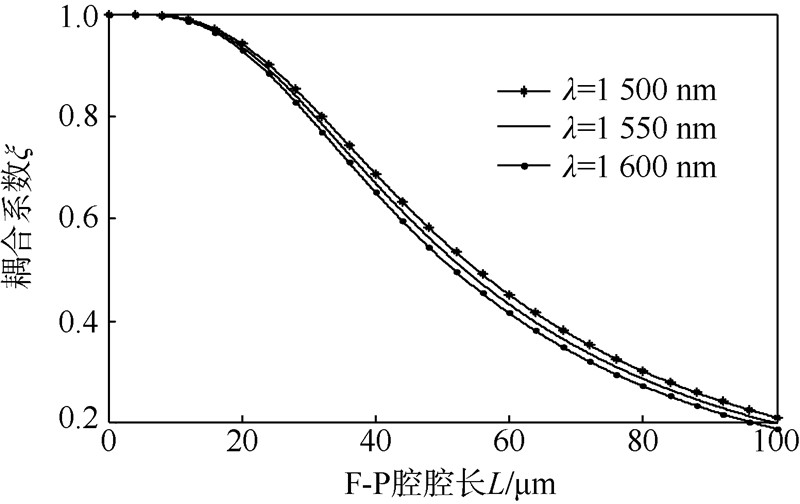图 5 F-P腔干涉光耦合曲线Fig. 5 Interference light coupling curves of Fabry-Perot cavity in different lengths
图选项

取无量纲相对光强为10lg(Ir/Ii),由式(3)可获取干涉光谱曲线,则当入射波长为1 550 nm时,1,3,5,8层石墨烯薄膜(反射率分别为0.013%,0.112%,0.297%,0.715%)的干涉光谱如图 6所示.图中n表示层数;Y,N表示有无考虑腔长损耗.仿真结果表明,波长变化引起的腔长损耗主要影响干涉光谱的相对光强峰值,不改变曲线形状,且这种影响与薄膜厚度密切相关.通过增加膜厚可使薄膜反射率单调正向变化,改善干涉光谱的对比度,提高检测信号的干涉效果.

图 6 不同层厚石墨烯薄膜的干涉光谱Fig. 6 Interference spectra of graphene film with different thicknesses
图选项
2.3 均布载荷对F-P腔干涉的影响

针对均布载荷对石墨烯膜光纤F-P腔信号检测的影响,结合获取的石墨烯膜机械力学特性(第1节)和光学反射特性(2.1~2.2节),以单层和8层的周边固支圆薄膜为例,取F-P初始腔长为40 μm,图 7为均布载荷下单层及8层石墨烯膜的F-P腔干涉光谱.由此可知,对周边固支的直径为25 μm的圆薄膜施加均布载荷,在1 520~1 590 nm范围内光纤信号表现为干涉光谱特征,且随着载荷以10 kPa为间隔由0递增至50 kPa,其腔长变化量ΔL及干涉光谱峰值对应的波长偏移量Δλ如表 1所示.

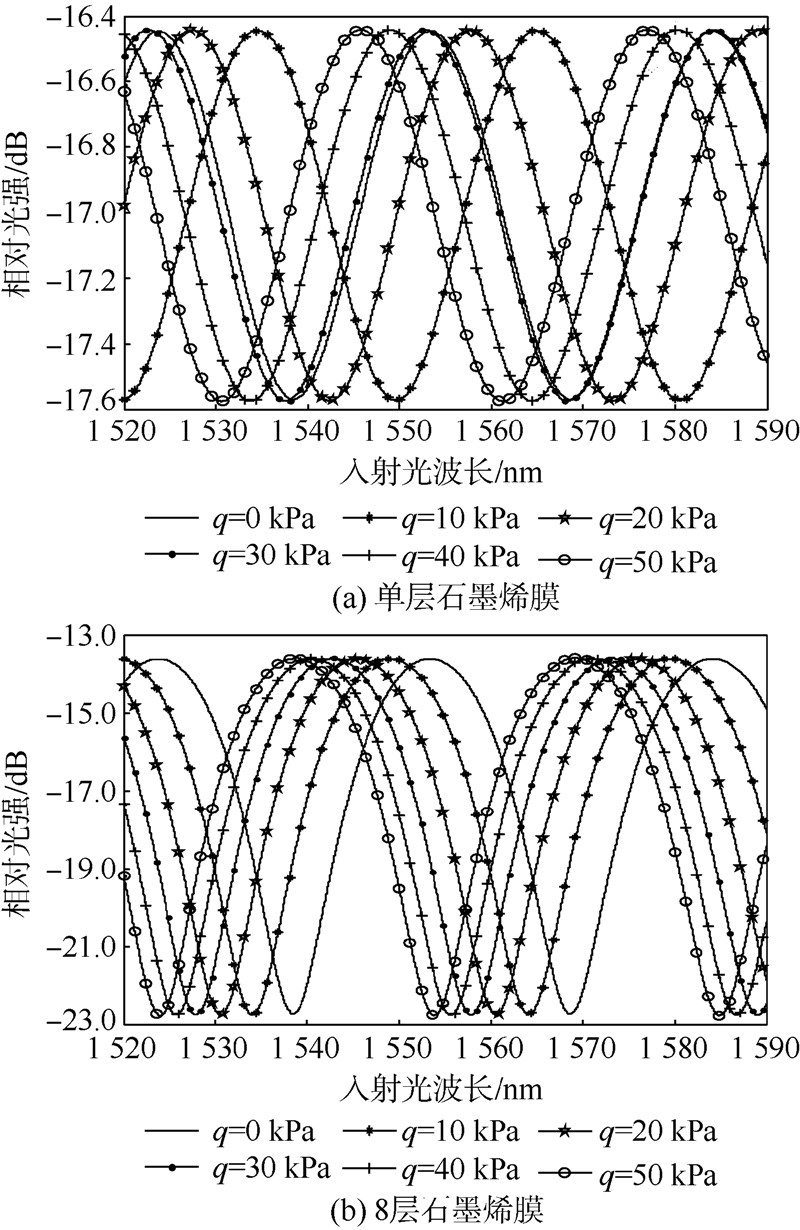图 7 均布载荷下单层及8层石墨烯膜的 F-P腔干涉光谱Fig. 7 Fabry-Perot interference spectra for single-layer and 8-layer graphene film under uniformly distributed loads
图选项
表 1 不同均布载荷下波长与腔长的变化 Table 1 Change of incident light wavelength and F-P cavity under uniformly distributed loads
载荷/kPa单层8层
ΔL/nmΔλ/nmΔL/nmΔλ/nm
1048519.211154.47
2066826.462068.00
3079131.3327510.68
4088835.1733112.85
5096838.3437714.64

表选项

仿真结果表明,一方面,增加薄膜厚度将降低挠度变形及其干涉光谱峰值处波长的偏移量,但另一方面,随着薄膜层数的增加,石墨烯压力-位移特性曲线的曲率变小,使非线性得到相应改善,不过对压力的敏感程度则相对降低.特别地,对于所用40 μm腔长,单层石墨烯膜F-P腔的干涉对比度为0.128,其明显低于8层石墨烯膜的0.782.如将图 7中干涉信号光谱转化至对数域,则相对光强的峰-峰值分别约为1.12 dB和9.13 dB.考虑到光谱仪AQ6370C的0.1 dB/Div功率精度,双峰法可分辨出8层石墨烯膜的F-P干涉光谱,则由直径25 μm的石墨烯膜挠度特性,其理论压力灵敏度约为10 nm/kPa.而且,通过调整薄膜结构尺寸及薄膜与F-P腔基体的吸附性能可有效改善传感器灵敏度与干涉光谱信号提取.

3 结 论

1) 针对超薄石墨烯薄膜在高灵敏度压力传感中的潜在应用,根据薄膜大挠度理论,应用Beams球壳模型和ANSYS有限元方法,对石墨烯膜大挠度力学特性进行了数值解析与有限元分析,两者间0.49%的平均相对误差验证了Beams球壳模型用于石墨烯薄膜大挠度形变特性分析的有效性.

2) 考虑光纤F-P腔的多光束干涉效应,仿真求取了膜厚、入射光的波长、角度等参数对薄膜反射率以及干涉光谱的影响规律.结果表明,膜厚对膜片中心挠度形变及其干涉光谱强度起主要影响,但2种影响表现为相反的作用效果.

3) 根据石墨烯膜的干涉对比度仿真分析,直径25 μm的8层石墨烯圆薄膜具有0.715%的反射率,当F-P腔长设计为40 μm时其可实现约为10 nm/kPa的理论压力灵敏度.

参考文献
[1] Novoselov K S, Geim A K,Morozov S V,et al.Electric field effect in atomically thin carbon films[J].Science,2004,306(5696):666-669.
Click to display the text
[2] Liang X, Sperling B A,Calizo I,et al.Toward clean and crackless transfer of graphene[J].ACS Nano,2011,5(11):9144-9153.
Click to display the text
[3] Lee C, Wei X D,Kysar J W,et al.Measurement of the elastic properties and intrinsic strength of monolayer graphene[J].Science,2008,321(5887):385-388.
Click to display the text
[4] Nair R R, Blake P,Grigorenko A N,et al.Fine structure constant defines visual transparency of graphene[J].Science,2008,320(5881):1308.
Click to display the text
[5] 袁小亚. 石墨烯的制备研究进展[J].无机材料学报,2011,26(6):561-570. Yuan X Y.Progress in preparation of graphene[J].Journal of Inorganic Materials,2011,26(6):561-570(in Chinese).
Cited By in Cnki (51)
[6] Martins L G P, Song Y,Zeng T,et al.Direct transfer of graphene onto flexible substrates[J].Proceedings of the National Academy of Sciences,2013,110(44): 17762-17767.
Click to display the text
[7] Bunch J S, Verbridge S S,Alden J S,et al.Impermeable atomic membranes from graphene sheets[J].Nano Letters,2008,8(8):2458-2462.
Click to display the text
[8] Smith A D, Vazirs S,Delin A,et al.Strain engineering in suspended graphene devices for pressure sensor application[C]//Proceedings of the 13th International Conference on Ultimate Integration on Silicon.Grenoble,France:IEEE,2012:21-24.
Click to display the text
[9] Kwon O K, Lee J H,Kim K S,et al.Developing ultrasensitive pressure sensor based on graphene nanoribbon:molecular dynamics simulation[J].Physica E:Low-Dimensional Systems and Nanostructures,2013,47:6-11.
Click to display the text
[10] Ma J,Jin W, Ho H L,et al.High-sensitivity fiber-tip pressure sensor with graphene diaphragm[J]. Optics Letters,2012,37(13): 2493-2495.
Click to display the text
[11] Ma J, Xuan H F,Ho H L,et al.Fiber-optic Fabry-Perot acoustic sensor with multilayer graphene diaphragm[J].IEEE Photonics Technology Letters,2013,25(10):932-935.
Click to display the text
[12] Beams J W. The structure and properties of thin film[M].New York:John Wiley and Sons,1959:183-190.
[13] Zhou X, Yu Q.Wide-range displacement sensor based on fiber-optic Fabry-Perot interferometer for subnanometer measurement[J].IEEE Sensors Journal,2011,11(7):1602-1606.
Click to display the text
[14] 唐晋发,顾培夫. 薄膜光学与技术[M].北京:机械工业出版社,1989:5-24. Tang J F,Gu P F.Thin film optics and technology[M].Beijing:China Machine Press,1989:5-24(in Chinese).
[15] Nelson F J, Kamineni V K,Zhang T,et al.Optical properties of large-area polycrystalline chemical vapor deposited graphene by spectroscopic ellipsometry[J].Applied Physics Letters,2010,97(25):253110.
Click to display the text
[16] Ma C, Dong B,Gong J,et al.Decoding the spectra of low-finesse extrinsic optical fiber Fabry-Perot interferometers[J].Optics Express,2011,19(24):23727-23742.
Click to display the text
http://dx.doi.org/10.13700/j.bh.1001-5965.2014.0279
北京航空航天大学主办。
0

文章信息

李成, 郭婷婷, 肖俊, 樊尚春, 靳伟
LI Cheng, GUO Tingting, XIAO Jun, FAN Shangchun, JIN Wei
基于石墨烯膜的光纤Fabry-Perot腔干涉特性分析
Interference characteristics analysis of optical fiber Fabry-Perot cavity with graphene diaphragm
北京航空航天大学学报, 2015, 41(4): 574-579
Journal of Beijing University of Aeronautics and Astronsutics, 2015, 41(4): 574-579.
http://dx.doi.org/10.13700/j.bh.1001-5965.2014.0279

文章历史

收稿日期：2014-5-19
录用日期: 2014-06-12
网络出版日期: 2014-07-08

相关文章

工作空间