近年来,平流层浮空器(SLV,Stratosphere Lighter-than-air Vehicle)受到很大的重视,世界各主要国家均开展了相关的研究与试验.平流层浮空器具有定点驻留、超长航时、视野范围广、生存能力强的特点,具有重要的民用和军用价值[1].平流层浮空器主要有“艇型”和“球形囊体型”两大类.“艇型”平流层浮空器具有气动阻力小的优点,但受限于目前的超压蒙皮材料技术,未来一段时间内“艇型”平流层浮空器在解决平流层的昼夜温差问题还有一定难度[2].“球形囊体型”平流层浮空器是近期内在平流层长时驻空一种有效的途径.
“球形囊体型”相比“艇型”平流层浮空器存在阻力大、气动力波动幅度大等不足.因此,研究“球形囊体型”平流层浮空器的气动特性并且通过合理设计减阻对其总体设计具有重要意义.对于球体绕流问题,当雷诺数增加到某一值,球体表面边界层由层流变成湍流,推迟了边界层分离,压差阻力减少,阻力系数急剧下降,这种现象称为“失阻”,对应的雷诺数称为临界雷诺数.由于“球形囊体型”平流层浮空器尺度大,对应的雷诺数就会很大,气动模型简化为超临界雷诺数范围的多球体绕流问题.在超临界雷诺数范围时,球体尾流中的流动为湍流状态,流场具有复杂结构,呈明显的非定常性.
国外,Sakamoto和Haniu系统地总结了前人的研究成果,并且通过流场显示试验和热线试验,测量了球体在很广的雷诺数范围内的斯特劳哈尔数St[3].Constantinescu和Squires在总结前人研究成果的基础上,给出了球体的阻力系数随雷诺数的变化情况,并对临界雷诺数时球体的绕流进行了分析,绘制了典型条件下球体的绕流图画[4].Rodriguez等通过直接数值模拟方法研究了雷诺数为3700和10000时的球体绕流问题.研究发现,尾流受控于3个不稳定因素:大规模涡流脱落频率,小规模Kelvin-Helmholtz不稳定剪切层频率以及再流通区域变化频率[5].Moradian等通过试验研究了雷诺数为2.2×104~8×104时,雷诺数、湍流强度和整体尺度对球体阻力系数的影响[6].Hassanzadeh等通过大涡模拟(LES,Large Eddy Simulation)方法,研究了单球体和不同间距的并列双球体的绕流问题[7, 8].Pinar等则通过试验研究了雷诺数为5000时并列双球体的流场结构[9].国内,邹建峰等[10]采用自编的分块算法程序模拟了雷诺数在20~1000之间的球体绕流场.任安禄等[11]采用三维黏性不可压缩流场分块耦合计算方法研究球体绕流问题.邹建峰和任安禄[12]对虚拟边界法加以改善并推广到三维多连通区域的数值模拟中去,研究了低雷诺数下串列双圆球的流场转捩现象.
国内外学者对球体绕流问题的研究主要集中在临界雷诺数以下,对于大尺度低速不可压超临界雷诺数范围的球体绕流问题研究几乎空白.
本文将“球形囊体型”平流层浮空器的气动模型简化为超临界雷诺数范围的串列双球体绕流问题,运用大涡模拟研究了两球体的间距对气动特性的影响.
1 数值模拟方法 1.1 控制方程
三维牛顿不可压流体控制方程为
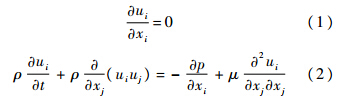
在大涡模拟中,通过滤波函数将流动变量划分为大尺度量和小尺度量两部分:
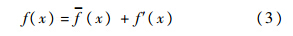
大尺度量用如下形式来表示:
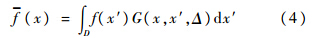
滤波函数G(x,x′)可以表示为
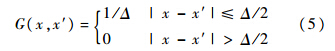
对控制方程进行空间滤波,得到大涡模拟的基本方程为
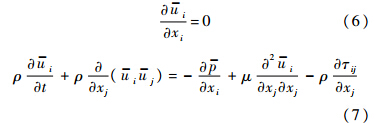
本文采用Smagorinsky-Lilly亚格子模型[13, 14],亚格子应力定义为
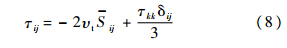
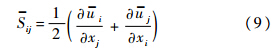
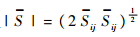 ;δij为Kronecker记号;Cs为Smagorinsky常数.
;δij为Kronecker记号;Cs为Smagorinsky常数.1.2 计算模型
计算流域是横截面为正方形的长方体,囊体按球体处理,球体的直径为D,坐标原点在上游球体球心,上下游球体球心的间距为G(G为0时则是单球体的情况),x轴正方向指向压力出口,y轴正方向指向上方,z轴正方向由右手准则确定,速度入口平面距坐标原点为4D,压力出口平面距坐标原点为10D,计算域横截面为边长为8D的正方形,来流速度为V0,如图 1和图 2所示.
 |
| 图 1 流场侧视图 Fig. 1 Side view of flow field |
 |
| 图 2 流场正视图 Fig. 2 Front view of flow field |
计算流域网格采用O形结构网格,附面层第一层网格的y+值为0.5,空间最小网格步长位于近壁面,约为0.6×10-5D,球体表面网格与近壁面网格如图 3和图 4所示.
 |
| 图 3 球体表面网格图 Fig. 3 Surface grid of sphere |
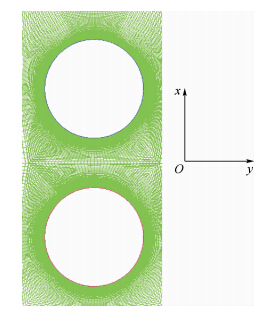 |
| 图 4 球体近壁面网格图 Fig. 4 Near wall grid of sphere |
边界条件设为速度入口、压力出口和壁面.由于已知来流速度,将入口边界定义为速度入口条件;球体表面定义为无滑移壁面边界条件;出口边界定义为压力出口边界条件.
1.4 计算方法
数值模拟采用Fluent软件平台,采用有限体积法对控制方程进行离散化,大涡模拟控制方程采用有限二阶隐式法推进,对流项的离散格式采用有限中心差分格式.
2 计算结果 2.1 方法验证:单球体(G=0)
为了检验计算方法的准确性,先计算单球体在超临界雷诺数范围时(Re=1.41×106,1.88×106)的非稳态情况.
阻力系数定义为
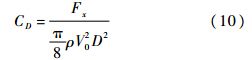
y和z方向侧力系数定义为
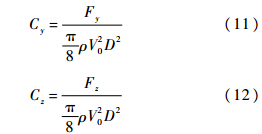
横向合力系数定义为
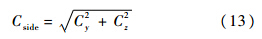
阻力系数随时间变化如图 5和图 6所示.Re=1.41×106时,阻力系数在0.1278~0.1442间波动,时均值为0.1367;Re=1.88×106时,阻力系数在0.1315~0.1602间波动,时均值为0.1428.Achenbach通过试验测量了球体在Re=5×104~6×106的阻力系数[15],从Achenbach给出的试验数据插值出Re=1.41×106,1.88×106时的阻力系数,试验值分别为0.135和0.140.计算结果对比如表 1所示.
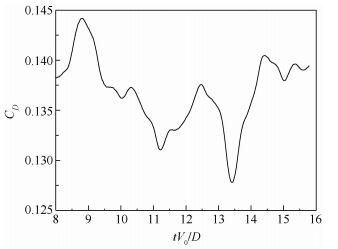 |
| 图 5 Re=1.41×106时,阻力系数随时间变化图 Fig. 5 Time history of drag coefficient at Re=1.41×106 |
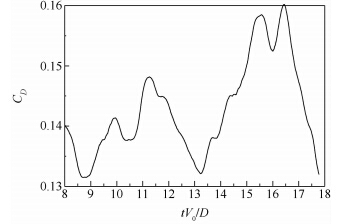 |
| 图 6 Re=1.88×106时,阻力系数随时间变化图 Fig. 6 Time history of drag coefficient at Re=1.88×106 |
| Re | CD计算 | CD试验 | 误差/% |
| 1.41×106 | 0.1367 | 0.135 | 1.26 |
| 1.88×106 | 0.1428 | 0.140 | 2 |
由表 1可以看出本文的计算结果与Achenbach的试验结果吻合良好,验证了本文方法在分析超临界雷诺数球体绕流问题时的准确性.
2.2 双球体
通过计算超临界雷诺数Re=1.41×106时,不同间距的非稳态情况.上下游球体球心的间距为D时,阻力系数随时间变化如图 7所示.图中:CD-1表示上游球体的阻力系数;CD-2表示下游球体的阻力系数;CD-all表示两球合阻力系数.上游球体的阻力系数时均值为0.0093,下游球体的阻力系数时均值为0.2090,两球合阻力系数时均值为0.2183.
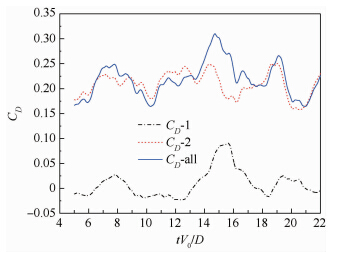 |
| 图 7 G=D时,阻力系数随时间变化图 Fig. 7 Time histories of drag coefficient when G=D |
上下游球体球心的间距为1.5D时,阻力系数随时间变化如图 8所示.上游球体的阻力系数时均值为0.0925,下游球体的阻力系数时均值为0.3142,两球合阻力系数时均值为0.4067.
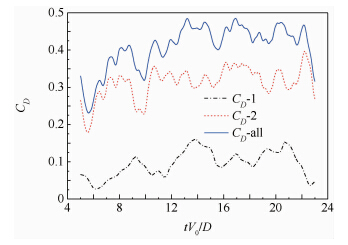 |
| 图 8 G=1.5D时,阻力系数随时间变化图 Fig. 8 Time histories of drag coefficient when G=1.5D |
上下游球体球心的间距为2D时,阻力系数随时间变化如图 9所示.上游球体的阻力系数时均值为0.1101,下游球体的阻力系数时均值为0.1874,两球合阻力系数时均值为0.2975.
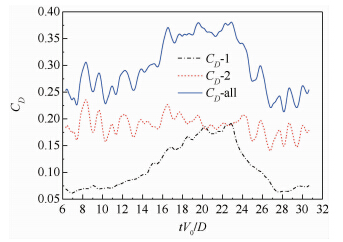 |
| 图 9 G=2D时,阻力系数随时间变化图 Fig. 9 Time histories of drag coefficient when G=2D |
上下游球体球心的间距为3D时,阻力系数随时间变化如图 10所示.上游球体的阻力系数时均值为0.1934,下游球体的阻力系数时均值为0.1087,两球合阻力系数时均值为0.3021.
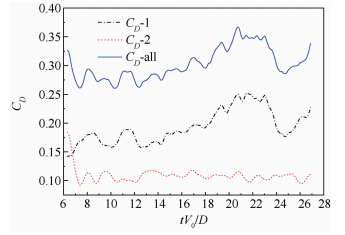 |
| 图 10 G=3D时,阻力系数随时间变化图 Fig. 10 Time histories of drag coefficient when G=3D |
图 11给出了阻力系数随间距的变化情况.随着上下游球体距离G的增加,上游球体的阻力系数逐渐增大,下游球体的阻力系数先增大后减小,在G=1.5D时有最大值.两球合阻力系数也先增大后减小,G=D时为最小值,G=1.5D时为最大值,G=2D和G=3D时基本相同.
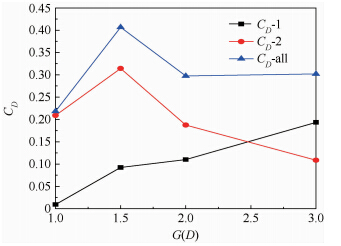 |
| 图 11 阻力系数随间距变化图 Fig. 11 Drag coefficient varies with distance |
进一步分析阻力振动的频谱特性,运用快速傅里叶变换,将时域上的数据变化到频域上,得到了阻力系数和横向合力系数在频域上的幅度特征.上下游球体阻力系数频谱特征如图 12所示.当G=D时,上游球体的占优频率为0.118;下游球体的占优频率为0.176,但下游球体还存在二、三、四次频,分别为0.412,0.059,0.294,这3个次频的幅度值相差不大,与占优的主频形成竞争的态势.当G=1.5D时,上游球体的占优频率为0.050,还存在二、三次频,分别为0.151,0.252;下游球体的占优频率与上游球体相同,还存在与主频幅度值接近的二次频,频率为0.504,三、四次频的频率分别为0.202,0.303.当G=2D时,上下游球体存在相同的占优频率0.041,下游球体还存在较多竞争的次频,频率范围为0.123~0.739.当G=3D时,上游球体的占优频率为0.049;下游球体的占优频率为0.292,还存在较多竞争的次频,频率范围为0.097~0.632.
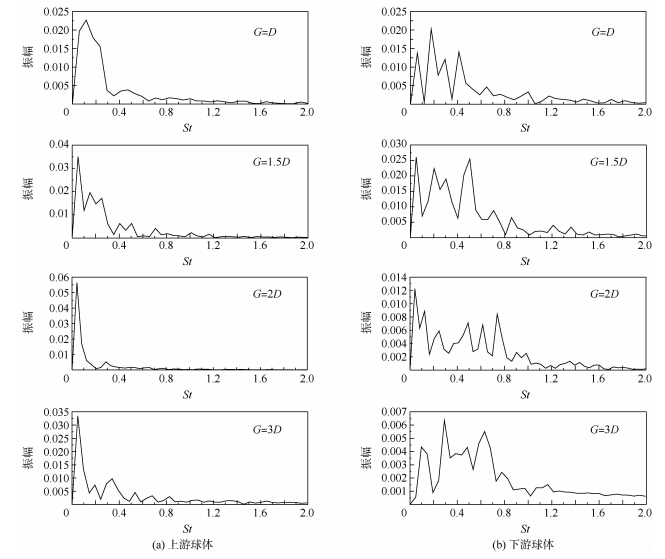 |
| 图 12 上下游球体阻力系数频谱特征图 Fig. 12 Frequency spectrum of upstream and downstream spheres’drag coefficients |
图 13显示了不同间距流向无量纲时均速度(u/V0)的分布.从图中可以看出,在球体背风面均有负速度分布.G=D时,由于两球接触而在球间形成凹槽,在上游球体的侧后方最小的流向速度达到了-0.50,是4种间距中最小的,说明该位置有很强的流向回流,但是该间距对应的流向回流区域却是4种情况中最小的,球体所受的压差阻力最小,而球体的阻力主要与压差阻力相关,因 此上游球体的阻力系数在4种情况中最小;下游球体的流向回流速度分布长度大约为0.3D,是4种情况中最短的,球体所受的压差阻力最小,因此阻力系数在4种情况中也最小.随着间距的增大,上游球体后的最小流向速度分布向中心线靠近,回流区域逐渐增加,上游球体所受的压差阻力也逐渐增大,阻力系数随之增大,如图 11所示.后3种情况的最小流向速度位置位于上游球体后,仅在G=2D时,在下游球体后有一最小流向速度与上游球体相当.间距从G=D增加到G=3D的过程中,流向速度最小值呈先增大后减小的趋势,G=2D时,流向速度最小值是4种情况中最大的,说明流向回流的强度最弱.G=1.5D时,中心线的流向速度皆为负值,说明在此间距条件下,流向回流充满整个区域,下游球体的流向来流速度很小,提前了边界层的分离,增大了压差阻力,导致阻力系数增大.随间距增加,两球体间的相互作用逐渐减弱,下游球体流向来流速度逐渐增大到远前方值,边界层分离逐渐推迟,压差阻力逐渐减小,阻力系数也随之减小.
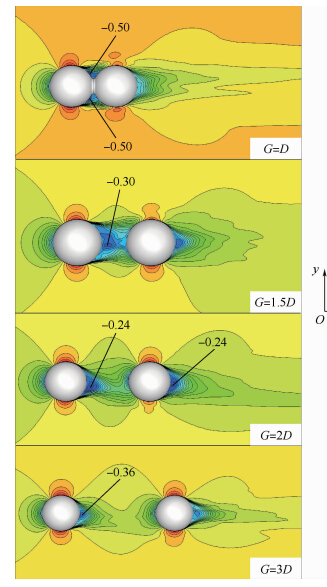 |
| 图 13 不同间距流向无量纲时均速度图 Fig. 13 Patterns of time-averaged streamwise velocity at different spacing |
为了显示尾流中的涡结构,需要采用三维流场的涡识别方法.本文采用Jeong和Hussain的Q-定义方法[16].当G=D时,尾涡结构变化如图 14所示.上游球体的上下面交替脱出“Ω”型涡,下游球体的尾涡结构受上游球体尾涡结构影响,较为复杂.
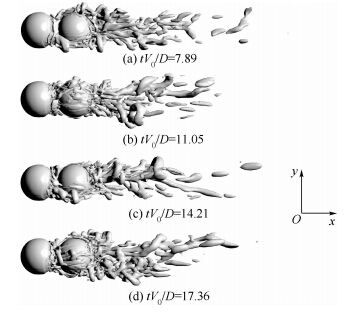 |
| 图 14 G=D时,不同时刻尾涡结构图 Fig. 14 When G=D,the trailing vortex structure at different time |
当G=1.5D时,尾涡结构变化如图 15所示.与G=D时不同,上游球体的尾涡仅从下面脱出,绕过下游球体后有增大趋势.与G=D时相同,下游球体尾涡结构受上游尾涡影响,结构复杂.
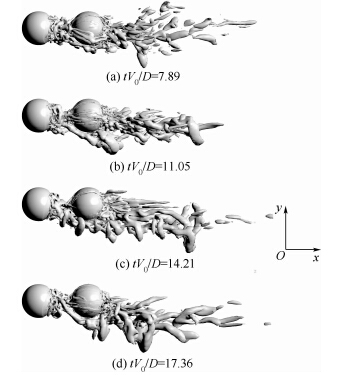 |
| 图 15 G=1.5D时,不同时刻尾涡结构图 Fig. 15 When G=1.5D,the trailing vortex structure at different time |
当G=2D时,尾涡结构变化如图 16所示.相比G=1.5D时,上游球体脱出的尾涡在到达下游球体之前能更充分的发展,两球体间大约有2、3个“Ω”型涡环.
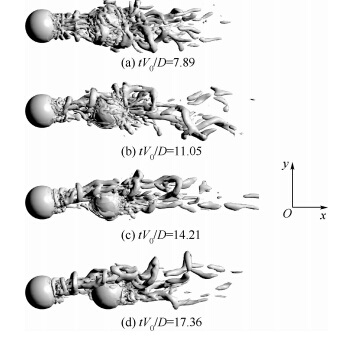 |
| 图 16 G=2D时,不同时刻尾涡结构图 Fig. 16 When G=2D,the trailing vortex structure at different time |
当G=3D时,尾涡结构变化如图 17所示.随着两球间距的加大,上游球体的尾涡结构对下游球体的影响逐渐减弱,下游球体脱出的尾涡结构能够观察到“Ω”型涡环.
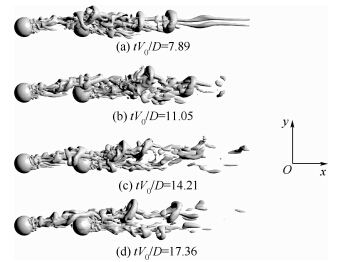 |
| 图 17 G=3D时,不同时刻尾涡结构图 Fig. 17 When G=3D,the trailing vortex structure at different time |
采用大涡模拟法对“球形囊体型”平流层浮空器的气动模型(超临界雷诺数串列双球体)进行了数值研究,得出相关结论,对平流层浮空器的气动设计具有一定的参考意义.
1) 本文方法在分析超临界雷诺数球体绕流问题时具有准确性,可以为“球形囊体型”平流层浮空器气动设计提供参考依据.
2) 随上下游球体间距G增加,上游球体的阻力增大,下游球体的阻力先增大后减小,两球体合阻力先增大后减小,G=D时合阻力最小,G=1.5D时合阻力最大.
3) 随上下游球体间距G增加,上游球体的阻力振动频率逐渐减小.G=D时,下游球体的阻力振动频率略大于上游球体,G=1.5D和G=2D时,上下游球体有相同的占优振动频率,G=3D时,下游球体的占优振动频率为上游球体的6倍.
4) G=D时,在上游球体的侧后方流向回流速度最强,随着间距的增大,上游球体后的最小流向速度分布向中心线靠近,G=1.5D时,流向回流充满中心线附近区域,随间距继续增加,两球体间的相互作用逐渐减弱.
5) G=D时,上游球体的上下面交替脱出“Ω”型涡,随间距增大,上游球体的尾涡仅从下面脱出,当间距达到G=3D时,上游球体的尾涡结构对下游球体的影响较小.
| [1] | Volpe J. Lockheed Martin's HALE-D airship learns to fly makes a crash landing[EB/OL].(2011-07-28).http://www.engadgetcom/2011/07/28/lockheed-martins- hale-d-airship-learns-to- fly-makes-a-crash-la/. |
| Click to display the text | |
| [2] | Sakamoto H, Haniu H.A study on vortex shedding from spheres in a uniform flow[J].Journal of Fluids Engineering,1990,112(4): 386-392. |
| Click to display the text | |
| [3] | Constantinescu G, Squires K.Numerical investigations of flow over a sphere in the subcritical and supercritical regimes[J].Physics of Fluids,2004,16(5):1449-1466. |
| Click to display the text | |
| [4] | Rodriguez I, Lehmkuhl O,Borrell R,et al.Flow dynamics in the turbulent wake of a sphere at sub-critical Reynolds numbers[J].Computers & Fluids,2013,80:233-243. |
| Click to display the text | |
| [5] | Moradian N, Ting D S K,Cheng S.The effects of freestream turbulence on the drag coefficient of a sphere[J].Experimental Thermal and Fluid Science,2009,33(3):460-471. |
| Click to display the text | |
| [6] | Hassanzadeh R, Sahin B,Ozgoren M.Numerical investigation of flow around a sphere[J].International Journal of Computational Fluid Dynamics,2011,25(10):535-545. |
| Click to display the text | |
| [7] | Hassanzadeh R, Sahin B,Ozgoren M.Large eddy simulation of flow around two side-by-side spheres[J].Journal of Mechanical Science and Technology,2013,27(7):1971-1979. |
| Click to display the text | |
| [8] | Pinar E,Sahin B, Ozgoren M,et al.Experimental study of flow structures around side-by-side spheres[J].Industrial and Engineering Chemistry Research,2013,52(40):14492-14503. |
| Click to display the text | |
| [9] | 邹建峰,任安禄, 邓见.圆球绕流场的尾涡分析和升阻力研究[J].空气动力学学报,2004,22(3):303-308. Zou J F,Ren A L,Deng J.Numerical investigations of wake and force for flow past a sphere[J].Acta Aerodynamica Sinica,2004,22(3):303-308(in Chinese). |
| Cited By in Cnki (21) | |
| [10] | 任安禄,李广望, 邹建峰.中等雷诺数圆球绕流的数值研究[J].浙江大学学报,2004,38(5):644-648. Ren A L,Li G W,Zou J F.Numerical study of uniform flow over sphere at intermediate Reynolds numbers[J].Journal of Zhejiang University,2004,38(5):644-648(in Chinese). |
| Cited By in Cnki (8) | |
| [11] | 邹建锋,任安禄. 串列双圆球的流场转捩研究[J].浙江大学学报,2006,40(1):107-112. Zou J F,Ren A L.Study on transitions for flow past two spheres in tandem arrangement[J].Journal of Zhejiang University,2006,40(1):107-112(in Chinese). |
| Cited By in Cnki (21) | Click to display the text | |
| [12] | Germano M, Piomelli U,Moin P,et al.A dynamic subgrid-scale eddy viscosity model[J].Physics of Fluids A:Fluid Dynamics(1989-1993),1991,3(7):1760-1765. |
| Click to display the text | |
| [13] | Wilcox D C. Turbulence modeling for CFD[M].2nd ed.La Caflada,CA:DCW Industries,Inc.,1998. |
| [14] | Achenbach E. Experiments on the flow past spheres at very high Reynolds numbers[J].Journal of Fluid Mechanics,1972,54(3):565-575. |
| Click to display the text | |
| [15] | Jeong J,Hussain F. On the identification of a vortex[J].Journal of Fluid Mechanics,1995,285:69-94. |
| Click to display the text |





