直接序列扩频(DSSS,Direct Sequence Spread Spectrum)信号具有抗干扰、抗噪声、抗多径干扰、低截获、测距性能好和可码分多址等优点,被广泛应用于军事通信、导航和航天测控等领域.扩频通信优越性以精确同步为前提,同步过程一般包括捕获阶段、跟踪阶段2个阶段,其中捕获是首要任务.信号捕获的主要限制因素是载波频率和伪码相位的不确定性.DSSS信号的捕获过程就是在整个多普勒频率和码相位上以固定间隔进行二维搜索,这对接收机的硬件或计算能力提出了很高的要求,尤其是在高动态情况下,长码DSSS信号的快速捕获实现困难,捕获范围和平均捕获时间(MAT,Mean Acquisition Time)是一对相互限制指标[1].为了实现信号的快速捕获,接收机可以采用大量的并行相关器来降低捕获时间,但是随着捕获范围的增大,接收机硬件复杂度也会急剧增大[2].在没有辅助情况下,同时降低相关器个数和捕获时间往往难以实现[3].另外一个选择就是基于快速傅里叶变换(FFT,Fast Fourier Transform)的DSSS信号捕获方法,通过专用数字信号处理器快速地实现大量的假设检验处理,能够降低接收机的硬件资源消耗.基于FFT的捕获方法首先分别对接收信号和本地生成伪码进行FFT变换,然后在频域进行复数相乘,最后对相乘结果进行逆FFT变换,但是也存在计算量大和高动态适应性等问题[4, 5, 6].总之,相对于上述传统信号捕获方法,一种理想的捕获方法应该能够同时降低相关器和计算量需求.
最近,出现了一种新型DSSS信号捕获方法,其采用折叠或双折叠技术[7, 8].折叠技术对本地生成PN码进行折叠处理,降低了MAT,但是会不可避免地引入信噪比(SNR,Signal to Noise Ratio)恶化.为了降低折叠技术带来的SNR恶化,双折叠技术同时对接收信号进行折叠处理,但是MAT会有所增大.
压缩感知(CS,Compressive Sensing)是另一种可能用来实现DSSS信号快捕的新兴技术.CS技术可以利用信号的稀疏性,降低能够完美表达信号所需的采样点数目.从理论上说,CS技术找到了能够解决欠定线性方程组的方法[9, 10, 11].在DSSS系统中,假设扩频伪码序列已知,则接收信号能够被很小的信息表达,即其码相位和多普勒频率.例如,当本地生成信号接近于接收信号时,虽然伪码长度可以为1023,但是如果信号在相关域表示,其稀疏度仅为1,此时信号最稀疏.在传统的DSSS信号捕获方法中,接收机检验N个码相位假设来获取N个测量值,需要N个相关器,而根据压缩感知技术,相关器数量可以远远小于N.因此,DSSS信号捕获可以利用压缩感知技术,以期有效降低所需相关输出测量值个数.应用压缩感知理论,首先必须找到能够最稀疏表达目标信号的稀疏变换矩阵,其次需要寻求合适的测量矩阵及其相对应的有效重构算法.
迄今为止,国内外学者已经提出了多种测量矩阵和重构算法,其中随机Gaussian矩阵和随机Bernoulli矩阵已经在压缩感知中被广泛使用,但是与其相对应的重构算法普遍都有较高的计算复杂度[12].因此,有学者提出了确定性压缩感知技术,该类压缩感知采用确定性测量矩阵,测量矩阵对应的重构算法计算复杂度较低[13].其中,确定性的Walsh-Hadamard矩阵由于具有类似于FFT的快速Walsh-Hadamard变换(FWHT,Fast Walsh-Hadamard Transform)算法而广受关注[14].
基于DSSS信号在其自相关域较强的稀疏性,本文提出了一种双阶段压缩捕获方法,不仅能够同时降低计算复杂度和硬件消耗,而且与折叠、双折叠技术相比,该方法的噪声鲁棒性明显提高.与传统基于并行相关的捕获方法进行对比分析,仿真结果表明双阶段压缩捕获方法在有效降低相关运算量的前提下,可以达到基于并行相关方法的性能水平.
1 DSSS信号模型分析
在扩频测控体制中一般采用调制效率较高的PCM-CDMA-BPSK调制体制,测控数据被伪随机码扩频后再经载波调制后发射.测控基带设备接收到的中频扩频测控信号可表示为
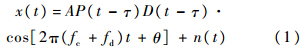
伪码捕获是通过搜索由所有可能的伪码相位和多普勒频率组合构成的二维假设平面,寻找接收信号对应的正确假设,进而得到信号的伪码相位τ和多普勒频率fd,如图 1所示,其中[fmin,fmax]是多普勒频率fd变化范围.假设接收机捕获码相位精度为半个码片之内,采样率(fs)取2倍的伪码速率,即fs=2Rc.
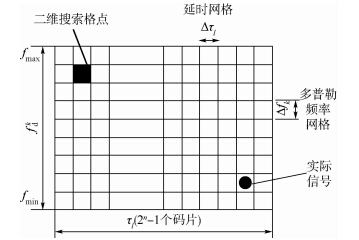 |
| 图 1 多普勒频率与伪码相位二维搜索 Fig. 1 Two-dimensional search for Doppler frequency and pseudo-code phase |
在传统的捕获方法中,接收机首先要通过相关器对接收信号和本地生成参考信号进行相关处理,该本地信号可表示为
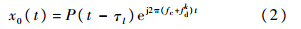
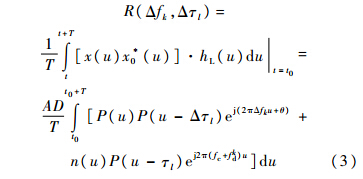
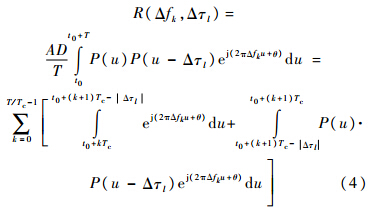
根据式(4)中第2个积分项的积分范围,可知P(u)和P(u-Δτl)相互独立,则该积分项可忽略,并且假设A=1,D=1,式(4)可进一步近似为

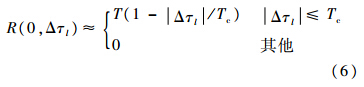
假设接收机采样率fs=2Rc,则式(6)中只有3个连续伪码相位假设可以产生信号相关能量,自相关函数曲线如图 2所示.
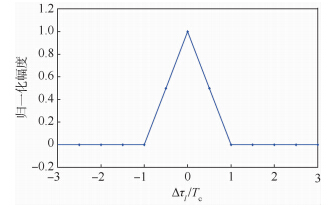 |
| 图 2 自相关函数曲线 Fig. 2 Auto correlation function curve |
根据以上分析可知,DSSS信号在其自相关域内具有较强的稀疏性.假设采样率fs=2Rc,接收信号x={x[0],x[1],…,x[2L-1]}T的稀疏变换矩阵为Ψ,则其构成元素可以表示为
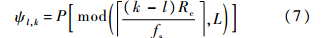
稀疏变换矩阵Ψ能够把接收信号x变换为低稀疏度表示形式,即

式(8)可以等价为2L个并行相关器的相关运算过程,相位分辨率为半个码片.
2 双阶段压缩捕获方法研究
基于第1节DSSS信号模型分析,提出了基于确定性沃尔什-阿达马矩阵的双阶段压缩捕获算法,该算法主要包括2个处理阶段,算法流程图如图 3所示.其中,Φ′1=Φ1Ψ为等效第1阶段测量矩阵,Φ1为第1阶段测量矩阵;Φ′2为等效第2阶段测量矩阵.下面分别加以论述.
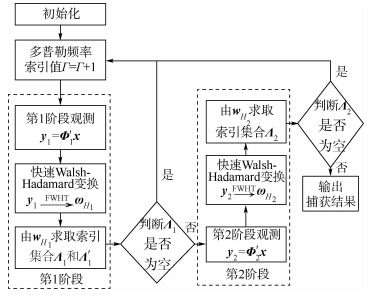 |
| 图 3 双阶段压缩捕获算法流程图 Fig. 3 Two-stage compressive acquisition algorithm flow chart |
2.1 第1阶段压缩测量及检测
基于确定性沃尔什-阿达马矩阵,构造第1阶段测量矩阵Φ1,其构成元素为
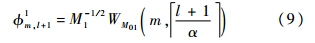
第1阶段测量过程如下:

根据第1阶段的观测向量y1,第1阶段检测算法通过M1点FWHT生成向量wH1,目的是为了寻找最大系数所对应的Walsh码[13].I路和Q路分别进行FWHT,生成相应的向量wH1组成部分,需要2M1lbM1次乘法,并且为了获得WH1=wH12,需要2M1次乘法和2M1-1次加法.因此,第1阶段总共需要2M1(lbM1+1)次乘法.把WH1的每个元素与第1阶段检测门限γ1进行比较,找出大于门限值的Nmax个最大元素,假设这些元素索引由Λ1表示,则有Λ1{0,1,…,M1-1}和Λ10≤Nmax.假设第1阶段检测成功,Λ1的每个元素都可能包含ACF输出的正确峰值位置,由Λ1扩展可得出峰值的所有可能位置的索引集合Λ′1,如下:
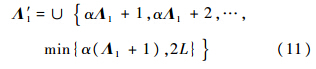
2.2 第2阶段压缩测量及检测
基于第1阶段检测情况,第2阶段需要使用Λ′10个并行压缩相关器检测集合Λ′1中包含的Λ′10个所有可能码相位,寻找y0的ACF输出峰值位置(以半个码片精度),该阶段测量矩阵Φ2的构成元素为
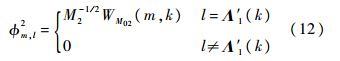
第2阶段测量过程如下:
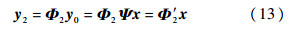
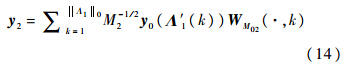
根据第2阶段观测向量y2,第2阶段检测算法通过M2点FWHT生成向量wH2,目的也是为了寻找最大系数所对应的Walsh码.I路和Q路分别进行FWHT,生成相应的向量wH2组成部分,需要2M2lbM2次乘法,并且为了获得WH2=wH22,需要2M2次乘法和2M2-1次加法.因此,第2阶段总共需要2M2(lbM2+1)次乘法.把WH2的每个元素与第2阶段检测门限γ2进行比较,找出大于门限值的最大元素,假设该元素索引为Λ2{0,1,…,M2-1},则Λ′1(Λ2)就是最终捕获的码相位值,并且其捕获精度是半个码片,满足后续的跟踪要求.
3 性能分析
主要从检测概率、平均捕获时间2方面对提出的双阶段压缩捕获方法进行性能分析.
3.1 检测概率
首先给出接收信号信噪比PSNR和稀疏化信号(即相关检测输出)信噪比PSNR0定义,即
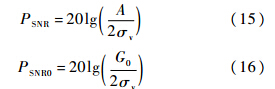
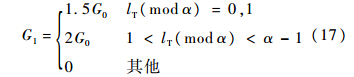
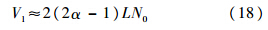
第2阶段中I路和Q路FWHT输出平均幅度分别为G0cosθ和G0sinθ,因此WH2=wH22平均幅值 G2=G0,则第2阶段输出判决量的噪声方差为

当集合Λ1包含lT时,WHi(i∈{1,2})服从两自由度的非中心卡方分布,即
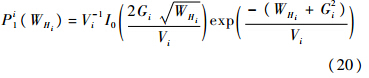
当集合Λ1不包含lT时,WHi(i∈{1,2})服从两自由度的中心卡方分布,即
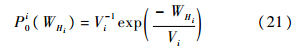
则第1阶段检测概率为
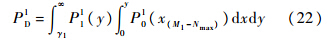
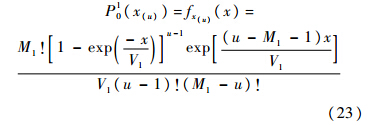
为了简化分析模型,在后续分析中假设Nmax=1,即只考虑双阶段压缩捕获方法的最简单实现情况.根据文献[3]中的推论,可得第1阶段检测概率为
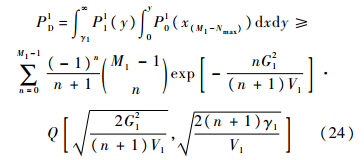
同上,第2阶段检测概率可以表示为
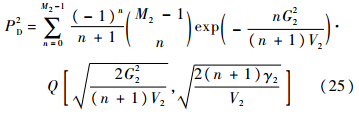
式中M2=α(由Nmax=1易得).根据式(25)可知,由于M22L,在同等输入信号SNR水平下,检测概率P2D要比传统基于并行相关方法的检测概率高.
综合式(20)、式(21)和文献[3]的推论,可得漏报概率和虚警概率分别为

注意,双阶段压缩捕获方法与传统基于并行相关方法的P1D,P1M和P1F拥有相同的表达式,只是具体参数有所不同,这和预期结果保持一致,因为2个阶段测量值y1和y2可以看作是对相邻相关器输出的有效合并.在输入信号SNR相同条件下,双阶段压缩捕获方法可以用较少的相关运算获得与传统基于并行相关方法相同的性能水平.
3.2 平均捕获时间
忽略很小的FWHT计算时间,假设第1、第2阶段测量值y1,y2的获取时间都是T1=LTc,验证模式时间为TV=N2LT1,信号捕获的环形搜索状态转移流程图如图 4所示.
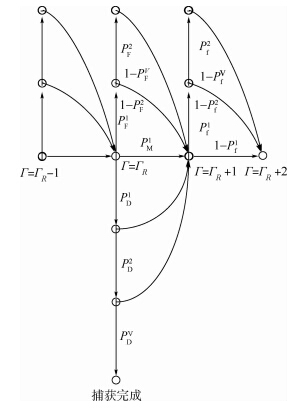 |
| 图 4 环形搜索状态转移流程图 Fig. 4 Circular search state shift diagram |
如果当前多普勒频率假设fΓ最接近多普勒频率真实值fd,第1阶段检测结果存在成功检测、漏报和虚警3种可能情况.如果第1阶段检测漏报,多普勒频率假设Γ加1,在下个节点重复第1阶段检测过程.如果第1阶段成功检测或虚警,则启动第2阶段检测.如果第2阶段成功检测,则启动验证模式.直接正确假设检验(从节点Γ=ΓR到完成捕获)、正确假设漏报(从节点Γ=ΓR到节点Γ=ΓR+1)和非正确假设检验(从节点Γi到节点Γi+1,且i≠R)3种情况的传递函数分别为
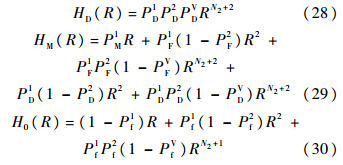
在实际中,验证模式函数多采用N1-N2检测器[16],其检测概率和虚警概率分别为
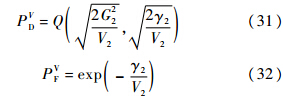

注意,在式(34)中忽略了第1阶段的成功检测,而第2阶段出现虚报、虚警及第2阶段成功检测,而验证模式出现虚报、虚警2种情况.上述假设在一般情况下,尤其是较高SNR条件下,具有合理性.根据文献[2]结论,系统传递函数可表示为
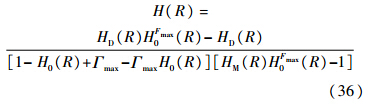
根据系统传递函数与MAT相互关系μR=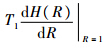 ,可得系统的MAT为
,可得系统的MAT为
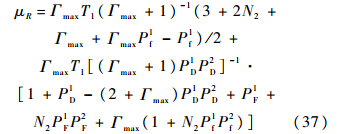
当SNR较低时,P1DP2D降低,式(37)的第2项会增加,从而导致平均捕获时间μR增加.当信噪SNR较高时,式(37)可以简化为
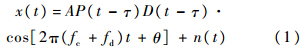
式(38)表明,MAT与第1、第2阶段测量值y1,y2的获取时间、验证模式时间和多普勒频率搜索容限等因素成正比.
4 仿真校验
对双阶段压缩捕获方法进行蒙特卡罗实验验证,主要思路是从检测概率和平均捕获时间出发,对比分析双阶段压缩捕获方法和传统基于并行的相关方法的捕获性能.仿真实验参数设置如下:考虑BPSK调制DSSS信号,数据率Rb=1kb/s,码速率Rc=10MHz,采样率fs=2Rc,多普勒频率fd=100Hz,码相位τ=1000,相关处理时间1ms,即2L=2046个采样值,第1和第2阶段捕获门限分别为γ1=1.2和γ2=0.75[3].
4.1 检测概率
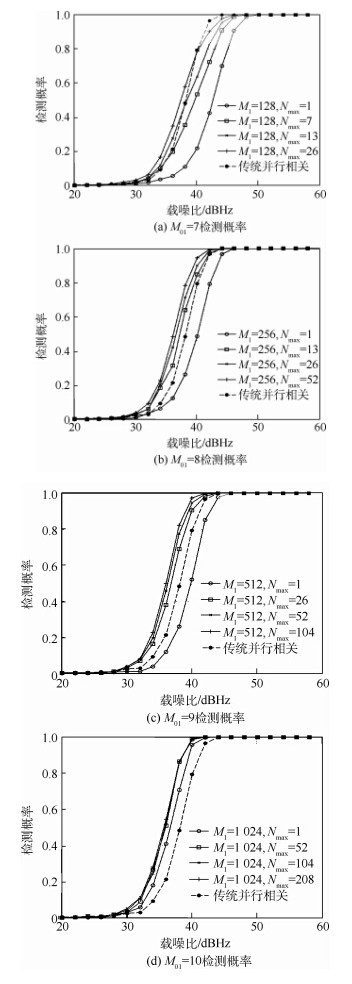
在不同测量值个数情况下,通过蒙特卡洛仿真对比分析双阶段压缩捕获方法与传统基于并行相关方法的检测概率,其中载噪比C/N0变化范围取[20, 60]dBHz,测量矩阵Φ1与Φ2构造参数分别为M01∈{7,8,9,10}和M02=lb(2L/M1),则有第1阶段测量值个数M1∈{128,256,512,1024},第1阶段超过门限的最大值个数Nmax∈{1,0.05M1,0.1M1,0.2M1},检测概率对比如图 5所示.
 |
| 图 5 检测概率对比 Fig. 5 Comparison of detection probability |
由图 5可知,仿真结果与理论分析结果基本吻合,检测概率随着第1阶段测量值个数M1和超过门限的最大值个数Nmax增加而增大,并且最终趋向于一个稳定值.当M1=256且Nmax=13时,双阶段压缩捕获方法捕获性能与传统基于并行相关方法的基本持平,且有α≈2L/M1=8,第1和第2阶段的相关次数分别为256和αNmax=104,即双阶段压缩捕获方法相关次数总共为360,而传统基于并行相关的方法相关次数为2L=2046,可知此时双阶段压缩捕获方法相关次数相对于传统基于并行相关的方法几乎降低了6倍,说明双阶段压缩捕获算法在显著降低相关运算量的前提下,能够达到传统基于并行相关捕获方法的检测概率水平.
4.2 平均捕获时间
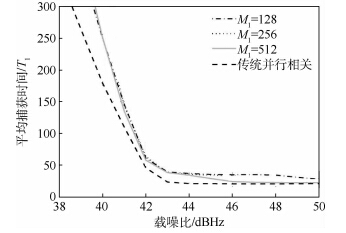
实验条件设置与检测概率实验条件设置基本相同,测量矩阵Φ1构造参数取M01∈{7,8,9},即第1阶段测量值个数M1∈{128,256,512},第1阶段超过门限的最大值个数Nmax=4α,测量值获取时间T1=1ms,N2=10,Γmax=20,平均捕获时间对比关系如图 6所示.
 |
| 图 6 平均捕获时间对比关系 Fig. 6 Comparison of MAT |
由图 6可知,在载噪比较高(>42dBHz)时,双阶段压缩捕获方法平均捕获时间趋向于一个稳定的最小值22T1,该最小值与式(38)得到的理论值2T1+10T1+(20/2)T1相一致;在载噪比较低时,双阶段压缩捕获方法平均捕获时间随着载噪比的降低而快速增加,这也与3.2节的理论分析保持一致,对应于式(37)的第2项,当载噪比较低时,分母P1DP2D降低,分子1+P1D-(2+20)·P1DP2D+P1F+10P1FP2F+20(1+10P1fP2f)增高,导致平均捕获时间增加.值得注意的是,双阶段压缩捕获方法平均捕获时间的变化趋势与基于传统并行相关方法的保持一致,而且第1阶段测量值个数M1越大,双阶段压缩捕获方法平均捕获时间越能够较快地接近基于传统并行相关方法的平均捕获时间.
5 结 论
基于压缩感知理论,提出了一种双阶段压缩捕获方法,并进行了理论分析与实验对比验证,主要结论有:
1) 在显著降低相关运算量的前提下,该方法能够达到传统基于并行相关捕获方法的检测概率水平.
2) 该方法平均捕获时间的变化趋势与基于传统并行相关方法的保持一致,而且第1阶段测量值个数越大,双阶段压缩捕获方法平均捕获时间越能够较快地接近基于传统并行相关方法的平均捕获时间.
3) 双阶段压缩捕获方法能够有效利用DSSS接收信号在自相关域的稀疏性,可以有效解决DSSS信号在捕获过程中难以同时实现的高检测性能、低硬件消耗或计算量问题.
| [1] | 田日才. 扩频通信[M].北京:清华大学出版社,2006:1-26. Tian R C.Spread spectrum communication[M].Beijing:Tsinghua University Press,2006:1-26(in Chinese). |
| [2] | Huang Z J, Zhou J,Chen B,et al.A novel two-dimensional space-time processing scheme for DS/CDMA code acquisition[C]//International Conference on Signal Processing,Communication and Computing.Kunming:IEEE,2013:1-6. |
| [3] | Myeongsu H, Takki Y,Kang C,et al.A new adaptive code-acquisition algorithm using parallel sub filter structure[J].IEEE Transactions on Vehicular Technology,2006,55(6):1790- 1796. |
| Cited By in Cnki (0) | Click to display the text | |
| [4] | Wu H B, Hu Y H.Fast acquisition of GPS signal in low SNR environments[C]//The 2nd International Conference on Information Science and Engineering.Hangzhou:IEEE,2010:4534-4537. |
| [5] | Liu S X, Feng W Q,Xiong H G,et al.A FFT based long-code acquisition algorithm suitable for FPGA implementation[C]//2011 International Conference on Electric Information and Control Engineering.Wuhan:IEEE,2011:5621-5624. |
| [6] | Hong L. Research on global positioning system M-code acquisition method and the acquisition performance[J].IET Communications,2014,8(5):587-596. |
| Cited By in Cnki (0) | Click to display the text | |
| [7] | Tian M H, Feng Y X,Liu F.On the scheme of rapid acquisition of long PN code in DSSS Signals[C]//The 5th International Conference on.Kunming:IEEE,2009:457-460. |
| [8] | Li H,Cui X, Lu M,et al.Dual-folding-based rapid search method for long PN-code acquisition[J].IEEE Transactions on Wireless Communication,2008,7(12):5286-5296. |
| Cited By in Cnki (0) | Click to display the text | |
| [9] | Feng W Q. Dual-channel method for fast long PN-code acquisition[J].Communications,China,2014,11(5):60-70. |
| Cited By in Cnki (0) | Click to display the text | |
| [10] | Candes E J, Tao T.Decoding by linear programming[J].IEEE Transactions on Information Theory,2005,51(12):4203-4215. |
| Cited By in Cnki (0) | Click to display the text | |
| [11] | Donoho D L. Compressive sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306. |
| Cited By in Cnki (0) | Click to display the text | |
| [12] | Candes E J, Wakin M B.An introduction to compressive sampling[J].IEEE Signal Processing Magazine,2008,25(2):21-30. |
| Cited By in Cnki (0) | Click to display the text | |
| [13] | Calderbank R, Howard S,Jafarpour S.Construction of a large class of deterministic sensing matrices that satisfy a statistical isometry property[J].Selected Topics in Signal Processing,2010,4(2):358-374. |
| Cited By in Cnki (0) | Click to display the text | |
| [14] | Ouyang W L. Fast algorithm for walsh hadamard transform on sliding windows[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2010,32(1):165-171. |
| Cited By in Cnki (0) | Click to display the text | |
| [15] | Sofotasios P C, Freear S.Novel expressions for the Marcum and one dimensional Q-functions[C]//7th International Symposium on Wireless Communication Systems.York:IEEE,2010:736-740. |
| [16] | Ward P W. GPS receiver search techniques[C]//IEEE Position Location and Navigation Symposium.Atlanta:IEEE,1996:604-611. |





