Download PDF  
文章快速检索  
  高级检索
引用本文
付子豪, 龚光红. 矩的显式积分算法研究与应用[J]. 北京航空航天大学学报, 2015, 41(4): 727-731
FU Zihao, GONG Guanghong. Explicit moment integration algorithm and its application[J]. Journal of Beijing University of Aeronautics and Astronsutics, 2015, 41(4): 727-731.
矩的显式积分算法研究与应用
付子豪, 龚光红    
北京航空航天大学 自动化科学与电气工程学院, 北京 100191
收稿日期:2014-05-13; 录用日期: 2014-08-25; 网络出版日期: 2014-10-15
作者简介: 付子豪(1990—),男,四川德阳人,硕士生,fuzihaofzh@gmail.com
通讯作者: 龚光红(1968—),女,四川石柱人,教授,ggh@buaa.edu.cn,主要研究方向为分布仿真与虚拟技术.
摘要：矩的求解通常被用于求解有限元、体积、惯性矩等问题中.基于矩的叠加性,首先给出了在三维空间中计算域的离散方式,并推导了矩的显式积分公式,随后将其推广到n维空间中,该表达式易于在计算机上实现;设计了矩的并行计算算法,并通过Fortran和Python混编的方式,实现了矩的并行计算;对多重精度下的样例数据给出了一个算例,实现了零阶矩和二阶矩的计算,并和串行算法、逐次降维算法作出比较,进行了效率分析和误差分析.结果显示,矩的显式积分并行计算算法易于程序实现,并且在效率上高于串行算法,能够很容易推广到高维空间,该算法具有高度可并行性,误差主要来自计算域离散.
关键词： 矩     显式积分公式     并行计算     逐次降维     计算域离散    
Explicit moment integration algorithm and its application
FU Zihao, GONG Guanghong     
School of Automation Science and Electrical Engineering, Beijing University of Aeronautics and Astronautics, Beijing 100191, China
Abstract:The calculation of moment is often used in finite element method, volume calculation, moment of inertia calculation, etc. A discrete method of the computational domain in three-dimensional space was proposed firstly based on the superposition of moment. An explicit formula was derived in three-dimensional space and then extended to n-dimensional space, which can be easily implemented on the computer. Secondly, a parallel algorithm of moment calculation was designed and implemented with mixed Fortran and Python. Thirdly, a zero-order and second-order moment was calculated in a multi-fidelity example. The efficiency of the algorithm was compared with a serial algorithm and a successive dimensionality reduction algorithm. Meanwhile, efficiency analysis and error analysis were presented. The result shows that the explicit moment integration algorithm can be easily implemented with programs and runs faster than the serial algorithm. It is highly parallel and can also be easily extended to a higher dimensional space. The algorithm is highly parallel, whose error mainly comes from the discrete process of the computational domain.
Key words: moment     explicit moment formula     parallel computing     successive dimensionality reduction     discrete computational domain    

在采用有限元方法[1]进行刚度矩阵计算、求解物体体积、求解物体的惯性矩[2, 3, 4]等各种力学参数时,常常需要涉及矩的计算.Soerjadi等[5]给出了在二维平面情况下的计算公式.该公式基于格林公式的一个特例得到,令格林公式中,向量场函数的任意一项恒为0,导出将面积分转化为线积分的通式,然后将线积分用空间已知点的值表示出来,继而得出面积分的值.然而,该方法要求向量场函数面积分项中只有一项,且该项需含有对空间所有维度的微分项,因此在三维或更高维度的空间中,无法继续用该方法得到结果.

Johnson和Mirtich等[1, 6]提出了在三维空间进行体积矩积分的方法.该方法首先对于给定的标量场函数构造了一个向量场函数的散度形式,然后通过高斯公式将该向量场函数的散度转化为向量场在计算域表面的积分,随后将该积分拆写成标量场积分的形式,实现了将三维的体积矩转化为二维的面矩,随后再通过斯托克斯公式将面矩的积分转化为线积分和低阶面矩的和的形式,通过递归,得出计算域的矩.虽然该方法解决了三维空间中体积矩的计算问题,但是仍存在几点不足.首先,在通过斯托克斯公式将面矩转化为线积分与低阶面矩和的形式的时候,推导非常复杂;其次,过多地使用了递归计算,在程序实现上会增大运行时的开销;最后该方法只适用于三维空间中的体积矩,对于高维空间中的矩无法计算得到.

Sheynin等[7, 8, 9]给出了求解计算域任意阶矩的公式.并将其推广到了高维空间,该方法未使用降维或递归的手段,而是直接给出了矩的显式表达式,降低了问题的复杂度.然而该表达式不便于计算机实现.

本文在Sheynin等基础之上推导了n维空间中的便于计算机程序实现的矩的显示公式.并基于在三维空间的公式,使用Python与Fortran混编的技术,实现了三维空间下矩的计算,并以Boeing777-200LR为例,给出了一个算例,评估了并行计算的效能,并和逐次降维法进行了对比.

1 矩的定义与公式推导 1.1 矩的定义及物理意义

首先给出矩的定义,如式(1)所示,以下就该公式的计算进行讨论.

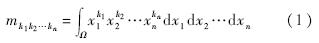
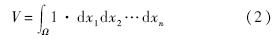
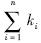式中,x1,x2,…,xn为n维空间中的坐标;mk1k2…kn为在x1,x2,…,xn上的k1,k2,…,kn阶矩;Ω为积分计算域.当k1=k2=…=kn=0时,mk1k2…kn具有体积的物理意义,公式如下:
而当=2时,mk1k2…kn具有惯性矩的物理意义,简单起见,考虑三维空间中刚体的惯性矩张量I,有
式中，对角线上的Ixx,Iyy,Izz分别为在x,y,z轴上的转动惯量,其定义如下所示:
而非对角元素则是惯量积,定义如下所示:

由上可见,体积和惯性矩都可以通过矩积分的方式来获取.下面先给出三维空间中矩的公式以及推导过程,随后将其推广到n维空间中.

1.2 计算域的分割

对于不规则计算域的通式推导是困难的.因此本文首先将任意形状的计算域进行分割,将整个计算域(Ω)转化为若干个三角形包围的多面体,再在这若干个四面体中进行计算,最后将结果叠加.在进行四面体矩的计算时,通过坐标变换的方法在顶点为原点、3条棱与坐标轴重合且长度为1的四面体(称作标准四面体)上进行计算,从而得到任意四面体的矩.

对于空间中的任意计算域,首先将其几何外形用三角形面片进行近似离散,对于每一个三角形,将其3个顶点与原点相连,便能够得到若干以三角形为底,以原点为顶点的四面体,如图 1所示.本文定义四面体和原点相接的3条棱的另一个端点的次序和三角形表面法向量满足右手定则,然后分别在每一个四面体上进行积分,得到每一个四面体的矩,然后将这些四面体的矩相加,由于有方向的定义,所有集合体外部的矩都会被抵消,因此所有四面体矩的和即是计算域的矩.令T表示用三角化离散后的计算域,在T中,有r个顶点在原点的四面体,记作Ti,有

图 1 空间四面体的定义Fig. 1 Definition of tetrahedron
图选项
1.3 n维空间下标准四面体公式

首先推导在n维空间下的标准四面体的计算公式.n维空间标准四面体积分定义为

式中,x1,x2，…，xn≥0,x1+x2…+xn≤1.

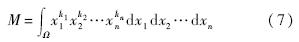
使用Dirichlet积分公式有

式中,Γ(n)表示伽马函数,定义为Γ(n)=(n-1)!.

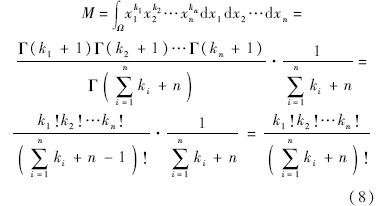
1.4 三维空间任意四面体的矩

对于三维空间中任意四面体的矩,可以采用直接积分的方法来得到.首先,选取四面体与原点相接的3条棱为新的坐标系,将四面体用它的3条边表示,记作T(a,b,c),其中a,b,c都是列向量,且a=(a1,a2,a3)T,b=(b1,b2,b3)T,c=(c1,c2,c3)T,从而得到从旧坐标到新坐标的变换矩阵(a,b,c)－1,记作A,其中的元素为{aij},在旧坐标系下变量用xi表示,而新坐标系下的变量用yi表示,则坐标转换关系为x=Ay.

记体积矩为mk1k2k3(T),i,j,k为直角坐标系的基,将向量x用Ay替换,即,有

式中，(Ay)(i)代表向量Ay的第i个分量.
这里,使用到了多项式展开定理.式中,表示对所有满足ki1+ki2+ki3=ki的组合进行求和[10].再代入标准四面体矩公式得：
1.5 矩公式在高维空间的推广

将三维空间的通式向高维空间推广,容易得到高维空间中的矩公式:

式中，表示n个求和号累加的形式.由于多重求和号可以通过多重循环实现,因此该形式易于计算机程序设计.

2 矩的并行计算算法

在第1节中,推导了三维空间下任意矩积分的公式.在本节,基于该公式设计出矩的并行计算算法,并对并行、串行显式积分公式算法和Mirtich[6]提出的逐次降维法进行比较.

2.1 矩的并行显式积分公式算法

由计算域的分解可知,矩的计算需要求出n个四面体的矩,然后将其相加,而这部分计算是相互间没有关联的,因此,可以通过并行计算的方法来实现,实现原理如图 2所示.

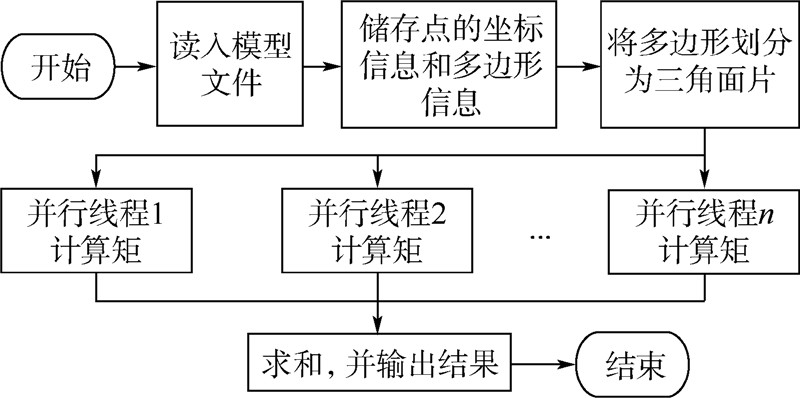图 2 并行算法流程图Fig. 2 Flowchart of parallel algorithm
图选项

本次计算采用Boeing777-200LR的三角化表面网格(图 3)作为测试几何体.通过设置不同的三角剖分精度,得到了不同层级的网格.通过对单位密度几何体的零阶矩∫Ω1dm和二阶矩∫Ωy2dm的计算,比较了3种方法的效率.

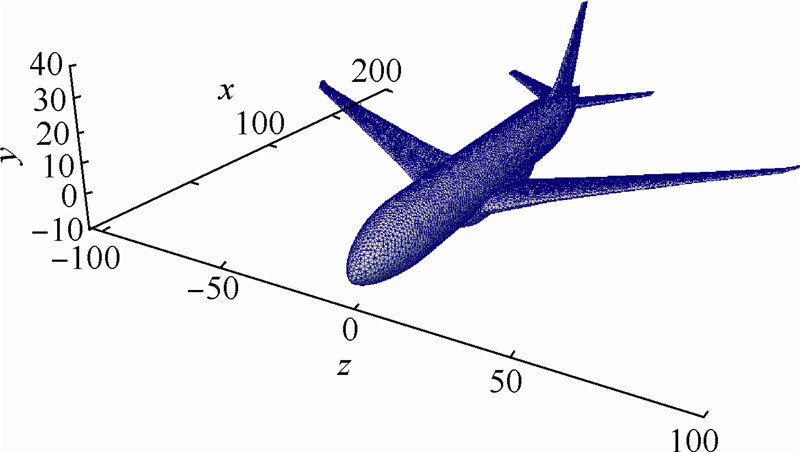图 3 几何体表面三角网格Fig. 3 Surface triangular mesh of geometry
图选项

为了简化几何处理的复杂度,该程序使用Python[11, 12]做外部接口;为了提升计算速度,实现并行计算,采用Fortran做底层计算,并行的部分也由Fortran来实现.并行的部分通过在Fortran代码中加入OpenMP[13, 14],将循环自动地分配到各个CPU上,提高计算效率.计算环境使用IntelCoreTM i7-3770 CPU主频3.4 GHz 4核8线程8 GB RAM.

2.2 结果分析

通过对不同精度的Boeing777-200LR网格[15]进行计算,结果如图 4和表 1所示.

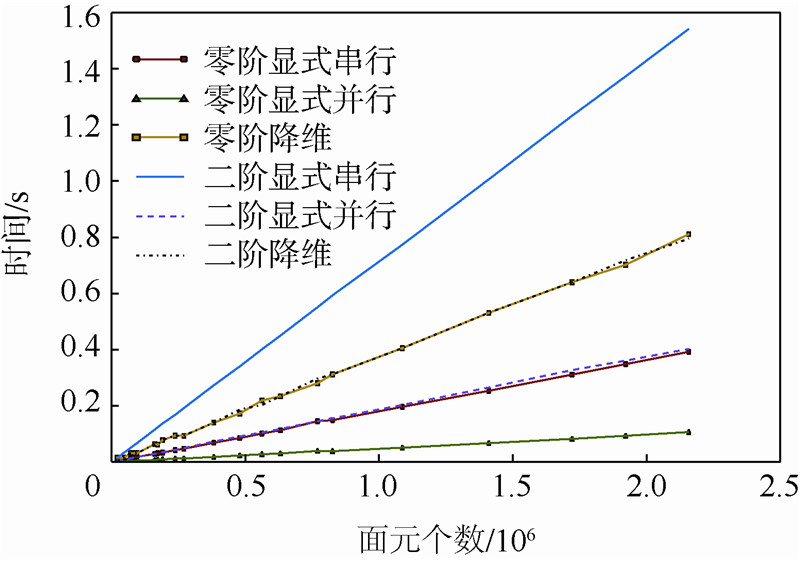图 4 算例结果分析Fig. 4 Example results analysis
图选项
表 1 计算结果 Table 1 Calculation results
单元数零阶矩二阶矩
显式积分公式法逐次降维法显式积分公式法逐次降维法
矩/kg串行时间/ms并行时间/ms矩/kg时间/ms矩/(kg·m2)串行时间/ms并行时间/ms矩/(kg·m2)时间/ms
205 2466 3733266 373162 004 1121602 004 1120
269 94866 689471266 689932 024 921109472 024 92694
478 99066 700852366 7001722 025 507218632 025 511187
631 22866 7041133066 7042342 025 687281932 025 692234
769 50666 7051453966 7052802 025 7903431092 025 795297
1 087 33666 7081965166 7084052 025 9764991562 025 982405
1 721 68266 7103118266 7106402 026 1087642342 026 113640
2 158 23266 71139210666 7118112 026 1549672502 026 159795
表选项

在该算例中,分别通过串行和并行的显式积分公式算法,计算了几何体的零阶和二阶矩,并和逐次降维法做了对比.可以看出,随网格数的增大,计算时间线性增加;在同等情况下,并行效率大致为串行效率的3.7倍;在计算零阶矩时,显式积分公式法效率高于逐次降维法,而当矩的阶数增大时,逐次降维法的效率较高,但仍低于并行的显式积分公式法;显式积分公式法能很快推广到高维空间,而逐次降维法仅限于三维空间中.

在程序并行计算时,由于CPU 4核8线程一个核上的两线程存在干扰,不便于比较效率,因此在这里关闭CPU的超线程功能进行测试,相当于4核并行,效率达到了3.7倍左右,由于OpenMP运行的资源消耗,不能达到理想中4倍的运行效率.

对比矩的计算结果误差可知,矩的积分误差主要发生在几何体的离散过程中.随着网格数增加,矩的值同时增大,而最后趋于收敛,对比第1组计算结果和最后一组计算结果,有4.5%的误差,这是由于离散网格随网格数的增加而逐渐贴近于真实边界.其次,对比显式积分公式算法和逐次降维法在相同离散网格下的结果可知,由离散求和造成的矩计算的误差小,其数量级约在10-6左右.其原因是离散几何体矩的计算直接用公式表出,因此其计算误差只表现有限数值精度导致的舍入误差上.综上,矩积分计算的误差主要由几何体离散导致,在实际计算时,需要采用合适的离散网格数进行离散.

3 结 论

通过分析和计算表明:

1) 将计算域用三角面片离散的方式,能有效地将任意计算域转为多面体,简化了计算;

2) 显式积分公式利于在计算机上实现,能方便地推广到高维空间,逐次降维法无法推广;

3) 随着面元数量的增加,并行和串行计算消耗时间都随之线性增长,在测试计算机上并行计算的效率约为串行效率的3.7倍;

4) 矩的计算结果随着网格的细化而逐渐趋于收敛.

参考文献
[1] Johnson F T, Samant S S,Bieterman M B,et al.TRANAIR-a computer code for transonic analyses of arbitrary configurations,NASA-CR-4348[R].Washington,D.C.:NASA,1987.
Click to display the text
[2] 洪国雄. 惯性张量的物理意义[J].大学物理,1989,12(1):7-8. Hong G X.The physical meaning of the inertia tensor[J].College Physics,1989,12(1):7-8(in Chinese).
Cited By in Cnki (1)
[3] 秦莉,杨明, 郭庆.遗传算法在质量矩导弹姿态控制中的应用[J].北京航空航天大学学报,2007,33(7):769-772. Qin L,Yang M,Guo Q.Movingmass attitude control law based on genetic algerithm[J].Journal of Beijing University of Aeronautics and Astronautics,2007,33(7):769-772(in Chinese).
Cited By in Cnki (10)
[4] 徐水源. 惯性矩与惯性张量的关系[J].黄石教育学院学报,2005,22(4):90-92. Xu S Y.The relationship of the moment of inertia and inertia tensor[J].Journal of Huangshi Education College,2005,22(4):90-92(in Chinese).
Cited By in Cnki (5)
[5] Soerjadi R. On the computation of the moments of a polygon,with some applications[M].Netherlands:Stevin Laboratory,1968:43-58.
[6] Mirtich B. Fast and accurate computation of polyhedral mass properties[J].Journal of Graphics Tools,1996,1(2):31-50.
Click to display the text
[7] Sheynin S, Tuzikov A,Vasiliev P.Efficient computations of body moments[J].Информационные Процессы,2002,2(1):22- 23.
[8] Sheynin S A, Tuzikov A V.Explicit formulae for polyhedra moments[J].Pattern Recognition Letters,2001,22(10):1103- 1109.
Click to display the text
[9] Tuzikov A V, Sheynin S A,Vasiliev P V.Computation of volume and surface body moments[J].Pattern Recognition,2003,36(11): 2521-2529.
Click to display the text
[10] Hall M. Combinatorial theory[M].New York:John Wiley & Sons,1998:166.
[11] VanRossum G, Drake F L.Python language reference manual[M].United Kingdom:Network Theory,2003.
[12] VanRossum G, Drake F L.The python language reference[M].Beaverton,OR,USA:Python Software Foundation,2010.
[13] Chandra R. Parallel programming in OpenMP[M].San Francisco:Morgan Kaufmann,2001.
[14] Dagum L, Menon R.OpenMP:an industry standard API for shared-memory programming[J].Computational Science & Engineering,IEEE,1998,5(1):46-55.
Click to display the text
[15] Fredericks W J, Antcliff K R,Costa G,et al.Aircraft conceptual design using vehicle sketch pad[C]//48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition.Reston:American Institute of Aeronautics and Astronautics Inc,2010:1-17.
Click to display the text
http://dx.doi.org/10.13700/j.bh.1001-5965.2014.0266
北京航空航天大学主办。
0

文章信息

付子豪, 龚光红
FU Zihao, GONG Guanghong
矩的显式积分算法研究与应用
Explicit moment integration algorithm and its application
北京航空航天大学学报, 2015, 41(4): 727-731
Journal of Beijing University of Aeronautics and Astronsutics, 2015, 41(4): 727-731.
http://dx.doi.org/10.13700/j.bh.1001-5965.2014.0266

文章历史

收稿日期：2014-05-13
录用日期: 2014-08-25
网络出版日期: 2014-10-15

相关文章

工作空间