表1(Table 1)
为解决常规推力航天器编队的不足(推进剂的消耗影响编队飞行的寿命;推力器排出的羽流可能会对邻近航天器造成冲击,或对其光学器件造成污染,影响成像等),人们提出了采用电磁作用系统,通过航天器之间电磁力及电磁力矩来实现编队控制[1].
电磁航天器的研究始于2000年[1],Miller和Kong[2, 3, 4]等首先提出了电磁编队飞行的概念,对其优点、理论基础、实施方案、可行性及设计等进行了分析.文献[5]建立了近地轨道电磁编队动力学模型,设计了自适应姿轨控制律.文献[6]考虑电磁编队位置跟踪的输入延时和扰动不确定因素,设计了滑模变结构控制律.杨乐平等[7, 8, 9]对电磁编队保持及构型稳定性进行了研究.文献[8]基于Kane方法建立了双星电磁编队6自由度姿轨耦合动力学模型,分析了构型稳定性.文献[9]分析了三星电磁编队相对构型及稳定性.文献[10]基于人工势能函数方法,对电磁编队运动轨迹的规划与控制进行了研究.Inampudi等[11, 12]给出了近地轨道和拉格朗日点附近的双星库仑编队动力学模型,对编队轨迹优化进行研究.2013年,SPPL实验室建立了共振感应近场产生系统(RINGS，Resonant Inductive Near-field Generation System),在国际空间站进行了在轨实验,验证了电磁力推进和无线能源传送技术[13, 14].
本文建立双星电磁航天器“绳系”动力学,并对其构型稳定性及保持进行分析,将电磁编队重构转化为运动规划问题,提出序列控制策略来解决高非线性多星电磁编队问题,最后通过多星电磁编队仿真验证模型及控制的有效性.
1 电磁航天器编队动力学模型 1.1 电磁系统模型电磁航天器通过安装一套三轴正交通电线圈,改变线圈电流产生电磁作用力,来实现航天器编队相对位置控制.基于电磁远场模型,电磁航天器B 在l 位置处产生的磁场强度[5]为
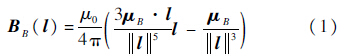
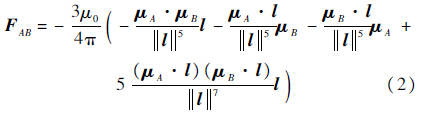
由电磁力解算线圈磁矩是一个复杂的非线性问题,一般可以通过添加约束来简化计算:固定某个电磁航天器的磁矩(如使μB始终沿着AB连线方向,大小保持不变)或者限制双星能量消耗均衡(如使μA=μB,则存在解析解).
电磁力和电磁力矩是耦合产生的,会引起电磁航天器姿轨耦合.为了突出研究电磁编队构型重构问题,本文暂不考虑姿态耦合,认为已通过其他姿控技术保证姿态稳定或机动任务.
1.2 双星电磁航天器相对动力学建模在不考虑地磁场和其他摄动影响的情况下,星间电磁力属于内力,电磁控制不会改变系统质心位置,假设编队系统质心保持Kepler轨道运行.
如图 1所示,春分点地心惯性坐标系记作Si;编队质心第2轨道坐标系记作So;“绳系”坐标系St固连在电磁航天器A,B间假想的系绳上,可由So系先绕y轴转α角,再绕x轴转β角得到(将A,B看作质点,忽略zt轴的旋转变化).相关位置矢量rOc,rA,rB等定义见图 1.So系到St系坐标变换矩阵为
Lto=Lx(β)Ly(α)
 |
| 图 1 电磁航天器编队几何关系示意图Fig. 1 Geometric model of EMFF system |
设编队系统拉格朗日函数为
L=T-Vg-Ve
式中，T为动能;Vg为重力势能；Ve为电磁场势能.取广义坐标q=[α β l]T,拉格朗日动力学方程为
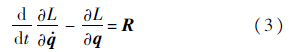
A,B相对系统质心位置矢量为l1和l2,质量为m1和m2,满足m1l1+m2l2=0,令l=l1-l2;即可得l1及l1在So系下相对变化率为
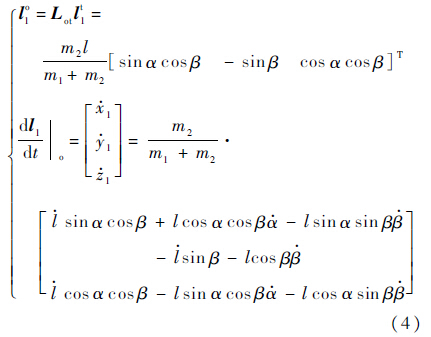
根据速度合成定理,A的绝对运动速度为
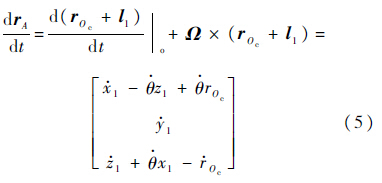
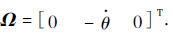
同理可求出B的绝对速度,双星电磁航天器编队系统的动能可以整理为
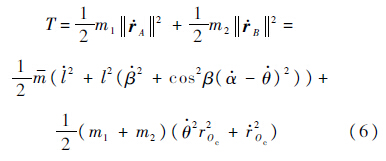
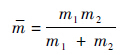
系统重力势能(泰勒展开,保留二阶项)为
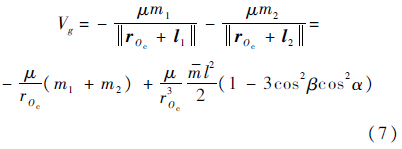
编队系统电磁场势能为
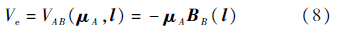
由式(3)可整理得双星电磁航天器近地编队相对动力学模型为
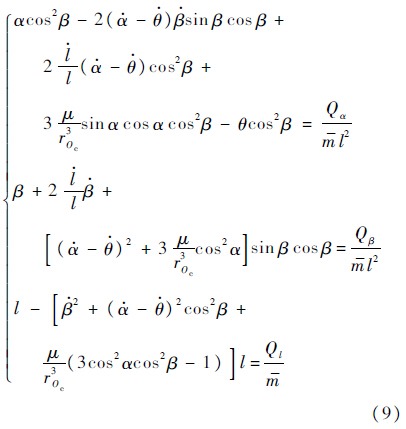
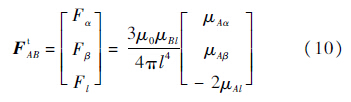
系统模型式(9)具有强非线性和耦合性,使得分析控制过程较为复杂.但是式(9)具有以下优势:
1) 以双星电磁航天器编队构型参数α,β,l为变量,有利于分析编队整体构型的变化规律.由α,β定义,可得双星“绳系”系统相对于So系的角速度为
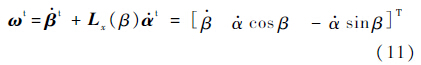
2) 可用于电磁航天器绳系编队分析.
前文建模过程中,双星电磁航天器间并不存在真实的系绳的连接.双星间若存在真实系绳连接,式(9)中第3个关于l式可由绳系装置进行解耦:可以减少绳系方向电磁消耗,节约电能;便于构型重构与保持控制;电磁双星交会过程中,距离过近,电磁远场模型误差较大,可利用系绳低速拉回,完成交会任务.
2.2 模型线性化与稳定性分析
考虑α,β和l存在小偏差:
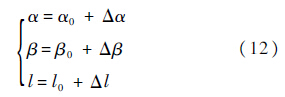
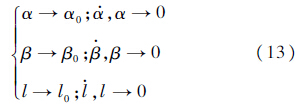
为便于系统径向编队保持(α0=0°,β0=0°,l=l0)稳定性分析与控制,将式(12)代入式(9),泰勒展开进行线性化可得:
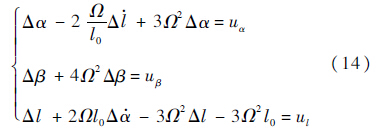
显然,式(14)中,Δβ是解耦的,其零控状态临界稳定;Δα和Δl相耦合,其零控特征方程为λ4+4Ω2λ2－9Ω4=0,可得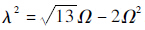
.近地轨道恒有λ2>0,则λ存在实部为正的根.
根据李雅普诺夫线性化定理,可得原系统径向编队构型不稳定.需要设计控制律来保持构型稳定.对式(14)选取反馈控制:
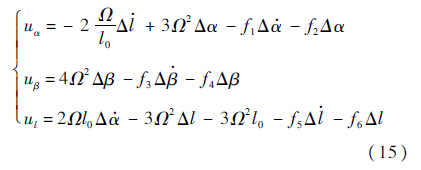
根据赫尔维茨稳定判据,二阶线性系统稳定充要条件为特征方程各项系数为正.将控制u代入式(14)整理,f1~f6>0时,就可保证系统式(14)严格稳定,从而原系统式(9)在零点附近局部渐进稳定.
同理可对切向编队保持(α0=90°,β0=0°,l=l0)模型线性化、稳定分析及设计控制律.
仿真算例1 设mA=mB=100kg,考虑电磁系统的可实现性,μB始终沿着zt方向,大小为105H/m,μA的各个轴分量μi(i=α,β,l)不超过4×104H/m,系统质心初始轨道根数见表 1.切向编队l0=25m,α0=π/2rad,β0=0 rad;径向编队l0=25m,α0=β0=0 rad.初始偏差均为:Δl=1m,Δα=-0.1rad,Δβ=0.1rad.
| 参数 | a/km | e | i/(°) | Ω/(°) | ω/(°) | θ/(°) |
| 取值 | 6878.1 | 0 | 0 | 0 | 0 | 0 |
仿真结果见图 2和图 3,仿真曲线表明当仿真时间较短、α和β偏差较小时,线性化模型能很好地代替非线性模型.利用设计的控制律,500s内将l,α,β误差控制到0,有良好的鲁棒性.
 |
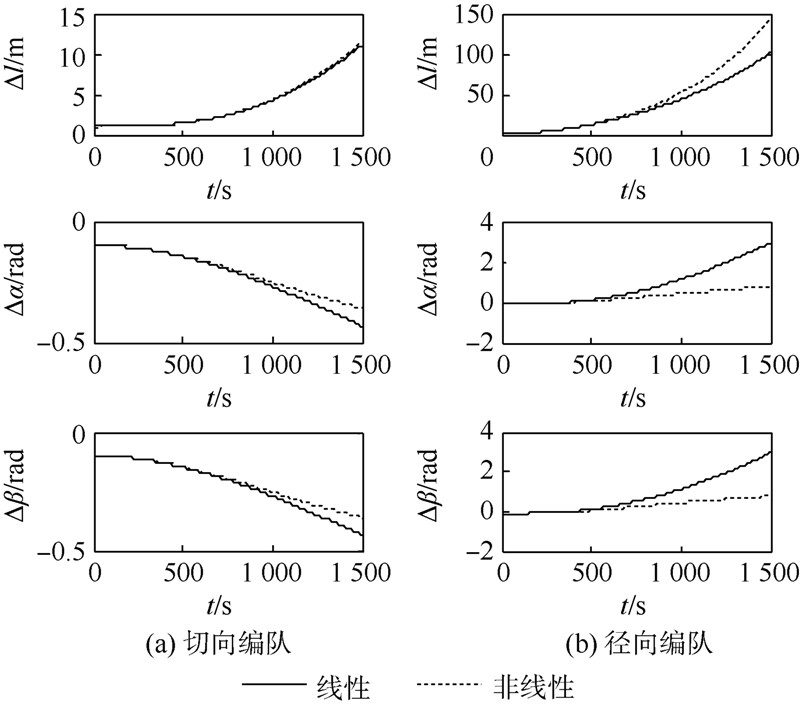| 图 2 电磁编队线性化与非线性动力学模型比较Fig. 2 Comparison between linear and nonlinear dynamics models for EMFF |
 |
| 图 3 电磁编队构型保持状态误差变化曲线Fig. 3 State parameter error variations of EMFF system |
电磁航天器编队重构问题,实际上可以转化为运动轨迹规划问题进行求解.
定义状态变量为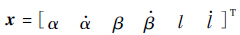
,控制磁矩为u=[μα μβ μl]T,则“绳系”动力学系统模型式(9)可整理为
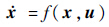;考虑电磁系统的可实现性及防碰撞,约束条件为μi≤μmax;l≥lmin,初始和终端约束条件为x(t0)=x0,x(tf)=xf.电磁航天器运动优化性能指标可以选为:
1) 时间性能指标.
2) 重构过程平缓的性能指标.
3) 系统能量性能指标.
电磁编队重构过程中,设μB保持不变,只需考虑A星电磁能消耗情况.带电线圈磁矩μ可表示为μ=NISn,其中N为线圈匝数,I为电流,S为线圈面积,n为载流平面法线方向单位向量,服从右手定则.带电线圈固装在电磁航天器本体上,磁矩μ在St系和本体系的投影存在如下关系：
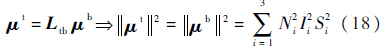
电功率为P=I2R,利用μt和μb计算出的电功率之和是相等的.所以系统能量性能指标可选为
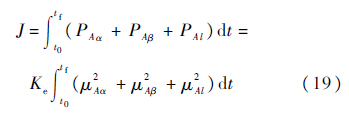
基于式(9),将双星电磁航天器编队运动规划问题转化成标准优化问题.高斯伪谱优化方法具有求解精度高和收敛速度快等优点[15],所以本文采用高斯伪谱方法对该优化控制问题进行求解,求得有限点处的控制近似解,再利用数值插值获得电磁航天器在重构过程中的控制磁矩u(t),具体算法及推导过程参见文献[15].
仿真算例2 假设mA=100kg和mB=200kg,l由25m重构变为15m,t0和tf时刻其他构型状态都为0.为了避免碰撞,限定l不小于10m.初始时刻AB编队系统质心轨道根数见表 1.高斯伪谱法优化指标采用电能消耗最优.
仿真结果如图 4和图 5所示,两星距离由25m平滑地变化到15m,速度不超过0.01m/s,α，β及其变化率满足tf时刻状态要求.由于采用能量最优为优化指标,各轴磁矩变化都比较平滑.
 |
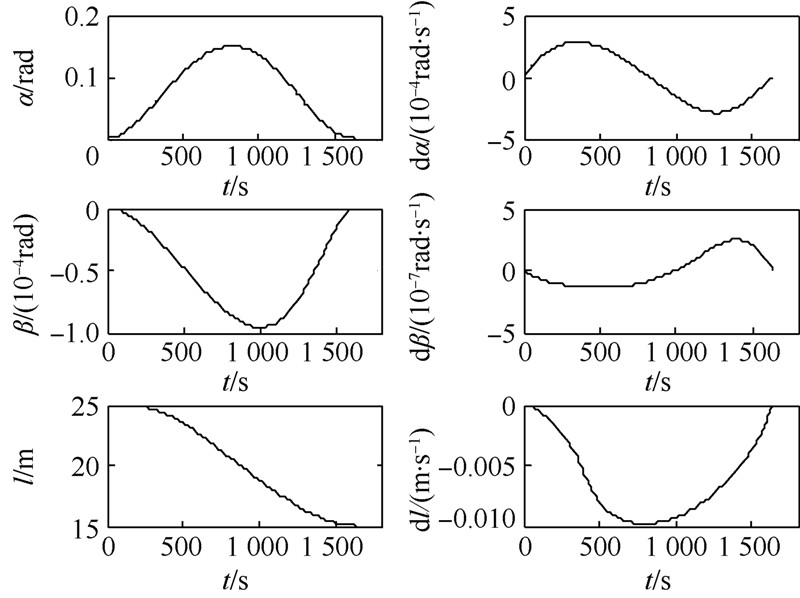| 图 4 双星电磁编队构型状态参数变化Fig. 4 State parameter variations of two-craft EMFF reconfiguration |
 |
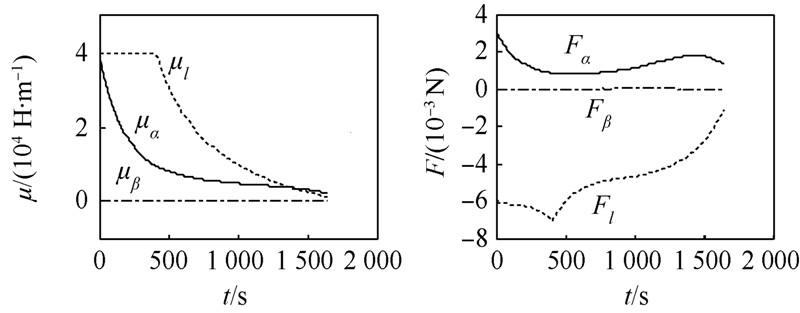| 图 5 电磁编队控制磁矩与电磁控制力Fig. 5 Electromagnetic control(magnetic dipole and force) of two-EMFF reconfiguration |
式(9)形式上只适用于双星电磁航天器编队,本文对是否可以利用式(9)完成复杂的多电磁航天器编队控制任务进行研究.提出序列控制策略,按照某个顺序,通过两两控制,逐一将各电磁航天器控制到目标状态.
设电磁航天器编队系统由N个航天器组成,其相对位置矢量和质量分别为ri和mi.由于电磁作用不改变编队系统质心位置,即
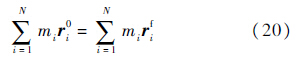
不失一般性,选择“1号”航天器通过电磁力作用,逐个将其余控制到目标位置:
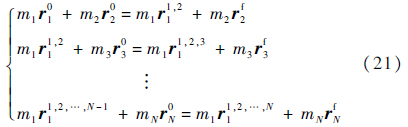
经过分析可得r1，2，…，N1=rf1,最终“1号”航天器自然能够到达其期望位置.“1号”航天器在重构过程中可自由选择.由此,序列控制的重点在于如何选择控制对、控制优先级和确定控制方案的标准.例如,可以把控制时间最短、最节省能量或其他特殊任务约束、环境条件、航天器状态等因素作为约束指标.另外,电磁航天器相对作用距离较短(100m以内),为了避免星间碰撞,重构过程必须考虑防碰撞策略.
例如图 6,三星电磁系统编队构型重构过程的序列控制次序选择为:[t0,tm],利用C将A控制到目标状态;[tm,tf ],利用C将B控制到目标状态.从而通过序列控制策略将多星电磁航天器编队运动规划问题转化为多阶段运动规划问题.基于Rao等[16]给出求解多段优化问题的GPOPS(Gauss Pseudospectral Optimization Software)算法,本文将多阶段运动规划转化为多阶段优化问题进行求解,算法推导详见文献[16].
 |
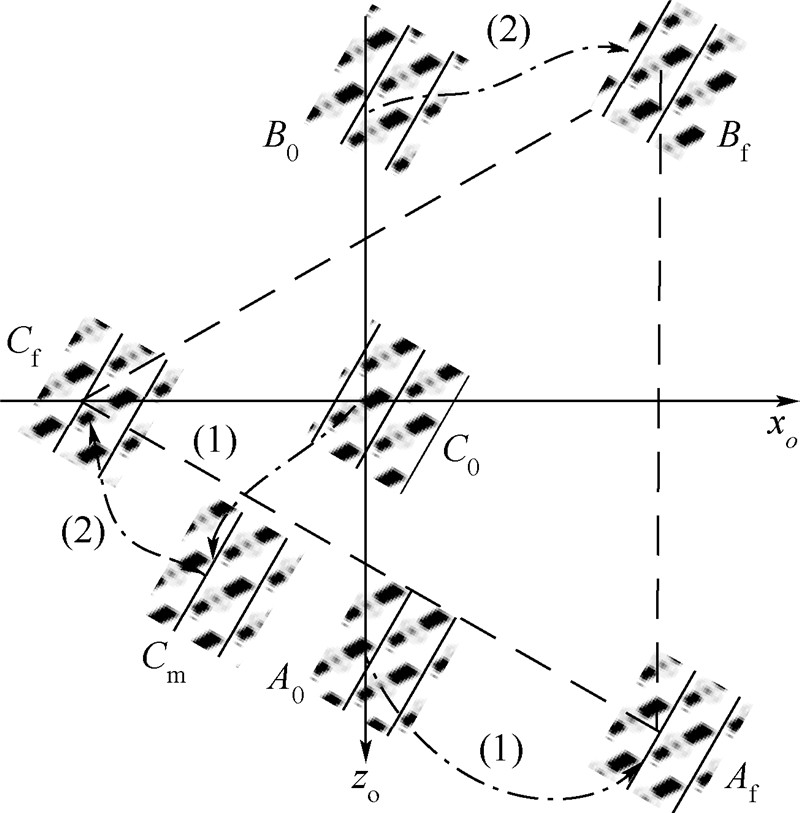| 图 6 构型重构序列控制示意图Fig. 6 Sequence control of multi-reconfiguration maneuver |
仿真算例3 考虑A,B,C三星系统,mA=mB=100kg,mC=200kg,轨道根数见表 1,重构过程如图 6所示;μC始终沿着相应的zt方向,恒为8×104H/m;μA和μB在St系各个轴磁矩μi(i=α,β,l)最大不超过4×104H/m.为了避免碰撞,限定A,B,C两两距离l要不少于10m.采用高斯伪谱法进行序列控制轨迹规划,选时间最优为优化指标.
仿真结果如图 7~图 9所示,编队重构过程分为两个阶段(仿真结果为t0=0s,tm=470s,tf=1568.5s):[t0,tm]段A,C相互作用,使A到达目标状态;[tm,tf ]段B,C相互作用,使A到达目标状态.控制磁矩几乎都达到了最大4×104H/m,呈现出Bang-Bang控制的特点,这与选时间最优为性能指标相吻合.
 |
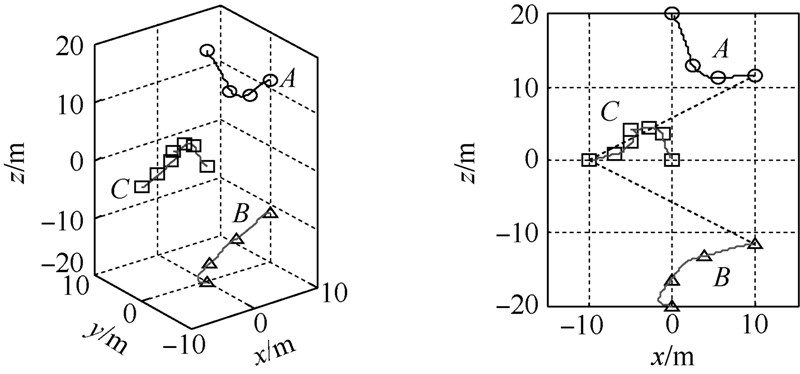| 图 7 电磁航天器构型重构优化路径示意图Fig. 7 Optimal trajectories of multi-EMFF reconfiguration |
 |
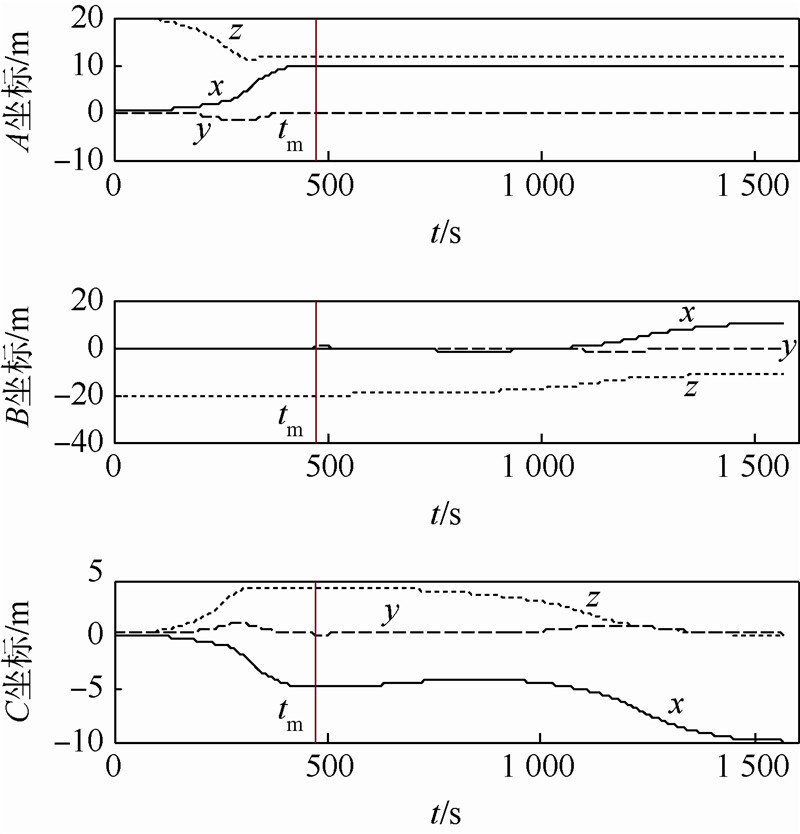| 图 8 A,B和C在重构变换过程中坐标变化Fig. 8 Position coordinates of multi-EMFF reconfiguration |
 |
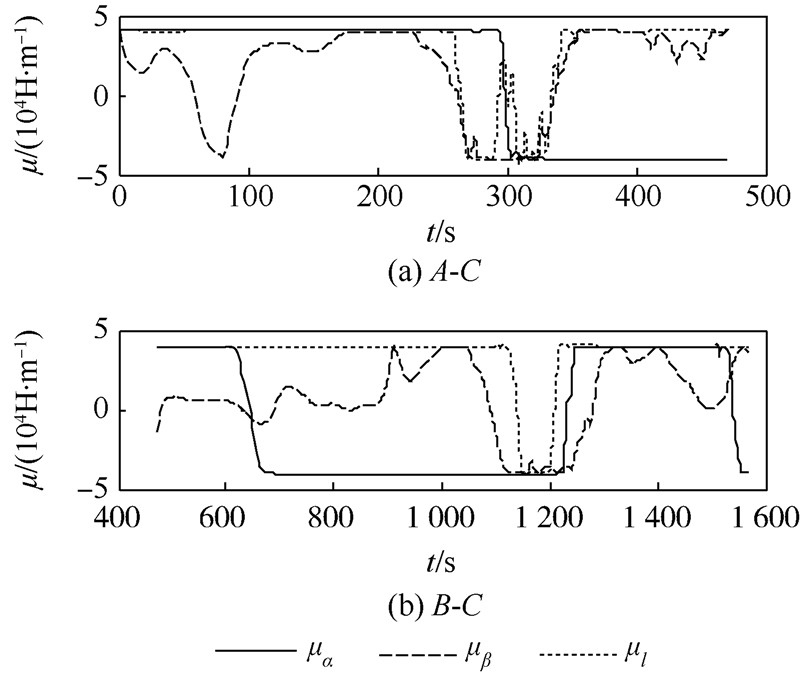| 图 9 A和B在重构变换过程中控制磁矩的变化Fig. 9 Histories of magnetic moments in reconfiguration |
本文建立了双星电磁航天器“绳系”动力学模型,利用线性化模型分析了电磁编队构型的稳定性,提出了序列控制策略,将多星电磁编队运动规划转化为多阶段优化问题.
1) 短时间、小偏差下,偏差线性化模型可以很好地代替原模型,可以简化模型的分析与控制;
2) 通过序列控制策略,利用双星模型可以有效地解决复杂高非线性多星电磁编队控制问题.
| [1] | 王龙,杨乐平, 许军校.电磁编队飞行与电磁交会对接关键技术及进展[J].装备指挥技术学院学报,2009,20(1):74-78. Wang L,Yang L P,Xu J X.The key technology and development of electromagnetic formation flight and electromagnetic rendezvous docking[J].Journal of the Academy of Equipment Command & Technology,2009,20(1):74-78(in Chinese). |
| Cited By in Cnki (8) | Click to display the text | |
| [2] | Miller D W, Sedwick R J,Eliaset L,et al.NIAC phase I final report:electromagnetic formation flight[J].Final Raport Massachusetts Institute of Technology,2002,121:163-179. |
| [3] | Kong E, Kwon D W,Schweighartet S A,et al.Electromagnetic formation flight for multisatellite arrays[J].Journal of Spacecraft and Rockets,2004,41(4):659-666. |
| Click to display the text | |
| [4] | Ahsun U. Dynamics and control of electromagnetic satellite formations[D].Massachusetts:Massachusetts Institute of Technology,2007. |
| Click to display the text | |
| [5] | Ahsun U, Miller D W,Ramirez L.Control of electromagnetic satellite formations in near-earth orbits[J].Journal of Guidance,Control,and Dynamics,2010,33(6):1883-1891. |
| Click to display the text | |
| [6] | 苏建敏,董云峰. 电磁卫星编队位置跟踪滑模变结构控制[J].宇航学报,2011,32(5):1093-1099. Su J M,Dong Y F.Sliding mode variable structure control for electromagnetic satellite formation station-tracking[J].Journal of Astronautics,2011,32(5):1093-1099(in Chinese). |
| Cited By in Cnki (7) | Click to display the text | |
| [7] | Cai W W, Yang L P,Zhu Y W,et al.Formation keeping control through inter-satellite electromagnetic force[J].Science China Technological Sciences,2013,56(5):1102-1111. |
| Click to display the text | |
| [8] | 黄涣,杨乐平, 朱彦伟,等.双星电磁编队的动力学平衡态稳定性与控制[J].国防科技大学学报,2013,35(3):12-17. Huang H,Yang L P,Zhu Y W,et al.Stability and control of dynamics equilibrium for two-spacecraft electromagnetic formation[J].Journal of National University of Defense Technology,2013,35(3):12-17(in Chinese). |
| Cited By in Cnki (1) | |
| [9] | Huang H, Zhu Y W,Yang L P,et al.Stability and shape analysis of relative equilibrium for three-spacecraft electro- magnetic formation[J].Acta Astronautica,2014,94(1):116-131. |
| Click to display the text | |
| [10] | 苏建敏,董云峰. 利用人工势函数法的卫星电磁编队控制[J].北京航空航天大学学报,2012,38(2):213-217. Su J M,Dong Y F.Artificial potential function method for satellite electromagnetic formation control[J].Journal of Beijing University of Aeronautics and Astronautics,2012,38(2):213-217(in Chinese). |
| Cited By in Cnki (2) | Click to display the text | |
| [11] | Inampudi R, Hanspeter S.Optimal reconfigurations of two-craft coulomb formation in circular orbits[J].Journal of Guidance,Control,and Dynamics,2012,35(6):1805-1815. |
| Click to display the text | |
| [12] | Inampudi R, Hanspeter S.Orbit radial dynamic analysis of two-craft Coulomb formation at libration points[J].Journal of Guidance,Control,and Dynamics,2014,37(2):682-691. |
| Click to display the text | |
| [13] | Alinger D J. System analysis and design for the resonant inductive near-field generation system(RINGS)[D].Maryland:University of Maryland College Park,2013. |
| Click to display the text | |
| [14] | Porter A K, Alinger D J,Sedwick R J,et al.Dual-purpose resonate actuators for electromagnetic formation flight and wireless power transfer[C]//AIAA Guidance,Navigation,and Control Conference.Reston:AIAA,2014:1-18. |
| [15] | Benson D. A Gauss pseudospectral transcription for optimal control[D].Massachusetts:Massachusetts Institute of Technology, 2005. |
| Click to display the text | |
| [16] | Rao A V, Benson D A,Darby C,et al.Algorithm 902:GPOPS,a MATLAB software for solving multiple-phase optimal control problems using the Gauss pseudospectral method[J].ACM Transactions on Mathematical Software,2010,37(2):22:1- 22:39. |
| Click to display the text |
