计算流体力学中广泛应用时间推进法求解Euler方程[1].时间推进方法可分为显式和隐式2类.著名的隐式方法有Beam-Warming隐式格式[2]、MacCormack隐式方法、近似因子分解方法AF及其改进的对角化近似因子分解方法AF-ADI[3, 4, 5, 6],另外还有Yoon和Jameson[7]提出的应用谱半径分裂的LU-SGS方法.隐式方法的优点是计算稳定性好、阻尼特性好,因此对时间步长的约束小(一些无条件稳定的隐式格式对时间步长没有约束),收敛所需的步数少,从而整体计算时间少,计算效率高.但是隐式方法每一时间推进步都要求解线性方程组,因而计算量和存储量都较大,方法复杂,程序较难实现.对于非定常问题,Jameson[8]提出了一种双时间步(dual time step)方法,在冻结的真实时刻点上引入类似牛顿迭代的虚拟时间迭代过程,通过这种内迭代过程来提高损失的时间精度.双时间迭代法应用广泛,是目前最受欢迎的非定常计算方法.
本文根据算子分解的思想,利用通量分裂方法和虚拟时间线化方法,构造了一种新的求解Euler方程的隐式时间推进方法,该方法在保有常规隐式方法优点的基础上,格式简单,易于编程,避免了每一时间推进步的方程组常规求解过程,因此计算量和储存量小.与LU-SGS方法相比,新方法的优势在于格式更加简单,收敛更快(注:这里所说的常规隐式指采用最原始方法构造的隐式格式,不包括LU-SGS等方法,本文新方法与LU-SGS是并列关系不是继承关系).
1 计算方法
考虑守恒形式的一维Euler方程初值问题:
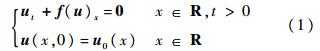
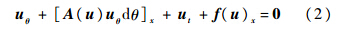
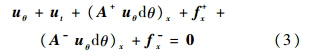
通量分裂形式为
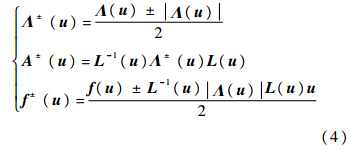
进一步,式(3)需要按算子分裂(或称算子分解)的思想,在时间上将此方程分解成几个方程,因为有2种时间,故此处有2种分裂方式.
1.1 按物理时间分裂
式(3)分解为
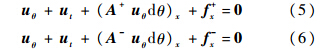
以式(5)为例推导格式,记Δukj=uk+1j－ukj,收敛时uk+1j=ukj=un+1j,上标k和n分别表示虚拟迭代次数和物理迭代次数,对式(5)做迎风离散,利用Crank-Nicolson方法,得
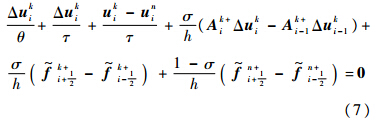
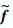为数值通量;下标i为节点序号;τ为物理时间步长;h为空间步长.整理后得到
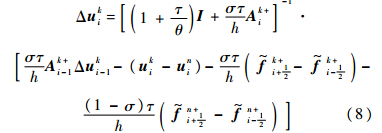
根据特征关系式(4),式(8)改写为
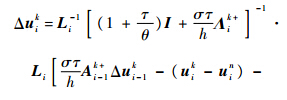
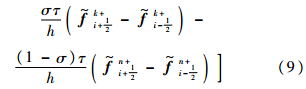
同理可得
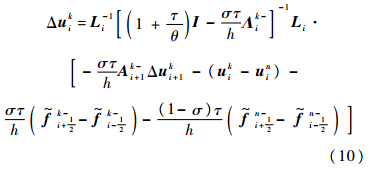
式(9)和式(10)为按物理时间分裂的最终差分格式求解公式.差分格式一个物理时间步的数值解的合成有如下2种方式:
1) 2个方向分别进行虚拟时间合成,然后再做一次物理时间合成:
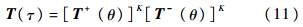
2) 2个方向混合进行虚拟时间合成:
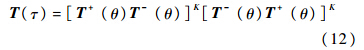
1.2 按虚拟时间分裂
式(3)分裂为
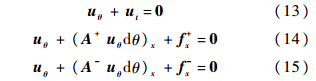
推导思路同1.1节,推导过程省略,得到按虚拟时间分裂的最终差分格式求解公式:
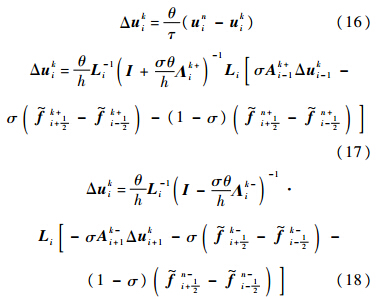
差分格式一个物理时间步的数值解的合成:
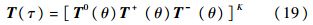
1.3 二阶时间精度 1.3.1 按虚拟时间分裂
方法1物理时间离散采用二阶形式,即
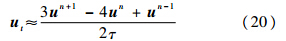
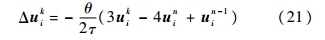
正通量方向和负通量方向的最终差分格式求解公式仍为式(17)、式(18),但取σ=1.这种方法为多步方法,需要2个时间层un、un－1的值,令un和un－1迭代初值都等于u0.
方法2 令式(17)、式(18)中的σ=0.5,即为二阶时间精度[10],实际计算中为保证稳定性,内迭代最后一步取σ=0.5,其余步数σ=1.
1.3.2 按物理时间分裂
物理时间分裂二阶时间精度的方法与虚拟时间分裂的方法相同,这里直接给出公式.
方法1
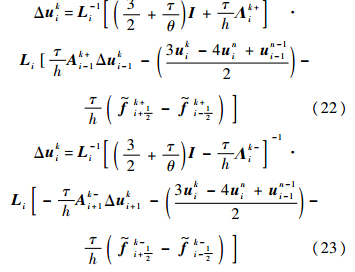
方法2式(9)、式(10)内迭代最后1步取σ=0.5,其余步数取σ=1.
1.4 数值通量选择
实际计算时,f~+i+12和f~－i－12可使用各种成熟格式的通量,主要使用NND格式和MUSCL格式.
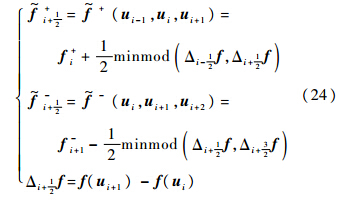
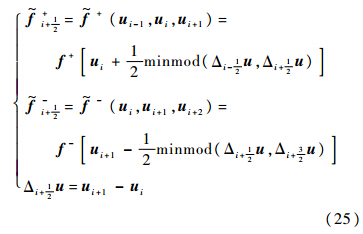
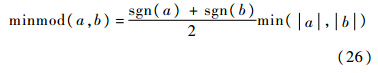
物理时间步长和虚拟时间步长选取方式为[8]
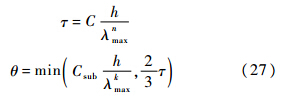
子迭代初值:uk=0=un.
子迭代收敛判据:残差定义同文献[15],为Δρkmax/θ,收敛条件为残差小于0.0001,子迭代步数限定为50.
1.5 定常问题隐式
虚拟时间隐式中,取消物理时间项,即式(16),则可以得到定常Euler方程的隐式方法,定常Euler方程的最终差分格式计算公式为式(17)、式(18),取σ=1.
1.6 其他问题
关于多维问题,一维问题算法可以通过维数分裂法直接推广到多维问题,因公式类似而不再重述.大量计算实践表明,在相同CFL数条件下(隐式虽然CFL数不受限制,但CFL数对解的品质有直接影响,进行效率对比必须在相同精度下进行),对于非均匀网格,分裂法比不分裂法计算速度要快,并且与不均匀度成正比.
关于收敛性或稳定性问题,这里沿用Lax等价性定理(线性格式的定理,本文的隐式部分属于局部线性格式,故此定理可做参考)的结论,稳定性与收敛性是一致的,所以这个词用任何一个都意味着另一个也成立(由于虚拟时间隐式是个迭代过程,所以使用收敛性这个词).注意,分裂隐式的线化矩阵选择并不唯一,根据隐式格式的绝对稳定性要求,当线化矩阵特征值的模大于原通量相应特征值模的一半以上时,隐式迭代过程收敛.而当线化矩阵的特征值等于原通量的相应特征值时,收敛最快.并且,当虚拟时间步长与物理时间步长取一致且通量为线性退化情形时,可一步收敛.
2 算例验证 2.1 Sod激波管
初始条件为
采用300个等距网格,C=1.0,Csub=2.0,数值通量使用NND格式,t=0.15s时密度分布计算结果如图 1所示.
 |
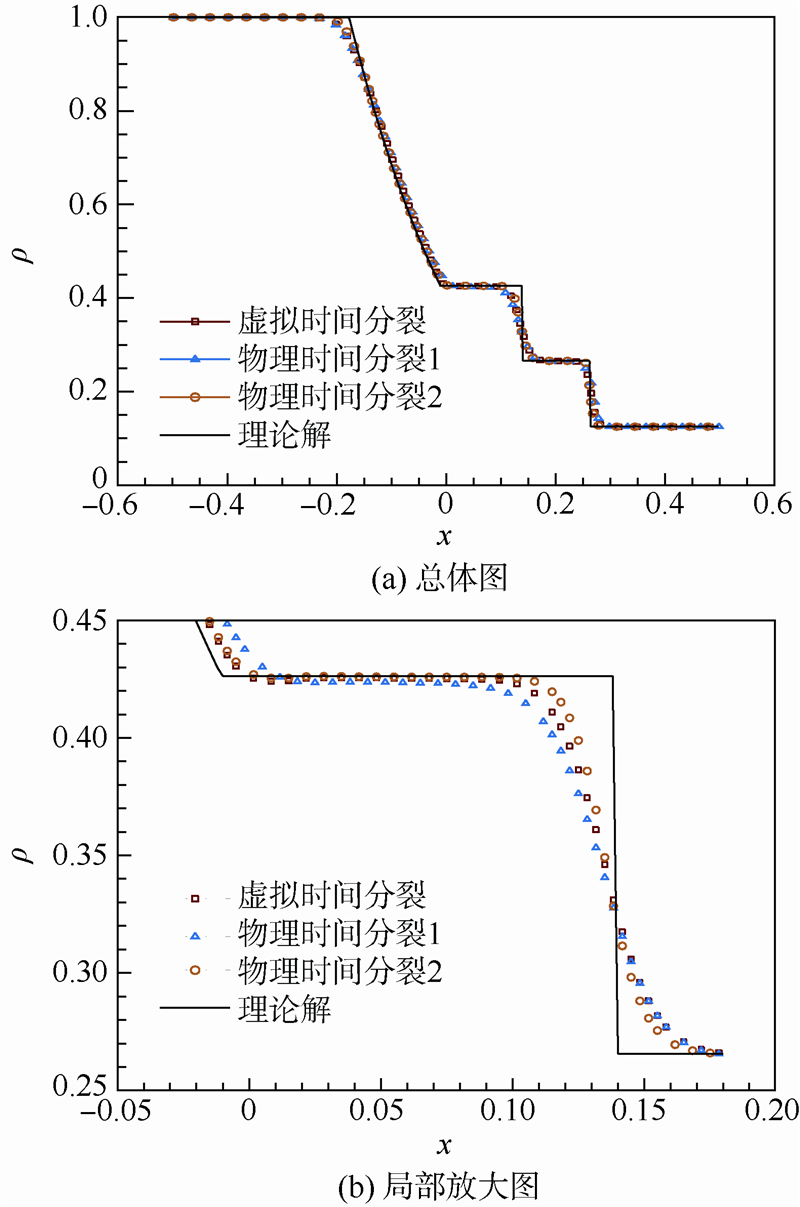| 图 1 t=0.15s时密度分布计算结果Fig. 1 Results of density distribution when t=0.15s |
由图 1可以看出,2种分裂方法都有较好的时间精度,其中物理时间分裂2格式的时间精度最高.
采用物理时间分裂2格式,二阶时间精度计算结果如图 2所示.
 |
| 图 2 二阶时间精度计算结果Fig. 2 Results of second order time accuracy |
图 2表明这些二阶时间精度的方法具有提高时间精度的效果.
2.2 Lax激波管
初始条件为
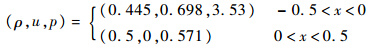
数值通量使用MUSCL格式,采用虚拟时间分裂格式.
对于均匀网格情况,要保证相同计算量,网格数N与CFL数可取如下关系：N=300C,C分别取1.0、4.0、9.0,计算结果如图 3所示.
 |
| 图 3 均匀网格情况、相同计算量下不同CFL数的 计算结果Fig. 3 Results with the same computations and different CFL numbers for uniform grid |
由图 3可看出,在相同计算量情况下,CFL数对计算结果影响不大,说明本文方法在大CFL数下也能保证一定的精度要求.
2.3 改进的Lax激波管
初始条件为
该算例是Lax激波管的修改,接触间断位置固定.此算例可考察隐式方法对定场流场的计算效果,因为接触间断位置固定,可以排除时间精度对解的影响.实际问题多采用非均匀网格,局部网格加密而时间步长不变等价于增大CFL数,为保证同等计算量,网格数与CFL数取如下关系:N=100C,C分别取1.0、6.0,数值通量使用MUSCL格式,采用虚拟时间分裂格式,计算结果如图 4所示.
 |
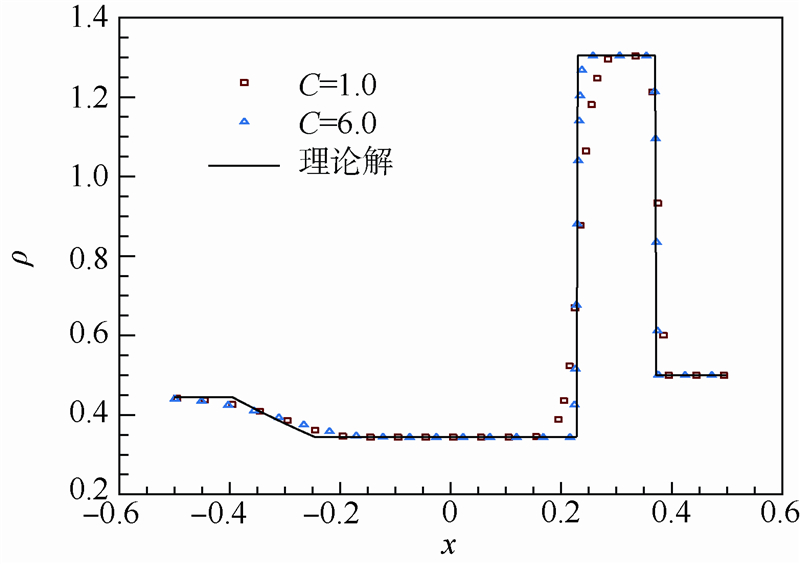| 图 4 非均匀网格情况、相同计算量下,不同CFL数的 计算结果Fig. 4 Results with the same computations and different CFL numbers for non-uniform grid |
由图 4可看出,当考虑非均匀网格情况时,在相同计算量下,增加CFL数可以提高计算精度,表明本文方法对于实际问题更有价值.
2.4 超声速流绕前台阶流动
流动初始参数ρ1=1.0,u1=3.0,流动速度v1=0,p1=0.71429,计算模型示意图如图 5所示.
 |
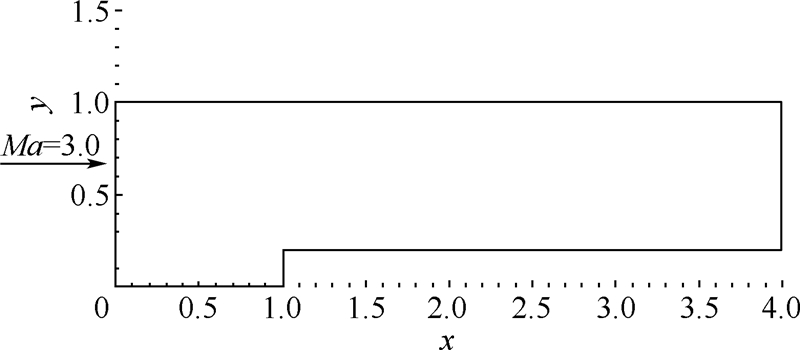| 图 5 计算模型示意图Fig. 5 Schematic diagram of calculation model |
初始条件:当t=0时,全流场内充满了马赫数为3.0的超声速气流.
边界条件:左边界(x=0,0≤y≤1.0)处为马赫数为3.0的均匀来流.右边界(x=4,0.2≤y≤1.0)为自由输出条件.上边界、下边界和前台阶物面均为刚性边界,满足滑移反射边界条件.
这是一个非定常问题,采用虚拟时间分裂格式,为比较相同计算量下不同CFL数对计算结果的影响,故采用两套网格进行计算.
2.4.1 计算条件1
采用50×10和200×40两块网格,C=1.0.前台阶网格1如图 6所示.
 |
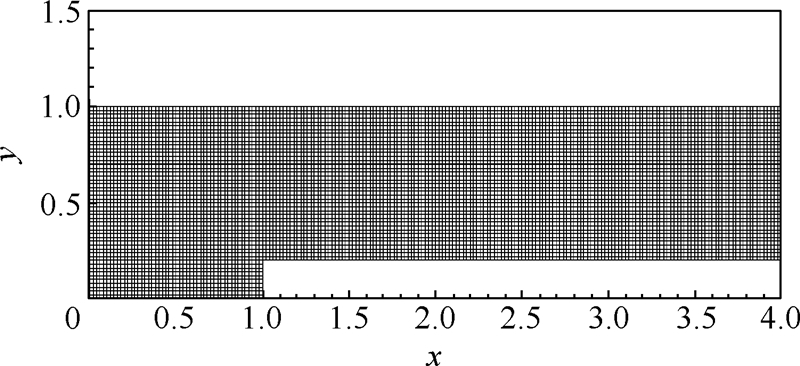| 图 6 前台阶网格1Fig. 6 Grid 1 of forward-facing step |
网格1前台阶绕流等密度线分布(C=1.0)随时间变化情况如图 7所示.
 |
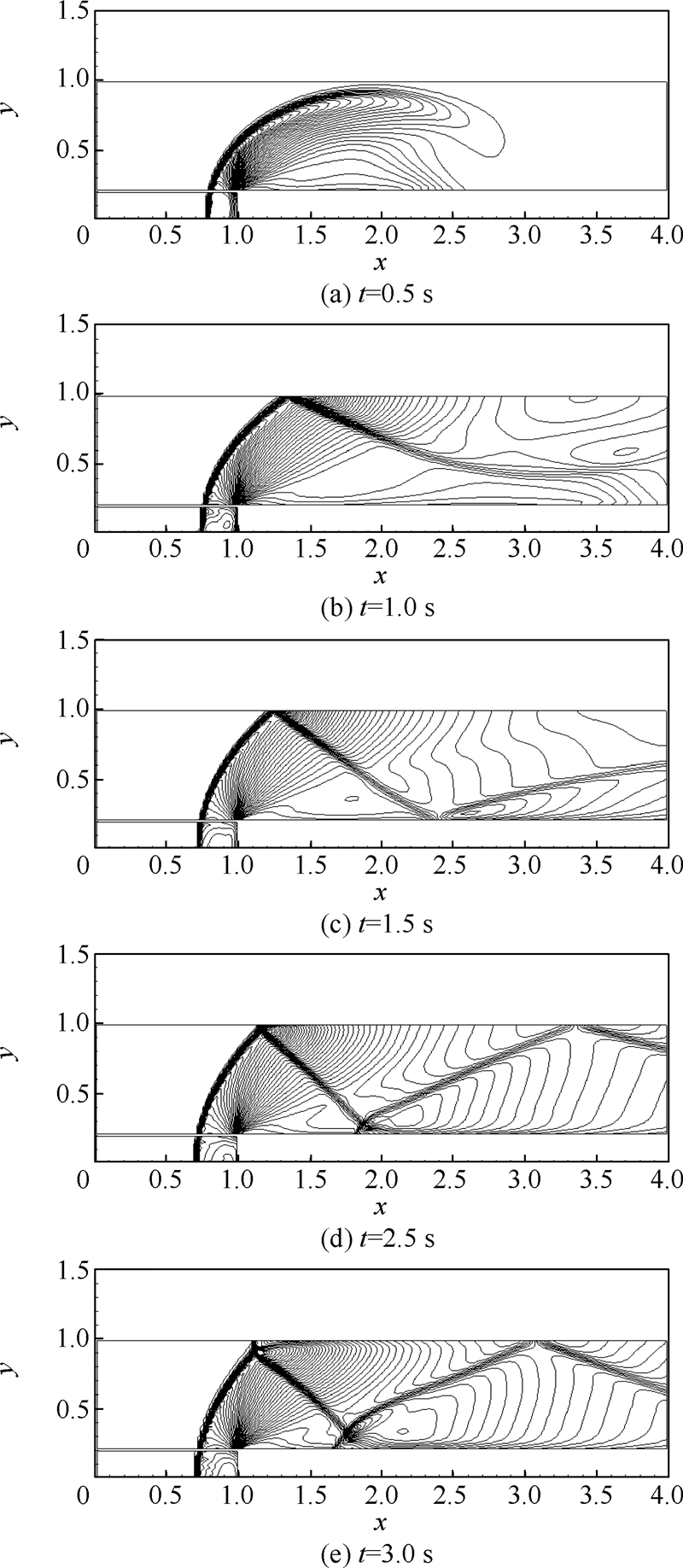| 图 7 网格1前台阶绕流等密度线分布(C=1.0)Fig. 7 Density contours of forward-facing step flow for Grid 1 (C=1.0) |
2.4.2 计算条件2
采用100×20和400×80两块网格,C=8.0.前台阶网格2如图 8所示.
 |
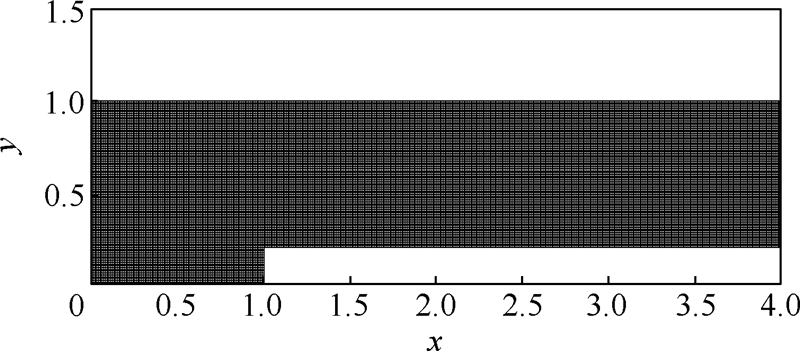| 图 8 前台阶网格2Fig. 8 Grid 2 of forward-facing step |
网格2前台阶绕流等密度线分布(C=8.0)随时间变化情况如图 9所示.
 |
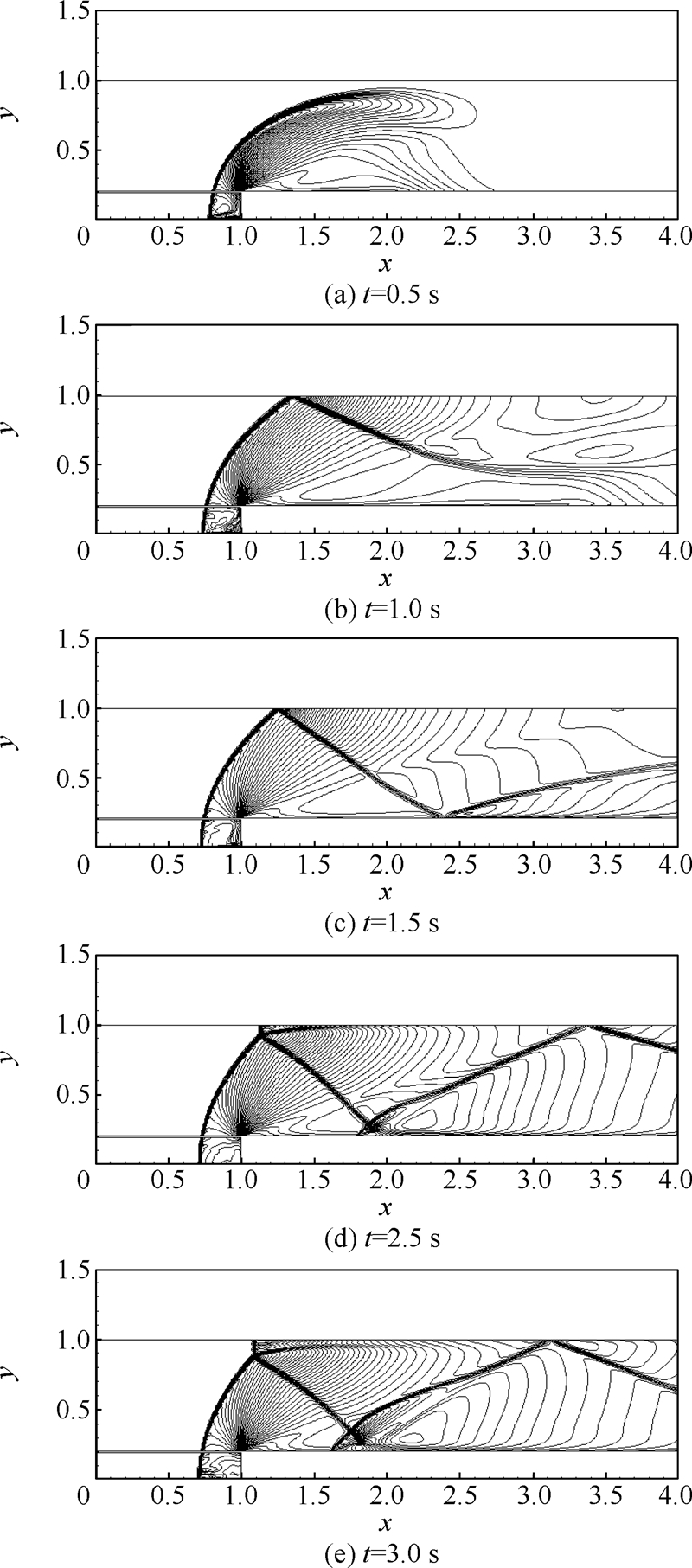| 图 9 网格2前台阶绕流等密度线分布(C=8.0)Fig. 9 Density contours of forward-facing step flow for Grid 2 (C=8.0) |
以上计算可得到与2.2节相同的结论.
2.5 NACA0012翼型绕流
NACA0012翼型网格如图 10所示,网格数为239×59.
 |
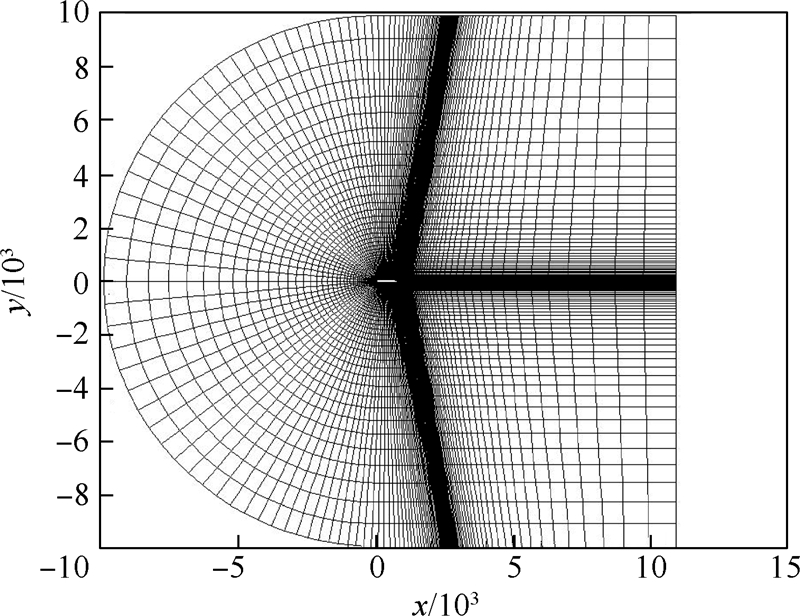| 图 10 NACA0012翼型网格Fig. 10 Grid of NACA0012 airfoil |
1) 来流马赫数为0.8,攻角为1.25°.
在来流马赫数为0.8,攻角α为1.25°来流条件下,绕翼型的流场属超临界状态,在翼面上将形成附体激波.上翼面激波较强,下翼面会形成一道很弱的激波.
流场压强等值线和翼型表面压强系数Cp分布如图 11(a)~图 11(d)所示.
 |
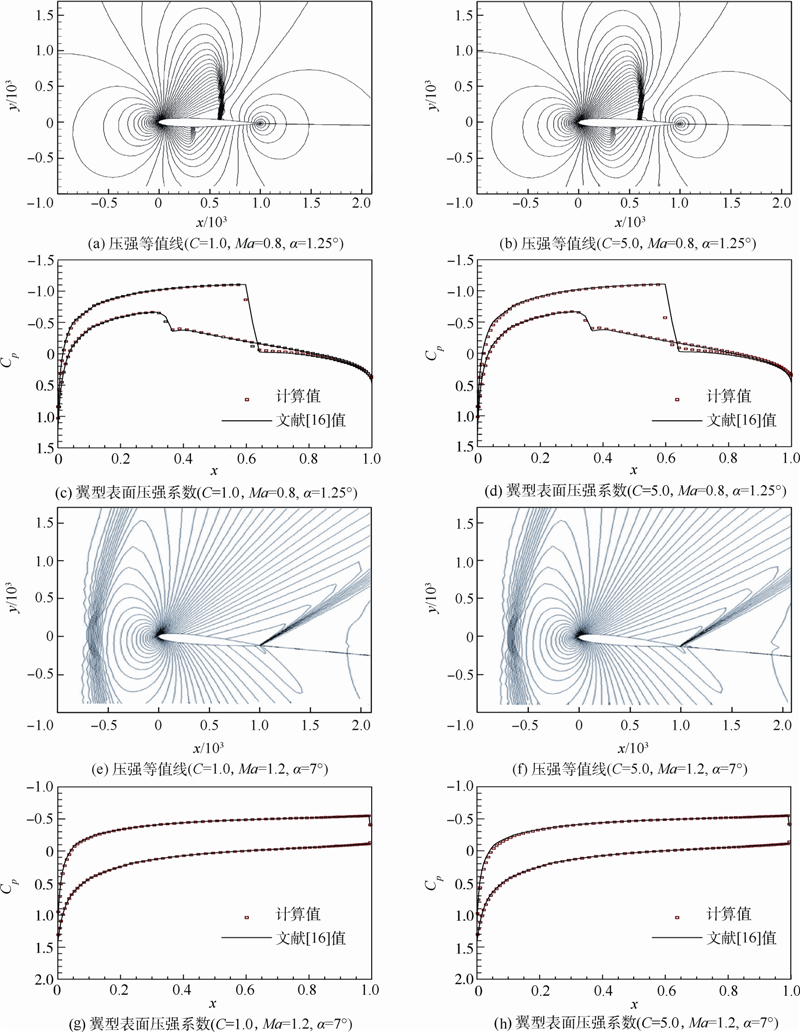| 图 11 流场压强等值线和翼型表面压强系数分布Fig. 11 Pressure contours and pressure coefficients on airfoil surface |
计算结果表明,在不同的CFL数下,本文方法均能捕捉到翼型上表面的强激波和下表面的弱激波,且与文献[16]吻合度良好.
2) 来流马赫数为1.2,攻角为7°.
在来流马赫数为1.2,攻角为7°来流条件下,其绕流场将在翼型头部形成脱体的弓形激波,在后缘形成鱼尾激波.
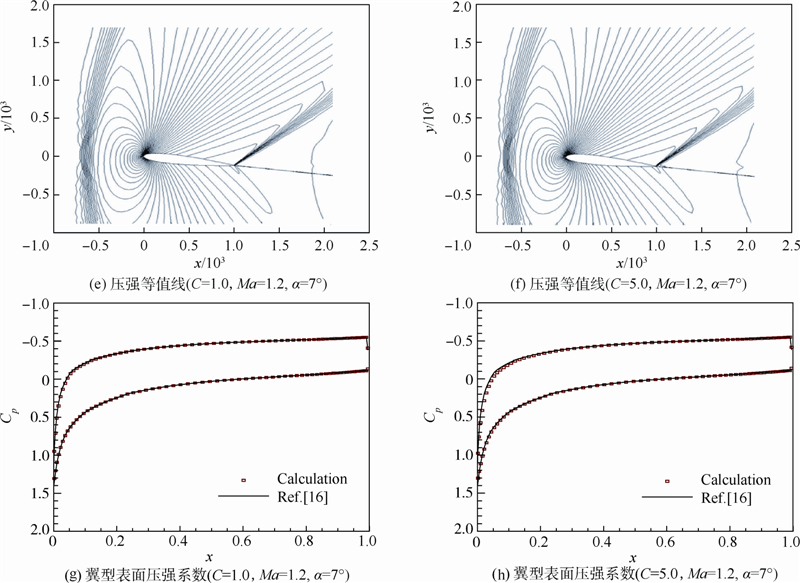
流场压强等值线和翼型表面压强系数分布如图 11(e)~图 11(h)所示.
计算结果表明,在不同的CFL数下,本文方法均能捕捉到头部的弓形激波和后缘的鱼尾激波,且与文献[16]吻合度良好.
2.6 双椭球无粘绕流
计算网格如图 12所示,网格数为51×39×19.
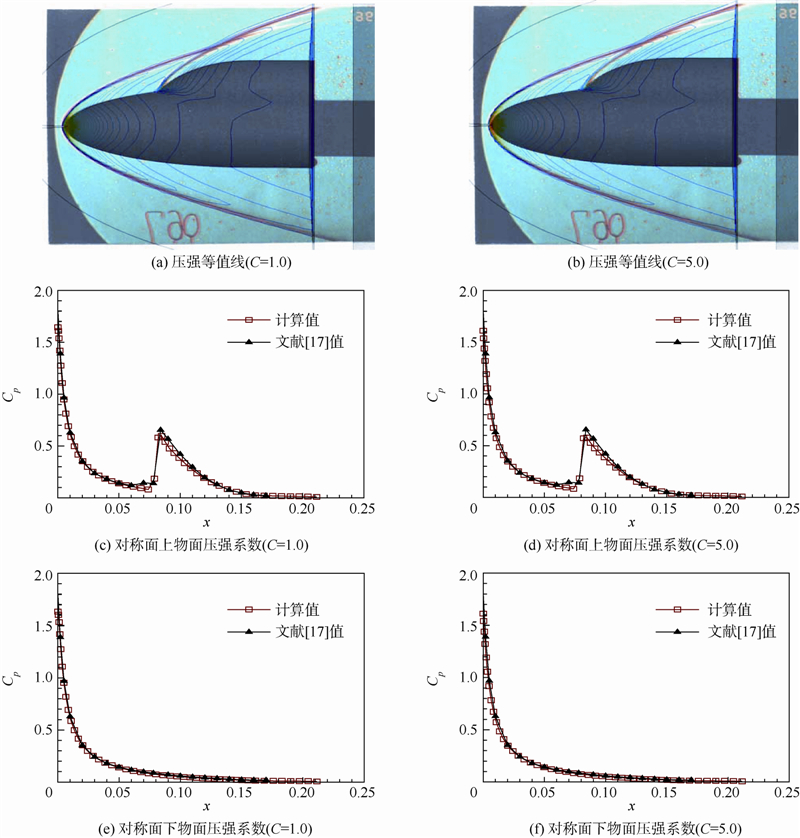
计算条件:来流马赫数Ma=8.0,攻角α=0°,侧滑角β=0°.实验激波纹理照片如图 13所示[17].
 |
| 图 12 计算网格Fig. 12 Grid for calculation |
实验表明:在此马赫数下,椭球头部会形成脱体弓形激波,两椭球镶嵌处附近会出现二次激波.
流场压强等值线和对称面上下物面压强系数如图 14所示.
 |
| 图 14 流场压强等值线和对称面上下物面压强系数Fig. 14 Pressure contours and pressure coefficients on top and low surfaces |
计算结果表明,在不同的CFL数下,本文方法均可捕捉到两道激波,且和实验吻合良好.
通过2.5节和2.6节算例可以得出以下结论:本文方法可以增大CFL数，提高计算效率,并能够保持精度. 3 与LU-SGS方法的比较 3.1 Sod激波管
计算条件与2.1节相同,由于计算结果相近,故不再给出,图 15为Sod激波管2种方法的比较.
图 15说明了2个问题:①使用高阶时间精度的方法可以提高内迭代次数,从而提高计算效率.②在相同时间精度的情况下,本文方法物理时间推进一步所需的虚拟时间迭代次数少于LU-SGS方法的,即收敛速度更快.
 |
| 图 15 Sod激波管2种方法的比较Fig. 15 Comparison of two schemes in Sod shock tube |
计算条件同2.4节,图 16为前台阶绕流2种方法的比较.
 |
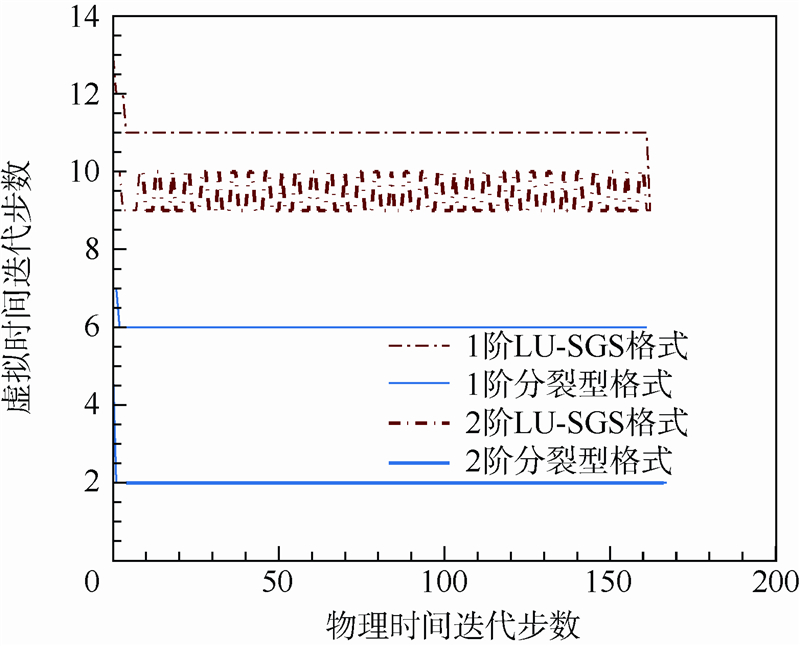| 图 16 前台阶绕流2种方法的比较Fig. 16 Comparison of two schemes in forward-facing step flow |
图 16的结果同样说明本文方法在收敛速度上更有优势.
LU-SGS方法为了提高计算效率,避免矩阵求逆,采用了简化的A±、B±、C±分解求法,故对求解的收敛性有了一定的影响,本文方法使用了严格的A±、B±、C±分解,所以收敛性能较好,也起到了减小计算量的作用.
发展了一种新的分裂型隐式方法,并利用典型的空气动力学问题测试其性能,可以得到以下结论:
1) 方法具有隐式格式的普遍优点,即稳定性好,CFL数可以放大;此外,方法格式简单,易于编程,单步时间推进不涉及方程组常规求解和矩阵求逆,计算量小,与LU-SGS方法相比,收敛更快.
2) 对于定常问题,方法可以在增大CFL数、提高计算效率的情况下保证精度.
3) 对于非定常问题,方法的计算精度主要由计算量决定,同等计算量下,不会随CFL数的增大而丧失精度.
| [1] | Pulliam T H. Development of implicit method in CFD NASA Ames Research Center 1970s-1980s[J].Computers & Fluids,2011,41(1):65-71. |
| Click to display the text | |
| [2] | Beam R M,Warming R F.An implicit finite-difference algorithm for hyperbolic system in conservation law form[J].Journal of Computational Physics,1976,22(1):87-109. |
| Click to display the text | |
| [3] | Beam R W,Warming R F.An implicit factored scheme for the compressible Navier-Stokes equations[J].AIAA Journal,1978,16(4):393-402. |
| Click to display the text | |
| [4] | Biringer M,McMillan O J.Calculation of two dimensional inlet fields by an implicit method including viscous effect:program documentation and test case,NASA-CR-81-3414[R].Washington,D.C.:NASA,1981. |
| [5] | Pulliam T H,Chaussee D S.A diagonal form of an implicit approximate factorization algorithm[J].Journal of Computational Physics,1981,39(2):347-363. |
| Click to display the text | |
| [6] | Chaussee D S,Pulliam T H.Two dimensional inlet simulation using a diagonal implicit algorithm[J].AIAA Journal,1981,19(2): 153-159. |
| Click to display the text | |
| [7] | Yoon S,Jameson A.Lower-upper symmetric Gauss-Sediel method for the Euler and Navier-Stoker equations[J].AIAA Journal,1988,26(9):1025-1026. |
| Click to display the text | |
| [8] | Jameson A. Time dependent calculations using multigrid with application to unsteady flows past airfoils and wings[C]//AIAA 10th Computational Fluid Dynamics Conference.Reston:AIAA,1991:1-4. |
| Click to display the text | |
| [9] | Steger J L,Warming R F.Flux vector splitting of the inviscid gasdynamic equations with application to finite-difference methods[J].Journal of Computational Physics,1981,40(2):263-293. |
| Click to display the text | |
| [10] | 张小蜂,张红武.Crank-Nicolson格式精度的改进[J].水科学进展,2001,12(1):33-38. Zhang X F,Zhang H W.Efficient improvement of Crank-Nicolson scheme[J].Advances in Water Science,2001,12(1):33-38(in Chinese). |
| Cited By in Cnki (20) | |
| [11] | 陈培基,陆夕云,庄礼贤.一种修正的隐式NND格式[J].计算物理,1996,13(3):379-384. Chen P J,Lu X Y,Zhuang L X.A modified implicit NND difference scheme[J].Chinese Journal of Computational Physics,1996,13(3):379-384(in Chinese). |
| Cited By in Cnki | |
| [12] | 张德良. 计算流体力学教程[M].北京:高等教育出版社,2010:331-332. Zhang D L.A course in computational fluid dynamics[M].Beijing:High Education Press,2010:331-332(in Chinese). |
| [13] | Collela P. A direct Eulerian MUSCL scheme for gas dynamics[J].SIAM Journal on Scientific and Statistical Compuing,1985,6(1):104-117. |
| Click to display the text | |
| [14] | 水鸿寿. 一维流体力学差分方法[M].北京:国防工业出版社,1998:509-512. Shui H S.Difference methods of one-dimensional fluid dynamics[M].Beijing:Defense Industry Press,1998:509-512(in Chinese). |
| [15] | 赵慧勇,乐嘉陵. 双时间步方法的应用分析[J].计算物理,2008,25(3):253-258. Zhao H Y,Le J L.Application analysis on dual-time stepping[J].Chinese Journal of Computational Physics,2008,25(3):253-258(in Chinese). |
| Cited By in Cnki (5) | |
| [16] | 钱战森. 大时间步长、高分辨率差分格式研究及其应用[D].北京:北京航空航天大学,2011. Qian Z S.On large time step,high resolution finite difference schemes for hyperbolic conservation laws and applications[D].Beijing:Beijing University of Aeronautics and Astronautics,2011(in Chinese). |
| [17] | 李素循. 典型外形高超声速流动特性[M].北京:国防工业出版社,2006:18-39. Li S X.Hypersonic flow characteristics of typical shapes[M].Beijing:National Defense Industry Press,2006:18-39(in Chinese). |
