2. 密歇根大学 机械工程系, 安娜堡 48109
2. Department of Mechanical Engineering, University of Michigan, Ann Arbor 48109, USA
多交点装配是一种典型的飞机结构连接形式,具有很高的装配协调准确度要求.为了获得良好的制造经济性,交点部件通常采用实物协调的方法制造,制造过程包含了较多的尺寸协调环节.由于装配准确度由工艺装备及零部件的多对交点尺寸公差共同决定,且与交点几何布局和交点协调类型相关,飞机多交点装配的公差设计难度大.工艺人员通常参照设计规范、依赖经验类比或手工计算进行公差设计,其试凑式的公差设计方法常常导致公差设计不合理、加工难度和成本增加以及装配协调突出等问题.本文研究飞机多交点装配的公差优化技术,旨在结合生产成本和制造知识来生成优化的公差控制信息,提高公差设计的可靠性和经济性.
公差由一系列离散的基本偏差和精度等级来表示,因此公差设计可视为设备、夹具及工具等工艺条件约束下若干离散公差值的优化选择问题.Moy[1]、Smathers和Ostwald[2]采用动态规划方法优选离散公差,将N个组件的离散公差分为N个优化子问题,然后根据Bellman定理来求解.Lee和Woo[3]把各环节公差精度等级定义为选择集内的一系列离散值,引入线性化的可靠性指数来表征装配的可靠性概率,进而建立了离散公差的整数规划模型;整数规划问题是一个NP困难问题,不存在一般意义上的通用解法,基于二叉树的穷举搜索法的复杂度为O(2n);提出了分枝估界算法,利用可靠性指数、成本与公差的单调关系以及启发式的初始解搜索方法来提高枚举树的遍历速度;其主要局限性是对树节点的成本和装配误差定界时,子节点对应的公差成本需重复计算,且树节点规模与公差变量维数呈指数关系,当公差设计环节较多时,算法效率严重降低.Chase等[4]针对尺寸公差环节存在多种制造工艺选择的情况,提出了基于单变量搜索和拉格朗日乘子法的离散公差优化方法,其主要不足在于公差成本曲线不连续时无法保证全局最优解.Kusiak和Feng[5]研究了整数规划法和实验设计法在离散公差优化中的应用,指出实验设计法能处理非线性成本函数和概率约束情况;但该算法仍属于穷举搜索的范畴,在求解大规模公差优化问题时同样存在效率低下的问题.Deng J和Deng S[6]提出了基于适应性分枝估界的离散公差优化方法,采用霍夫变换“由粗到精”逐步逼近策略进行公差区间划分,同时设置最大迭代次数来控制遍历规模;但该方法以局部搜索策略来提升效率,无法保证解的全局最优.Kumar等[7]提出了基于禁忌搜索和启发式规则的离散公差优化方法,但没有论证公差解的全局最优性.Xue和Ji[8]应用遗传算法求解离散公差问题,并将其应用于二维角度公差图问题.Lf等[9]采用拉格朗日法和对偶单纯形法求解离散公差优化的整数规划问题,通过公差选择系数的分枝和目标函数的定界改善了算法效率.Lf和Sderberg[10]又将上述方法推广到产品族组件的离散公差优化设计.Sivakumar等[11]研究了多种工艺选择下的公差优化方法,采用改进遗传算法和多目标粒子群算法实现了工艺和公差的优化选择.Geetha等[12]研究了面向制造成本、质量损失和加工闲置时间的多目标公差优化,采用遗传算法实现了工艺及机床选择的离散公差优化.
总的来说,上述研究主要针对一般机械产品的结构尺寸公差优化问题,各环节的公差可作为独立变量进行优化.飞机多交点装配的公差优化具有其特殊性.首先,公差设计针对装配交点处孔、轴公差配合的优化选择,需将孔、轴配合的公差带宽和基本偏差作为统一的设计变量纳入装配约束条件和公差优化模型中.各环节公差不再是独立的设计变量,相邻尺寸环节间的公差选择具有关联性.其次,公差成本函数中公差带宽为自变量,而受装配功能约束方程则与作为设计变量的公差带宽及基本偏差相关,公差与成本、装配性能间不存在严格的单调关系,因此分枝估界算法[3, 6]不适用于多交点装配公差优化.此外,多交点装配协调误差与设计公差存在复杂的非线性关系,也不适合基于拉格朗日乘子法的线性规划方法求解.
飞机多交点装配公差设计是一个多阶段决策过程,本文采用动态规划方法建立其离散公差优化模型.公差优化由基于动态规划有向图模型的“回溯”和“前溯”两个阶段来实现.首先,在“回溯”阶段逆序求解有向图各状态节点后部子过程的最优成本指标和装配性能指标,作为有向图节点的二元属性值;然后,在“前溯”阶段根据各状态节点的成本和装配性能指标,对最优路径进行启发式搜索,实现最优公差值策略的高效搜索.该方法可避免公差优化中成本和装配性能的重复计算,提高了最优解的寻优效率,能够保证公差的全局最优性.
1 多交点装配功能的数学描述
公差设计须保证多交点部件交点孔、轴处的累积装配(或协调)误差小于装配工艺要求的同轴度误差.飞机多交点装配有两种主要形式:一种是机身、机翼类固定部件装配的平面交点结构,即4对(或4对以上)交点接头对合于理论平面(或主要交点位于理论平面上),称之为4交点装配,其装配协调要求主要体现为对合部件的交点共面度误差约束;另一种是舱门和门框类活动部件装配中的直线交点结构,即3对(或3对以上)交点接头对合于理论轴线上,称之为3交点装配,其装配协调要求主要体现为交点的直线度误差约束.在实物协调方式下,各制造单元(标工、装配夹具和产品部件)的交点位置通过孔-轴-孔配合进行“移制”.由于随机变化的孔、轴配合间隙,交点“移制”过程将不可避免地引入误差并最终累积到交点部件上,使各交点位置偏离理论装配平面或装配轴线.
不失一般地,设交点部件PM和PN具有图 1所示的制造协调路线.其中,标工P0是原始协调依据,部件PM的交点依次经工装P1、P2、…、PM-1“移形”制造,部件PN的交点由工装PM+1、PM+2、…、PN-1“移形”制造,称相邻制造单元的尺寸形状传递为移形环节.例如,移形环节“P0→P1”表示由标工的P0交点移制工装P1的交点,具有交点装配协调要求的部件PM和部件PN协调环节用“PMPN”表示.Δi和∇i(i=1,2,…,N)分别表示制造单元和移形环节的误差.若∇N+1表示协调环节的交点装配误差,则由于误差累积导致的交点部件协调误差为
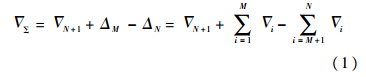
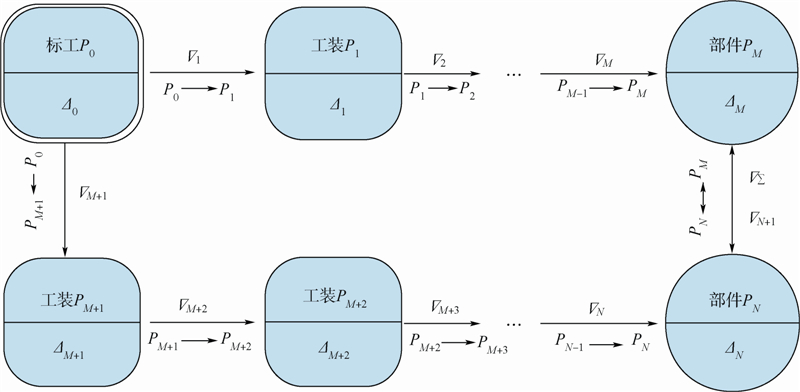 |
| 图 1 多交点部件制造协调过程Fig. 1 Manufacturing and coordination process of multi-joint parts |
程宝蕖[13]给出了3交点装配和4交点装配准确度表达式.图 2为3交点装配部件PM和PN的协调误差示意图.设l1和l2分别表示交点1与交点2、交点3的欧氏距离,根据误差传播过程和几何关系,可得

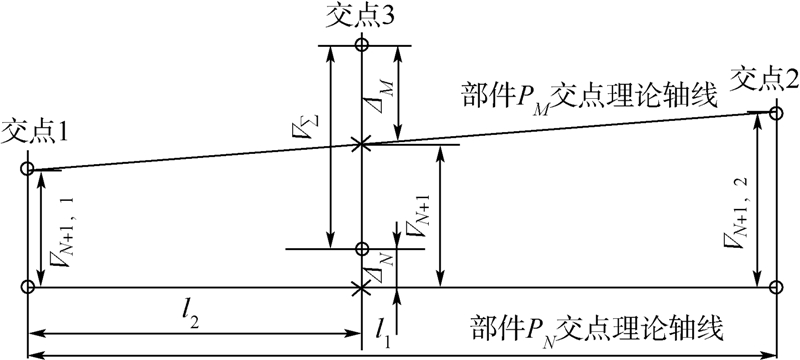 |
| 图 2 3交点装配的协调误差Fig. 2 Coordination error of three-joint assembly |
图 3为4交点装配部件PM和PN的协调误差示意图.各环节的协调误差为
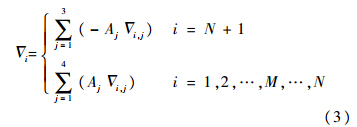
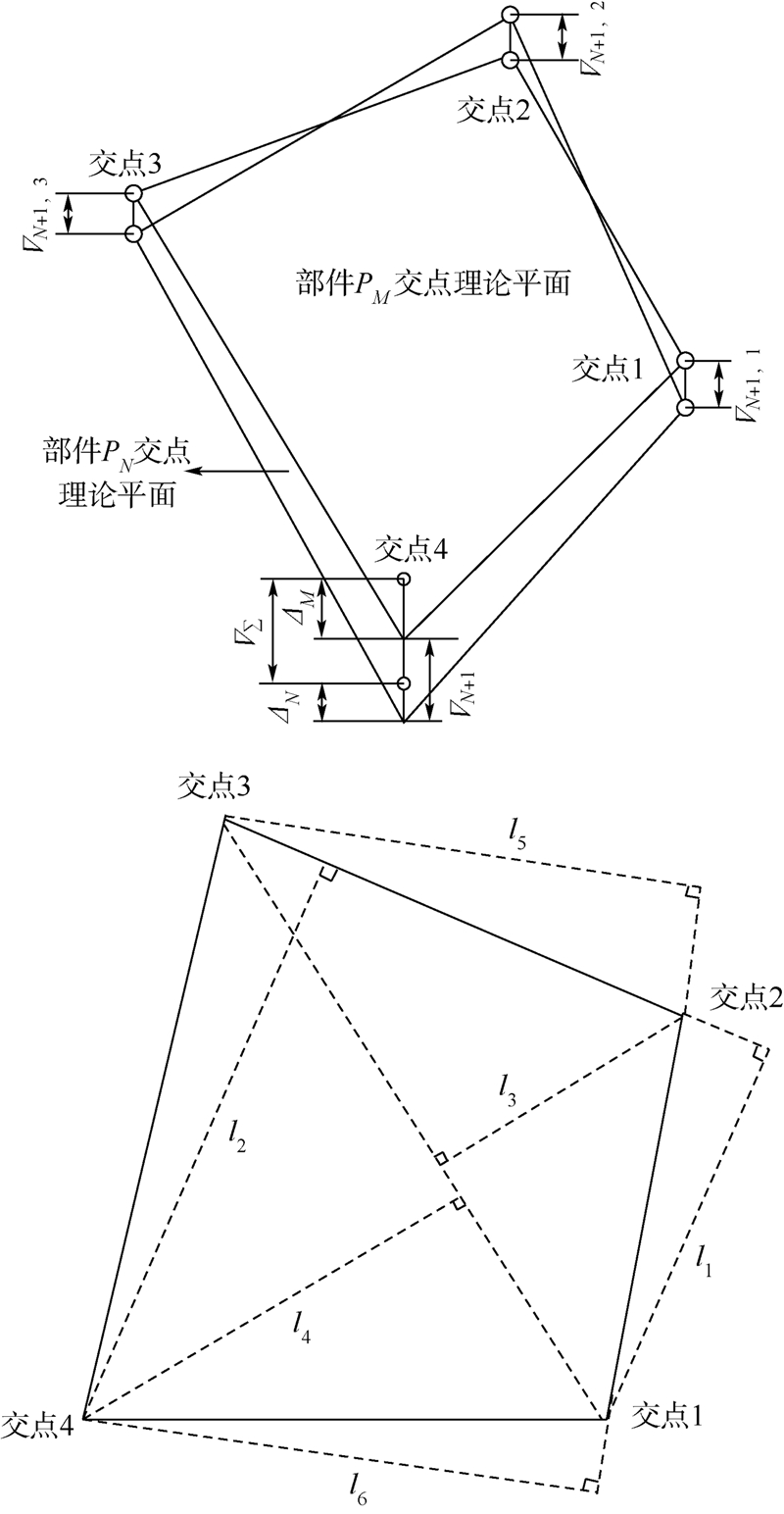 |
| 图 3 4交点装配的协调误差Fig. 3 Coodination error of four-joint assembly |
通过式(1)计算误差累积导致的交点部件协调误差时,需先计算各交点在孔、轴配合约束下的移形误差大小.第i个移形或协调环节第j对交点的孔-轴-孔配合可用六元组Γi,j=(Ti,ja,Ti,jb,Ti,jc,(δi,ja)0,(δi,jb)0,(δi,jc)0)表示,其中Ti,ja、Ti,jb和Ti,jc分别为状态si第j对交点孔-轴-孔配合中孔1、轴和孔2的公差带宽,其取值由状态索引向量确定;(δi,ja)0、(δi,jb)0和(δi,jc)0分别为孔1、轴和孔2的公差中心.则移形误差Δi,j的保证公差[13]为
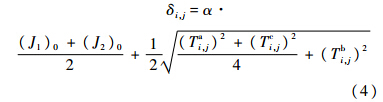
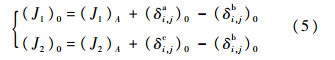
则由式(1)~式(5)可知,一旦确定交点的结构形式、几何参数、孔轴名义尺寸和公差配合,则采用概率法或极值法求解式(1)即可确定交点部件的协调误差:
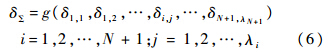
2 离散公差优化的动态规划模型
动态规划是解决多阶段最优化决策问题的一种方法,适用于有重叠子问题和最优子结构性质的问题.该方法将初始问题分解为多个相似的重叠子问题,通过存储、递归调用子问题的优化结果减少原始问题的计算量,算法效率上通常远低于朴素解法.对于飞机多交点装配公差优化问题,由于相邻交点移形环节采用同一交点孔,因此相邻移形环节公差配合的选择相互关联,具有显著的多阶段优化决策特征.以图 1为例,工装P1的交点孔公差在相邻移形环节“P0→P1”和“P1→P2”的取值是相同的,若“P0→P1”中交点孔-轴-孔配合为“H6/h5/H7”,则工装P1的交点孔公差“H7”约束了“P1→P2”环节的交点配合取值范围.另外,装配功能约束不要求公差设计遵循真实的交点移形顺序,因此相邻移形环节间公差配合取值约束是双向的.指定“P1→P2”环节中交点孔-轴-孔配合为“H7/g6/H8”后再确定“P0→P1”环节中配合为“H6/h5/H7”,与指定“P0→P1”环节中配合为“H6/h5/H7”后再确定“P1→P2”环节中配合为“H7/g6/H8”是等价的.
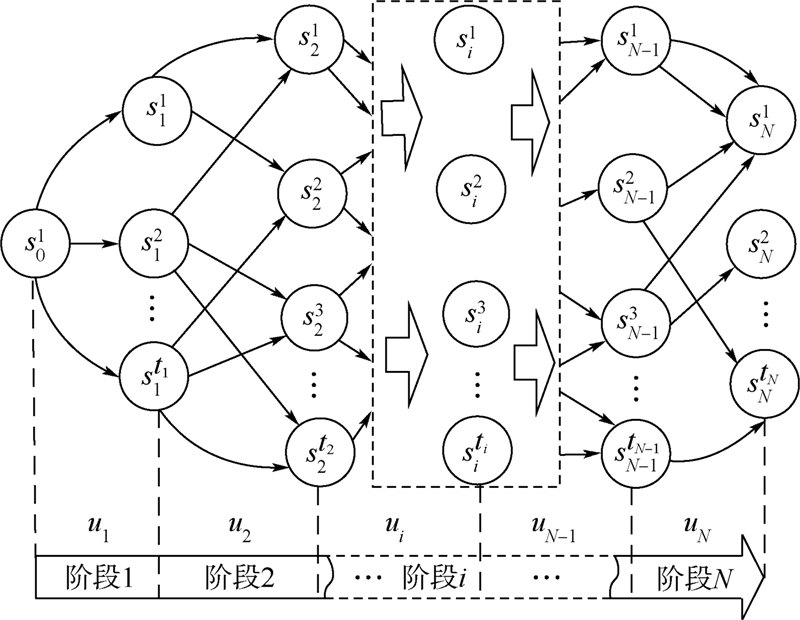
根据上述思路,采用有向图建立了多交点离散公差优化的动态规划模型,如图 4所示.该模型将多交点公差优化中的最优成本和装配性能计算作为可递归调用的重叠子问题建模,大大降低了公差优化算法的计算复杂度.该动态规划模型中的阶段、状态、决策和策略、状态转移和指标函数等关键要素定义如下:
1) 阶段:根据交点制造协调路线,将公差设计过程划分为N个阶段,每个阶段对应一对关联移形环节或协调环节的公差设计过程.
2) 状态:各阶段开始时的公差设计条件采用状态变量si来表示.图中第i列(i=1,2,…,N)节点表示状态i下所有可选公差配合的状态集合Si={si1,si2,…,siti},ti为状态集合的容量,第0列的节点s01为无实际意义的虚节点,显然有状态变量(公差配合取值)si∈Si.为确定各状态的顺序,由制造协调路线中的原始制造依据沿任一交点部件的制造协调路线单向逐环推进,每一移形环节或协调环节的公差配合视为一个状态,直到回到原始协调依据后结束推进.若状态i的移形环节有mi对交点配合可单独取值,则状态变量si可用唯一索引向量Di=[I1 I2 … Ik … Imi]表示其对应的公差配合值,其中索引值Ik∈{1,2,…,Qk}(k=1,2,…,mi)为第i对单独取值交点的取值索引,Qk为该交点的可选公差配合数目.显然,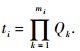
 |
| 图 4 多交点装配离散公差优化的动态规划模型Fig. 4 Dynamic programming model of discrete tolerance optimization for multi-joint assembly |
3) 决策和策略:状态i的状态变量si一旦确定,则可根据当前环节的公差配合对状态i+1的公差配合做出决策,记决策变量为ui(si).以状态变量si取值对应的节点为起点,其有向边集合记录了当前状态下所有可能决策集合,记为Di(si).显然,每一种决策变量ui(si)对应于图中的一条有向边,连接不同状态节点的有向边反映了相邻移形环节公差取值的约束关系.记策略变量为pi,N(i=1,2,…,N),表示由阶段i到阶段N所作决策构成的决策序列.
4) 状态转移:由于公差设计的多阶段决策中,下一阶段的状态变量si+1只取决于上一阶段的状态变量si和决策变量ui,则可定义状态转移方程为si+1=TiR(si,ui),其中TiR为状态转移函数.
5) 指标函数:公差优化的目标是成本最小化,阶段i的阶段成本指标函数定义为
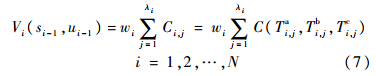
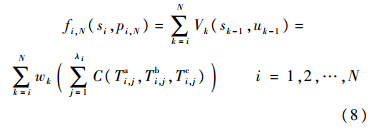
根据式(7)、式(8)和动态规划递推求解原理,最终公差成本优化的动态规划方程为
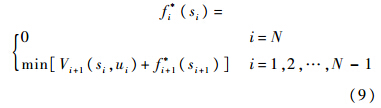
3 基于动态规划模型的公差优化
公差设计需满足飞机装配功能约束并具有最小化的公差成本,为约束多阶段优化问题.为上述动态规划模型引入装配性能指标表示装配功能对交点公差配合选择的约束,判定公差设计的可行性,在动态规划模型基础上利用分枝定界的思想[3]来分割解空间,减小公差择优的路径遍历复杂度.该公差优化过程包括“回溯”和“前溯”两个阶段.“回溯”阶段利用动态规划有向图模型逆序计算有向图中各节点后部子过程的最优成本和最优装配性能指标值;“前溯”阶段则是从有向图顺序查找装配功能约束下具有最小成本的公差解.
3.1 “回溯”阶段
“回溯”阶段的步骤为:
1) 引入装配性能指标函数的概念.采用概率法建立交点装配功能表达式,则阶段i的阶段装配性能指标函数定义为
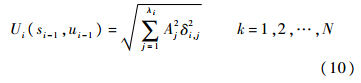
进而建立初始状态为si,采用策略pi,N时后部子过程的装配性能指标函数:
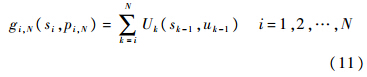
gi,N(si,pi,N)的值越小表示装配性能越高,用gi*(si)表示最优子过程的装配性能指标值.同理,建立装配性能优化的动态规划方程:
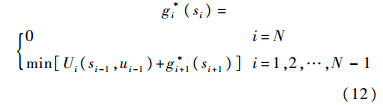
2) 定义有向图节点和有向边的属性值.有向图中每个状态变量si(i=0,1,…,N)的属性值用二元组(fi*,gi*)表示.同样,为图中决策变量ui(si)对应的有向边定义二元属性值(Vi,Ui).
3) 由式(7)和式(10)计算图中每条边的二元属性值(Vi,Ui),然后根据式(9)和式(12)“逆序”求解每个图节点的二元属性值(fi*,gi*).
3.2 “前溯”阶段
“前溯”阶段的步骤为
1) 变量定义和初始化.设装配精度指标为δ0,定义最优策略为p*0,N,其成本指标值为f*,装配性能指标为g*;定义较优成本指标fm和较优装配性能gm,表示包含既定决策序列p0,i的所有策略p0,N中最优的成本指标值和最优的装配值;决策过程采用有序队列组{Q0,Q1,…,QN}表示,Qi为存储第i个状态的待选状态节点序列.在公差存在可行解的情况下,令具有最优装配性能指标的策略p^0,N为初始解,其尺寸链成本为f 0,则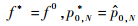 ;初始化f m=0,gm=0;初始各队列Qi为空;初始化状态i=0.
;初始化f m=0,gm=0;初始各队列Qi为空;初始化状态i=0.
2) 按照顺序状态i=0,1,…,N和深度优先策略进行图遍历,根据“入队”规则将各状态节点顺次加入队列组{Q0,Q1,…,QN}中.“入队”规则为:①当状态i=0时,直接将节点s01加入队列Q0.②当1≤i≤N时,依次查找节点集Si中与队列Qi-1队首节点边相连的所有节点,并计算每个节点的较优成本fm和极小装配误差gm:
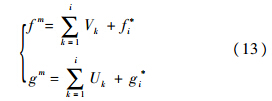
若fm<f*且gm≤δ0,则该节点加入队列Qi.若i=N,转步骤3);否则,令i=i+1,重复步骤2),继续下一阶段遍历.
3) 按照“出队”规则评价待选决策序列.“出队”规则为:①当Qi=Ø时,若i=0则转步骤4);否则,令i=i-1,弹出Qi队首节点,转步骤2).②当Qi≠Ø时,若i=N则依次取{Q0,Q1,…,QN}各队首节点构成的决策序列p0,N,若其尺寸链成本f0,N<f*,则令f*=f0,N,p*0,N=p0,N,弹出Qi队首节点,重复步骤3).
4) 结束图遍历,输出最优策略p*0,N.
4 实例分析
某型直升机尾梁和可折叠斜梁采用4对平面叉、耳接头进行装配连接,如图 5所示.位于尾梁和斜梁上的第1对交点和第3对交点的公称尺寸为18 mm;位于尾梁和斜梁上的第2对交点和第4对交点的公称尺寸为12 mm.为了保证接头的可靠定位、减少振动并防止自动解锁机构打开接头螺栓时可能出现的卡死问题,接头处采用了小间隙高精度等级的孔、轴配合,因此接头的制造协调准确度要求高.
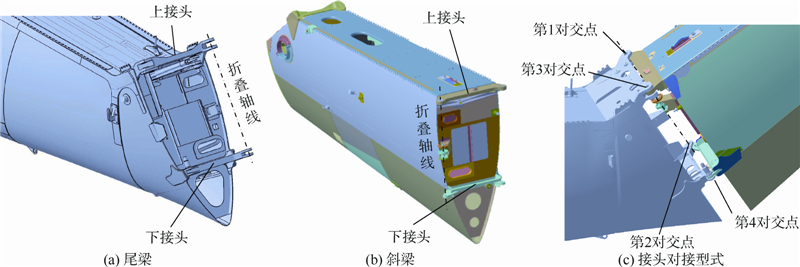 |
| 图 5 直升机尾梁、斜梁接头装配示意图Fig. 5 Assembly diagram of helicopter tail beam and inclined beam joints |
在制造工艺上,为了改善接头的制造工艺性和制造经济性,采用实物协调的制造方法分别制造尾梁、斜梁的上、下接头,其工艺协调路线如图 6所示.
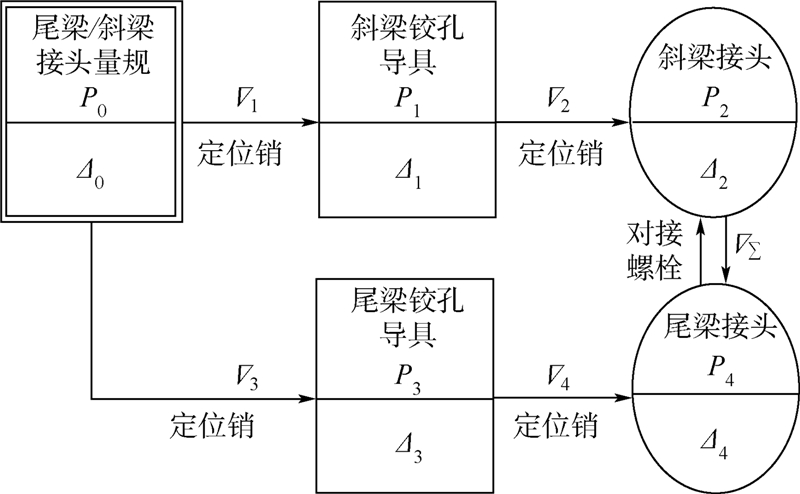 |
| 图 6 尾梁、斜梁交点对接协调路线图Fig. 6 Coordination route of tail beam and inclined beam joint butting |
在装配过程中,以第1~3对交点为基准交点连接后,再装配第4对交点,装配协调主要涉及第4对交点的同轴度误差控制,装配工艺规范规定第4对交点孔允许的最大协调误差δ0=0.15 mm.斜梁接头量规和尾梁接头量规采用同时镗孔的方法来消除两者的交点误差,因此在协调路线中把尾梁、斜梁量规看作同一移形单元.“P2P4”环节进行尾梁和斜梁对接时,采用了名义直径比接头孔名义直径小0.005 mm的对接螺栓来保证斜梁的折叠功能.公差设计时,首先由工艺员初步确定各环节孔、轴公差配合的备选集合,该集合的确定参照了飞机制造交点容差设计规范[13],有关孔、轴公差与配合的国家标准[14]以及工艺员的实际经验,详见表 1.其中,为了简化制造工艺,尾梁量规、斜梁量规、尾梁铰孔导具及斜梁铰孔导具的交点1与交点3,交点2与交点4要求选用相同的孔、轴公差配合.
相邻移形(协调)环节间公差配合取值约束是双向的,不影响最终的公差设计结果,建立交点离散公差优化的动态规划模型.该动态规划模型共包含6个状态(s0~s5),其中s0为初始状态,s1~s5分别对应尺寸移形(或协调)环节“P0→P1”、“P1→P2”、“P2 ↔ P4”、“P3→P4”和“P0→P3”的公差取值.状态si中各交点的独立公差配合变量组合构成状态集合Si,根据表 1中列举的可选配合可知,各状态的设计变量数目分别为t1=16、t2=16、t3=16、t4=16和t5=16.根据式(1)~式(3),可得尾梁、斜梁第4对交点协调误差:
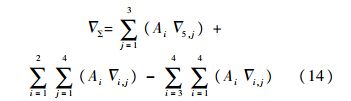
“回溯”时由式(7)和式(10)、式(9)和式(12)逆序求解动态规划图节点和边的属性值.
其中,交点装配系数分别为A1=0.91、A2=-1、A3=-0.91及A4=1.各交点保证公差δi,j由式(4)计算(令插孔修正系数α=0.5),而交点孔、轴的公差成本[15]分别为
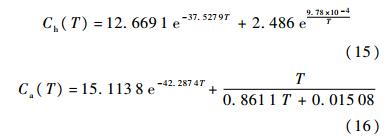
| 移形过程 | 交点对 | 交点孔、轴尺寸/mm | 可选公差配合 | |||||
| 孔1 | 轴 | 孔2 | ||||||
| P0→P1 | 1,3 | Ø18 | Ø18 | Ø18 | H6/h5/H7 | H7/f 6/H8 | H7/h6/H8 | H7/g6/H8 |
| 2,4 | Ø12 | Ø12 | Ø12 | H6/h5/H7 | H7/f 6/H8 | H7/h6/H8 | H7/g6/H8 | |
| P1→P2 | 1,3 | Ø18 | Ø18 | Ø18 | H7/h5/H8 | H7/h6/H8 | H8/h7/H9 | H8/f 7/H9 |
| 2 | Ø12 | Ø12 | Ø12 | H7/h5/H8 | H7/h6/H8 | H8/h7/H9 | H8/f 7/H9 | |
| 4 | Ø12 | Ø12 | Ø12 | 垂直铰孔自动对中,无移形误差;公差取值与第2对交点相同 | ||||
| P0→P3 | 1,3 | Ø18 | Ø18 | Ø18 | H6/h5/H7 | H7/f 6/H8 | H7/h6/H8 | H7/g6/H8 |
| 2,4 | Ø12 | Ø12 | Ø12 | H6/h5/H7 | H7/f 6/H8 | H7/h6/H8 | H7/g6/H8 | |
| P3→P4 | 1,3 | Ø18 | Ø18 | Ø18 | H7/h5/H8 | H7/h6/H8 | H8/h7/H9 | H8/f 7/H9 |
| 2 | Ø12 | Ø12 | Ø12 | H7/h5/H8 | H7/h6/H8 | H8/h7/H9 | H8/f 7/H9 | |
| 4 | Ø12 | Ø12 | Ø12 | 垂直铰孔自动对中,无移形误差;公差取值与第2对交点相同 | ||||
| P2→P4 | 1,3 | Ø18 | Ø17.995 | Ø18 | H8/f 7/H8 | H8/h7/H8 | H9/d9/H9 | H9/f 9/H9 |
| 2,4 | Ø12 | Ø11.995 | Ø12 | H8/f 7/H8 | H8/h7/H8 | H9/d9/H9 | H9/f 9/H9 | |
在“前溯”阶段中采用基于顺序队列组的有向图搜索算法求解具有最小成本且满足装配功能约束的最优策略p*0,6.公差优化的计算结果如表 2所示,优化得到的公差成本性能指标值f*=225.876,装配性能指标值g*=0.149 7 mm≤δ0,满足装配工艺规范对第4对交点孔的最大协调误差允许值(0.15 mm).
| 移形过程 | 交点对 | 孔、轴尺寸及优选公差/mm | 保证公差>δi,j/mm | 成本(Ci,j)×权值(wi) | 成本性能与装配性能指标值 | ||||
| 孔1 | 轴 | 孔2 | 孔1 | 轴 | 孔2 | ||||
| P0P1 | 1,3 | Ø18H6 | Ø18h5 | Ø18H7 | 0.012 2 | 11.101×0.3 | 11.140×0.3 | 9.072×0.7 | f*=225.876 g*=0.149 7 mm |
| 2,4 | Ø12H6 | Ø12h5 | Ø12H7 | 0.012 2 | 11.101×0.3 | 11.140×0.3 | 9.072×0.7 | ||
| P1→P2 | 1,3 | Ø18H7 | Ø18h6 | Ø18H8 | 0.018 2 | 9.072×0.7 | 9.940×0.7 | 7.180×1.0 | |
| 2 | Ø12H7 | Ø12h6 | Ø12H8 | 0.018 2 | 9.072×0.7 | 9.940×0.7 | 7.180×1.0 | ||
| 4 | Ø12H7 | Ø12h6 | Ø12H8 | 9.072×0.7 | 9.940×0.7 | 7.180×1.0 | |||
| P0→P3 | 1,3 | Ø18H6 | Ø18h5 | Ø18H7 | 0.012 2 | 11.101×0.3 | 11.140×0.3 | 9.072×0.7 | |
| 2,4 | Ø12H6 | Ø12h5 | Ø12H7 | 0.012 2 | 11.101×0.3 | 11.140×0.3 | 9.072×0.7 | ||
| P3→P4 | 1,3 | Ø18H7 | Ø18h6 | Ø18H8 | 0.018 2 | 9.072×0.7 | 9.940×0.7 | 7.180×1.0 | |
| 2 | Ø12H7 | Ø12h6 | Ø12H8 | 0.018 2 | 9.072×0.7 | 9.940×0.7 | 7.180×1.0 | ||
| 4 | Ø12H7 | Ø12h6 | Ø12H8 | 9.072×0.7 | 9.940×0.7 | 7.180×1.0 | |||
| P2→P4 | 1,3 | Ø18H8 | Ø17.995h7 | Ø18H8 | 0.026 9 | 7.180×1.0 | 7.650×1.0 | 7.180×1.0 | |
| 2 | Ø12H8 | Ø11.995h7 | Ø12H8 | 0.026 9 | 7.180×1.0 | 7.650×1.0 | 7.180×1.0 | ||
| 4 | Ø12H8 | Ø11.995h7 | Ø12H8 | ||||||
从算法效率上分析,与单纯的穷举搜索法对比,本例需要进行的搜索次数为165=1 048 576次(不考虑相邻环节的公差取值约束关系,每对交点的公差由可选公差配合中进行选择).而采用本文的方法利用相邻移形环节间的公差配合取值约束建立动态规划图,并基于动态规划模型进行公差优化值的启发式搜索时,“回溯”阶段图中边和节点搜索528次,“前溯”阶段图中节点搜索16 384次,总共搜索16 912次.由此可见,此方法有效提高了公差优化求解的效率.
5 结 论
1) 飞机多交点装配公差优化问题可采用基于有向图表达的动态规划模型进行描述,该模型体现了公差设计的多阶段决策特点,以及相邻尺寸协调环节间公差选择的约束关系,可有效避免各环节成本和装配性能的重复计算.
2) 基于成本指标和装配性能指标的最优公差启发式搜索算法,通过解空间的分割策略进一步提高公差寻优效率,有效提高了具有复杂尺寸协调环节的多交点装配公差设计问题的计算效率.
3) 基于动态规划的飞机多交点装配公差优化方法可保证所求公差解的全局最优性.
| [1] | Moy W A. Assignment of tolerances by dynamic programming[J].Machine Design,1968,21:215-218. |
| [2] | Smathers E W,Ostwald P F.Optimization of component functional dimensions and tolerances[J].Mechanical Engineering,1972,94(7):59. |
| [3] | Lee W J,Woo T C.Optimum selection of discrete tolerances[J].Journal of Mechanisms,Transmissions,and Automation in Design,1989,111(2):243-251. |
| Click to display the text | |
| [4] | Chase K W,Greenwood W H,Loosli B G,et al.Least cost tolerance allocation for mechanical assemblies with automated process selection[J].Manufacturing Review,1990,3(1):49-59. |
| Click to display the text | |
| [5] | Kusiak A,Feng C X.Deterministic tolerance synthesis:a comparative study[J].Computer-Aided Design,1995,27(10):759-768. |
| Click to display the text | |
| [6] | Deng J,Deng S.The adaptive branch and bound method of tolerance synthesis based on the reliability index[J].The International Journal of Advanced Manufacturing Technology,2002,20(3): 190-200. |
| Click to display the text | |
| [7] | Kumar M S,Kannan S M,Jayabalan V.A new algorithm for optimum tolerance allocation of complex assemblies with alternative processes selection[J].The International Journal of Advanced Manufacturing Technology,2009,40(7-8):819-836. |
| Click to display the text | |
| [8] | Xue J,Ji P.Process tolerance allocation in angular tolerance charting[J].International Journal of Production Research,2004,42(18):3929-3945. |
| Click to display the text | |
| [9] | Lööf J,Hermansson T,Söderberg R.An efficient solution to the discrete least-cost tolerance allocation problem with general loss functions[C]//Models for Computer Aided Tolerancing in Design and Manufacturing.Netherlands:Springer,2007:115-124. |
| Click to display the text | |
| [10] | Lööf J,Söderberg R.Discrete tolerance allocation for product families[J].Engineering Optimization,2012,44(1):75-85. |
| Click to display the text | |
| [11] | Sivakumar K,Balamurugan C,Ramabalan S.Concurrent multi-objective tolerance allocation of mechanical assemblies considering alternative manufacturing process selection[J].The International Journal of Advanced Manufacturing Technology,2011,53(5-8):711-732. |
| Click to display the text | |
| [12] | Geetha K,Ravindran D,Kumar M S,et al.Multi-objective optimization for optimum tolerance synthesis with process and machine selection using a genetic algorithm[J].The International Journal of Advanced Manufacturing Technology,2013,67(9-12):2439-2457. |
| Click to display the text | |
| [13] | 程宝蕖. 飞机制造协调准确度与容差分配[M].北京:航空工业出版社,1987:116-140. Cheng B Q.Aircraft manufacturing coordination accuracy and tolerance allocation[M].Beijing:Aviation Industry Press,1987:116-140(in Chinese). |
| [14] | 中华人民共 和国国家质量监督检验检疫总局.GB/T 1801—2009产品几何技术规范(GPS)极限与配合公差带和配合的选择[S].北京:中国标准出版社,2009. The State Administration of Quality Supervision,Inspection and Quarantine of the People's Republic of China.GB/T 1801—2009 Geometrical product specifications(GPS)—Limits and fits—Selection of tolerance zones and fits[S].Beijing:Standards Press of China,2009(in Chinese). |
| [15] | 吴昭同,杨将新. 计算机辅助公差优化设计[M].杭州:浙江大学出版社,1999:66-69. Wu Z T,Yang J X.Computer-aided tolerance optimization[M].Hangzhou:Zhejiang University Press,1999:66-69(in Chinese). |



