压力传感器广泛应用于航空航天运载系统、战术导弹、遥感测量、火炮装备及船舶制造等领域[1, 2];实际工程中的许多物理量,如液位、流量、飞行速度和飞行高度等,也可以通过压力传感器来间接测量[3].使用压力传感器实时、可靠地跟踪被测信号的变化、获得准确的测量结果,这就要求开展动态校准、准确掌握传感器动态参数指标.
压力传感器的动态校准是保证动态测试数据准确与可靠的重要前提[1, 3, 4].相对于静态测量而言,动态测量的发展历史还比较短,加之动态测量的环境也更加复杂、条件更加苛刻,这也决定了压力传感器的动态校准是一个比较复杂的过程.这种复杂性决定了压力传感器校准结果不可避免地具有不确定度,加之在实际校准测试中依旧是处于“以静代动”的水平[5],而且评定人员的主观经验和知识水平参差不齐,致使校准不确定度的因素呈现多样性和复杂性,导致压力传感器测量校准的结果相差十分悬殊[3, 4, 5, 6].随着工业需求对压力传感器测量结果的准确性与可靠程度要求越来越高,这就对压力传感器校准不确定度评定也提出了更高的要求.对动态校准数据的不确定度分析,与静态测量相比要复杂和困难得多,目前在实际的测量工作中很难给出通用的压力传感器动态校准不确定度评定准则[3, 5].
不确定度评定是压力传感器动态校准中的关键点[1, 5].目前,在这方面国内外学者已经作了少量的研究,并取得了一定的成果.国际上开展压力的动态测量校准方面研究相对较早.20世纪60年代美国颁布了压力传感器动态校准规范ANSI B88.1—1972A,这是首个压力传感器动态校准的专业标准[7].1986年,国际计量委员会(Comité International des Poids et Mesures,CIPM)以ISO名义颁布了测量不确定度指南(Guide to the Uncertainty in Measurement,GUM),这对校准不确定度评定具有里程碑的意义[3, 5, 7].著名学者Martz认为,在单次动态校准数据较少情况下,其评定如使用统计学和概率论的方法应斟酌[8].美国人Crowder[9]首次将蒙特卡洛法引入了动态校准不确定度评定,构建了新的评定思路.文献[10]提出从校准实验的误差源着手,对影响校准精度的几个主要因素进行了分析,建立了各因素的不确定度传播方程,最后通过合成求得总的校准不确定度;它为动态校准不确定度的评定提供了一条新的途径,但是该法的局限性在于所得不确定度结果可靠性过分依赖误差分析的结论,而误差分析及合成中的权重分配主观性强,很多是基于经验分析;另外,不同实验条件下各误差源的影响会改变,使得该法的通用性较差.文献[11]采用比较法原理,对被校准压力传感器频域特征的测量不确定度进行了评定,实现过程简洁;但是,该法的不足是评定精度严重依赖于标准传感器,当标准传感器的精度与被校准的相近时,不确定度评定的可靠性难以保证.
国内方面,夏新涛等将模糊理论和贝叶斯理论有机融合,应用到动态测量不确定被评定中[12, 13];王中宇等[14, 15, 16]将灰色系统理论引入动态测量误差的评定,该理论利用已有测量数据预测生成新的信息,开辟了一条解决动态测量不确定度评定问题的新途径.费业泰[17]与盛克仁[18]使用灰色方法实现了动态测量不确定度评定,评定精度与传统方法相近.袁俊先和蔡菁[19]主要针对被校准压力传感器的幅值灵敏度指标进行评定,在假设各校准影响指标相互独立的基础上,合成不确定度值,所采用的处理思路和文献[10]类似.张力[20]提出用最小二乘法求出传感器的理想特性曲线,通过与实际校准所得数据相比较,求出两条曲线间的差值即为不确定度,该法摆脱了对具体影响因素的依赖;所采用的等权拟合,使得部分测量效果较差的频率点数据对合成的曲线形状影响难以约束,致使曲线模型的可靠性难以保障.黄俊钦[5]在深入分析校准影响源的情况下,提出了一种基于数据分析的评定压力传感器动态校准不确定度的新方法,给出了详细求解步骤,丰富了压力传感器不确定度评定方法;但该方法并非完全意义上的动态不确定度评定方法,它只能计算测量频率点的校准不确定度,对于没有测量数据的频率点难以评定,因而难以实现被校准压力传感器全工作频段的不确定度评定.依据中国动态压力传感器检定规程(JJG 624—2005)[21],若使用其指定的少量频率点数据,现有基于统计理论的分析方法很难实现其全频段动态校准不确定度评定.
目前,综合国内外的发展现状,还没有出现一种简单、通用性强的动态不确定度分析方法,用于解决压力传感器动态校准所用频率点不确定度的可靠评定问题.本文提出一种用于压力传感器动态校准不确定度的灰色评定方法,其核心思想是有机结合灰色系统理论[22, 23]的累加生成、灰关联分析和灰色GM(0,2)模型等相关内容,发掘被校压力传感器动态校准数据随频率变化而包含的内在规律性、不同频率点测量数据的关联性以及动态校准数据的变化趋势,将所得信息用于加权最小二乘建模,得出被校压力传感器在工作频率范围内的测量不确定度变化规律.
1 动态校准不确定度评定 1.1 评定原理
压力传感器动态校准不确定度的灰色评定过程包括如下几个步骤:
1) 选定压力驱动源并指定校准频率点,采样被校准压力传感器的输出.
2) 对采样输出序列进行灰色关联分析,求得指定频率点在多次重复校准中输出值的权重系数.
3) 对多列输出数列进行处理,生成被校准压力传感器特征序列,进而对数据进行累加生成、灰系数计算.
4) 利用得到的累加生成序列和灰色系数构建灰色偏度评定模型,得到各指定校准频率点的灰色偏度.
5) 结合已得到的权重系数,应用神经网络拟合法对各频率点的灰色偏度值进行拟合,估计出被校准压力传感器在全工作频段的动态校准不确定度.
评定原理的如图 1所示.
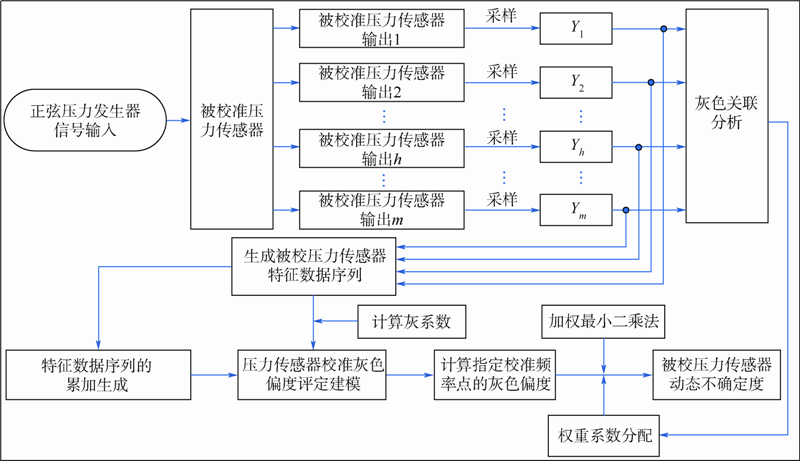 |
| 图 1 压力传感器动态校准不确定度的灰色评定原理Fig. 1 Principle of grey method (GM) for dynamic uncertainty evaluation of calibrated pressure transducer |
压力传感器的动态校准是一个动态重复测量的过程,被校准压力传感器的输出可以看作是3部分响应的合成:对正弦激励的响应、系统误差的响应和随机测量误差的响应[1, 8, 14, 17, 24].通常,传感器测量输出数据中的系统误差易于剔除,因此在本文中,压力传感器动态校准不确定度灰色评定的主要任务就是获取传感器性能在随机误差影响下的变化规律.
依据中国动态压力传感器检定规程(JJG 624—2005)的规定,进行动态校准时需依据被校准压力传感器工作频率范围设定校准的频率点.在此,假设设定N个校准频率点{P1,P2,…,Pk,…,Pn},且P1<P2<…<Pk<…
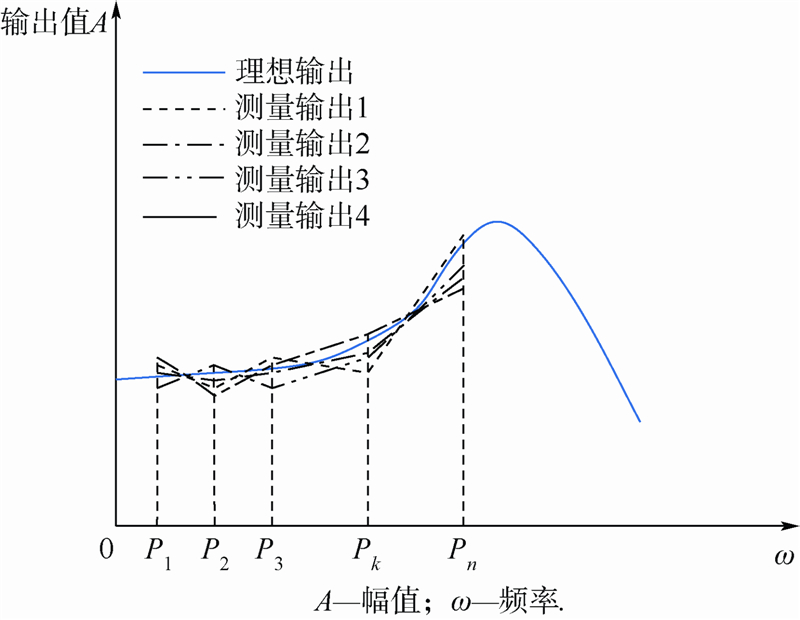 |
| 图 2 压力传感器动态校准的输出Fig. 2 Output of dynamic repeated calibration for pressure transducer |
为了定量化描述图 2中所包含的校准不确定度,设激励输入为x(P),P为校准频率点;被校准压力传感器在x(P)信号激励下产生输出,剔除系统误差后,得到表征传感器动态特性的输出数据x(P),这时的x(P)即为对输入激励x(P)的稳态响应和随机测量误差的合成,相关含义可以用式(1)表示.
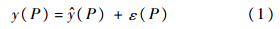
设对某压力传感器进行m次校准实验,以其校准频率点Pk为例,如果发现在该处的随机误差服从正态分布(如图 3所示),那么在该校准过程中,需计算出在该频率点的灰色偏度,进而评估在此处的校准不确定度.
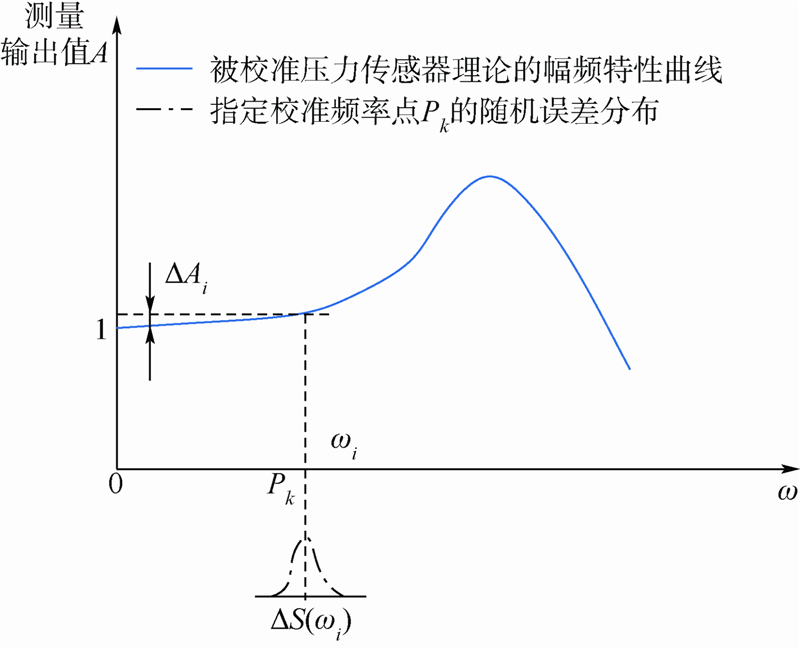 |
| 图 3 压力传感器动态校准不确定度Fig. 3 Dynamic calibration uncertainty for pressure transducer |
设压力传感器的校准过程重复了m次,得到输出相应数据y1(P),y2(P),…,yh(P),…,ym(P).以校准频率点的形式可表示为
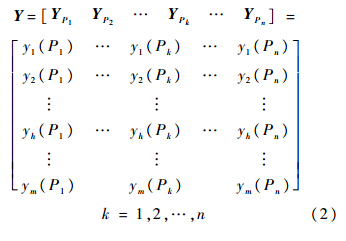
首先,对同一校准频率点的激励响应数据进行均值化处理:
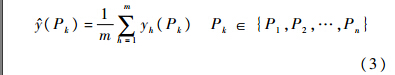
如果在指定校准频率点Pk的测量输出数据不存在任何随机误差,那么被校准压力传感器的测量输出即为测量真值.这些测量数据就可以组成如下测量值序列:

对序列y(0)Pk进行一次累加生成处理(1-AGO):

进行上述处理后得到数列y(1)Pk={APk,2APk,…,nAPk}.由于不存在任何随机误差,因此在指定频率点Pk的测量序列经过累加处理后所得结果为一条直线,直线方程可表示为

实际上,被校准压力传感器在任何指定校准频率点的测量输出数据不可能没有随机误差,该误差使得测量值偏离真值.设在指定校准频率点Pk的输出真值为APk,将m次重复测量输出值以升序排列可组成式(7)的数列:
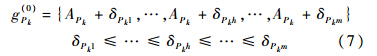
对式(7)中的测量输出序列进行一次累加生成(1-AGO),得到累加序列{g(1)Pk(h)}:
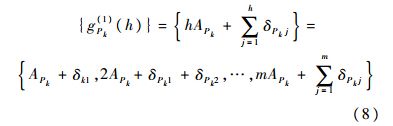
式(9)为序列{g(1)Pk(h)}与序列{y(1)Pk(h)}对于成员差值,表示测量累加曲线与式(6)所表示直线间的距离,图 4详细描述了它们之间的关系.

依据最大距离ΔPkmax和重复测量次数m,可以构建在指定校准频率点的灰色偏度评价模型为



 |
| 图 4 校准频率点Pk在m次测量下的灰偏差Fig. 4 Grey discrimination of measurement error for frequency Pk with m times of measurements |
用式(10),可以算出在所有指定校准频率点{P1,P2,…,Pk,…,Pn}的灰色偏度序列{σP1,σP2,…,σPk,…,σPn}.
基于灰色关联分析[14, 15, 17, 18, 22, 23],定义灰关系常数序列γ:


定义灰色偏度序列{σP1,σP2,…,σPk,…,σPn}中各元素的权重系数为


以W为权值,使用加权最小二乘法对灰色偏度序列{σP1,σP2,…,σPk,…,σPn}拟合,其终止条件为

通过上述拟合,最终得到被校准传感器动态校准不确定模型.
1.3 灰常量c的计算
灰常量的计算流程如图 5所示.首先将测量输出数组中任意随机提取N个数据样本;然后取前m个,计算S(1),D(1)通过式(9)、式(10)和式(11)得到;依此可以计算出前m+1个数据的S(2)、D(2),依此直到N,得到S(1)、S(2)、S(N-m+1),D(1)、D(2)、D(N-m+1);将S序列和D序列进行一次累加生成处理,得到对应序列X1(1)和X2(1),以这两个序列构建GM(0,2)模型:

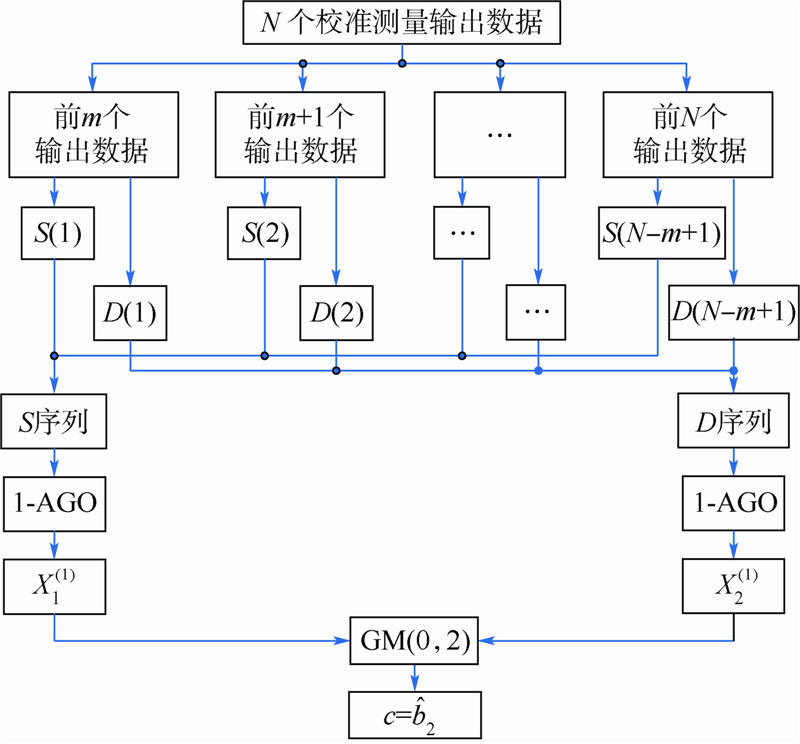 |
| 图 5 灰常量c的计算流程Fig. 5 Calculation flowchart of grey constant c |
2 实例分析
被校准压力传感器型号为恩德福克8510C,其工作频率范围为[1,1 100]Hz,所能承受的最大压力为2.5 MPa;该压力传感器的校准压力源选用SY-10型正弦压力发生器,其关键技术指标如表 1所示.依据中国计量规程JJG 624—2005,设置8510C型压力传感器的校准频率点为:8,32,80,160,250,400,600,800和1 000 Hz,每个校准点重复测量6次,实验环境如图 6所示.除依据规程JJG 624—2005设置的校准点外,另行设置测试频率点:16,100,300,700和900 Hz,用以检验本文所提方法得到的动态校准不确定度在全工作频段的评估效果.
| 指标类型 | 取值范围 |
| 校准压力范围/MPa | 0~10 |
| 工作频率范围/Hz | 0.1~2 000 |
| 波形失真度/% | 3~5 |
 |
| 图 6 测量实验环境Fig. 6 Environment of measurement test |
为了更加完备地验证本文所提校准不确定度评估方法的可靠性,在频率点设定的基础上,制定两套实验方案:①用本文所提灰方法评估在压力幅值变化情况下的不确定度;②在压力幅值不变情况下,用本文所提灰方法进行不确定度评估.
2.1 幅值变化情况下的校准不确定度评定
首先进行方案①实验(即压力幅值变化情况下的被校准压力传感器特征数据的不确定度评定).幅值设定的变化规律为:随着频率数据的增大,幅值也相应变大,目的是为了让评估方法突显出在频率逐渐增大情况下,校准对幅值的影响;各频率点对应的变化压力幅值如表 2所示.
被校准压力传感器在各频率点的幅值响应数据经过无量纲化处理后,得到如图 7所示的实验数据.进行无量纲化处理时,选取在频率点8 Hz处、在压力幅值0.50 MPa激励下,6次重复校准下压力传感器最小响应数据为基值,用变化压力幅值激励下的各个频率点的输出均除以该基值.
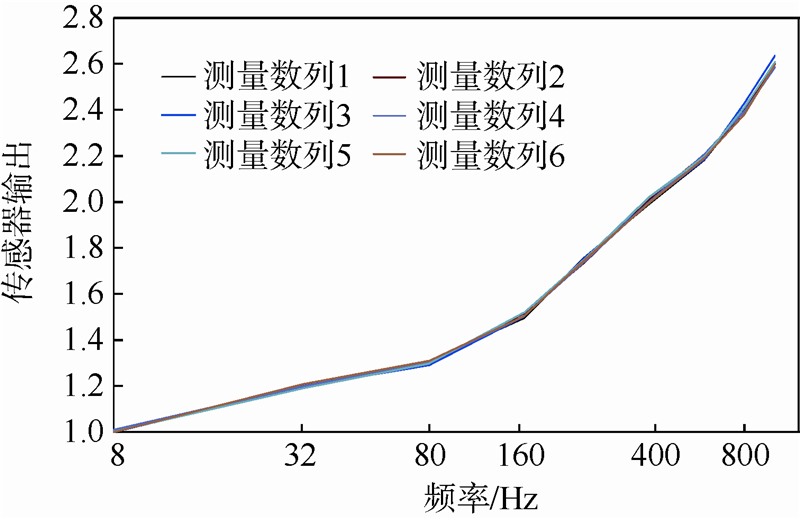 |
| 图 7 被校准传感器8510C在幅值变化下的 幅值响应输出数据Fig. 7 Amplitude measurements of calibrated 8510C transducer under changing input |
从图 7中数据可以看出,随着频率增大相应幅值响应也从1.000 0逐渐增大;并且随着输出频率增大同一频率点重复测量响应数据的发散性有所增强,这种发散性正是本文所提方法要定量化评定的内容.
使用图 7中8,32,80,160,250,400,600,800和1 000 Hz的输出数据序列按照图 5流程,分别构建GM(0,2)模型,求出相应c值如表 2所示.依据表 2数据结合各频率点所得测量数列,构建各自灰色评定模型,求出了各指定频率点测量灰色偏度如表 3所示.
| 参数 | Pk/Hz | ||||||||
| 8 | 32 | 80 | 160 | 250 | 400 | 600 | 800 | 1 000 | |
| 压力幅值/MPa | 0.50 | 0.60 | 0.65 | 0.75 | 0.88 | 1.00 | 1.10 | 1.20 | 1.30 |
| c | 2.411 | 2.423 | 2.431 | 2.400 | 2.436 | 2.417 | 2.428 | 2.425 | 2.419 |
| Pk/Hz | 8 | 32 | 80 | 160 | 250 | 400 | 600 | 800 | 1 000 |
| 灰色偏度 | 0.005 0 | 0.004 7 | 0.003 9 | 0.003 7 | 0.003 0 | 0.003 8 | 0.003 9 | 0.006 9 | 0.007 4 |
通过灰关联分析,得出各指定校准频率点的权重分析系数,如表 4所示.从8 Hz开始,权重系数随着频率增大而变大,说明测量数据较可靠;但是当到400 Hz时权重系数开始逐渐减小,这也说明频率增大时校准影响因素的作用变强,数据的可信度变弱.
| Pk/Hz | 8 | 32 | 80 | 160 | 250 | 400 | 600 | 800 | 1 000 |
| 权重系数 | 0.089 9 | 0.100 7 | 0.107 9 | 0.111 5 | 0.125 9 | 0.136 7 | 0.122 3 | 0.111 5 | 0.093 5 |
由表 3和表 4数据,构建加权最小二乘拟合,得出表征被校准压力传感器动态不确定度的曲线模型.
2.2 幅值不变情况下的校准不确定度评定
在进行方案②验证实验时,将各个校准频率施加压力幅值设为固定值,均为0.80 MPa.传感器的幅值输出响应数据如图 8所示.
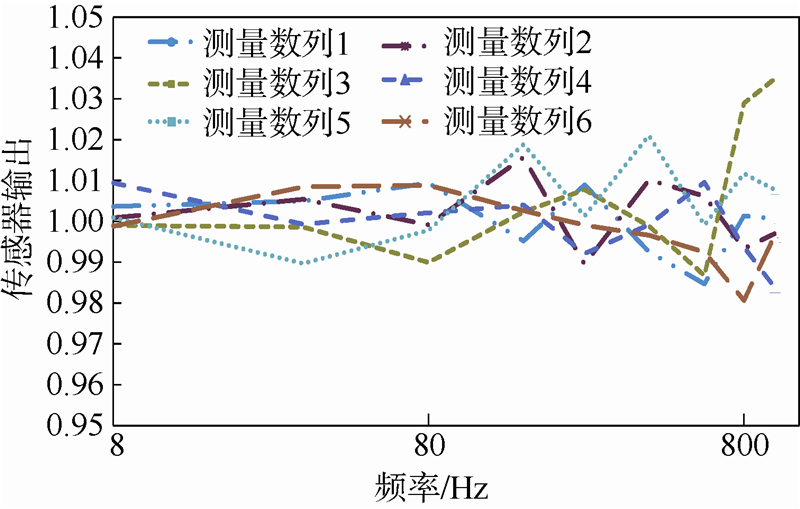 |
| 图 8 被校准传感器8510C在幅值不变情况下的 幅值响应输出数据Fig. 8 Amplitude measurements of calibrated 8510C transducer under unchanging input |
具体处理方式与2.1节相似.通过对图 8中各指定频率点数据构建GM(0,2)模型可以求得灰常量c值;依据c值构建灰色模型,得到各指定频率点的灰色偏度;之后通过关联分析得到了各指定频率点的权重分析系数;依据灰色偏度及权重系数信息进行加权最小拟合,最终得到了在压力幅值不变条件下被校准压力传感器动态不确定的曲线模型(如图 9所示的点线).
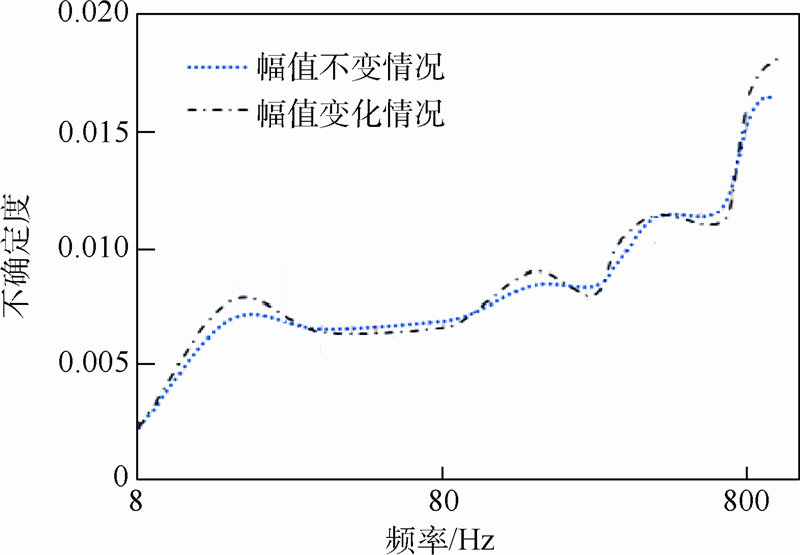 |
| 图 9 不同幅值条件下所得被校准8510C压力传感器的 动态校准不确定度Fig. 9 Dynamic uncertainty of the calibrated 8510C transducer under different amplitudes |
由表 3和表 4数据,构建加权最小二乘拟合,得到了在压力幅值变化条件下被校准压力传感器动态不确定的曲线模型(如图 9所示).对比在不同幅值条件下所得的两个曲线模型可以发现,幅值变化条件下所得曲线的波动性相对较强,这主要是压力幅值增大正弦压力源波形稳定性变弱造成的.另外,在变压力幅值的作用下,振动、温度变化等外界影响增大,使得校准效果恶化.对比图 9中两条曲线之间的形状还可以看出,随着频率的增大,两个曲线模型的变化趋势是非常相近的,说明两种情况下所得的不确定度曲线模型具有一致性,证明在幅值变化与不变的条件下均可进行校准的不确定度评估;最后,两条曲线模型随频率增大不确定度逐渐变得的特征趋势说明,随着校准的频率增大,被校准压力传感器的测量能力逐渐变差,动态测量结果的失真变大.
为了验证在幅值变化情况下所得模型的准确性,基于图 7及表 5中的数据,运用黄俊钦所提出动态不确定度评估方法(本文简称黄方法)[5],分别计算在指定频率点:8,32,80,160,250,400,600,800,1 000 Hz及在测试频率点:16,100,300,700和900 Hz处的测量不确定度.
| Pk/Hz | 幅值/MPa | 被校准压力传感器的输出数据 | |||||
| 次数1 | 次数2 | 次数3 | 次数4 | 次数5 | 次数6 | ||
| 16 | 0.55 | 1.094 4 | 1.094 8 | 1.111 9 | 1.110 2 | 1.083 3 | 1.096 5 |
| 100 | 0.70 | 1.405 9 | 1.394 8 | 1.420 5 | 1.411 2 | 1.400 2 | 1.403 3 |
| 300 | 0.92 | 1.832 1 | 1.858 4 | 1.857 9 | 1.838 9 | 1.865 2 | 1.834 7 |
| 700 | 1.15 | 2.296 8 | 2.311 9 | 2.283 9 | 2.300 1 | 2.302 8 | 2.299 3 |
| 900 | 1.25 | 2.496 3 | 2.504 9 | 2.503 0 | 2.500 6 | 2.498 3 | 2.506 0 |
测量频率点包含测试频率点和依据规程JJG 624—2005设置的校准点.图 10为使用黄方法得到测量频率点不确定度数据以及两种方法在测量频率点得到不确定的差值的绝对值.
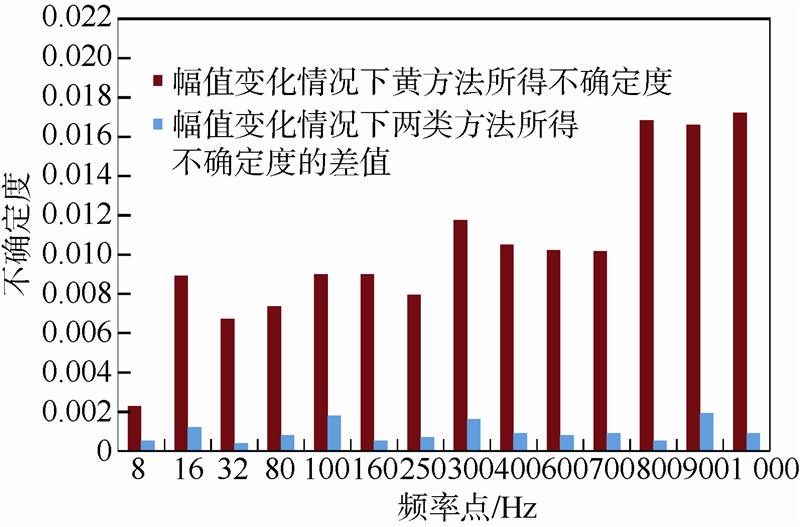 |
| 图 10 幅值变化条件下两种方法所得测量不确定度的对比Fig. 10 Uncertainty comparison obtained by different methods under changing input |
在图 10中的指定校准频率点处,按照本文的灰方法所得校准不确定度与黄方法所得结果的差值的绝对值小于0.001,对应相对误差不大于6%.在测试校准点,两种方法所得结果的差值虽然大于指定校准频率点,但是差值是处于可接受的范围内,对应相对误差小于10%.两类频率点处所得不确定结果的对比说明了灰方法评定结果的准确性和有效性,也说明在幅值变化的条件下,可以实现动态不确定度的评估.
为了验证在幅值不变情况下所得动态不确定度模型的准确性,基于图 8及表 6中的测量数据,同时运用黄方法计算在指定频率点及测试频率点的不确定度.灰方法与黄方法所得结果的对比如图 11所示. 图 11中包含使用黄方法得到的各测量频率点不确定度,以及点线模型(幅值不变化情况下所得的动态不确定度模型)与黄方法在各测量频率点得到不确定的差值的绝对值.从图 11可以看出,两种方法在测试频率点的差值相对较大,但是都小于0.001,它们明显小于图 10中同类型的差值.另外,在指定校准频率点,绝大部分差值都明显小于0.001,与黄方法所得不确定度相比,大部分指定校准频率点的相对误差小于5%,部分频率点的相对误差优于0.018%.在幅值不变的条件下,两类频率点处所得不确定结果的对比说明,本文所提压力传感器的动态校准不确定度评定方法能有效地实现其评估.
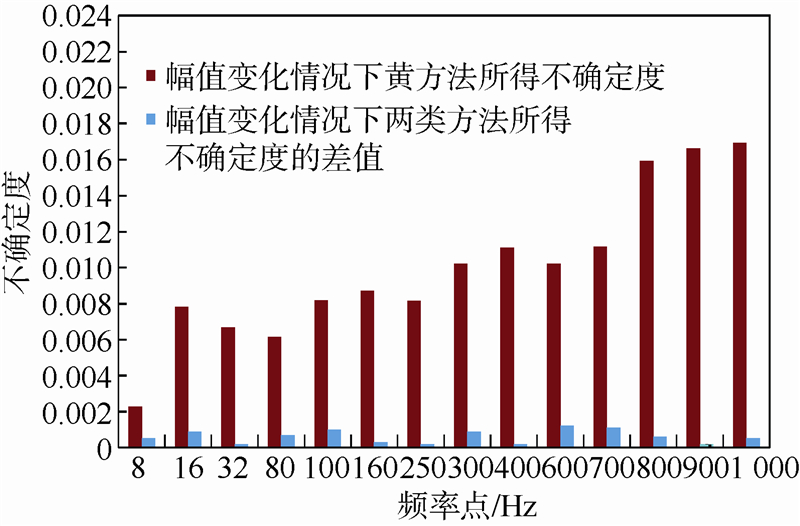 |
| 图 11 幅值不变条件下两种方法所得测量不确定度的对比Fig. 11 Uncertainty comparison obtained by different method under unchanging input |
| Pk/Hz | 幅值/MPa | 被校准压力传感器的输出数据 | |||||
| 次数1 | 次数2 | 次数3 | 次数4 | 次数5 | 次数6 | ||
| 16 | 0.80 | 1.579 6 | 1.578 8 | 1.582 0 | 1.593 4 | 1.576 0 | 1.569 8 |
| 100 | 0.80 | 1.580 0 | 1.589 3 | 1.582 8 | 1.568 8 | 1.568 9 | 1.582 0 |
| 300 | 0.80 | 1.589 0 | 1.570 6 | 1.580 3 | 1.570 0 | 1.583 7 | 1.596 0 |
| 700 | 0.80 | 1.568 7 | 1.591 2 | 1.576 9 | 1.591 9 | 1.578 9 | 1.598 2 |
| 900 | 0.80 | 1.562 1 | 1.590 9 | 1.570 8 | 1.598 5 | 1.560 5 | 1.561 3 |
在幅值变化与不变情况下分析表明,在进行压力传感器校准不确定度实验时,相对于变化幅值的激励而言,幅值不变或变化较小时,可以更准确地获得动态校准不确定度变化规律.另外,从两种实验方案下不同处理方法所得结论也可以看出,通用的黄方法相对于本文所提的灰方法而言,前者只能实现测量频率点的不确定度评定,不能实现非测量频率点不确定度预测.
3 结 论
鉴于压力传感器动态校准的原理和特点,本文在灰色系统理论的基础上,结合加权最小二乘法,提出了压力传感器动态校准不确定度的灰色评价模型,模型的动态评定效果在实际的校准中得到了有效验证.
1) 依据国家校准规程,本文所提出动态校准不确定度灰色评定方法,在不增加校准点数目的情况下,可实现校准不确定度的动态评定;是在现有规程条件下,对其确定度评定的有价值完善.
2) 所提灰方法能利用少量的指定校准点数据对被校准压力传感器的所有频率点的校准不确定度进行估计,表征被校准传感器的精度随频率变化规律,为压力传感器动态校准的误差溯源和误差修正奠定基础.
3) 本文所提灰方法克服了现有方法只能实现被测量校准点(包含指定校准点和测试点)不确定度评估的局限性;与其他传统方法相比,本方法在指定校准点所得不确定度与它们所得结果非常相近,在测试校准点也有很好的一致性.
4) 相对于变化的幅值激励而言,幅值不变或变化较小时,实验条件对校准结果的影响较弱,与黄方法相比,所得不确定度差值小于0.000 1,部分校准频率点的相对误差优于0.018%.基于所得到的被校准压力传感器的动态不确定度可知,在幅值激励不变或变化较小时,能更好地激发被校准传感器的动态特征,这有利于获取被校准动态校准不确定度的变化规律.
| [1] | Zheng D Z,Wu Z L,Yan Q,et al.Dynamic performance improvement on resonant vibration cylinder pressure transducer[J].Advanced Science Letters.2011,4(4-5):1376-1380. |
| Click to display the text | |
| [2] | Sharifian S A,Buttsworth D R.Evaluation of glued-diaphragm fibre optic pressure sensors in a shock tube[J].Shock Waves,2007,16(3):189-197. |
| Click to display the text | |
| [3] | Skoglund M, Pettersson M.A calibration scheme for imperfect quantizers[J].IEEE Transactions on Instrumentation and Measurement,2000,49(5):1063-1068. |
| Click to display the text | |
| [4] | Medawar S,Handel P,Murmann B,et al.Dynamic calibration of undersampled pipelined ADCs by frequency domain filtering[J].IEEE Transactions on Instrumentation and Measurement,2013,62(7):1882-1891. |
| Click to display the text | Cited By in Cnki (17) | |
| [5] | 黄俊钦. 动态不确定度的估算方法和应用实例[J].计量学报,2005,26(4):372-375. Huang J Q.The estimation method and application of dynamic uncertainty[J].Acta Metrologica Sinica,2005,26(4):372-375(in Chinese). |
| Click to display the text | Cited By in Cnki (5) | |
| [6] | 黄俊钦. 测温系统动态校准结果的不确定度估[J].仪器仪表学报,2008,29(4):870-873. Huang J Q.Dynamic uncertainty estimation of dynamic calibration results in temperature measurement system[J].Chinese Journal of Scientific Instrument,2008,29(4):870-873(in Chinese). |
| Click to display the text | Cited By in Cnki (5) | |
| [7] | Zhang Y,Zu J,Zhang H Y.Dynamic calibration method of high-pressure transducer based on quasi-delta function excitation source[J].Measurement,2012,45(8):1981-1988. |
| Click to display the text | |
| [8] | Martz Jr H F,Waller R A. Bayessian zero-failure (BAZE) reliability demonstration test procedure[J]. Journal of Quality Technology,1979,11(3):128-137. |
| Click to display the text | |
| [9] | Crowder S V,Moyer R D.A two-stage Monte Carlo approach to the expression of uncertainty with non-linear measurement equation and small sample size[J].Metrologia,2006,43(1):34-41. |
| Click to display the text | |
| [10] | Miura T,Huete A R,Yoshioka H.Evaluation of sensor calibration uncertainties on vegetation indices for MODIS[J].IEEE Transactions on Geoscience and Remote Sensing,2000,38(3):1399-1409. |
| Click to display the text | |
| [11] | Yadav S,Kumaraswamy B V,Gupta V K,et al.Least squares best fit line method for the evaluation of measurement uncertainty with electromechanical transducers (EMT) with electrical outputs (EO)[J].Mapan Journal of Metrology Society of India,2010,25(2):97-106. |
| Click to display the text | Cited By in Cnki (0) | |
| [12] | Xia X T,Wang Z Y,Gao Y S.Estimation of non-statistical uncertainty using fuzzy-set theory[J].Measurement Science and Technology,2000,11(4):430-435. |
| Click to display the text | |
| [13] | Xia X T,Chen X Y,Zhang Y Z,et al.Grey bootstrap method of evaluation of uncertainty in dynamic measurement[J].Measurement,2008,41(6):687-696. |
| Click to display the text | |
| [14] | 王中宇,刘智敏,夏新涛.测量误差与不确定度评定[M].北京:科学出版社,2008:35-40. Wang Z Y,Liu Z M,Xia X T.Measurement error and uncertainty evaluation[M].Beijing:Science Press,2008:35-40(in Chinese). |
| [15] | Wang Z Y,Ge L Y.Novel method of evaluating dynamic repeated measurement uncertainty[J].Journal of Testing and Evaluation,2008,36(5):453-459. |
| [16] | Qin P,Shen Y,Wang Z Y.Grey evaluation of non-statistical uncertainty in multidimensional precision measurement[J].The International Journal of Advanced Manufacturing Technology,2006,31(5-6):539-545. |
| [17] | 费业泰. 误差理论与数据处理[M].北京:机械工业出版社,2005:23-26. Fei Y T.Error theory and data processing[M].Beijing:Machinery Industry Press,2005:23-26(in Chinese). |
| [18] | 盛克仁. 过程测量仪表[M].北京:化学工业出版社,1992:15-18. Sheng K R.Process measuring instruments[M].Beijing:Chemical Industry Press,1992:15-18(in Chinese). |
| [19] | 袁俊先,蔡菁. 基于正弦压力校准装置的压力传感器不确定度评定[J].计测技术,2013(S1):190-192. Yuan J X,Cai J.Uncetainty evaluation for pressure transducer based on the sine pressure generator[J].Testing Technology,2013(S1):190-192(in Chinese). |
| Click to display the text | |
| [20] | 张力. 正弦压力校准测量不确定度分析[C]//压力计量服务和测试技术研讨会论文集.北京:中国计量测试学会,2003:26-32. Zhang L.Evaluation of uncertainty of sinusoidal pressure calibration[C]//Pressure Measurement Services and Test Technology Seminar Proceedings.Beijing:Chinese Society for Measurement,2003:26-32(in Chinese). |
| Click to display the text | |
| [21] | JJG 624—2005 动态压力传感器检定规程[S].北京:机械工业出版社,2005:5-9. JJG 624—2005 Verification regulation of dynamic pressure transducers[S].Beijing:Machinery Industry Press,2005:5-9(in Chinese). |
| [22] | 刘思峰,党耀国,方志耕,等.灰色系统:理论与应用[M].北京:科学出版社,2010:5-10. Liu S F,Dang Y G,Fang Z G,et al.The grey system: theory and its application[M].Beijing:Science Press,2010:5-10(in Chinese). |
| [23] | Liu S F. On measure of grey information[J].The Journal of Grey System,1995,7(2):97-101. |
| [24] | Shu W. A study of the dynamic measurement uncertainty[J].Acta Metrologia Sinica,2003,24:117-122. |



