在一定的飞行条件下,非线性气动弹性系统会出现极限环振荡、混沌等不稳定现象[1],这些不稳定现象对飞行器的结构安全构成了很大威胁.文献[2]对气动弹性颤振分析与控制方法进行了很好的总结.目前对非线性颤振主动控制问题的研究主要针对于多项式非线性[3, 4, 5].文献[6, 7]研究了迟滞非线性因素对二元机翼颤振特性的影响以及系统参数对颤振特性的影响.和多项式刚度非线性相比,迟滞非线性不仅含有非线性刚度,还含有非线性阻尼.当非线性气动弹性系统参数确定时,可以使用反馈线性化[8]等方法处理气动弹性颤振主动控制中的非线性问题.然而,由于气动弹性系统中非线性因素的随机性,导致非线性参数无法确定,因此就要用到自适应控制方法[3, 4].
反演自适应控制,也被称为反推自适应控制,是当前自适应控制领域中应用较多的理论之一.该方法很适合航空器与航天器的控制,尤其是转换控制[9, 10],文献[11]对反演自适应控制的发展及应用进行了详细总结.根据文献[12],反演自适应控制可以分为单控制器和双控制器的设计,其中单控制器的设计首先要引入特有形式的变量、虚拟控制函数,最终的控制器通过这一系列的虚拟控制函数以递推方式得到.但该方法需要先引入新的变量,从而得到严格满足特定形式的等效被控系统,且计算过程很繁琐.双控制器的反演自适应设计,不需引入特定形式的新变量,直接对控制系统施加控制器.双控制器的设计原理同单控制器的设计.文献[13]针对飞机提出了以飞行动力学描述的反演控制,它是对攻角、侧滑角和速度矢量滚转率的多变量控制器.该控制器能使大多数的初始值收敛到期望值.文献[14]针对高超声速飞行器的非线性特点,提出了动态神经网络调节函数反演自适应控制方法,设计了速度和高度控制器.文献[15]通过反演自适应控制方法设计的控制器解决了参数未知情况下的超机动飞行控制问题.文献[16]利用前/后缘双控制面,采用反演方法进行高阶滑模控制,消除了极限环振荡现象,实现了系统稳定.相比平常的控制方法,保留了系统鲁棒性的同时还避免了颤振现象.文献[17]将滑模控制结合反演方法,提出了一种综合的自适应非线性控制律,它解决了导弹制导建模的非线性,目标机动等存在不确定性的问题.仿真结果表明,该系统对系统的不确定性和外部扰动具有较好的鲁棒性.文献[18]依据Lyapunov稳定性理论,进行自适应反演控制.不同于传统的方法,它所提出的控制律可以抵抗输入饱和与抑制未知的干扰.反演自适应控制方法具有较好的自适应性和鲁棒性,并可以提供一种全局渐近稳定的控制律[19, 20, 21].文献[22]利用反演自适应控制方法对四旋翼无人机进行控制律的设计,并通过四旋翼进行遥控实验,验证了理论的正确性.
双控制面非线性气动弹性系统中的前后缘控制量是相互耦合的,以上文献所使用的反演自适应控制方法无法直接用于含前/后缘控制面的非线性气动弹性系统.本文针对该系统,在非线性参数未知的情况下,进行反演自适应控制律设计,完成了数值仿真验证. 1 气动弹性模型
含前/后缘控制面二元机翼的简化模型如图 1所示.4个自由度分别为:沉浮自由度h,向下为正;俯仰自由度α,机翼前缘抬头为正;后缘控制面偏转自由度β,向下为正;前缘控制面偏转自由度γ,向下为正;弹性轴到重心的距离为xαb,翼弦中点到弹性轴的距离为ab;操纵面铰链到机翼中点的距离为cb,操纵面重心到操纵面铰链的距离为xβb,其中:a和c为比例常数;b为机翼半弦长.
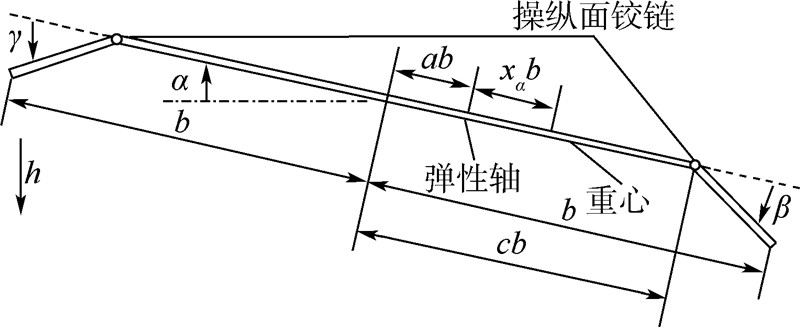 |
| 图 1 前/后缘控制面二元机翼Fig. 1 Two-dimensional airfoil with leading and trailing edge control surfaces |
如果不考虑操纵面偏转的影响,含有控制面二元机翼的动态方程则只含2个自由度,因此气动弹性动态方程可以表示为

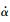 )与kα(α)分别为俯仰方向所含有的非线性阻尼与非线性刚度,二者共同组成迟滞非线性[7];L和M分别为气动力和力矩.
)与kα(α)分别为俯仰方向所含有的非线性阻尼与非线性刚度,二者共同组成迟滞非线性[7];L和M分别为气动力和力矩.
文献[5]已通过风洞试验表明可以采用准定常气动力理论描述作用在二元机翼上的气动力L和力矩M,具体表达式为
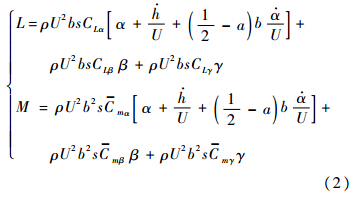
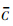 mα、
mα、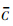 mβ和
mβ和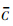 mγ分别为相应的有效力矩系数,具体关系为
mγ分别为相应的有效力矩系数,具体关系为
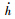
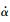 ]T,则式(1)代表的系统方程可以表示成状态空间的形式:
]T,则式(1)代表的系统方程可以表示成状态空间的形式:
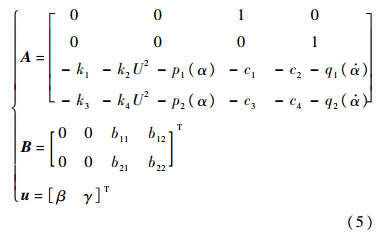

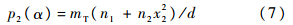
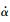 )只取一次项,令cα(
)只取一次项,令cα(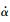 )=0.036.其他表达式参照文献[23].
2 控制律设计
)=0.036.其他表达式参照文献[23].
2 控制律设计
将状态空间式(4)所代表的被控系统写成式(8)的状态变量表达式的形式:

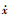 3与
3与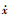 4控制项分别为(b11β+b12γ)、(b21β+b22γ),它们均是前/后缘控制面γ与β的耦合项,与经典的反演自适应控制中只有独立的控制量不同(如仅有β或是仅有γ).
4控制项分别为(b11β+b12γ)、(b21β+b22γ),它们均是前/后缘控制面γ与β的耦合项,与经典的反演自适应控制中只有独立的控制量不同(如仅有β或是仅有γ).
为解决此情况下不能直接应用反演自适应控制方法的难题,定义两个控制器,分别为u1和u2,其表达式为

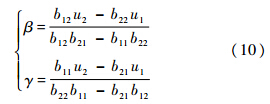
此时非线性气动弹性系统中状态方程中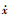 3与
3与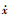 4的控制项已是独立的控制量,分别只有u1及u2单项,这时便能应用反演自适应控制方法.
4的控制项已是独立的控制量,分别只有u1及u2单项,这时便能应用反演自适应控制方法.
进行新的定义后,则被控系统变为
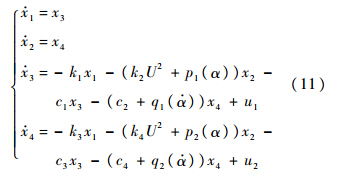
假定控制器设计过程中非线性参数是未知的,即式(6)与式(7)中的系统参数n1和n2未知.定义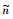 1和
1和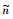 2为系统参数n1和n2的估计值,其误差为
2为系统参数n1和n2的估计值,其误差为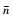 1=
1=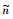 1-n1,
1-n1,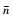 2=
2=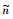 2-n2.
2-n2.
为了确定控制器,定义Lyapunov函数
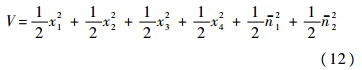

将式(11)中的各式代入式(13),并整理得
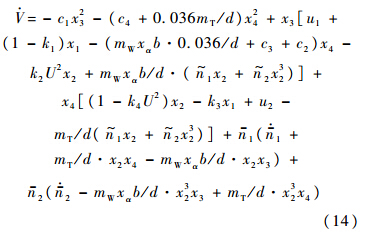
若选择控制器和参数更新变化规律分别为



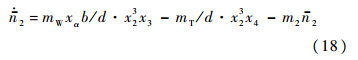

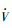 负定.
负定.
最后得到系统(x1,x2,x3,x4,n1,n2)的动力学方程:
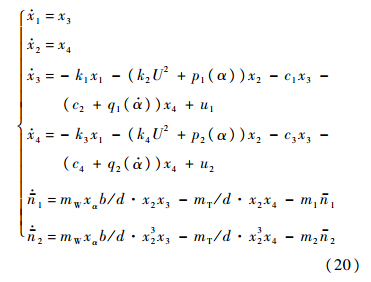
对于式(20),由于其Lyapunov函数V是正定的,其导数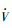 是负定的.所以,状态变量会逐渐稳定到零点.而对应的式(11)也会逐渐稳定到零点.此时的控制器u1和u2也将逐渐趋向于零.
3 结果与分析
是负定的.所以,状态变量会逐渐稳定到零点.而对应的式(11)也会逐渐稳定到零点.此时的控制器u1和u2也将逐渐趋向于零.
3 结果与分析
仿真过程中所用到的系统参数取值如下:a=-0.671 9,b=0.190 5 m,s=0.594 5 m,mW=5.230 kg,mT=15.57 kg,clα=6.757,cmα=0,kh=2 844 N/m,ch=27.43 kg/s,clγ=-0.156 6,ρ=1.225 kg/m3,cmβ=-0.671 9,Iα=0.141 9 kg·m2,xα=0.572 1,cmγ=-0.100 5,clβ=3.774.非线性模型的最高次数为3,初始条件为h(0)=0.01 m,α(0)=0.1,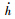 (0)=
(0)=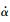 (0)=0,以上数据均引自文献[6].
(0)=0,以上数据均引自文献[6].
为计算方便,非线性参数列向量的取值与其略有不同,原文献取C=[0.03600.010]T,K=[12.7753.471 003]T,本文选取cα(<img src="PIC/20150625-α.jpg">)=0.036,K=[12.7701 003]T,即n1=12.77,n2=1 003.数值仿真中,取系统参数初始估计值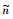 1=12,
1=12,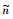 2=1 100.
2=1 100.
对于以上系统参数和初始条件,采用Runge-Kutta方法进行数值计算.由图 2的系统仿真结果可知,当来流速度U=10.49 m/s时,系统收敛;当U=10.50 m/s时,系统形成了振幅稳定的极限环振荡.由此得出,系统的颤振临界速度为10.50 m/s.与文献[23]所得到的颤振临界速度10.73 m/s相近,差别由非线性参数列向量的取值不同所导致,验证了本文计算结果的正确性.
 |
| 图 2 系统仿真结果Fig. 2 System simulation results |
取U=12 m/s,气动弹性系统的自适应控制结果如图3所示.当t<10 s时,控制输入u1=0,u2=0,即此时为开环响应,此时系统形成了振幅稳定的极限环振荡.10 s后,开始施加控制,从数值仿真结果可以看出,施加控制后不久系统稳定到零点.
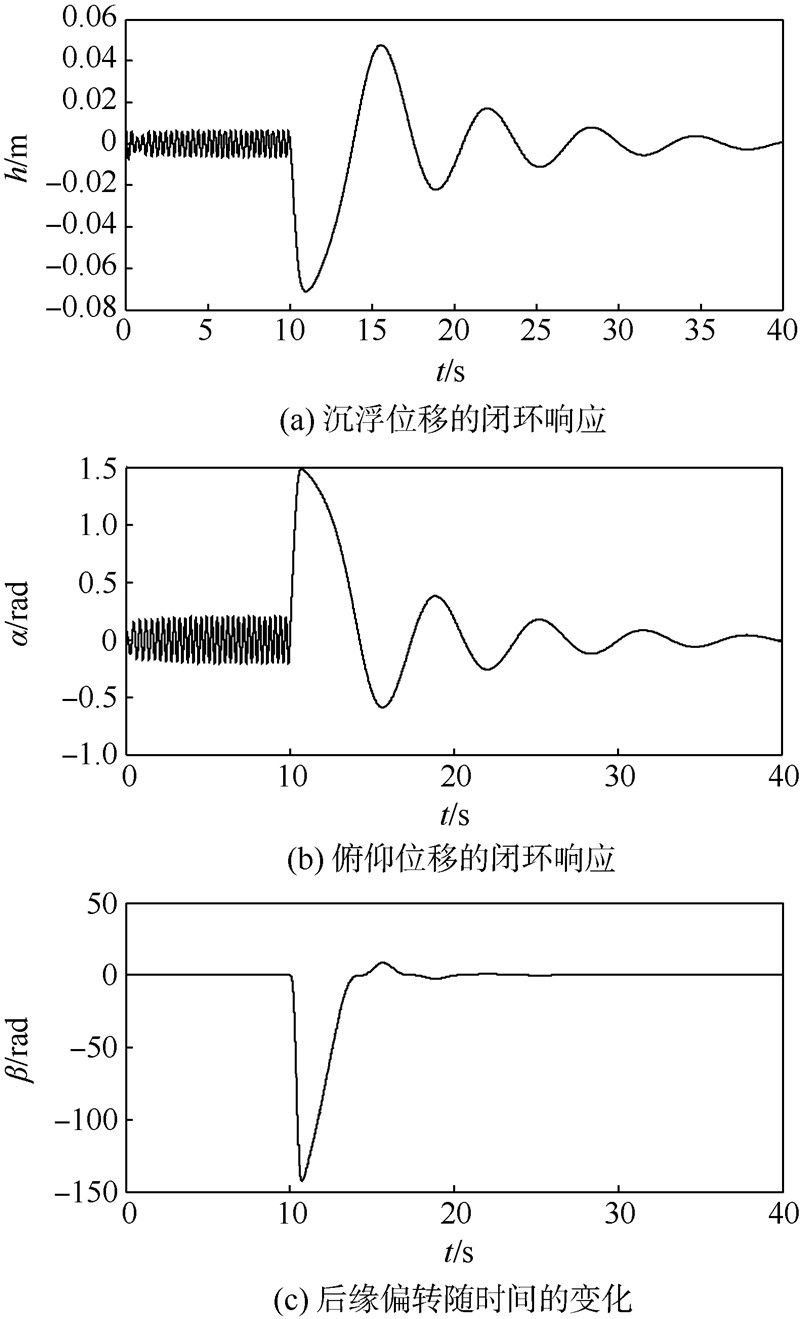 |
| 图 3 模型的自适应控制结果(U=12 m/s)Fig. 3 Model adaptive control results (U=12 m/s) |
然而,此时前后缘控制面偏转角度过大,其中后缘控制面最大偏转幅值超过130 rad.显然,此时前/后缘控制面偏转幅度远远超过实际最大偏转角度,因此需要对前/后缘控制面偏转进行限制.令前/后缘控制面最大偏转角不超过20°,重新进行仿真验证.由图 4所示的数值仿真结果可知,当限制前/后缘控制面的最大偏转后,施加控制约35 s后系统能被稳定到零点.加幅值限制后,前/后缘控制面偏转也逐渐稳定至零点.前缘控制面偏转要比后缘控制面剧烈.
 |
| 图 4 限制控制面的模型自适应控制(U=12 m/s)Fig. 4 Model adaptive control with limited control surface (U=12 m/s) |
综上可以看出,由式(11)、式(15)~式(18)所组成的闭环系统能够有效地将系统稳定到零点. 3.2 单控制面控制
为探究前/后缘对二元机翼颤振控制的贡献大小,只令其中之一工作.单后缘控制面工作时控制结果如图 5所示.
 |
| 图 5 两种情况的模型自适应控制(U=12 m/s)Fig. 5 Two different model adaptive controls (U=12 m/s) |
根据图 5,当单后缘控制面偏转时,沉浮位移和俯仰位移幅值减小的速度小于双控制面的情况.从图 5(c)也可以明显看出,单后缘控制面工作时的效率要低.两种情况都是在第10 s施加控制,当双控制面一起作用时,后缘约2 s就把幅值控制在0.1 rad以内.然而单后缘控制面工作时,在10~12 s内,后缘总是在满偏,幅值一直高于0.2 rad.
单前缘控制面工作时自适应控制结果如图 6所示,此时控制系统失效.
 |
| 图 6 限制控制面的单前缘控制系统响应(U=12 m/s)Fig. 6 Response of control system only by leading edge with limited control surface (U=12 m/s) |
由以上分析可以看出,双控制面共同作用比单一控制面的作用有效,其中单后缘控制面要比前缘控制面对系统控制更有效.
保持系统参数和初始条件不变,不断增大来流速度,发现在单后缘控制面作用下,当来流速度大于28.65 m/s时,所设计的控制律已经不能使非线性气动弹性系统达到稳定状态,此时闭环系统的响应变为极限环振荡,控制器失效.与开环颤振相比,较初始10.50 m/s的颤振速度,提高172.38%. 4 结 论
本文针对双控制面二元机翼的非线性气动弹性系统,设计了反演自适应控制律,利用Runge-Kutta数值方法对气动弹性方程进行求解,并验证了所设计控制律的有效性.数值仿真结果表明:
1) 双控制面在反演自适应控制律的作用下,可以使开环不稳定的系统稳定.
2) 仅对比单前/后缘控制面的作用,后缘控制面比前缘控制面对系统控制更有效.
3) 双控制面的共同作用比单后缘控制面的作用更快地使系统稳定.其中,单后缘控制的闭环颤振临界速度较开环颤振临界速度提高172.38%.
4) 考虑到实际情况中存在控制面偏转限制,当来流速度达到一定值时,闭环系统仍然会出现颤振现象.
| [1] | 赵永辉, 胡海岩.具有操纵间隙非线性二维翼段的气动弹性分析[J].航空学报, 2003, 24(6):521-525. Zhao Y H, Hu H Y.Aeroelastic analysis of a two dimensional airfoil with control surface freeplay nonlinearity[J].Acta Aeronautica et Astronautica Sinica, 2003, 24(6):521-525(in Chinese). |
| Cited By in Cnki (30) | Click to display the text | |
| [2] | Mukho P V.Historical perspective on analysis and control of aeroelastic responses[J].Journal of Guidance, Control and Dynamics, 2003, 26(5):673-684. |
| Click to display the text | |
| [3] | Behal A, Marzocca P, Rao V M, et al.Nonlinear adaptive control of an aeroelastic two-dimensional lifting surface[J].Journal of Guidance, Control, and Dynamics, 2006, 29(2):382-390. |
| Click to display the text | |
| [4] | Lin C M, Chin W L.Adaptive decoupled fuzzy sliding-mode control of a nonlinear aeroelastic system[J].Journal of Guidance, Control, and Dynamics, 2006, 29(1):206-209. |
| Click to display the text | |
| [5] | Platanitis G, Strganac T W.Control of a nonlinear wing section using leading-and trailing-edge surfaces[J].Journal of Guidance, Control, and Dynamics, 2004, 27(1):52-58. |
| Click to display the text | |
| [6] | 李道春, 向锦武.迟滞非线性二元机翼颤振特性分析[J].航空学报, 2007, 28(3):600-604. Li D C, Xiang J W.Aeroelastic analysis of two-dimensional airfoil with hysteresis structural nonlinearity[J].Acta Aeronautica et Astronautica Sinica, 2007, 28(3):600-604(in Chinese). |
| Cited By in Cnki (16) | Click to display the text | |
| [7] | 李道春, 向锦武.间隙非线性气动弹性颤振控制[J].北京航空航天大学学报, 2007, 33(6):640-643. Li D C, Xiang J W.Flutter control of aeroelasticity with freeplay nonlinearity[J].Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(6):640-643(in Chinese). |
| Cited By in Cnki (12) | Click to display the text | |
| [8] | Kurdila A J, Akella M R.Nonlinear control methods for high-energy limit-cycle oscillations[J].Journal of Guidance, Control, and Dynamics, 2001, 24(1):185-192. |
| Click to display the text | |
| [9] | Ali I, Radice G, Kim J.Backstepping control design with actuator torque bound for spacecraft attitude maneuver[J].Journal of Guidance, Control, and Dynamics, 2010, 33(1):254-259. |
| Click to display the text | |
| [10] | Kristiansen R, Nicklasson P J, Gravdahl J T.Satellite attitude control by quaternion-based backstepping[J].IEEE Transactions on Control Systems Technology, 2009, 17(1):227-232. |
| Click to display the text | |
| [11] | 董文瀚, 孙秀霞, 林岩.反推自适应控制的发展及应用[J].控制与决策, 2006, 21(10):1081-1084. Dong W H, Sun X X, Lin Y.Adaptive backstepping control:Development and applications[J].Control and Decision, 2006, 21(10):1081-1084(in Chinese). |
| Cited By in Cnki (45) | Click to display the text | |
| [12] | 杨绍普, 曹庆杰, 张伟.非线性动力学与控制的若干理论及应用[M].北京:科学出版社, 2011:304-309. Yang S P, Cao Q J, Zhang W.Nonlinear dynamics and control:Theory and application[M].Beijing:Science Press, 2011:304-309(in Chinese). |
| [13] | Ola H, Torkel G.Vector backstepping design for flight control[C]//Proceedings of AIAA Guidance, Navigation and Control Conference and Exhibit.Reston:AIAA, 2007, 2:1107-1116. |
| Click to display the text | |
| [14] | 涂再云, 陆阿坤, 杜军, 等.高超声速飞行器动态神经网络反推自适应控制[J].航天控制, 2013, 31(4):78. Tu Z Y, Lu A K, Du J, et al.Dynamic neural network adaptive backstepping control for hypersonic aircraft[J].Aerospace Control, 2013, 31(4):78(in Chinese). |
| Click to display the text | |
| [15] | 董文瀚, 孙秀霞, 林岩.超机动飞行的非线性反推自适应控制[J].飞行力学, 2007, 25(2):39. Dong W H, Sun X X, Lin Y.Nonlinear backstepping adaptive control of supermanuverable flight[J].Flight Dynamics, 2007, 25(2):39(in Chinese). |
| Cited By in Cnki (10) | Click to display the text | |
| [16] | Chen C L, Peng C C, Yau H T.High-order sliding mode controller with backstepping design for aeroelastic systems[J].Communications in Nonlinear Science and Numerical Simulation, 2012, 17(4):1813-1823. |
| Click to display the text | |
| [17] | Ran M P, Wang Q, Hou D L, et al.Backstepping design of missile guidance and control based on adaptive fuzzy sliding mode control[J].Chinese Journal of Aeronautics, 2014, 27(3):634-642. |
| Click to display the text | |
| [18] | Li M D, Jing W X, Macdonald M, et al.Adaptive backstepping control for optimal descent with embedded autonomy[J].Aerospace Science and Technology, 2011, 15(7):589-594. |
| Click to display the text | |
| [19] | Wu X Q, Lu J A.Adaptive control of uncertain Lü system[J].Chaos, Solitons and Fractals, 2004, 22(2):375-381. |
| Click to display the text | |
| [20] | Gao S S, Zhong Y M, Li W.Robust adaptive control for a class of chaotic system using backstepping[J].Aerospace Science and Technology, 2011, 15(6):425-430. |
| Click to display the text | |
| [21] | Peng C C, Chen C L.Robust chaotic control of Lorenz system by backstepping design[J].Chaos, Solitons and Fractals, 2008, 37(2):598-608. |
| Cited By in Cnki (0) | Click to display the text | |
| [22] | Ha C S, Zuo Z Y, Choi F B, et al.Passivity-based adaptive backstepping control of quadrotor-type UAVs[J].Robotics and Autonomous Systems, 2014, 62(9):1305-1315. |
| Click to display the text | |
| [23] | 李道春, 向锦武.非线性气动弹性模型参考自适应控制[J].航空学报, 2008, 29(2):280-283. Li D C, Xiang J W.Model reference adaptive control of nonlinearity aeroelasticity[J].Acta Aeronautica et Astronautica Sinica, 2008, 29(2):280-283(in Chinese). |
| Cited By in Cnki (1) | Click to display the text |





