2. 核工业北京地质研究院环境工程研究所, 北京 100029
2. Division of Environment Engineering, Beijing Research Institute of Uranium Geology, Beijing 100029, China
随着核工业的迅速发展,高放废物处置已逐渐成为影响环境保护和核工业持续发展的战略性课题。目前国际社会普遍认为可采用“深地质填埋法”的处置方案,即将高放废物埋藏于距离地表 500~1 000 m深的稳定地质体[1]中,并通过设置各种人工屏障来阻止核素迁移与泄漏,使之可以长期与人类的生存环境隔离,达到安全处置的目的。
国内的深地质处置库模型基于“多重屏障体系”概念,分为人工屏障和天然屏障。高放废物处置罐和缓冲/回填材料称为人工屏障,人工屏障周围的岩体则称为天然屏障。缓冲/回填材料填充于围岩与废物罐之间,是高放废物处置库长期安全性和稳定性的重要保障,应具有合适的力学性能。中国研究机构经过大量的对比研究,并在综合考虑交通条件、矿物储量等因素后,选定内蒙古高庙子(GMZ)膨润土矿床作为中国缓冲/回填材料供给矿床[1]。
GMZ膨润土的主要特点是遇水会产生大量膨胀,而在约束情况下会产生很大的膨胀力。为了合理设计高放废物处置库,需正确判定缓冲材料的膨胀性能,其中膨胀力[2]是膨润土膨胀性能研究的重要内容。本文基于超固结非饱和土本构模型及室内膨润土的膨胀力试验,建立了可考虑膨胀效应的统一硬化(UH)模型,并对高压实GMZ膨润土的膨胀特性进行了探讨。 1 考虑膨润土膨胀效应的UH模型 1.1 膨润土的膨胀机理
普通非饱和土在湿化作用下,孔隙体积逐渐减小,土体结构软化并出现垮塌[3],从而产生收缩变形,如图 1所示。而对于非饱和膨润土,一般认为其在湿化作用下产生的变形由两部分组成:一部分与普通非饱和土类似,在湿化作用下土体结构产生软化,出现收缩变形;另一部分是膨润土特殊的吸水膨胀变形,即土体团粒在湿化作用下会产生结构性变化(见图 2),不仅自身吸水产生大量膨胀,也会造成膨润土中的孔隙体积的变化,这部分变形作用在宏观上表现为膨胀变形。而最终非饱和膨润土在湿化作用下产生膨胀还是收缩变形,则取决于这两部分的变形总量:若土体团粒的膨胀变形量比土体产生的收缩变形量大,则膨润土在湿化作用下表现为膨胀变形;反之,则表现为收缩变形。
 |
| 图 1 普通非饱和土湿化机理Fig. 1 Common wetting mechanism of unsaturated soils |
 |
| 图 2 非饱和膨润土的湿化机理Fig. 2 Wetting mechanism of unsaturated bentonite |
超固结非饱和土模型(非饱和土UH模型)在当前屈服面的基础上引入参考屈服面,以反映历史应力水平[4, 5]。当前屈服面是当前应力点所在的屈服面,以H为硬化参数,参考屈服面是代表历史最大应力状态所对应的屈服面,以塑性体应变εvp为硬化参数[6, 7]。
1.2.2 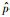 -q空间的弹塑性应变增量
-q空间的弹塑性应变增量
1) 弹性应变增量
非饱和土UH模型的弹性体应变εve增量由外力εvpe增量和吸力εvse增量共同产生:
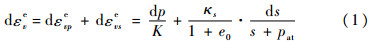
式中:s为吸力;p为饱和状态时当前应力点处的平均主应力;K为体积模量;κs为吸力变化弹性刚度系数;e0为初始孔隙比;pat为大气压力值。
弹性剪应变增量εde仅由外力产生:

式中:q为当前应力点处的广义剪应力;G为剪切模量。
2) 塑性应变增量
塑性应变受外力和吸力共同影响。塑性体应变增量为
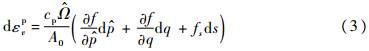
式中: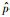 =p+ps为非饱和土当前应力点处的平均主应力,ps=ks为吸力对土体凝聚力的贡献,k为吸力对土体凝聚力贡献系数;cp=(λ(0)-κ)/(1+e0),κ为饱和土回弹线系数,λ(0)为饱和土的压缩线系数;
=p+ps为非饱和土当前应力点处的平均主应力,ps=ks为吸力对土体凝聚力的贡献,k为吸力对土体凝聚力贡献系数;cp=(λ(0)-κ)/(1+e0),κ为饱和土回弹线系数,λ(0)为饱和土的压缩线系数;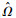 =(M4-
=(M4-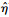 4)/(
4)/(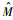 f4-
f4-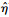 4),
4),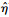 为土体某一状态下的应力比,Mf为土体的潜在强度;f=ln(
为土体某一状态下的应力比,Mf为土体的潜在强度;f=ln( /
/ x)+ln[1+q2/(M2
x)+ln[1+q2/(M2  2)]=0为超固结非饱和土UH模型屈服面,
2)]=0为超固结非饱和土UH模型屈服面, x=px+ps为吸力s时该点处的平均初始主应力,M为特征状态或临界状态应力比。
x=px+ps为吸力s时该点处的平均初始主应力,M为特征状态或临界状态应力比。

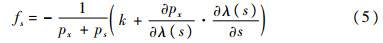
其中:λ(s)=λ(0)[(1-r)exp(-βs)+r]为吸力为s时的非饱和土压缩线系数,r和β为材料参数;px*为当前LC屈服线(当前屈服面与p-s平面的交线)与p轴的交点。
塑性剪应变增量为
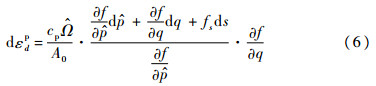
根据第1.1节的机理分析可知,膨润土中土体团粒的吸水膨胀作用将可能使膨润土产生较大的膨胀变形。基于非饱和土本构模型的塑性体应变公式,仿照普通非饱和土吸力影响因子fs式(5)构造土体团粒的吸水膨胀项gs,则假定非饱和膨润土在湿化作用下产生的塑性体应变增量为

式中:gs为膨润土土体团粒的吸力影响因子。研究GMZ膨润土的压实膨胀特性发现,膨润土的膨胀性能与土样的压实密度密切相关。刘月妙等[8]采用不同方法进行膨润土的膨胀力试验和膨胀变形试验,发现试样干密度越大,最终产生的膨胀力和膨胀变形越大,且土样膨胀特性均与其干密度呈指数函数关系。再者,在fs中考虑了当前应力状态px和吸力系数k的影响,同样地,认为这2个因素也会对膨润土的膨胀性能产生影响,且k与膨润土中土体团粒的膨胀作用呈正相关,而px与其呈负相关。根据膨润土的膨胀力试验结果进行归纳,最终确定膨润土的膨胀特性与k的3次方成正比,与当前应力状态表征量px的平方成反比。
以上述分析为依据,仿照普通非饱和土塑性体应变的吸力影响因子fs公式,构造出gs的公式:

式中:ρd为土样的初始干密度;为了平衡量纲将pat和ρw引入式(8),ρw为水的密度;α为膨润土的膨胀效应经验参数,它是衡量膨润土膨胀能力的参量,取值范围为(-π/2~π/2),可根据恒体积膨胀力试验试算得到。不同膨润土的α值不同,要特别说明的是,当α取-π/2时,tanα趋于负无穷大,则不考虑土体团粒的膨胀作用,本构模型退化为普通非饱和土本构模型;当α取π/2时,tanα趋于正无穷大,则说明膨润土中土体团粒的膨胀作用极大。
由式(7)和式(8)可知,土体团粒吸水产生的塑性膨胀应变增量可表示为

 -q空间的弹塑性应变增量
-q空间的弹塑性应变增量
在普通非饱和土UH模型的基础上,考虑土体团粒的吸水膨胀变形作用,建立了考虑非饱和膨润土膨胀效应的UH模型,该模型参数可通过常规试验获得。
考虑膨胀效应的UH模型中的弹性应变增量仍按式(1)和式(2)的形式进行计算。
考虑膨润土膨胀效应的UH模型中的塑性体应变增量由2种应变增量叠加而成,如式(7)所示;而同样地,也需考虑土体团粒的膨胀效应对膨润土抗剪性能的影响,改变式(6)中的吸力影响项,如式(10)所示。
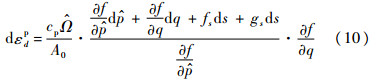
 -q空间的弹塑性本构关系
-q空间的弹塑性本构关系
非饱和膨润土湿化后在 -q空间中的总体应变εv增量和剪应变εd增量分别为
-q空间中的总体应变εv增量和剪应变εd增量分别为


将式(1)、式(2)、式(7)和式(10)代入式(11)和式(12)。经推导,可获得 -q空间中,膨润土的弹塑性应力应变的关系为
-q空间中,膨润土的弹塑性应力应变的关系为

式中:

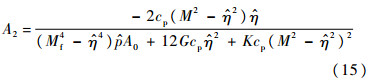
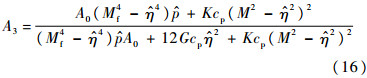

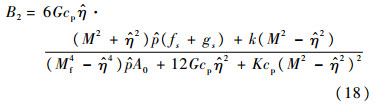
膨胀性分析采用GMZ膨润土的材料参数进行计算,其材料参数根据吸力控制下的加载试验[9]和室内非饱和压缩试验数据整理分析得到,如表 1所示。
| 材料参数 | 数值 |
| M | 1.0 |
| λ(0) | 0.18 |
| κ | 0.027 |
| v | 0.3 |
| r | 0.852 |
| β/kPa-1 | 0.100 4 |
| Gs | 2.65 |
| k | 0.01 |
| pc/kPa | 100 |
| pat/kPa | 100 |
| 注:v—土的泊松比;Gs—土粒比重;pc—参考应力。 | |
考虑膨胀效应的UH模型在土体团粒的湿化变形增量中引入了一个参数α,当α取-π/2时,不考虑土体团粒的膨胀作用;而当α取(-π/2,π/2)区间内的某值时,由考虚膨胀效应的UH模型计算的膨润土吸水会产生不同程度的膨胀作用,所以α可以代表不同膨润土的膨胀能力。对参数取不同值时的比较结果如图 3所示,α越大,代表膨润土的膨胀能力越强。
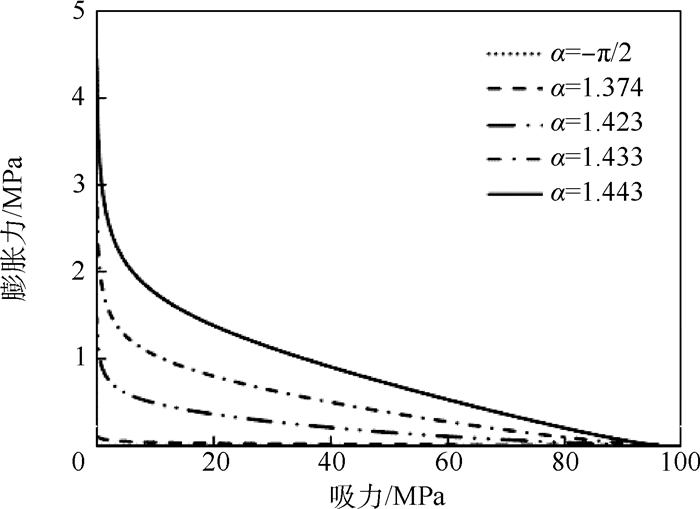 |
| 图 3 模型参数α的影响分析Fig. 3 Impact analysis of model parameter α |
本小节中采用的GMZ膨润土的初始干密度为1.5g/cm3,其他材料参数仍如表 1所示。普通非饱和土的材料参数依据姚仰平等[4]的材料分析确定,如表 2所示。此外,认为GMZ膨润土的参数α取1.443;而对于普通非饱和土,参数α取-π/2。
土样的初始净应力均为310kPa,保持吸力不变分别按表 3中的加载路径进行等p加载,当应力比为0.9时湿化至饱和,再等p加载至破坏。
| 材料参数 | 数值 |
| M | 1.0 |
| λ(0) | 0.2 |
| κ | 0.02 |
| v | 0.3 |
| r | 0.75 |
| β/kPa-1 | 0.0125 |
| Gs | 2.65 |
| k | 0.6 |
| pc/kPa | 100 |
| pat/kPa | 100 |
| α | -π/2 |
| 土样 | 前期 固结 压力/ kPa | 初始 应力/ kPa | 初始 超固结 参数 | 初始 吸力/ kPa | 加载至 应力比 | 湿化至 吸力/ kPa |
| GMZ 膨润土 | 16 448 | 310 | 0.035 | 96 000 | 0.9 | 0 |
在不同的前期固结压力下,分别按非饱和土UH模型和考虑膨胀效应的UH模型进行膨润土的三轴预测,结果如图 4和图 5所示。
从计算结果可以看出,前期固结压力对膨润土的应力应变关系影响很大。当不考虑土体团粒的膨胀作用时(见图 4,ε1为主应变),若前期固结压力很大,由于GMZ膨润土特殊的材料特性和较大的初始超固结程度,其在湿化路径下会产生弹性膨胀变形;而若土体的前期固结压力较小,土体则会产生较大的收缩变形。当考虑土体团粒的膨胀作用时(见图 5),不同的前期固结压力会使土体产生不同程度的膨胀作用,前期固结压力越大,则土体的初始干密度越大,作为其在湿化作用下产生的膨胀量就越大,模型预测合理。
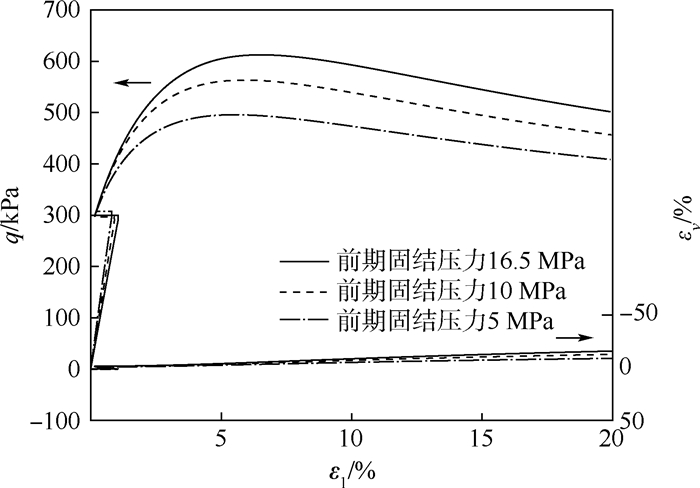 |
| q-当前应力点处的广义剪应力;ε1-主应变. 图 4 加载—湿化—再加载路径下的应力应变曲线1Fig. 4 Stress-strain curves of loading-wetting-reloading path 1 |
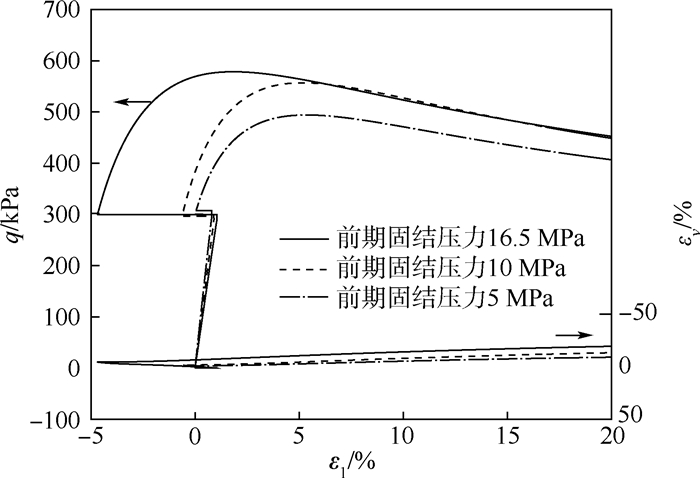 |
| 图 5 加载—湿化—再加载路径下的应力应变曲线2Fig. 5 Stress-strain curves of loading-wetting-reloading path 2 |
叶为民等[10]利用UPC固结仪,对初始吸力为96MPa的高压实GMZ膨润土进行了湿化试验,测量其在侧限条件下产生的膨胀力。对不同干密度条件下的试验数据进行整理,如图 6所示。基于考虑膨胀效应的UH模型,利用表 1中的材料参数进行相同条件下的膨胀力试验计算,计算结果也如图 6所示。可以看出,随着土样饱和度的增大,基质吸力减小,膨胀力增加,此外,干密度越大,湿化产生的膨胀力也越大。通过对比可知,模型可以较好地反映不同初始干密度的GMZ膨润土在湿化作用下的膨胀特性。
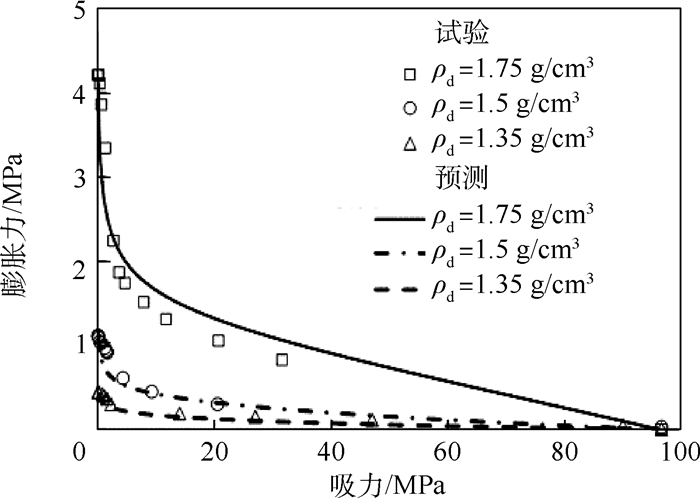 |
| 图 6 膨胀力随吸力的变化过程Fig. 6 Change processes of swelling pressure with suction |
陈正汉等[11]利用三向胀缩仪对高压实GMZ膨润土进行试验,在不同吸力条件下,将不同初始干密度的膨润土湿化,研究其膨胀力随时间的演化规律。对不同初始吸力条件下的膨胀力试验数据进行整理,如图 7所示。可以看出,在同一初始吸力条件下,干密度越大,产生的膨胀力越大。同样基于考虑膨胀效应的UH模型,采用表 1中的
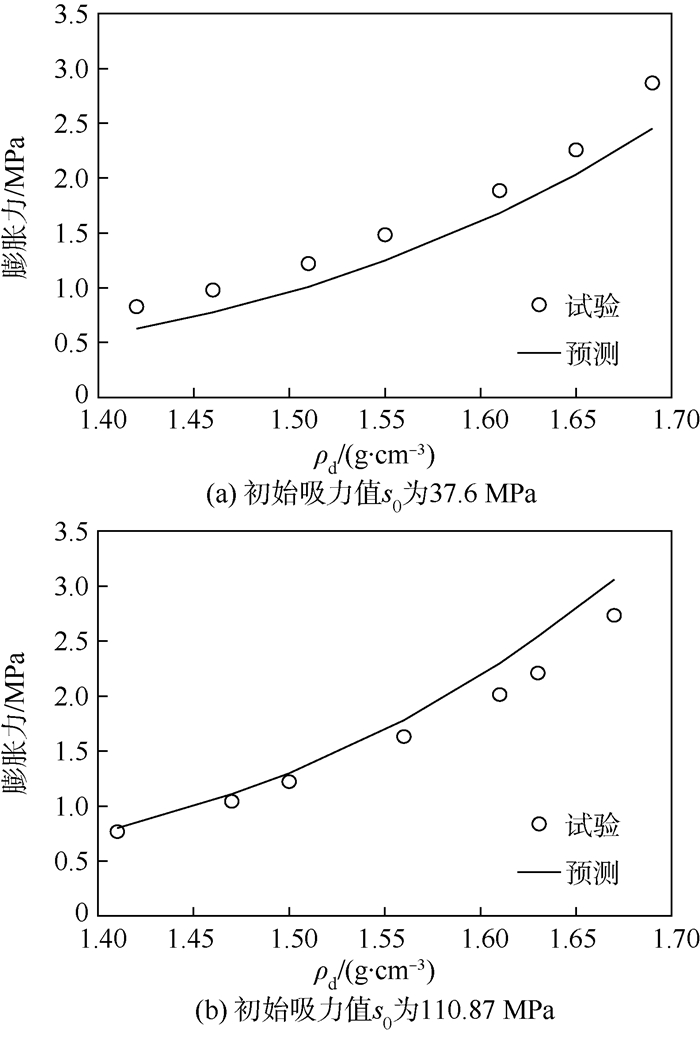 |
| 图 7 不同干密度的GMZ膨润土的膨胀力Fig. 7 Swelling pressure of GMZ bentonite under different dry densities |
材料参数进行相同条件下的膨胀力计算,计算结果如图 7所示。从对比结果可以看出,模型可很好地反映不同初始吸力和不同干密度的膨润土的膨胀规律。 3 模型的有限元实现及程序验证 3.1 模型的有限元实现
利用考虑膨胀效应的UH模型进行有限元计算是应用Newton-Raphson算法获得复杂非线性问题解的过程,而且整个计算中融合了增量和迭代的过程[12, 13]。将模型进行三维化,并基于ABAQUS有限元软件的二次开发平台,采用FORTRAN语言编制了考虑膨胀效应UH模型的用户子程序[14, 15]。程序中重点定义了吸力变量和吸力变化引起的弹性及塑性应变增量,从而实现了该模型与ABAQUS软件的结合。 3.2 程序验证 3.2.1 程序验证1——常规三轴试验
对GMZ膨润土进行三轴试验的有限元模拟。模型采用三维实体单元(C3D20R),三轴试样直径40mm,高80mm,考虑到三轴试验中试样的对称性,取1/4的土样建立模型[16],如图 8所示。边界条件为在模型对称面约束法向位移,而在模型下表面约束竖向位移。网格划分如图 8所示,共525个节点,80个单元,有限元分析中先采用应力加载,之后湿化,最后采用位移加载方式。
 |
| 图 8 常规三轴试验的有限元分析模型及网格Fig. 8 Models and meshes for finite element analysis of conventional triaxial test |
图 9为应用考虑膨胀效应UH模型对超固结程度为0.035的GMZ膨润土进行三轴压缩试验的有限元模拟,分析中膨润土的加载路径仍为等p加载—湿化—加载,材料参数如表 1所示。通过与模型预测结果的对比可知,应用考虑膨胀效应的UH模型的有限元计算结果与用该模型编制的预测程序计算结果吻合度较高,不仅可模拟超固结膨润土峰值、软化等特性,还能反映膨润土在湿化条件下会产生体积膨胀的特性,说明编制的程序可较好地反映GMZ膨润土的应力应变特性,验证了该模型子程序的正确性。
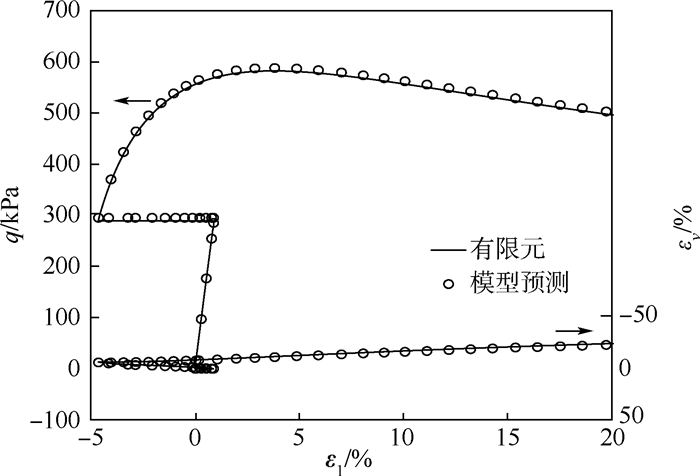 |
| 图 9 有限元计算结果与模型预测结果的比较Fig. 9 Comparison of FEM results and model forecast results |
基于叶为民等[10]开展的GMZ膨润土膨胀力试验,利用ABAQUS建立了如图 10所示的有限元模型。该模型由圆柱形GMZ膨润土及钢材料固结仪组成,以此模型可更准确地模拟膨胀力试验。膨润土试样直径为50mm,厚度为20mm,固结仪模型壁厚10mm,为空心圆柱紧包膨润土。单元类型均采用三维实体单元(C3D20R),如图 10所示,共划分了2974个节点,424个单元。计算时,假定固结仪是完全刚性的,约束其外表面的所有位移。
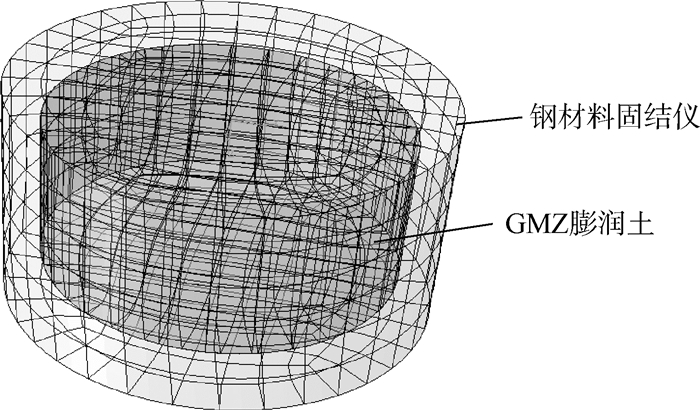 |
| 图 10 膨胀力试验的有限元模型及网格Fig. 10 Models and meshes for finite element analysis of swelling force test |
膨润土前期固结压力为500kPa,初始吸力96MPa,临界状态应力比为1.0,其他主要材料参数仍见表 1,钢制固结仪采用弹性模型进行计算,弹性模量E=1.2×105MPa。有限元分析中控制膨润土的吸力使其逐渐降为0,计算结果显示模型中各点产生的膨胀力不均匀,应力最大点位于土体环形表面中心线处,而应力最小点则位于土体的棱线处。选取膨润土表面中心点、膨胀力最大点及最小点3点的计算结果与试验数据比较,如图 11所示。从比较结果可以看出,有限元计算结果与试验数据规律一致,说明模型可较好地反映膨润土的湿化特性,再次验证了用户子程序的合理性。
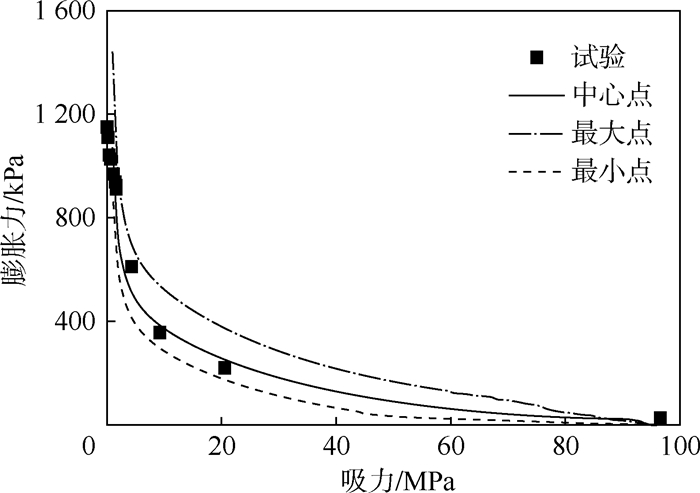 |
| 图 11 膨润土中不同点的模拟结果Fig. 11 Simulation results of different points in bentonite |
针对膨润土在湿化路径下会产生大量膨胀的特性,本文在超固结非饱和土UH模型的基础上,提出了考虑膨胀效应的UH模型,并借助有限元软件进行了模型的有限元实现。综合全文,可得:
1) 基于膨润土的湿化膨胀机理,仿照非饱和土UH模型中的吸力影响因子fs构造了膨润土土体团粒的吸水膨胀项,从而提出了考虑膨胀效应的UH模型。该模型只比非饱和土UH模型增加了一个参数,不仅能够反映普通加载路径下膨润土的应力应变特性,还能较好地反映其在湿化路径下的膨胀性能。
2) 基于有限元软件的二次开发平台,利用FORTRAN语言编制了模型的用户子程序,并通过对常规三轴试验和膨胀力试验的有限元模拟,验证了子程序的正确性及合理性,为进一步的工程分析奠定了基础。
| [1] | 王驹,陈伟明,苏锐,等.高放废物地质处置及其若干关键科学问题[J].岩石力学与工程学报,2006,25(4):801-812. WANG J,CHEN W M,SU R,et al.Geological disposal of high-level radioactive waste and its key scientific issues[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(4):801-812(in Chinese). |
| Cited By in Cnki (100) | |
| [2] | 马利科,刘月妙,曹胜飞.高庙子膨润土膨胀力影响因素研究[C]//第三届废物地下处置学术研讨会论文集.北京:中国原子能出版社,2010:423-429. MA L K,LIU Y M,CAO S F.Studies on the influence factors of GMZ bentonite's swelling pressure[C]//The Third Academic Seminar on Underground Waste Disposal.Beijing:China Atomic Energy Press,2010:423-429(in Chinese). |
| Cited By in Cnki (2) | |
| [3] | 姚仰平,周安楠,侯伟.砂土硬化特征的描述及其试验验证[J].北京航空航天大学学报,2006,32(10):1186-1192. YAO Y P,ZHOU A N,HOU W.Description of hardening characteristics of sand and its confirmation[J].Journal of Beijing University of Aeronautics and Astronautics,2006,32(10):1186-1192(in Chinese). |
| Cited By in Cnki | |
| [4] | 姚仰平,牛雷,崔文杰,等.超固结非饱和土的本构关系[J].岩土工程学报,2011,33(6):834-839. YAO Y P,NIU L,CUI W J,et al.UH model for unsaturated soils[J].Chinese Journal of Geotechnical Engineering,2011,33(6):834-839(in Chinese). |
| Cited By in Cnki (5) | |
| [5] | 罗汀,郭敏.K0固结黏土的渐近状态模拟[J].工业建筑,2011,41(9):35-37. LUO T,GUO M.Asymptotic state modelling for K0 consolidated clay[J].Industrial Construction,2011,41(9):35-37(in Chinese). |
| Cited By in Cnki | |
| [6] | 罗汀,田新国.考虑土渐进状态特性的应力应变关系[J].北京航空航天大学学报,2010,36(3):315-332. LUO T,TIAN X G.Stress-strain in incremental law in asymptotic state for soils[J].Journal of Beijing University of Aeronautics and Astronautics,2010,36(3):315-332(in Chinese). |
| Cited By in Cnki | |
| [7] | 侯伟,姚仰平.统一硬化模型在复杂加载条件下的应用[J].北京航空航天大学学报,2008,34(9):1105-1108. HOU W,YAO Y P.Application of unified hardening model under complex loading[J].Journal of Beijing University of Aeronautics and Astronautics,2008,34(9):1105-1108(in Chinese). |
| Cited By in Cnki | |
| [8] | 刘月妙,王驹,谢敬礼,等.微机控制高温高压膨胀渗透仪的研制和应用[C]//第四届废物地下处置学术研讨会论文集.北京:中国原子能出版社,2012:73-78. LIU Y M,WANG J,XIE J L,et al.High temperature and high pressure apparatus for swelling pressure and permeability of buffer material and its application[C]//The Forth Academic Eeminar on Underground Waste Disposal.Beijing:China Atomic Energy Press,2012:73-78(in Chinese). |
| Cited By in Cnki | |
| [9] | CUI Y J,TANG A M,QIAN L X,et al.Thermal-mechanical behavior of compacted GMZ bentonite[J].Soils and Foundation,2011,51(6):1065-1074. |
| Click to display the text | |
| [10] | 叶为民,SCHANZ T,钱丽鑫,等.高压实高庙子膨润土GMZ01的膨胀力特征[J].岩石力学与工程学报,2007,26(S2):3861-3865. YE W M,SCHANZ T,QIAN L X,et al.Characteristics of swelling pressure of densely compacted Gaomiaozi bentonite GMZ01[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(S2):3861-3865(in Chinese). |
| Cited By in Cnki (23) | |
| [11] | 秦冰,陈正汉,刘月妙,等.高庙子膨润土GMZ001三向膨胀力特性研究[J].岩土工程学报,2009,31(5):756-763. QIN B,CHEN Z H,LIU Y M,et al.Characteristics of 3D swelling pressure of GMZ001 bentonite[J].Chinese Journal of Geotechnical Engineering,2009,31(5):756-763(in Chinese). |
| Cited By in Cnki (10) | |
| [12] | 王乃东,姚仰平.广义非线性强度与广义滑动面[J].北京航空航天大学学报,2011,37(1):101-105. WANG N D,YAO Y P.Generalized nonlinear strength and general mobilized plane[J].Journal of Beijing University of Aeronautics and Astronautics,2011,37(1):101-105 (in Chinese). |
| Cited By in Cnki | |
| [13] | 罗汀,张盼盼,姚仰平,等.超固结非饱和土UH模型的有限元实现[J].世界核地质科学,2014,31(S1):322-326. LUO T,ZHANG P P,YAO Y P,et al.Finite element realization of the UH model for unsaturated soils[J].World Nuclear Geoscience,2014,31(S1):322-326(in Chinese). |
| Cited By in Cnki (5) | |
| [14] | YAO Y P,HOU W,ZHOU A N.UH model:Three-dimensional unified hardening model for overconsolidated clays[J].Geotechnique,2009,59(5):451-469. |
| Click to display the text | |
| [15] | 罗汀,秦振华,姚仰平,等.UH模型切线刚度矩阵对称化及其应用[J].力学学报,2011,43(6):1186-1190. LUO T,QIN Z H,YAO Y P,et al.Symmetrization and application of tangent stiffness matrix for UH model[J].Chinese Journal of Theoretical and Applied Mechanics,2011,43(6):1186-1190(in Chinese). |
| Cited By in Cnki (7) | |
| [16] | 姚仰平,冯兴,黄祥,等.UH模型在有限元分析中的应用[J].岩土力学,2010,31(1):237-245. YAO Y P,FENG X,HUANG X,et al.Application of UH model to finite element analysis[J].Rock and Soil Mechanics,2010,31(1):237-245(in Chinese). |
| Cited By in Cnki (12) |



