2. 流体动力与机电系统国家重点实验室, 杭州 310027
2. State Key Laboratory of Fluid Power Transmission and Control, Hangzhou 310027, China
弹跳机器人可以越过数倍于自身尺寸高度的障碍物,较传统地面移动机器人,如轮式、履带式和腿式机器人等,具有很强的越障能力和未知地形适应性[1]。
弹跳机器人野外工作时,通常需要携带相应的负载,如摄像头、传感器和机械手等进行相关活动,因此需要增强机器人的带负载能力。带负载能力的增加需要弹跳机器人具有更大的瞬时功率,由于起跳时机器人与地面间的作用时间非常短,因此会产生更大的相互作用力。目前研究的弹跳机器人多数是由电机驱动或智能材料驱动(如仿袋鼠弹跳机器人[2]、MSU Jumper[3]、EPFL Jumper[4]、Grillo Ш[5]、MIT microbot[6]和Flea robot[7]),该类机器人质量较轻,起跳过程中对地作用力较小,并且为保持机器人平衡通常设计较大接触面积的脚,因而对地面压力较小,地面对其弹跳性能影响较小。
燃气动力弹跳机器人满足弹跳机器人瞬时大功率的驱动要求,文献[8]通过比较显示燃气动力弹跳机器人具有较高的带负载能力。弹跳机器人带负载能力的增强对地面会产生更大的作用力,因此地面的力学特性会直接影响机器人的弹跳性能:刚性地面变形小,弹跳机器人脚几乎不会下陷;泥土地面受到作用力时会产生较大下陷深度,影响了机器人的起跳速度。为提高弹跳机器人的弹跳和带负载能力,一方面需要优化机器人结构以减轻其质量,另一方面需要研究不同力学特性地面对其弹跳性能的影响。美国Sandia国家实验室较早地开展了燃气动力弹跳机器人的研究[9],之后Boston动力实验室对其性能进行提高,研制了弹跳高度1~8 m的SandFlea弹跳机器人[10],但其仍选择刚性地面进行弹跳试验。相比于轮式[11-12]、履带式[13]和腿式移动机器人[14],弹跳移动机器人在不同地面的弹跳运动性能研究相对较少。
本文旨在分析燃气动力弹跳机器人在不同力学特性地面的弹跳性能,为弹跳机器人在不同地面弹跳能源气体输入控制及特定地点越障高度分析提供依据。
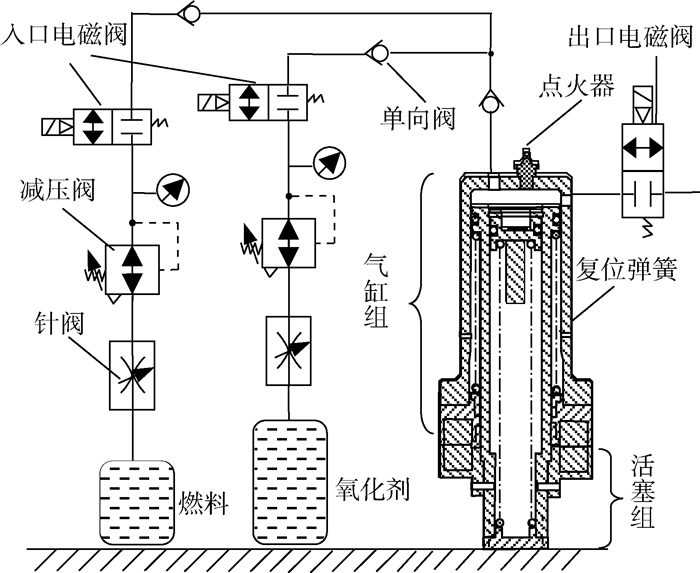
1 起跳原理 1.1 结构组成弹跳机器人三维模型与样机如图 1所示,包括:机器人载体与弹跳驱动系统。载体包括车体、减震车轮及支撑腿。车体一方面用于承载,另一方面用于保护机器人相关部件。减震车轮用于减小机器人落地时的冲击力。支撑腿用于调整机器人起跳角度。弹跳驱动系统是弹跳的动力系统,是将气体燃烧释放的热能转化为机械能的装置,其结构示意图如图 2所示,包括弹跳驱动器和气路装置[15]。弹跳驱动器是弹跳机器人的关键部件,其结构包括气缸—活塞组件、锁紧机构及点火器。锁紧机构的锁紧力是通过气缸组与活塞组之间的磁铁吸力实现的。气路装置包括气源、针阀、调压阀、电磁阀、单向阀,能源气体为燃料——丙烷(99.9%)、氧化剂——一氧化二氮(>99%),它们都具有经济、无毒、常温稳定、反应温和及易于存放等优点[16],并且一氧化二氮自身分解,释放能量,有利于提高弹跳性能。弹跳驱动器的主要参数:行程48 mm、缸体内径37 mm、气缸组质量0.39 kg、活塞杆组质量0.35 kg。

|
| 图 1 弹跳机器人三维模型与样机图 Fig. 1 Pictures of hopping robot 3D model and prototype |
|
| 图 2 弹跳驱动器结构示意图 Fig. 2 Schematic diagram of hopping actuator |
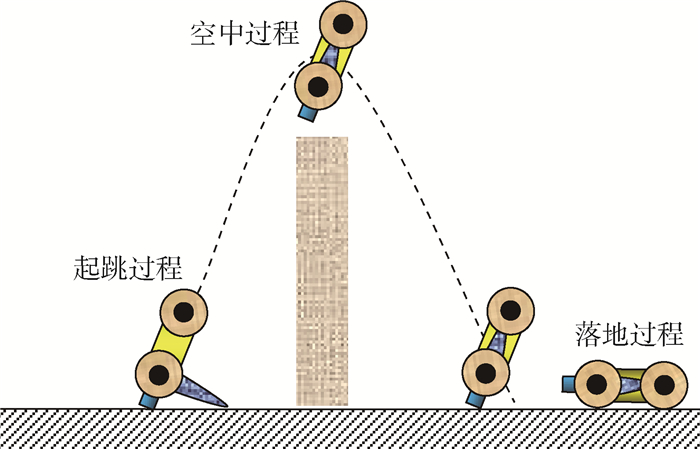
弹跳机器人弹跳过程如图 3所示,具体如下:
|
| 图 3 机器人弹跳过程示意图 Fig. 3 Schematic diagram of robot hopping process |
1) 起跳过程。①根据地面特点及障碍物的高度与形状,选择弹跳地点并调整弹跳角度;②打开针阀,调节减压阀到所需压力,然后打开入口电磁阀分别向驱动器依次充入丙烷和一氧化二氮;③点火器点火,机器人弹跳。由于在起跳过程中机器人以活塞杆底端与地面接触,因此本文以下称活塞杆为弹跳脚。
2) 空中过程。机器人起跳后出口电磁阀打开,废气排出,活塞杆与支撑腿恢复到初始位置。
3) 落地过程。机器人从空中落下与地面产生碰撞,依靠减震车轮减小碰撞过程中地面对车体的冲击力,当机器人落地静止后,弹跳过程结束。
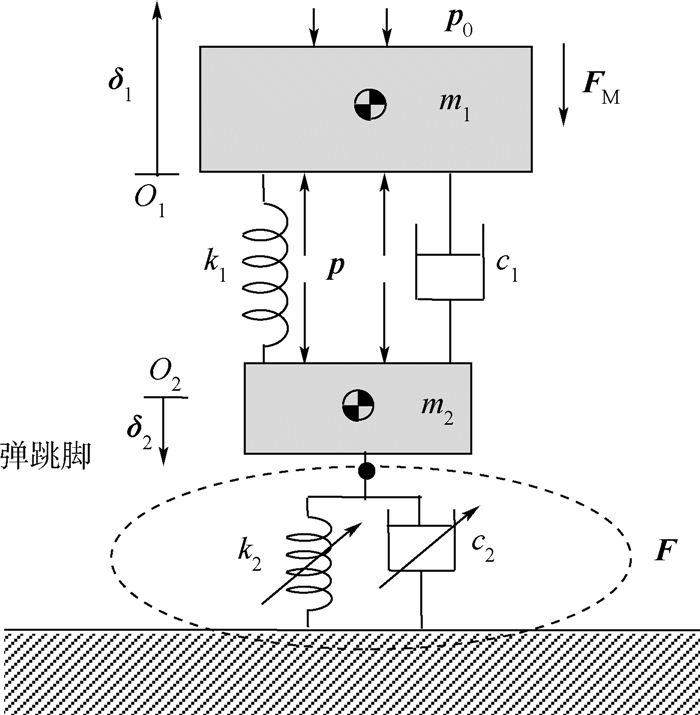
2 起跳分析 2.1 动力学模型机器人起跳过程是弹跳机器人的关键过程,在该过程中弹跳驱动器将化学反应产生的热能转化为机器人起跳动能,该过程直接体现了燃气动力弹跳机器人的弹跳性能,因此对该过程进行详细分析。为简化分析本文只研究垂直起跳条件下机器人在不同力学特性地面的弹跳性能。机器人垂直起跳过程的动力学模型可简化为图 4所示的两自由度弹簧-质量-阻尼系统,其中m1为驱动器的气缸组和机器人载体质量,m2为驱动器的活塞杆组质量,缸体与活塞之间摩擦简化为阻尼系数为c的阻尼器,脚与地面的接触简化为非线性弹簧-阻尼系统,分别对m1与m2进行分析。
|
| k1—复位弹簧弹性系数;k2—脚与地面接触简化弹性元件的刚度系数;c1,c2—阻尼系数;p—燃烧室内气体压力;p0—当地大气压力;δ1—m1上升位移;δ2—弹跳脚下陷位移;FM—磁铁锁紧力;F—脚与地面之间的作用力;O1,O2—m1和m2初始位置。 图 4 机器人脚与地面接触模型 Fig. 4 Robot foot and ground contact model |
对m1进行受力分析,则其动力学方程可表示为
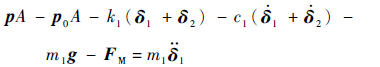 (1)
(1)
式中:A为缸体内腔面积;g为当地重力加速度。
对m2受力分析,其动力学方程可表示为
 (2)
(2)
由于燃烧室内气体反应速度极快,压力变化过程可分为等容燃烧与绝热膨胀2个过程,因此燃烧室内压力可表示为
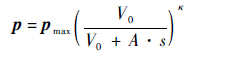 (3)
(3)
式中:pmax为等容燃烧达到平衡时的压力;V0为燃烧室的初始体积;κ为燃烧室内气体绝热系数(取为1.33);s为m1与弹跳脚之间相对位移,可表示为
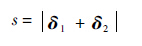 (4)
(4)
当m1与弹跳脚之间相对位移达到驱动器的最大行程时发生碰撞,以共同速度v起跳,可由式(2)-式(1)并积分得到,其表达式为
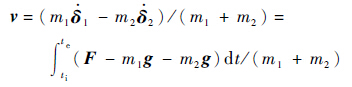 (5)
(5)
式中:ti为燃烧初始时刻;te为碰撞时刻。式(5)显示根据弹跳脚与地面之间的接触力可以得到机器人的起跳速度。起跳过程中单位质量的脚与地面的作用力冲量越大,机器人起跳速度越大,因此机器人获得的弹跳动能也越大。
根据能量守恒定律,机器人最终的弹跳高度可表示为
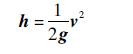 (6)
(6)
弹跳脚的相关特征及参数:材料2A12、形状为圆形、底部直径26 mm。由于脚在起跳过程中变形量很小,将其视为刚性脚,则弹跳脚与地面接触分为2种情况:刚性脚VS刚性地面、刚性脚VS软地面。
1) 若地面为刚性地面,则起跳过程中弹跳脚始终处于静止状态,该系统为单自由度系统,式(2)中δ2=0,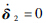
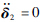
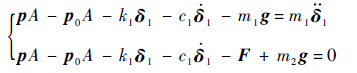 (7)
(7)
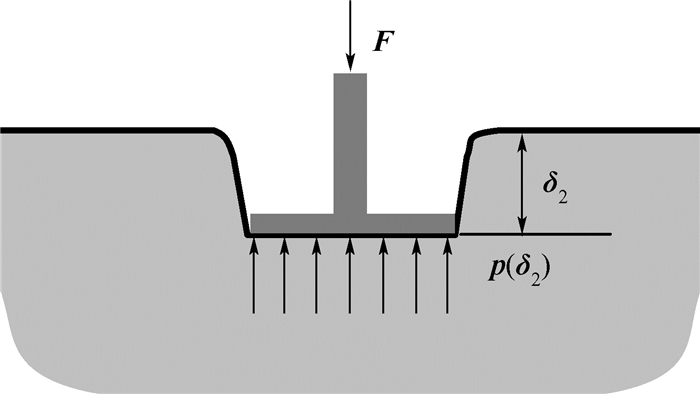
2) 若地面为松软地面,脚与地面接触过程土壤应力分布如图 5所示。目前机器人与地面接触力计算主要是基于Bekker理论模型[17],根据该模型得到接触应力与下陷深度的关系,其表达式为
|
| 图 5 脚与地面接触应力分布 Fig. 5 Stress distribution between foot and ground |
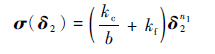 (8)
(8)
式中:kc为黏性模量;kf为摩擦模量;n1为下陷深度指数;b为脚与地面的接触尺寸。
根据接触应力表达式,则脚与地面之间作用力大小可表示为
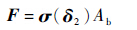 (9)
(9)
式中:σ为脚与地面接触应力;Ab为脚与地面接触面积。
由Bekker模型得到接触力表达式简单,但该模型不含下陷速度对接触力的影响,因此本文选用Hunt-Crossley接触力模型对弹跳脚与地面作用力进行分析[18],其表达式为
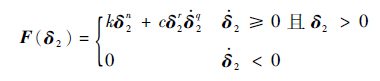 (10)
(10)
式中:n为刚度指数;r为阻尼项下陷深度指数;q为阻尼项下陷速度指数。其中k、n项为准静态参数,即与速度无关项,其余参数为动态项参数。
Wong[19]得到典型地面的下陷深度与接触应力相关参数,则利用Bekker模型参数可以得到Hunt-Crossly模型中的准静态项参数。对于动态项参数,根据Ding等[20]分析方法进行脚与地面接触参数辨识。
3 接触力测试与弹跳试验 3.1 脚与土壤接触力参数辨识为研究机器人在不同地面的弹跳性能,模拟3种具有典型力学特性的地面,分别为:刚性地面、硬黏土地面及草地地面。刚性地面选用材料为2A12的厚铝板;硬黏土地面是将土颗粒碾细,放入土容器用水润湿,放置3 h待水完全浸入土中,用平整圆锭将土夯实,放于干燥环境静置2个月,培成硬黏土;草地地面是在平整草地上取整块土,将其整体放入土容器中,然后用当地土,将土容器周围填满,浇水培育置于自然环境2个月。3种不同地面实物图如图 6所示。

|
| 图 6 3种不同地面实物图 Fig. 6 Pictures of three different grounds |
为测试脚与地面接触力学参数,构建如图 7所示的测试装置,该装置由气缸(直径100 mm,行程100 mm)、气泵、三位五通电磁阀、位移传感器(量程150 mm)、力传感器、待测土和施力脚等组成。气缸用于施加作用力,气泵用于为气缸提供气源,电磁阀控制运动方向,位移传感器测试施力脚的位移,力传感器用于测试脚与土壤之间的作用力。

|
| 图 7 测试装置 Fig. 7 Test setup |
具体测试步骤如下:
1) 脚的高度调整。调整施力脚的高度,保证脚与土壤刚好接触,采集位移传感器的值为x0。
2) 数据采集。电磁阀通电使气缸处于下行状态,打开气泵缓慢加压,同时采集力与位移传感器的数据。
3) 静态参数拟合。利用最小二乘法对试验数据进行拟合,得到参数k、n,其拟合曲线如图 8所示。

|
| 图 8 准静态力-位移测试曲线及拟合曲线 Fig. 8 Quasi-static force-displacement test and fitting curves |
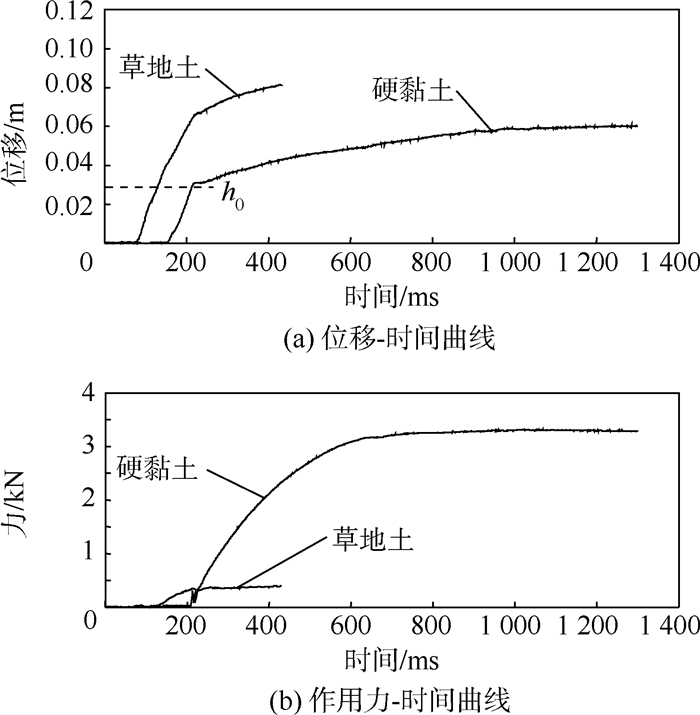
4) 动态相关参数测试。关闭电磁阀,调整气泵工作压力,脚与土之间高度为h0,当气泵压力达到设定值,打开电磁阀,脚在气缸力的作用下向下加速运动,从而保证当脚运动到土的高度,具有一定的初速度。在该过程中采集相关数据,则脚在土中下陷深度=脚的位移-h0。测得的数据如图 9所示,则脚的下陷速度可由式(11)求得
|
| 图 9 地面动态测试结果曲线 Fig. 9 Ground dynamic test result curves |
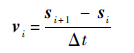 (11)
(11)
式中:vi为第i时刻的速度;si+1和si分别为第i+1时刻与第i时刻的位移;Δt为第i+1时刻与第i时刻之间的时间间隔。
试验中,当气缸推动质量为66 g的脚m3下行时,力传感器测得的力F1为模拟脚主动力,则对脚进行受力分析
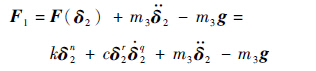 (12)
(12)
利用试验测得的数据根据式(12),对其余参数进行拟合,得到脚与土壤接触力相关参数如表 3所示。
| 名称 | k | n | c | r | q |
| 草地 | 1 213 | 0.398 | 246.229 | 0.1 | 0.635 |
| 硬黏土 | 28 090.4 | 0.71 | 232 600 | 1.219 | 0 |
3.2 仿真与试验测试
试验测试装置实物图如图 10所示,该装置主要由直线轴承、四爪卡盘和模拟弹跳脚组成。直线轴承对模拟脚起导向作用,使脚的下陷方向沿垂直方向,四爪卡盘固定直线轴承,防止弹跳过程中模拟脚发生倾倒。

|
| 图 10 试验测试装置实物图 Fig. 10 Picture of experimental test device |
由于弹跳试验主要目的在于测试不同力学特性地面对弹跳性能的影响,为了方便试验,防止机器人在模拟弹跳脚上发生倾倒,利用负载配重的3.55 kg弹跳机构进行弹跳试验,该机构如图 11所示。试验时将弹跳机构放在图 10所示的模拟脚上进行测试,主要设备有测试初始压力的传感器和爆炸压力的传感器。

|
| 图 11 弹跳机构装置 Fig. 11 Hopping mechanism assembly |
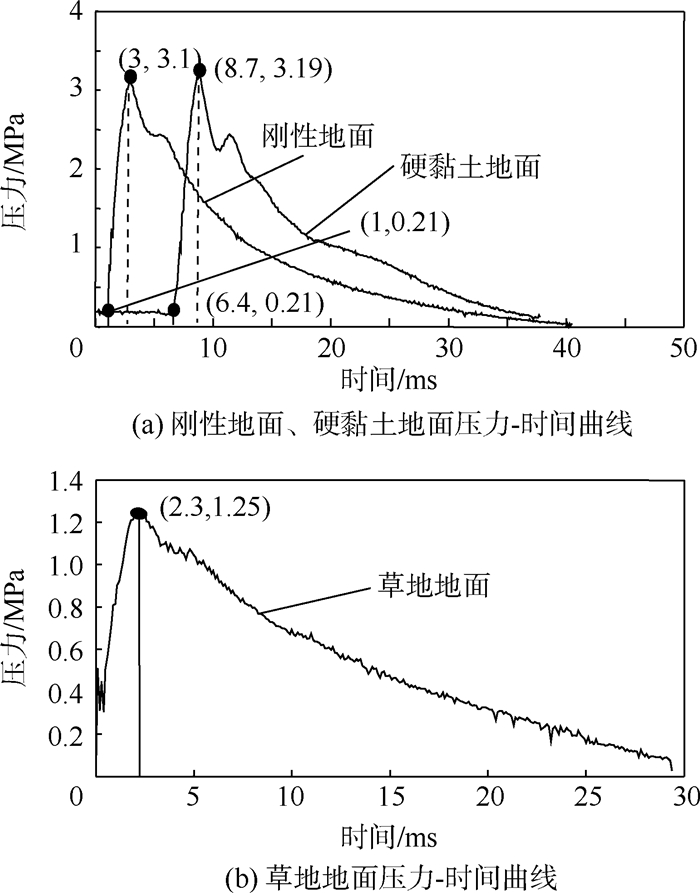
在刚性地面与硬黏土地面测试时驱动器充入相同压力的能源气体(0.01 MPa丙烷、0.21 MPa一氧化二氮)。在模拟草地地面试验中,为防止气缸与活塞杆之间的相对速度太大,导致弹跳驱动器由于碰撞能量过大而损坏,试验过程中降低燃烧室能源气体充入量,初始充入气体的压力为0 MPa,具体操作是先充入0.01 MPa丙烷和0.21 MPa一氧化二氮形成混合气体,然后打开电磁阀,当压力减小到大气压力时关闭电磁阀。弹跳机构在不同模拟地面弹跳测得燃烧室的压力变化曲线如图 12所示。从中可以看出:弹跳机构在刚性地面和硬黏土地面弹跳时的燃烧室内最大压力分别为3.1 MPa和3.19 MPa,二者相差较小,草地地面燃烧室内最大压力为1.25 MPa。刚性地面压力上升的时间为由点(1,0.21)到(3,3.1);在硬黏土地面压力上升时间间隔为(6.4,0.21)到(8.7,3.19);草地地面则从(0,0)到(2.3,1.25),则在3种地面弹跳时达到最大压力的时间分别约为2.0、2.3和2.3 ms,说明在极短时间内燃烧室内的燃烧反应达到平衡,因此先前等容燃烧假设分析是相对合理的。图 13为弹跳机构在3种地面的弹跳结果,图中显示在刚性地面弹跳机构弹跳高度为2.0 m,而在硬黏土地面弹跳高度约1.4 m,在草地地面几乎无法起跳,弹跳高度约0.1 m。模拟脚在刚性地面弹跳脚下陷深度为0 mm,在硬黏土地面下陷深度约为12 mm,在草地地面下陷深度约为18 mm。
|
| 图 12 测试压力-时间曲线 Fig. 12 Pressure-time curves tested |

|
| 图 13 不同地面弹跳结果 Fig. 13 Hopping results on different grounds |
为简化计算,将气缸与弹跳腿之间滑动摩擦阻尼力视为恒值35 N,复位弹簧刚度为2 244 N/m,磁铁锁紧力大小随相对位移s之间变化规律为[7]
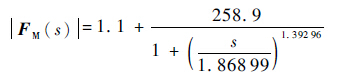 (13)
(13)
将刚性地面弹跳过程中测得的最大压力代入式(3)与式(7)、式(5)联立,求得气缸速度变化曲线。同理,在硬黏土地面与草地地面弹跳试验测得的最大压力代入式(3)与式(1)、式(2)联立,求得气缸与弹跳脚的位移、速度变化曲线。分析得到机器人在3种地面起跳过程中m1与弹跳脚的位移与速度随时间变化结果(见图 14)。

|
| 图 14 不同地面仿真结果 Fig. 14 Simulation results on different grounds |
由图 14(a)可以看出:机器人在刚性地面弹跳仿真得到m1碰撞前后的速度为6.9 m/s和6.22 m/s,根据式(6)计算得到其弹跳高度为1.97 m,图 14(b)显示当δ1+δ2=48 mm即m1与弹跳脚之间相对距离达到最大行程时刻弹跳脚的下陷位移为7 mm且处于静止状态,而该时刻m1的上升速度为6.2 m/s小于在刚性地面碰撞前的速度,其主要原因是燃烧室内气体对外做的功一部分转化成地面下陷的能量,同理根据计算得到机器人最终的起跳速度和弹跳高度分别为5.59 m/s和1.59 m。
从图 14(c)中可以看出:当机器人在草地土弹跳时仿真得到的脚下陷深度为25 mm,机器人最终起跳速度与弹跳高度分别为1.89 m/s和0.18 m,弹跳机构在较小的输入能量情况下,在草地土弹跳地面下陷深度大于在较大充气压力下硬黏土地面弹跳下陷深度,并且弹跳脚在起跳过程中最大速度大于在硬黏土地面弹跳结果,该结果表明地面特性直接影响了机器人的弹跳结果。
由图 14可以看出:仿真得到的机器人在3种地面的弹跳高度、脚下陷深度与试验结果相差较小,而出现偏差的主要原因是由地面的非均质性导致弹跳地点力学参数与所测参数存在偏差以及试验过程中的测量偏差导致的。
4 结 论1) 通过对燃气动力弹跳机器人工作过程分析,得到机器人起跳过程弹跳机器人动力学模型,并对弹跳脚与模拟地面的Hunt-Crossley接触力模型中参数进行拟合测试。
2) 将弹跳机构置于模拟地面中弹跳测试,当燃气驱动器充入0.01 MPa丙烷与0.21 MPa一氧化二氮时,弹跳机构在刚性地面、硬黏土地面弹跳高度分别约为2.0 m和1.4 m,表明不同地面对弹跳性能影响较大,在草地地面充气压力为0 MPa条件下,其弹跳高度为0.1 m,在刚性地面、硬黏土地面及草地地面3种力学特性地面仿真弹跳高度分别为1.97、1.59和0.18 m,下陷深度分别为0、7和25 mm,仿真与试验结果偏差较小,建立的动力学模型可用于燃气动力弹跳机器人在不同力学特性地面弹跳性能分析。
3) 本文针对刚性脚与不同力学特性地面垂直弹跳条件下进行分析,但当脚的形状及尺寸、起跳角度改变也会影响弹跳机器人脚与地面接触力大小,因此建立更完整的脚与地面接触模型是弹跳机器人以后研究的方向。
| [1] | 尹军茂, 陈殿生, 沈奇. 仿蝗虫跳跃机构设计与分析[J]. 北京航空航天大学学报,2013, 39 (10) : 1348 –1353. YIN J M, CHEN D S, SHEN Q. Design and analysis of locust-like jumping mechanism[J]. Journal of Beijing University of Aeronautics and Astronautics,2013, 39 (10) : 1348 –1353. (in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [2] | 柴辉, 葛文杰, 魏敦文, 等. 一种间歇式弹跳机器人的机构设计与跳跃性能分析[J]. 机械工程学报,2012, 48 (13) : 19 –26. CHAI H, GE W J, WEI D W, et al. Mechanism design and hopping performance analysis of an intermittent hopping robot[J]. Journal of Mechanical Engineering,2012, 48 (13) : 19 –26. (in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [3] | ZHAO J, XU J, GAO B, et al. MSU jumper:A single-motor-actuated miniature steerable jumping robot[J]. IEEE Transactions on Robotics,2013, 29 (3) : 602 –614. |
| Click to display the text | |
| [4] | KOVAĆ M, SCHLEGEL M, ZUFFEREY J C, et al. Steerable miniature jumping robot[J]. Autonomous Robots,2010, 28 (3) : 295 –306. |
| Click to display the text | |
| [5] | SCARFOGLIERO U,STEFANINI C,DARIO P.Design and development of the long-jumping[C]//IEEE International Conference on Robotics and Automation.Piscataway,NJ:IEEE Press,2007:467-472. |
| Click to display the text | |
| [6] | DUBOWSKY S, KESNER S, PLANTE J S, et al. Hopping mobility concept for search and rescue robots[J]. Industrial Robot,2008, 35 (3) : 238 –245. |
| Click to display the text | |
| [7] | NOH M, KIM S W, AN S, et al. Flea-inspired catapult mechanism for miniature jumping robots[J]. IEEE Transactions on Robotics,2012, 28 (5) : 1007 –1018. |
| Click to display the text | |
| [8] | WANG H M, LUAN Y G, OETOMO D, et al. Design, analysis and experimental evaluation of a gas-fuel-powered actuator for robotic hoppers[J]. IEEE/ASME Transactions on Mechatronics,2015, 20 (5) : 2264 –2275. |
| Click to display the text | |
| [9] | SALTON J R,BUERGER S,MARRON L,et al.Urban hopper[C]//SPIE Defense Security and Sensing International Society for Optics and Photonics.Bellingham:SPIE,2010:76920Z. |
| Click to display the text | |
| [10] | ACKERMAN E.Boston dynamics sand flea robot demonstrates astonishing jumping skills[EB/OL].IEEE Spectrum Robotics Blog(2012-03-28)[2015-06-03]. http://spectrum.ieee.org/automaton/robotics/military-robots/boston-dynamics-sand-flea-demonstrates-astonishing-jumping-skills/. |
| Click to display the text | |
| [11] | DING L, DENG Z, GAO H, et al. Planetary rovers' wheel-soil interaction mechanics:New challenges and applications for wheeled mobile robots[J]. Intelligent Service Robotics,2011, 4 (1) : 17 –38. |
| Click to display the text | |
| [12] | IRANI R A, BAUER R J, WARKENTIN A. A dynamic terramechanic model for small lightweight vehicles with rigid wheels and grousers operating in sandy soil[J]. Journal of Terramechanics,2011, 48 (4) : 307 –318. |
| Click to display the text | |
| [13] | LEVER J H, SHOOP S A, BERNHARD R I. Design of lightweight robots for over-snow mobility[J]. Journal of Terramechanics,2009, 46 (3) : 67 –74. |
| Click to display the text | |
| [14] | YEOMANS B, SAAJ C M, VAN WINNENDAEL M. Walking planetary rovers:Experimental analysis and modeling of leg thrust in loose granular soils[J]. Journal of Terramechanics,2013, 50 (2) : 107 –120. |
| Click to display the text | |
| [15] | 张克通.轮式移动弹跳机器人研究[D].南京:南京航空航天大学,2010:17. ZHANG K T.Research on wheeled hopping robot[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2010:17. (in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [16] | TILIAKOS N,TYLL J S,HERDY R,et al.Development and testing of a nitrous oxide/propane rocket engine:AIAA-2001-3258[R].Reston:AIAA,2001. |
| Click to display the text | |
| [17] | BEKKER M G. Land locomotion on the surface of planets[J]. ARS Journal,1962, 32 (11) : 1651 –1659. |
| Click to display the text | |
| [18] | HUNT K, CROSSLEY F. Coefficient of restitution initerpreted as damping in vibroimpact[J]. Journal of Applied Mechanics,1975, 42 (2) : 440 –445. |
| Click to display the text | |
| [19] | WONG J Y. Theory of ground vehicles[M]. Hoboken,NJ: John Wiley & Sons, 2008 : 65 . |
| Click to display the text | |
| [20] | DING L, GAO H, DENG Z, et al. Foot-terrain interaction mechanics for legged robots:Modeling and experimental validation[J]. The International Journal of Robotics Research,2013, 32 (13) : 1585 –1606. |
| Click to display the text | |





